基于FOA-BP神经网络的高铁沉降预测

陈 涛

(中国铁路设计集团有限公司，天津 300251)

BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，在高铁、建筑物沉降等方面有着广泛应用。张文博[1]基于BP神经网络预测了建筑物的沉降，厉东伟[2]将BP神经网络应用于高铁的沉降预测中，均取得了较好的效果。赵杰[3]采用ARIMA_BP组合模型预报高铁的沉降，刘建国[4]基于卡尔曼滤波的BP神经网络模型预测桥梁的形变，这两种模型均对原始数据进行了预处理，精度有所提高。吴伟立等[5]基于遗传算法优化BP神经网络，认为优化后的BP神经网络精度较传统BP算法高；林淼[6]利用粒子群算法优化BP神经网络，江丽[7]融合了粒子群算法与模拟退火算法对BP神经网络进行优化。从算法的复杂度考虑，遗传算法需要进行基因的选择、交叉和变异操作，粒子群算法需要对粒子最大速度、惯性权重、加速系数等多个参数进行调整，两种算法在预报的实现上较为复杂[8]。为了找到一种更为简单有效的方法，引入果蝇算法[9]对BP神经网络进行优化，通过与传统的BP神经网络进行对比，验证果蝇算法优化BP神经网络预测模型(FOA-BP)预测高铁沉降的可行性。

1 改进果蝇算法优化BP神经网络预测模型

1.1 改进的果蝇算法原理

果蝇算法基于果蝇的觅食演化来寻求全局最优。果蝇觅食的过程分为两步。第一步：依靠强大的嗅觉对食物源进行初步定位，快速飞近食物源；第二步：通过视觉找到并飞向食物源。因此，果蝇算法的基本寻优过程是：果蝇种群从给定的初始坐标出发，按照给定的飞行方向和飞行步距进行搜索(嗅觉搜索)，通过味道浓度初步确定与最优解的大致方向和距离，然后依靠视觉搜索到达最优解的位置[10]。由此可知，果蝇算法有迭代次数、种群规模、步长三个参数，对果蝇算法改进就是对其参数进行调整，以达到最佳优化效果。迭代次数能够满足模型收敛即可，过多的收敛步数并无意义。种群规模会对算法的精度产生影响，但同时也会显著降低算法的速度。

果蝇种群(包含N只果蝇)利用嗅觉搜寻食物的随机方向和距离，搜索方式为

xi=x0+t×rand，yi=y0+t×rand

(1)

其中i为(1，N)之间的整数，表示果蝇个体的数目；t为搜索步长；rand为(0，1)之间的随机数。

由当前最优的味道浓度判定值

(2)

得

(3)

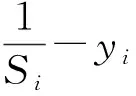
(4)

通过改进，可以根据上一步的步长对当前步长进行动态调整。一方面可以避免步长过大引起早熟收敛(局部最优)，另一方面也可以提高搜索速度，减少由于固定步长带来的收敛速度过慢的情况。由于公式(4)步长的符号为正，表示果蝇算法的搜索只能朝着一个方向，这仍然在一定程度上限制了果蝇算法的搜索能力。

1.2 改进果蝇算法优化BP神经网络预测模型的实现

将以上对果蝇算法的改进与BP神经网络进行融合，建立改进果蝇算法优化BP神经网络预测模型(以下简称FOA-BP神经网络算法)，用果蝇算法的味道浓度判定函数来替代BP神经网络中的基函数，通过迭代寻优，找到最适合的权值与阈值，然后代入BP神经网络中进行预测，实现步骤如下。

(1)初始化BP神经网络。根据网络的输入输出数据确定输入层、隐含层和输出层的节点数(分别为a，h，b)。同时，将样本的输入输出数据归一化，初始化输入层、隐含层和输出层之间的连接权值，初始化隐含层和输出层的阈值。

(2)初始化果蝇种群的位置、迭代次数、种群规模，将果蝇个体看作是BP神经网络中的连接权值及对应的阈值，给定随机方向和距离进行搜索。

(3)计算果蝇个体与原点的距离，再计算味道浓度判定值，味道浓度判定值为距离的倒数。

(4)将味道浓度判定值代入味道浓度函数，味道浓度函数为预测输出yi和期望输出y差值的平方求和，使其取极小值，即

(5)

(5)不断迭代，同时更新神经网络的权值与阈值，当味道浓度函数值满足要求或者达到迭代次数上限，即得到优化后的BP神经网络权值和阈值。

(6)利用优化后的权值和阈值构建BP神经网络，对目标数据进行预测。

(7)采用以下两个评价指标对两种算法的预测沉降量进行对比分析。

①均方误差MSE[11]：是观测值与真值偏差的平方和与观测次数比值的平方根，用于衡量观测值和真值之间的偏差，公式为

(6)

②平均相对百分比误差MAPE[12]，可以用来衡量一个模型精度的高低，其值越小说明模型精度越高，其公式为

(7)

2 实例分析

以河北省某地区高速铁路为例，该地区属于华北平原，地势平坦，地层自上而下主要为第四系松散层、粉质黏土、粉土、粉砂及其互层[13]，地下水位深6.0～10.0 m，地下水对混凝土结构不具有侵蚀性。高铁路基采用CFG桩网复合地基[14]，设计单桩承载力为400 kN。桩顶设0.6 m厚的碎石垫层，其上填筑高度为8.0 m的路基。已进行超载预压，实际堆载预压期为13个月，纵剖面如图1所示。沿既有高铁轨道线间及两侧路肩每隔约20 m布置一个沉降监测点，平面位置如图2。

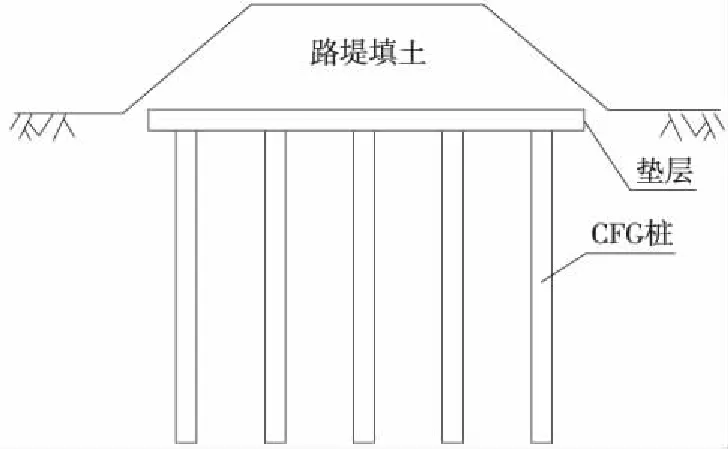
图1 高铁路基纵剖面

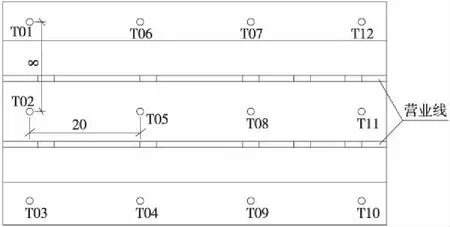
图2 监测点平面位置(单位：m)

按照二等水准测量精度要求，采用Leica DNA03型电子水准仪及配套的设备对路基监测点进行观测。为提高观测数据的准确性，每次监测实行“三固定”，即“固定测量人员、固定测量仪器、固定观测路线和方法”[15]。选取T01监测点作为沉降预测的对象，自2017年3月16日至2018年1月16日进行了20次观测(每半月进行一次监测)，原始累计沉降数据如表所1示。

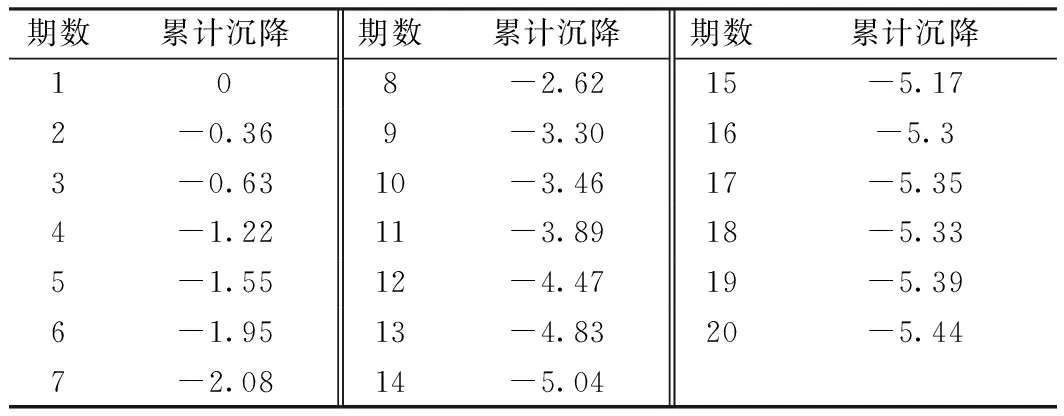
表1 T01原始累计沉降量 mm

为了验证FOA-BP神经网络在高铁沉降预测中的可行性，以表1中前15期观测数据为样本，分别采用BP神经网络和FOA-BP神经网络进行训练，采用由前3期观测数据预测后1期数据的滚动组合方式对后5期沉降数据进行预测，选取输入层节点数a=3，输出层节点数b=1，经过试验得到最为合适的隐含层节点数h=7。

通过试验数据对比分析，得到两种算法的预测沉降数据及其残差，如表2所示，两种算法的预测累计沉降量对比如图3。

由图3可知，两种算法均可以较好地反映T01监测点的沉降趋势，其中BP神经网络在个别监测周期的预测值与实测值差别很小，但是就整体而言，BP神经网络只能反映出沉降的趋势，不能准确预测累计沉降。从表2可知，BP神经网络均方误差为0.021，经优化后为0.009，说明FOA-BP神经网络预测沉降值与实测沉降值差距较小。BP神经网络平均相对误差为0.828%，优化后平均相对百分比误差显著降低，预测精度得到了提升。由此得出，FOA-BP神经网络算法预测精度更高。此外，在同样的约束条件下，FOA-BP神经网络在4步实现收敛，而BP神经网络需要34步，故FOA-BP神经网络算法的预测速度更快。

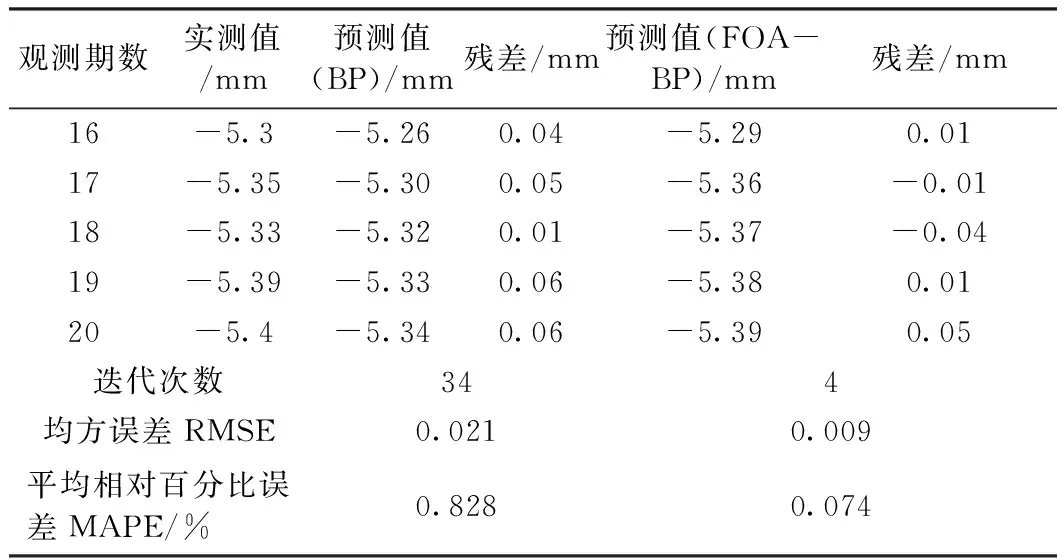
表2 两种算法的预测沉降数据及其残差对比

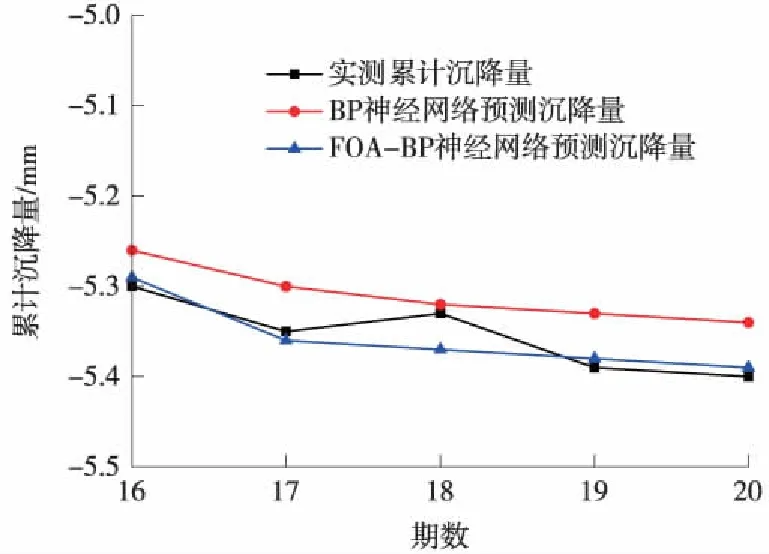
图3 两种算法的预测沉降数据对比

为了避免监测点选取的偶然性，另外随机选取监测点T11进行预测。T11的原始累计沉降量如表3所示，两种算法的预测沉降数据及残差如表4所示，两种算法的预测结果对比如图4。

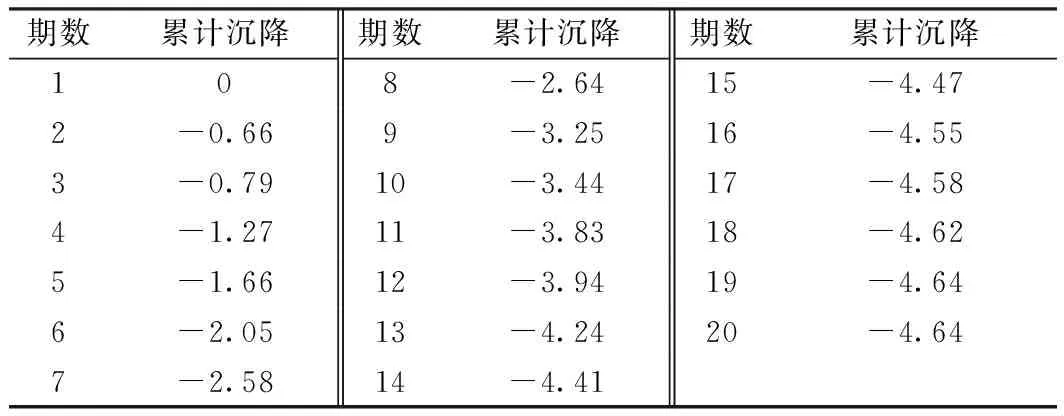
表3 T11原始累计沉降量 mm

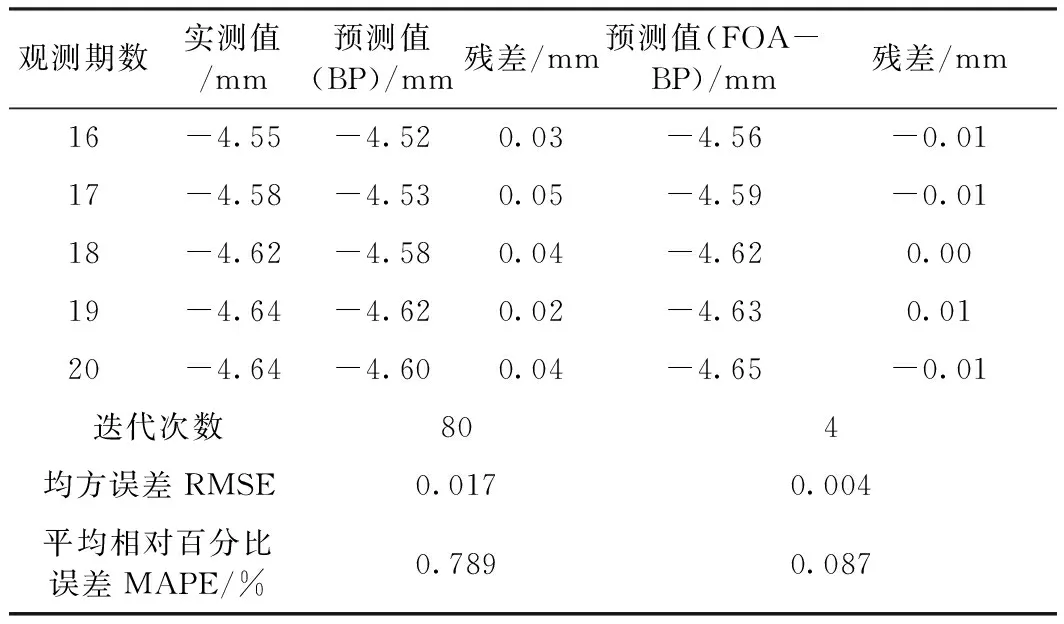
表4 两种算法的预测沉降数据及其残差对比

图4 T11监测点两种算法的预测沉降数据对比

由图4可知，FOA-BP神经网络较BP神经网络更为准确地预测了T11号监测点的沉降趋势。由表3和表4中可得， FOA-BP神经网络在迭代次数、均方误差和平均相对百分比误差等方面均远小于BP神经网络。

3 结束语

(1)与BP神经网络相比，FOA-BP神经网络降低了均方误差，提高了模型精度，预测精度更高。在使用时，需要提前剔除异常值，避免对预测结果产生干扰。

(2)迭代次数和种群规模对果蝇算法的优化影响不大，步长是影响果蝇算法优化精度的主要参数，步长的动态调整可以避免早熟收敛或者收敛速度过慢的情况。

(3)FOA-BP神经网络具有预测精度高、预测速度快的优点，但是也存在着一些不足(果蝇算法只能单向搜索)，在以后的研究中还需要对果蝇算法做进一步的改进。