冬枣辅助采摘车车架结构优化设计——基于层次分析法

刘广新，王淑君，赵玉刚，蔡善儒

(山东理工大学a.机械工程学院；b.农业工程与食品科学学院 ，山东 淄博 255049)

0 引言

沾化冬枣味道甘甜，皮薄肉脆，种植于山东、陕西等地。冬枣的产量逐年增加，到2020年产值可达40亿元。但是，在其采摘过程缺少机械化，出现了采摘效率低、劳动量大、劳动力短缺等问题。为此，设计了一款适合冬枣种植情况的冬枣采摘车。该车的主要工作环境是野外枣园，地面松软且凹凸不平，受力情况较普通车辆复杂。若车架质量过大,会影响整车的动力配置，提高整车研究成本；同时，会造成冗余材料的浪费，不能发挥材料的最大性能，影响整车续航时间。因此，性能良好的车架成为保证辅助人工采摘车工作性能的关键环节。

冬枣辅助人工采摘车车架的结构设计在现阶段主要依靠经传统经验设计，而这类方法一般通过增加各组件的厚度来解决强度问题，但随之而来的是车架质量过大，造成材料的浪费。近年来，专家学者纷纷借助CAD/CAE软件来获得最优机械性能。周方思[1]等根据有限元静力学分析结果，结合拓扑优化的方法对除草机车架进行减重优化。毛鹏军[2]等在研制的烟田辅助采收机的基础上，使用ANSYS Workbench对车架进行有限元分析，根据分析结果做了轻量化设计。上述研究方法，通常根据材料的最大屈服强度，通过减少材料达到减轻质量的目标，但动态性能却没有得到提升。本文在有限元静动力学分析的基础上，结合灵敏度分析方法与层次分析法的各自特点对车架结构进行多目标优化设计，并进行优化前后结果比较。结果表明：使用灵敏度分析法与层次分析法相结合，对车架多目标优化是可靠与合理的。

1 车架有限元静动力学分析

为了得到车架模型的最大变形量和低阶固有频率，需要对车架模型进行有限元静动力学分析[3]。

1.1 车架有限元建模

根据车架实际尺寸大小，在Pro/E软件中建立车架参数化模型。其中，车架全长1.950m，宽0.96m，高0.27m。车架各部件均由不同厚度的矩形钢管焊接而成，材料为易于焊接的Q235，质量为132.65kg。车架简化模型和部件编号如图1 所示。

为了提高有限元分析的准确性和缩短计算时间，一般要对对车架模型中小的倒角、圆角、孔等特征进行相应的简化[4]。将建立好的车架模型通过软件间的友好链接通道导入AWB中，以免丢失数据和模型特征。在AWB中选择SOLID187单元划分四面体单元，尺寸设置为20mm，划分网格后生成节点数129 607个，单元数66 168个，划分网格后的模型如图2所示。

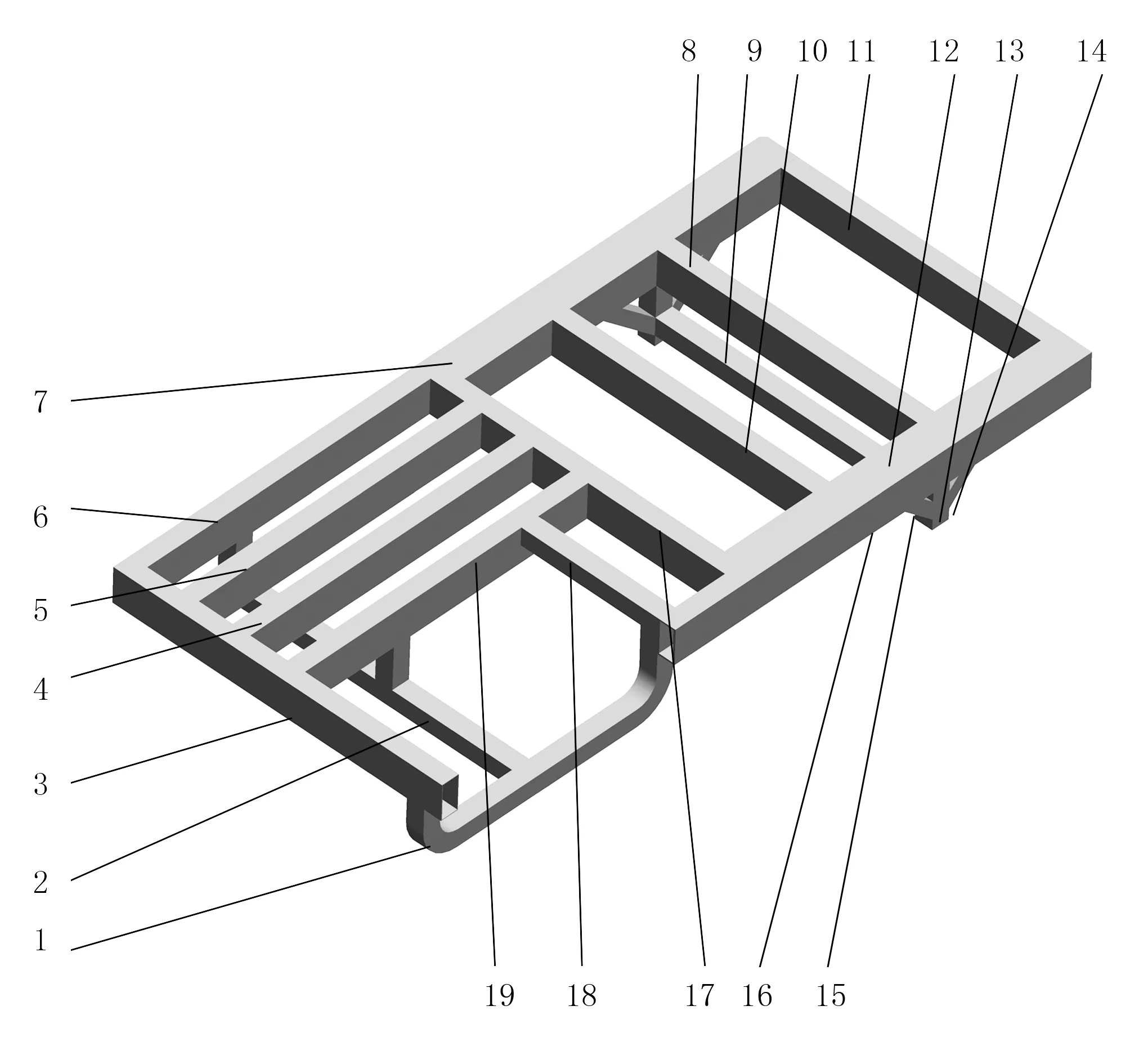
1.驾驶室U型梁 2.前轮轴固定梁 3.前防撞梁 4.前作业单元副支撑梁 5.前抗扭组件 6.左主纵梁 7.左副纵梁 8.后作业单元支撑主梁 9.后轮轴固定梁 10.后作业的单元支撑副梁 11.后防撞梁 12.右副纵梁 13. 后轮轴支撑柱 14.后轮轴支撑住后斜支撑 15.后轮轴支撑住前斜支撑 16.右主纵梁 17.中间防扭组 18.座椅支撑梁 19.前作业单元主支撑梁

图2 车架有限元模型

1.2 车架模型合理性实验验证

合理、准确的车架模型能够为车架结构优化提供准确的数据。为此，设计了车架模型合理性验证实验，测量了停放于水平地面的车架不同位置的应力，具体测量点分布位置如图3所示。整车空载时布置测量点，满载时加载的质量主要是驾驶员(68.2kg)、前作业单元作业者(66.1kg)、后作业单元作业者(70.2kg),载荷稳定后测量[5]。实验设备：德国IMC公司研制的IMCCL-5016应变测试系统、BX120-2AA应变片、电动角磨机、101胶水、砂纸、FAMOS软件及体重秤等。

图3 车架应力测量点散布图

由表1中应力测量值与仿真值对比可知：除 1处和7处的测量数据与仿真数据相对误差较大外，其它点的误差均在15%以内，误差均在许可范围内，所建立参数化模型准确合理。

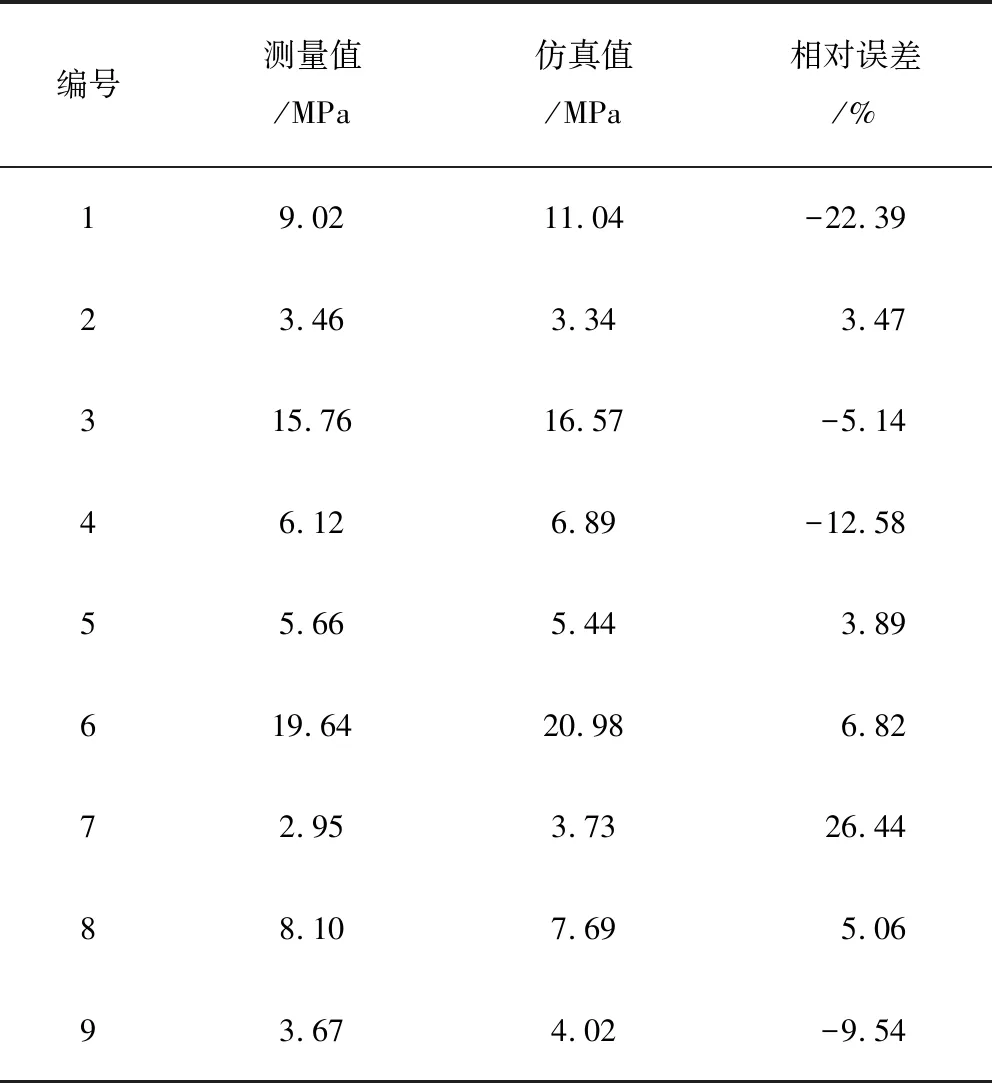
表1 应力测量值与仿真值

1.3 车架极限工况下静力学分析

结合车架实际工作状态对车架模型做有限元分析，能够提供合理、有效的优化数据。为此，选取车架极限静止状态对车架模型进行有限元分析。车架极限状态下，右前轮和左后轮轴固定处的约束为位移约束。冬枣辅助采摘车车架用于承载采摘作业单元与采摘作业人员(4 000N)、蓄电池组(3 400N)、液压站(300N)、电动机、驾驶室和驾驶员(1 000N)等。其中，采摘作业人员和驾驶员体重均按70kg计算，电动机固定在后轮轴上质量不计。车架选用不同规格的矩形管焊接而成，材料均选用易于焊接的Q235。各部分均等效为集中载荷施加到对应位置，车架的自重通过材料属性设置自动添加[5]。经AWB求解后的应力分布图和总变形分布图如图4、图5所示。

图5 总变形分布图

由图4可以看出：车架的最大应力出现在左后轮轴固定处，为117.43MPa，远小于车架的最大屈服极限强度235MPa，满足车架强度设计要求，还有较大的设计余量。由图5可以看出：车架的最大变形出现在右主纵梁与后防撞梁链接处，为1.804 5mm，远小于车架最大变形量参考值。结合以上分析，在保证车架静态极限工况下的性能下，可以对车架进行轻量化优化设计。

1.4 车架模态分析

模态分析是动力学分析的关键，车架的模态分析直接反映了车架结构动力学特性[6]。 在车架的模态分析中，各阶模态所占有的权重随模态频率的增加而降低。在AWB中车架进行模态分析时，边界条件为自由边界，设置频率最小为1Hz，最大为250Hz。由自由模态分析得到前4阶模态如图6～图9 所示，对前4阶振型进行描述如表2所示。

图6 车架第7阶模态云图

图7 车架第8阶模态云图

图8 车架第9阶模态云图

图9 车架第10阶模态云图

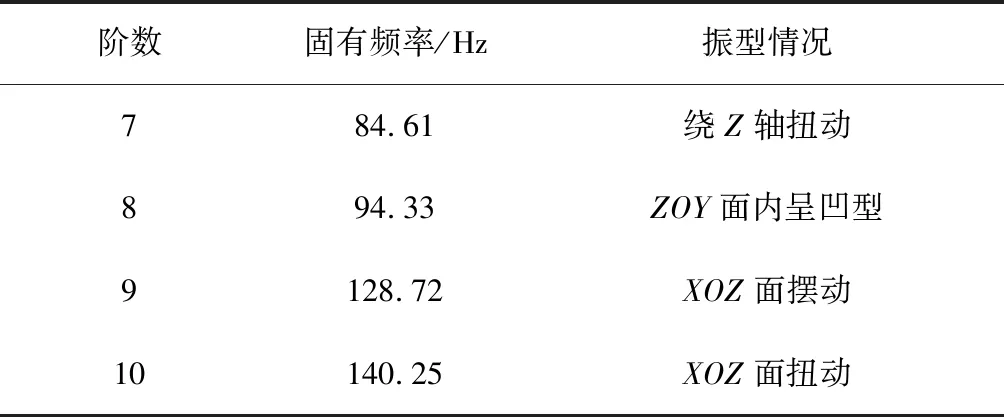
阶数固有频率/Hz振型情况784.61绕Z轴扭动894.33ZOY面内呈凹型9128.72XOZ面摆动10140.25XOZ面扭动

冬枣辅助采摘车车架的激励主要由路面和电动机产生，其中路面激励频率不大于3Hz。冬枣辅助采摘车属于微型电动车，车速最大40km/h时，发动机振动频率可达80Hz，非常接近车架低阶固有频率，共振情况容易发生，影响车架性能[7]。因此，车架低阶固有频率需要提高。通过对车架前4阶振型结果分析可知：车架各部件动刚度存在不足，需要对其进行优化设计。

2 车架参数灵敏度分析

灵敏度分析法可借助特定的数学方法计算出结构的性能参数随设计变量变化的灵敏度，然后结合结构整体性能要求，合理、有效地选择需要优化设计的部分[8]。该方法可以有效地找出对车架性能影响大小的设计变量,提高车架优化效率[9]。考虑到对车架整体性能的影响，选取了车架19个主要部件(见图1)的厚度作为设计变量，将质量、低阶频率、总变形量作为影响车架性能的指标。利用AWB求解出19个设计变量对车架动静态性能影响的灵敏度数据经过处理得到如图10～图12所示的质量、低阶频率、最大应力灵敏度分析图。

图10 质量灵敏度分析图

图11 低阶频率灵敏度分析图

图12 最大应力数灵敏度分析图

其中，条形图的长度表示参数对指标的影响程度，长度越长影响越大。零刻线以上的呈正相关，表示指标随着设计变量的增加而增加，或指标随着设计变量的减少而减少；反之，零刻线以下的呈负相关，表示指标随着设计变量的增加而减少或指标随着设计变量的减少而增加。

通过分析图10～图12可知：在19个设计变量中，编号2、4、5、14、15、18的部件厚度对3个指标的影响都很小，可以作为非关键设计变量，保留设计厚度不变，其余设计变量均作为关键设计变量。

3 车架数学模型建立与求解

车架轻量化设计不仅可以增加整车的续航时间，而且可以提高车架材料的使用率，减少材料与能源的浪费。车架的固有频率提高可以有效地避开共振频率，提高车架的动刚度。结合有限元静动力学分析结果和灵敏度分析结果，将车架的质量和低阶固有频率作为优化目标。由于质量减少的同时车架的最大应力和最大变形也会随之增加，这样就会使车架轻量化设计失去意义，故限制极限工况下安全系数为1.5。结合灵敏度分析结果，以车架各组件的厚度作为设计变量，其中驾驶室U型梁x1，前防撞梁x3和后轮轴支撑柱x13下限2mm、上限4mm；左主纵梁x6，左副纵梁x7，后作业单元支撑主梁x8，后轮轴固定梁x9，后作业的单元支撑副梁x10，右副纵梁x12，右主纵梁x16，中间防扭组件x17和前作业单元主支撑梁x19的下限均为2mm、上限均为8mm；后防撞梁x11的下限为1mm、上限为3mm；其余部件厚度保持不变。在冬枣辅助采摘车车架模型中，车架质量、车架低阶固有频率、车架最大应力作为目标函数，定义19个变量，根据灵敏度分析结果选取13个变量作为设计参数组合(X)=g(x1,x3,x6,…,x13,x16,x17,x19)。车架结构优化设计数学模型为

将车架各组件厚度尺寸作为变量，代入上述数学模型反复迭代后求解得到5组车架设计方案非劣解，如表3所示，各方案对应的变量参数如表4所示。

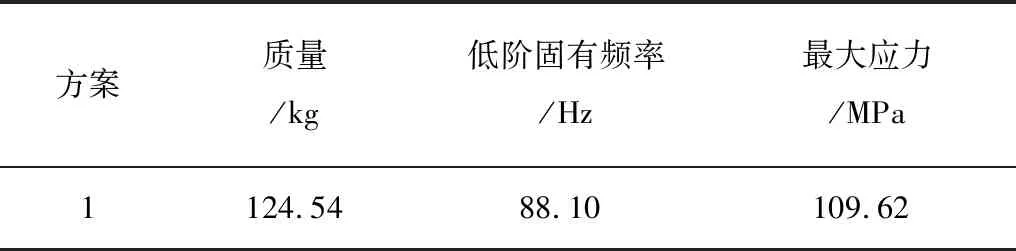
表3 5组车架设计方案

续表3

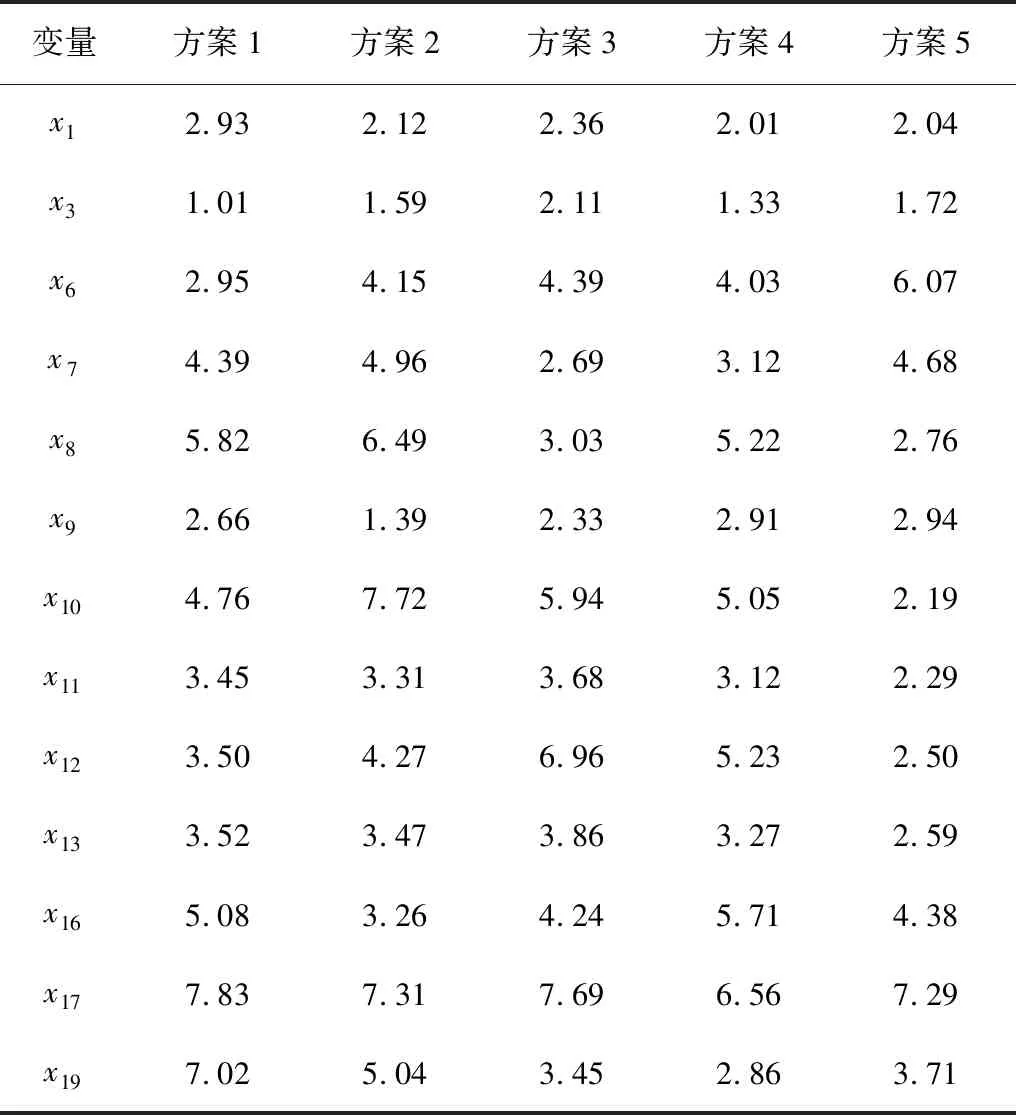
表4 车架设计方案变量参数

4 层次分析法优化车架性能

车架的优化设计方案需要借助一定的评价方法来获取最优设计。层次分析法是一种有效结合定性分析与定量分析的决策方法，能够对一些较为复杂、模糊的问题做出简便、灵活的决策[10]。其基本思想是：通过将复杂问题分解，按照支配关系形成递阶层结构，同时根据一定的比率标度，通过两两比较将判断定量化，最终得到最优方案[11]。

4.1 层次结构模型建立

层次分析法模型分为3层，依次为目标层、准则层、方案层。其中，目标层为冬枣辅助采摘车车架的最优设计方案；准则层为车架的最大应力、车架的质量及车架的固有频率。目标层由1个元素组成，准则层与方案层由多个元素组成，同一层的每个元素对上一层的影响不同。车架设计方案层次结构模型如图13所示。

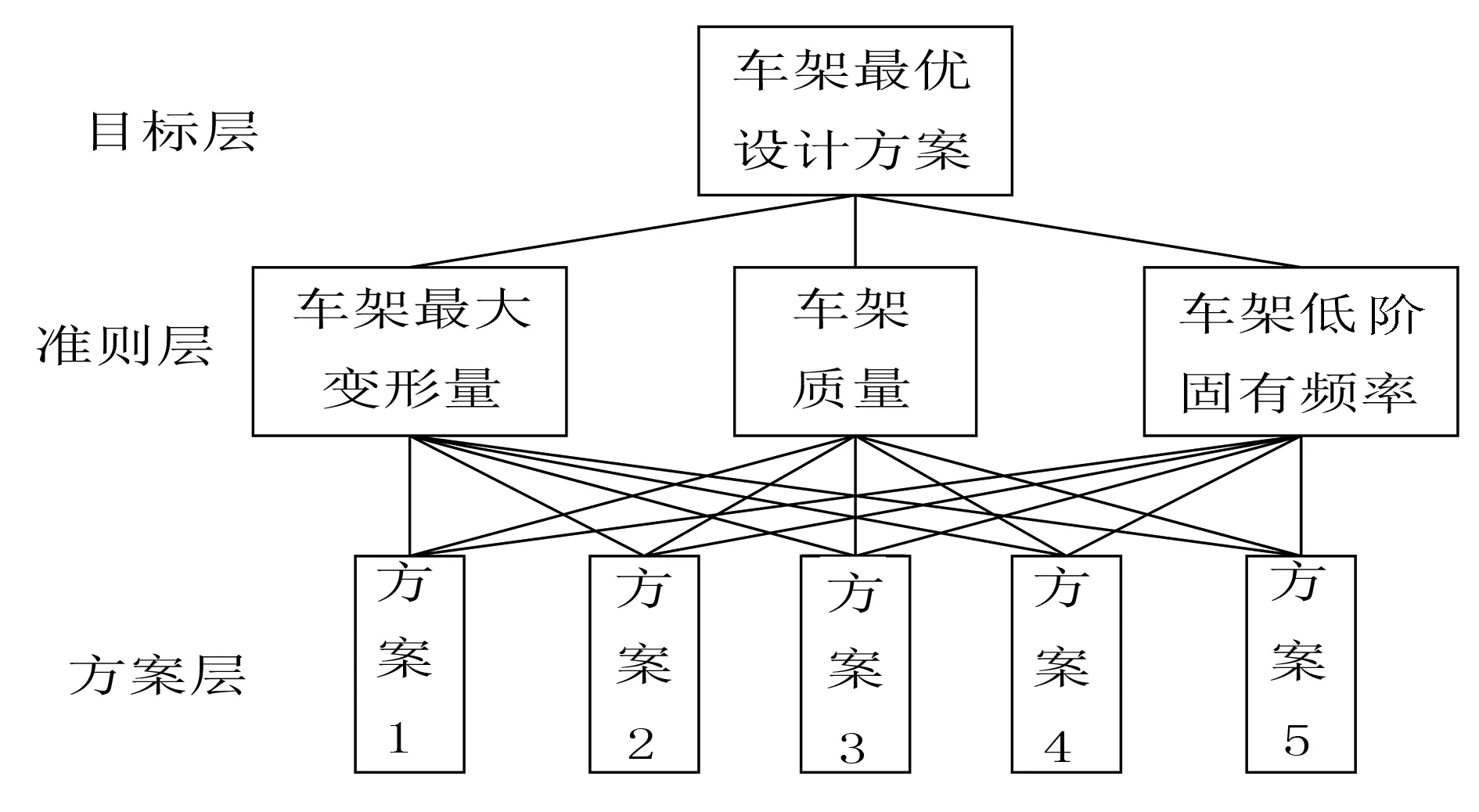
图13 车架设计方案层次结构模型

4.2 优先级矩阵建立

在保证车架的强度和刚度前提下，车架的质量应当越小越好，也就是说车架质量的倒数越大越好。根据以上分析得到5种设计方案的质量倒数矩阵，即

Nm=(0.00803 0.00779 0.00777 0.00811

0.00798)

将得到车架的质量倒数矩阵中各元素进行比较，具体参见文献[12]，得到矩阵为

Wm=

将矩阵Wm各列元素相加得到矩阵为

Qm=(0.94146 5.09371 5.10682 4.89271

4.97243)

将矩阵Wm各列元素分别除以矩阵Qm中对应列的元素所得的商相加再求平均值，得到的矩阵则为5种方案中车架质量优先级矩阵，即

Pm=(0.20237 0.19632 0.19582 0.20439

0.20111)

同理，则可以得到车架低阶频率和车架最大应力对应的优先级矩阵为

Pf=(0.20152 0.20257 0.20099 0.19774 0.19717)Pσ=0.19111 0.20537 0.20956 0.19258 0.20138)

4.3 判断矩阵构建立

在层次分析法中，判断矩阵常常采用Thomas L. Saaty提出的“1-9”标度法来建立。“1-9”标度法主要用于对相对重要性的数值表示，从而构建判断矩阵[13]，如表5所示。在车架机构优化过程中，车架质量的降低可以有效地降低整车能耗，故车架质量比车架低阶频率和车架最大应力稍微重要。车架的低阶频率也会直接影响整车的动态性能，相比较而言车架最大应力稍微重要。根据以上分析，可以确定判断矩阵I，即

由矩阵I求得λmax= 3.0536，一致性检验得CI=0.0268<0.1，通过一致性检验。

根据公式(2)，有

AT=λmaxAT

(2)

其中，A为判断矩阵，λmax为矩阵A的最大特征值。计算出权重矩阵A，即

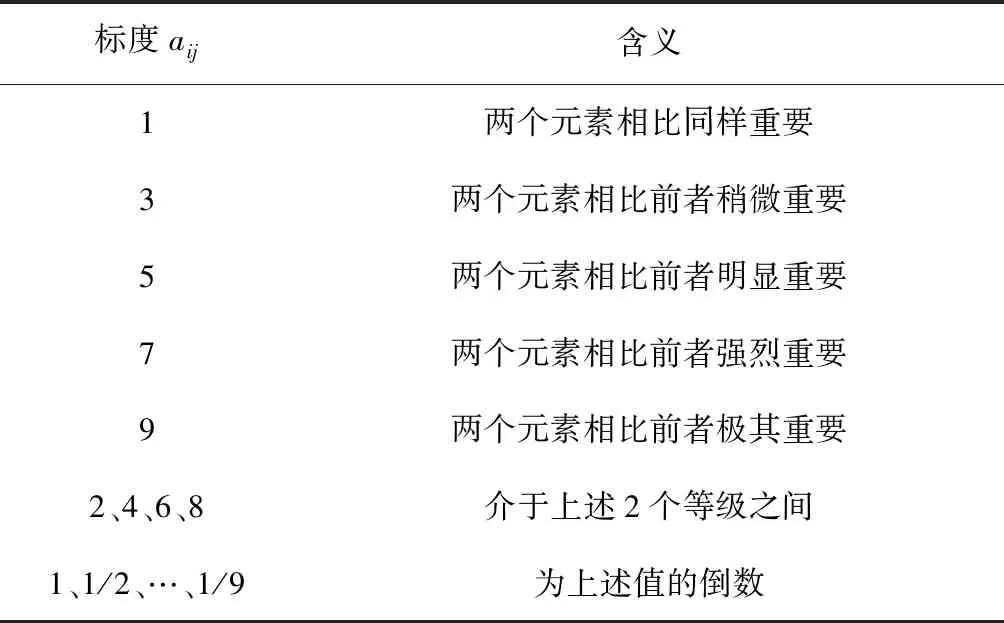
表5 因素重要度对比

4.4 最优解的确定

5种方案对应的各评判标准的优先级矩阵组成,矩阵P、矩阵A左乘矩阵P得到5个方案对应的量化指标为

AP=(0.20052 0.20029 0.19926 0.20080

0.20002)

根据上述计算结果，可以得出冬枣辅助采摘车车架结构优化设计方案优劣顺序为：方案4、方案1、方案2、方案5、方案3。以上5种方案均优于原方案，且方案4为最优设计方案。车架优化后各参数对比如表6所示。

表6 车架优化前后各参数对比

其中，较优化前车架总质量降低 7.01%，低阶频率提高2.17%，最大应力降低7.32%，动静态性能都有所提高。车架优化后，冬枣辅助采摘车样机的装配过程中效果良好，整车性能得到提升。图14为冬枣辅助采摘车样车。

图14 冬枣辅助采摘车

5 结论

将多目标优化应用到冬枣辅助采摘车车架的性能优化中，建立了以车架质量、最大应力和低阶固有频率为优化目标函数的数学模型，优化了车架多个性能参数。采用层次分析法优化后，较优化前车架总质量降低 7.01%，低阶频率提高2.17%，最大应力降低7.32%，应力较优化前均匀分布，整车动静性能均有提高。