向量在高中数学解题中的应用

□甘肃省金昌市永昌县第一高级中学 徐有彪

向量是高中数学课程的重要教学内容，也是高中数学解决问题的常用工具。向量最早出现于物理学中，多用来表示速度、位移、力等，英国科学家牛顿首次将向量和有向线段联系起来，为向量的数学应用铺平了道路。18世纪末，挪威数学家威赛尔通过坐标平面上的点来表示复数a＋bi，并借助具有几何意义的复数运算来定义向量运算，向量正式进入数学领域。在高中数学教学中，教师要重视向量的解题应用，以此作为提升学生解题能力的有效方式。

一、数列问题中的解题应用

数列是高中数学的主干知识，也是考试命题的重要内容。高考试卷多以数列作为压轴题，且数列知识点较多，学生在解题中容易出现误区，犯错率较高。虽然平面向量与数列之间的知识联系较少，但命题者有时将数列的性质与向量共线的条件结合起来，这就需要学生在解题中利用向量的共线定理来解决问题。举例而言，Sn为数列{an}的和，现在已知an-an＋1=d（d∈R），其果A、B、C三个点处在同一条直线上，且不过O（0，0），那么S200等于多少？本道题表面上是数列求和问题，本质上考查的却是学生对向量共线定理的掌握情况。学生在解答问题中只要意识到向量定理在本题中的应用价值，接下来的计算难度将大为下降。根据向量共线基本定理，学生可以很快求出数列首项以及末项的和，然后再借助数列的求和公式，快速地得出问题答案，简单明了，且不易出现计算错误。

二、三角函数中的解题应用

三角函数是高中数学解题的常见内容，三角函数的解题方法比较多元，最为常见的便是运用各种公式进行代数运算。三角函数在命题中常渗透平面向量的内容，比如平面向量的数量积、坐标运算以及向量的共性及垂直的条件，使问题的呈现更具新颖性、综合性。这就要求学生在解题中能够从向量知识出发。举例而不仅考查向量的有关概念及运算，更考查向量与其他知识的综合应用，学生需要借助向量的坐标运算转化

三、平面几何中的解题应用

向量具有数形结合的特点，借助向量，不仅可以将枯燥抽象的代数问题转变为直观清晰的几何图形，也能将几何问题中的烦琐求证转变为相对简单的代数计算，从而实现化繁为简的目标。就以平面几何解题为例，不少平面几何问题难以借助常规的解法求出，此时，教师可以引导学生尝试着从向量的角度切入，将平面几何问题转化为向量问题，然后再利用向量的基本运算求解，降低题目的复杂性以及解题难度。举例而言，已知某△ABC，其中AM：AB=1：3，AN：AC=1：4，CN和BN相交于点E，若AB=m，AC=n，且∠BAC=60°，请求出AE的长度。本题涉及的知识点相对较多，传统的解题方法不仅烦琐，而且极易出错，教师可以借助向量来帮助学生转变思路，从而提高解题效率。比如先fffffd问题便迎刃而解。

四、立体几何中的解题应用

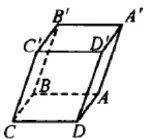
立体几何是高中数学教学的重要内容，也是学生学习难度比较大的内容。相比于平面几何、解析几何而言，立体结合对学生的空间思维能力有着更高的要求，学生在解题中，比如证明题中，经常容易出错。立体几何解题的常规思路为问题转化，即将立体几何的内容转化为更为熟悉的平面几何内容，然后再借助平面几何的知识来解决立体几何的问题。事实上，学生在解题中大都遵循此一思路。但在实际的解题中，部分问题即便转化后仍然比较复杂，此时，向量成为突破解题窠臼的有效方法。举例而言，某平行六面体ABCD-A′B′C′D′的 地 面 为 菱 形ABCD，且 ∠C′CB=∠C′CD=∠BCD=60°，求证C′C与BD垂直。传统的证明方式较为烦琐，需要借助线面垂直来推导线线垂直，而利用向量知识可以简化问题，比如然后利用向量的基本法则可以很快推导

五、结语

向量作为高中数学的重要知识点，是学生数学解题的利器。高中数学中的向量兼有代数形式和几何形式双重特征，学生利用其代数形式来解决几何问题，不仅可以提高学生的解题效率，在帮助学生串联数学知识点中也有很好的效果。