“2+26”城市空气质量综合评价比较研究

孙礼娜 汪凯 孙伟娜

(1. 安徽财经大学统计与应用数学学院， 安徽 蚌埠 233030； 2. 安徽农业大学生命科学学院， 合肥 230036)

近年来，京津冀及周边地区秋冬重污染天气频发，空气质量问题备受关注。如何有效防治大气污染，成为当前重要的研究课题之一。孙晓玲等人采用模糊综合评价和因子分析法对北京、天津、石家庄等 31个主要城市的空气质量进行了分析[1]。湛社霞等人利用灰色关联度法对粤港澳大湾区空气质量的影响因素进行了分析[2]。姚清晨采用小波分析等方法对太原市的空气质量变化特征进行了分析和预测[3]。孙爽等人对京津冀大气污染变化规律及其与植被指数的相关性进行了分析[4]。李颖若等人利用多元线性回归方法，定量评估了气象条件和空气污染控制措施对北京空气质量的影响[5]。

原国家环保部(现国家生态环境部)制定的《京津冀及周边地区2017年大气污染防治工作方案》中，将北京、天津及其他26个城市作为污染防治实施范围通道，简称“2+26”城市。本次研究中，将对“2+26”城市的空气质量进行综合评价。在其他研究的基础上，选取这些城市在2017年10月至2018年3月的AQI及w(PM2.5)、w(PM10)、w(SO2)、w(CO)、w(NO2)、w(O3)(月平均数据)[6-10]，分别用熵值法和因子分析法进行评价。根据评价结果，比较两种方法下“2+26”城市空气质量的排名情况，为治理环境污染、提升空气质量提供理论依据。

1 基于熵值法的“2+26”城市空气质量评价

借鉴相关文献[11-12]，结合“2+26”城市2017年10月至2018年3月的空气质量月平均数据，选取AQI及w(PM2.5)、w(PM10)、w(SO2)、w(CO)、w(NO2)、w(O3)作为评价指标。收集、整理这7个指标的相关数据，应用Matlab、Excel软件，采用熵值法计算各个评价指标的权重。表1所示为采用熵值法计算所得各指标权重。

7个指标权重之间的极差为0.089 2，同时指标所占权重均在0.100 0～0.200 0。由此可知，这7个指标对“2+26”城市的空气质量影响程度差别不大。其中，w(PM10)所占权重为0.191 5，对城市空气质量的影响最大；w(SO2)所占权重为0.102 3，其对城市空气质量的影响最小；w(CO)、w(NO2)和w(O3)所占权重非常相近，分别为0.156 0、0.154 2和0.156 5，极差仅为0.002 3，三者对空气质量的影响程度相近。运用综合指数模型公式，计算得出“2+26”城市空气质量综合得分，并据此对各城市空气质量进行排名。表2所示为采用熵值法所得“2+26”城市空气质量评价结果。

表2 采用熵值法所得“2+26”城市空气质量评价结果

以上评价结果反映了“2+26”城市某个时间段的空气质量得分和排名情况。其中，空气质量较好的5个城市分别为北京、廊坊、天津、开封和滨州，空气质量排名靠后的5个城市分别为安阳、晋城、石家庄、邯郸和邢台。

2 基于因子分析的“2+26”城市空气质量评价

首先，将7个指标作为原有变量对其进行检验，根据检验结果判断原有变量是否适合进行因子分析；然后，应用SPSS软件计算原有7个变量的相关系数矩阵[13-14]，以及Bartlett球形检验统计量的观测值和KMO值，根据检验结果进行分析。表3所示为原有变量的相关性矩阵。表4所示为KMO 和巴特利特检验结果。

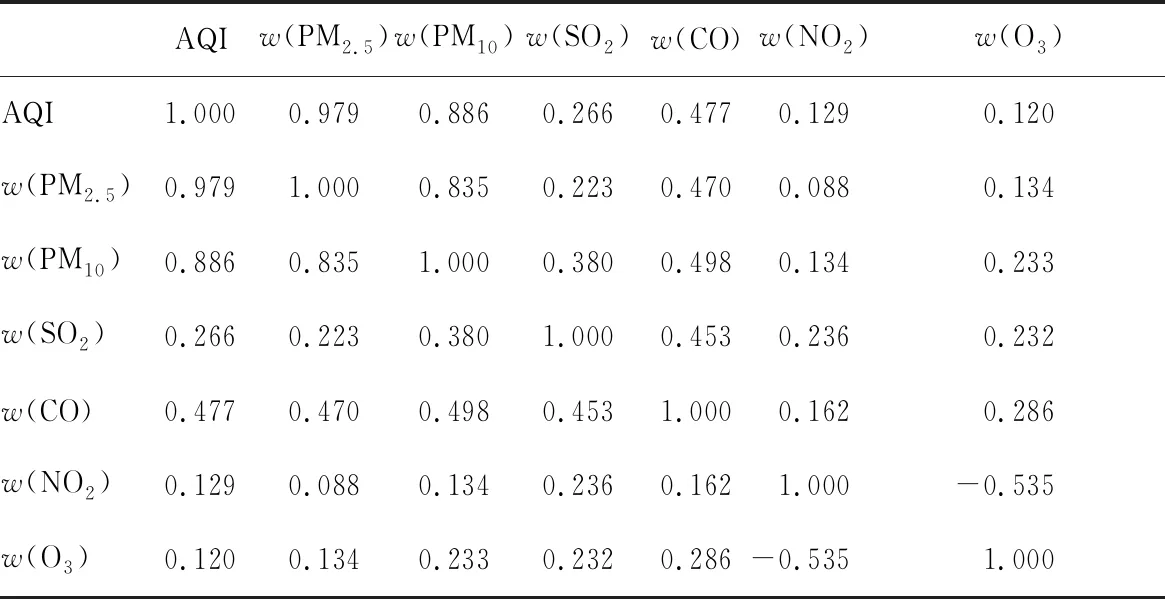
表3 原有变量的相关性矩阵

表4 KMO 和巴特利特检验结果

由表3可知，大部分变量之间的相关系数都比较高。由表4可知，KMO值大于0.6，为0.651，Bartlett球形检验统计量观测值为150.104，相应的概率接近0。这说明能够从原有变量中提取公共因子，即原有变量适合进行因子分析。对变量数据进行因子分析，输出结果如表5所示。

由表5可知，3个成分的初始特征值均大于1，且特征值分别为3.396、1.538和1.102；3个指标的累计方差贡献率为86.221%，大于80%。总体上看，原有7个变量的信息丢失较少，因子分析效果比较理想。

表5 因子解释原有变量总方差的情况

为了使公因子的实际意义得到准确解释，建立了因子成分矩阵(见表6)；接着应用SPSS软件，利用方差最大化正交旋转的方式，对公因子进行处理，得到因子载荷矩阵中方差最大的旋转矩阵(见表7)。

表6 成分矩阵

表7 旋转后的成分矩阵

由表7可知,AQI、w(PM2.5)、w(PM10)在第1个因子上有较高的载荷，w(SO2)和w(CO)在第2个因子上有较高的载荷，w(NO2)和w(O3)在第3个因子上有较高的载荷。

采用回归法估计出因子得分系数，并代入指标数据求得各城市空气质量的综合得分。选取的因子均为成本型数据，在对数据进行标准化处理时已经将成本型数据全部转化为效益型数据类型。综合得分数值越大，说明该城市的空气质量越好，空气质量排名越靠前；综合得分数值越小，说明该城市的空气质量越差，空气质量排名越靠后。表8所示为采用因子分析法所得“2+26”城市空气质量综合得分及排名。

采用因子分析法对“2+26”城市空气质量进行了评价，结果显示质量较好的5个城市分别为北京、廊坊、天津、郑州和鹤壁；空气质量最差的5个城市分别为安阳、菏泽、邢台、邯郸和晋城。此分析法和熵值法的评价结果基本一致，均显示北京市的空气质量最佳，在“2+26”城市中排名第一。

4 结 语

在参考相关文献的基础上,选取2017年10月至2018年3月间的月平均AQI及w(PM2.5)、w(PM10)、w(SO2)、w(CO)、w(NO2)、w(O3)，共7个指标进行空气质量评价。

利用熵值法计算出“2+26”城市空气质量指标的权重以及综合得分，最终得出空气质量的排名情况。其中，空气质量较好的前5个城市分别为北京、廊坊、天津、开封和滨州；空气质量排名靠后的5个城市分别为安阳、晋城、石家庄、邯郸和邢台。

同时，采用因子分析方法提取主要因子，对空气质量给出解释和评价。结果显示，空气质量最好的前5个城市分别为北京、廊坊、天津、郑州和鹤壁，空气质量最差的5个城市分别为安阳、菏泽、邢台、邯郸和晋城。

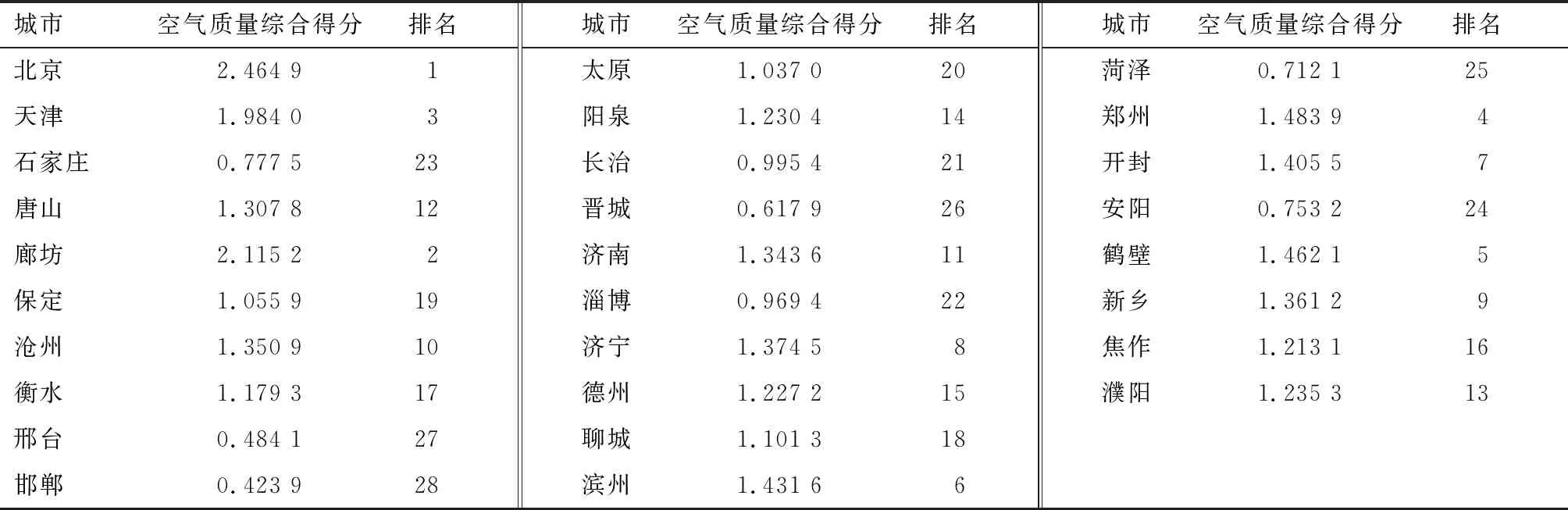
表8 采用因子分析法所得“2+26”城市空气质量评价结果

两种方法的评价结果均显示北京空气质量最佳，结果基本一致。

提升空气质量，是满足人民美好生活需要的重要举措。将熵值法和因子分析法应用于空气质量评价,能够为提升空气质量提供相关参考。