基于ARIMA和CART的负载预测模型

王电钢，黄 林，常 健，梅克进，牛新征

1) 国网四川省电力公司信息通信公司，四川成都 610015; 2)电子科技大学计算机科学与工程学院，四川成都 611731

随着业务量的上升，服务器主机上的负载压力不断增大，而长时间处于高负载状态不利于主机设备的稳定运行，需要运维操作人员及时发现并释放资源，这对运维工作带来了困难．虽然现有的运维监控系统中已有对CPU和内存等的监控功能，并可以通过设置告警阈值提醒运维人员，但这种事后处理的方式具有一定滞后性，存在问题处理不及时的风险．因此，对CPU和内存等资源的历史负载信息和波动模式进行分析挖掘，并预测未来一段时间的负载趋势，对于智能化运维工作是极其重要的．负载的趋势预测有助于提高运维工作的预见性，为运维人员制定解决方案提供一定的缓冲期，对于可能出现的问题防患于未然．

对于负载预测的研究，目前主流的方法是利用历史数据建立线性预测模型．然而在实际工作中，主机负载受复杂的内外部环境影响，如温度、网络、业务量和硬件状况等．真实的主机负载信息并不严格满足线性关系，存在一定的非线性部分，而现有的一些方法并未对非线性部分进行预测，预测效果较差．如李刚等[1-3]基于特定范围内的历史数据，采用自回归差分滑动平均(autoregressive integrated moving average，ARIMA)模型来预测未来特定范围的值，可以较好地拟合线性部分，但并未考虑非线性部分，丢失了部分模型精度．此外，虽然部分研究提出不同的参数估计方法来提升模型精度．如单锐等[4-5]提出基于改进谱共轭梯度的ARIMA模型参数估计法，通过调整参数，使得算法满足充分下降条件或者共轭条件，达到优化的目的．张宗华等[6]提出了基于加权改进的AR模型的负载预测，他认为不同时间点对当前时间点的影响不同，离当前时间点距离越近，通常对预测造成更大的影响，应在不同的时间点上分配不同的权值，让影响更大的点拥有更大的权值，减小偏远点的影响，提升精度．上述方法尽管在不同层次上提升了模型对负载数据的预测效果，但是这种提升仅体现在对模型线性部分的预测，并未真正解决数据中非线性部分的预测问题．为此，本研究提出将负载数据分解为线性部分和非线性部分，并分别对两部分进行训练和预测，采用基于加权最小二乘参数估计方法[7]的线性模型ARIMA[8]预测负载数据的线性部分，采用基于Fayyad边界判定[9]优化方法的分类回归树[10-11](classification and regression tree，CART)模型拟合负载数据的非线性部分，最后将预测结果融合，提升预测精度．

1 负载预测模型

给定数据集D={x1,x2, …,xt}， 其中，xt表示以负载数据作为时间序列时t时刻的负载值，负载预测模型解决的是t时刻后续的多个数据值的预测问题．

1.1 ARIMA模型

ARIMA模型是一种基于时间序列的预测方法，它用某种数学模型将时间和预测对象组成的序列拟合起来．一旦模型确定后，就可以通过这个模型预测未来，被广泛应用在实际中，如就业发展趋势分析、机场客流量预测、疫情分析和负荷预测等．ARIMA模型满足

(1)

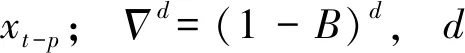
(2)

当模型中心化后，可简写为

xt=φ1xt-1+…+φpxt-p+εt-

θ1εt-1-…-θqεt-q

(3)

ARIMA模型的建模步骤如下：

1)首先用ADF[12]单位根检验法判断数据的平稳性．当数据不平稳时，对序列进行差分处理．差分阶数的选取方法一般为将其从1逐渐增大，直至序列满足ADF校验．

ADF单位根检验法：

如果序列经过d阶差分后平稳，不妨设

|λi<1|;i=1, 2, …,p

(4)

则

(5)

由式(5)可知，ARIMA模型共有p+d个根，其中，p个根在单位圆外，d个根在单位圆上．当d≠0时，ARIMA模型不平稳．

2)根据样本自相关函数ACF和偏自相关函数PACF的拖尾性和截尾性来确定p和q值．采用AIC[13]标准，选择使AIC达到最小值的自回归滑动平均模型(autoregressive moving average model，ARMA)进行拟合．AIC标准函数为

AIC=nlnL+2(p+q+1)

(6)

其中，L为似然函数．选择最佳p、q值使得AIC达到最小．

3)估计线性预测模型中参数的值．常用的方法是最小二乘法．

在ARIMA中，记

(7)

θ1εt-1-…-θqεt-q

(8)

其中，φi为自回归系数；θi为移动平滑系数；εi为零均值白噪声序列. 则残差项为

(9)

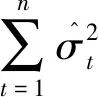
4)检验模型的显著性．如果拟合模型未通过检验，则转向步骤2)重新选择模型再拟合，直到残差序列为白噪声为止．

5)利用拟合的模型，预测将来的走势．

1.2 CART模型

CART是一种非线性的分类和回归模型．它能很好地处理高维数据，并筛选出重要的变量，具有良好的可解释性．在机器学习中，利用对象属性和对象值之间的映射关系，可以将回归树作为预测模型．但当训练集太大时，需要多次顺序扫描数据集，因此传统构造回归树的算法效率比较低．本研究对传统CART算法的分裂策略进行了优化．传统CART回归树的训练算法包括2个步骤．

1.2.1 CART的生成

CART的生成是决策树的核心问题之一，决策树的生长是反复分支的过程，当分支没有意义，即分支后结果差异不再显著下降，就不再分组．也就是说，分组的目的是为了使输出变量更加接近．在CART中，为了使预测的效果更好，通常使GINI值更小．GINI值为

(10)

其中，pi为在样本集中取到分类为Ci的子集的概率；l为子集数量．对于回归树来说，采用均方根误差来确定分法，均方根误差公式为

(11)

其中，xi为样本值；μ为样本均值；n为样本数量．σ越小，表明预测效果越好．因此要选择使回归方差最小的属性作为分裂方案．

1.2.2 剪枝

对决策树的精简，是另一个核心问题．回归树的剪枝是为了防止模型过拟合,CART使用CCP[14-15]算法进行剪枝，在训练集上计算表面误差增益率为

(12)

其中，R(t)为结点数t的错误代价，为

R(t)=r(t)p(t)

(13)

其中，r(t)为结点t的错分样本率；p(t)为所有样本中落入结点t的样本所占的比例；R(T)为子树T的错误代价；N(T)为子树中的结点数．CCP的剪枝策略为取出最小指标α对应的节点，将其剪掉，生成第1个子树，重复这个过程，直到只剩下根节点时，将其作为最后一个子树．然后利用验证集去验证所有子树，取误差最小的树．

1.3 基于ARIMA和CART的负载预测模型

运用组合模型对负载序列进行预测，存在两个关键点：

1)需要通过ARIMA模型较好的拟合序列中存在的线性因素，使序列的线性因素基本提取完全．因此，本研究在传统ARIMA模型参数估计方法上做了优化，采用加权最小二乘估计法来消除异方差性，使得参数估计更加准确，模型拟合更好．

2)当拟合完序列中存在的线性因素后，需要对残差序列的非线性因素进行提取，本研究采用CART来拟合非线性因素，降低了训练时间，并且分类更为简单．

1.3.1 加权最小二乘的ARIMA参数估计

定义wi为滞后i阶的数据的权重，我们认为，残差更大的项占有的权值应该更低，这样能使误差更小．为了消除正负号带来的影响，用残差的平方来表达，即

(14)

以此构建对角权重矩阵[16]

(15)

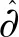
(16)

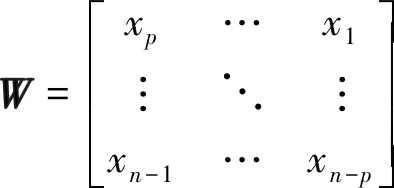
(17)

xi为时间序列；Y为预测时间t前真实值组成的(n-p)×1矩阵．

1.3.2 基于边界判定的CART分裂策略

Fayyad边界点判定与熵[17]有关，其熵越小，对属性进行分类所需的平均信息量就越少．熵值为

(18)

其中，pi表示在样本集中取到分类为Ci的子集的概率. 由于熵值和GINI系数的变化趋势相同，因此，要找到最小GINI系数，只需要找到使平均类熵达到最小的值．由Fayyad边界点判定原理可知，该值在排序后两个相邻异类样本之间．本研究的CART分裂属性为连续属性，所以每次只需要找出一个将属性取平均值后的分界点作为分割阈值，将样本集分为两边，此时，阈值点即为该分界点．此方法并不需要计算每个分割点的GINI系数，大大提升了训练效率．只有当出现属性值达到最小这种不理想情况时，才会与原来的分类次数相同．

1.3.3 组合算法

通过改进的ARIMA模型得到预测数据和历史数据的线性组合，即式(3)．由于εt参数的不可获得性，所以xt的估计值为

(19)

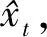
(20)

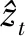
由式(20)得到负载数据的非线性部分后，需要利用改进的CART回归树对滞后期从1到p阶的历史数据进行残差拟合训练，提取序列中的非线性关系，得到拟合更为准确的非线性关系，即

(21)

最终i时刻的观测值可以表示为

(22)

具体算法为：

步骤1：数据预处理，并通过AIC标准确定最优阶数p、q；

步骤2：通过加权最小二乘参数估计法得到ARIMA的相应参数，得到线性预测模块ARIMA的预测模型；

步骤3：将观测值与预测模型的拟合值作差，得到残差序列；

步骤4：通过步骤一中所定阶数p， 用CART回归树将p个历史数据与对应残差进行训练；

步骤5：结合ARIMA模型和CART模型的预测结果，得到最终结果．

2 实验结果及分析

2.1 实验数据集

本研究采用不同采样频率的CPU和内存负载数据，采集自某企业真实的主机(表1)．算法采用Python实现，实验环境为Windows8.1、Intel Core i7-4510CPU@2.60 GHz、4 Gbyte内存．

表1 实验数据集

2.2 实验结果

本研究在采样频率为5、10和20 min的CPU负载上进行训练，并预测未来的40个数据，与传统ARIMA模型进行对比，实验结果如图1至图3．

图1 CPU_5负载预测结果对比Fig.1 (Color online) CPU_5 load prediction results comparison

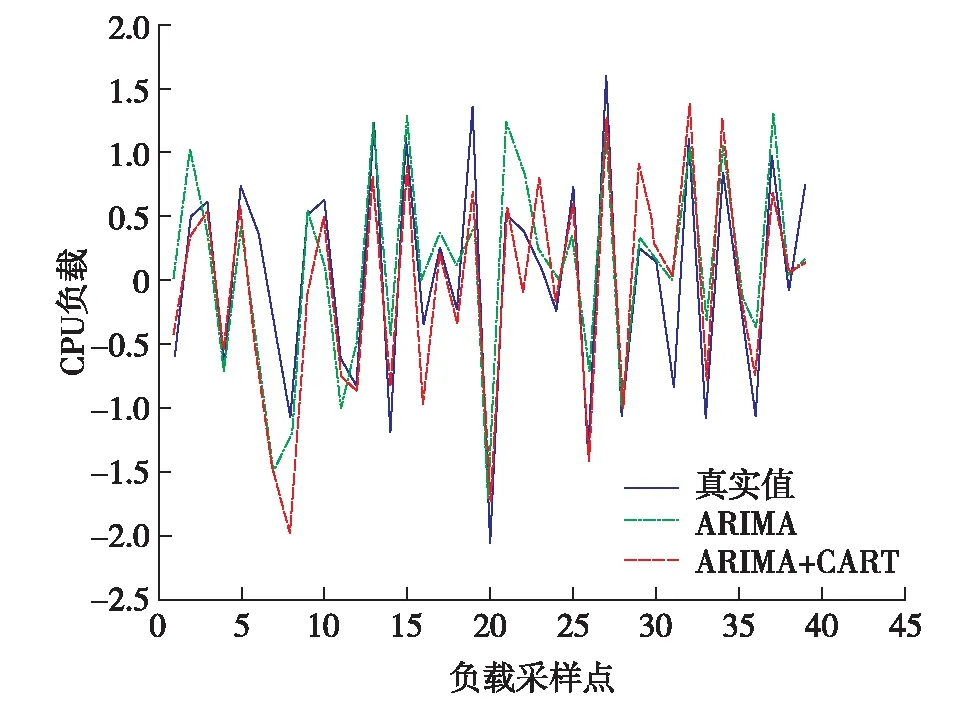
图2 CPU_10负载预测结果对比Fig.2 (Color online) CPU_10 load prediction results comparison

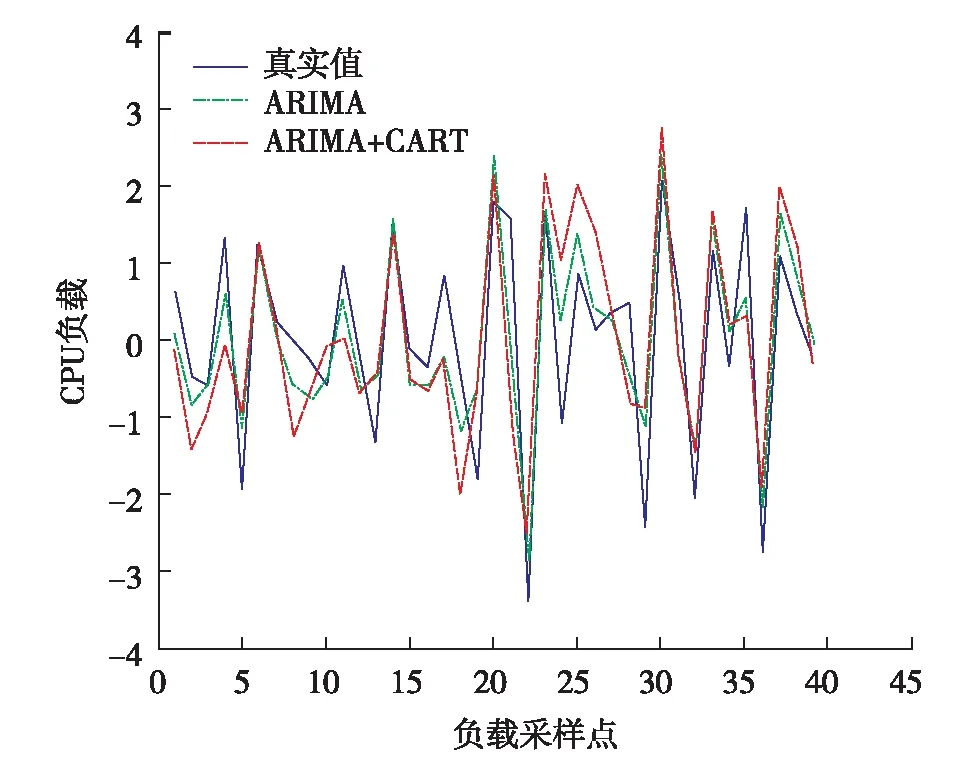
图3 CPU_20负载预测结果对比Fig.3 (Color online) CPU_20 load prediction results comparison

从图1至图3可见，ARIMA+CART组合模型对偏远点的预测均比ARIMA模型准确，整体的预测效果也要比ARIMA模型好．这是由于它预测了负载数据中的非线性部分，更接近实际数据分布．

进一步，以不同采样间隔的内存负载数据分别对ARIMA模型和ARIMA+CART组合模型进行训练并预测，实验结果如图4至图6．

图4 内存_5利用率预测结果对比Fig.4 (Color online) Memory_5 utilization rate prediction results comparison

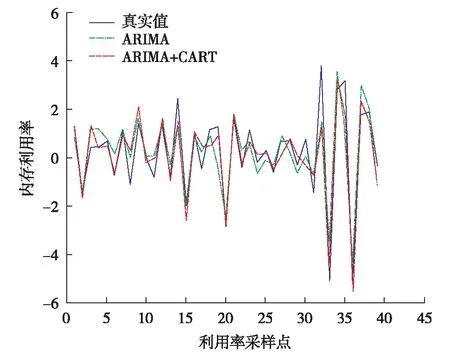
图 5 内存_10利用率预测结果对比Fig.5 (Color online) Memory_10 utilization rate prediction results comparison

图 6 内存_20利用率预测结果对比Fig.6 (Color online) Memory_20 utilization rate prediction results comparison

从图4至图6可见，ARIMA+CART组合模型的预测均比ARIMA模型准确，这是由于组合模型拟合了残差中含有的非线性因素，所以比ARIMA更贴近真实值，误差更小．在不同时间间隔的内存利用率数据中，组合模型同样有更好的效果．

为了量化本研究算法的预测精度，我们采用平均绝对误差和作为评价标准，即

(23)

通过分析实验数据，得到ARIMA模型和ARIMA+CART组合模型的负载预测误差，如表2．

表2 不同模型的负载预测误差对比

从表2可见，ARIMA+CART模型相比ARIMA模型的预测误差有明显降低，预测精度比传统ARIMA模型提高了15%以上，证明了本研究模型的预测精度更高．

结 语

本研究提出基于加权参数估计法的ARIMA和CART的组合负载预测模型，较单一线性模型而言，CART解决了负载数据中非线性部分的预测问题，模型预测精度得到明显提升．实验结果证明，本研究模型对一些波动较大的偏远点预测要更优于单一线性模型，这是由于CART对残差的非线性部分的预测弥补了线性模型的缺陷，使得模型的最终预测值要比传统模型更靠近真实值，整体的预测精度提高了15%以上．