基于稀疏表示模型的显著目标检测

张 萌, 陈晓云

(福州大学数学与计算机科学学院, 福建 福州 350108)

0 引言

图像数据是人们接收信息的主要渠道之一， 但在丰富杂乱的图像数据中， 人们只关注图像最吸引人的部分. 显著目标检测是检测和分割图像最吸引人注意部分的一种技术. 鲁棒主成分分析[1](robust principal component analysis, RPCA)是一种基于无监督学习的显著目标检测方法.

鲁棒主成分分析将图像分解成低秩背景和稀疏显著目标， 但是该方法只能检测到显著目标的边缘， 因此文献[2-3]根据图像的先验信息为显著目标特征矩阵加权从而获得显著目标的整个区域， 但是区域内的显著值不一致问题无法解决. 为此， 文献[4]用加权的结构树稀疏正则项代替稀疏项， 并引入拉普拉斯正则项增大显著目标与背景的差别； 文献[5]增加不同特征之间的差异互补信息； 文献[6]加强背景特征矩阵的低秩性和显著目标的稀疏性， 突出显著目标.

上述方法在显著目标内部出现不同颜色时， 不能生成一致的显著值. 为此， 基于RPCA模型， 本研究提出基于稀疏表示模型的显著目标检测方法(sparse representation model for salient object detection， SRMSOD). 通过约束显著目标的稀疏自表示系数平滑目标内部不同的显著值， 同时引入拉普拉斯图正则项来刻画显著目标.

1 相关工作

首先概要介绍RPCA模型[1]. 对给定矩阵F∈Rd×N， RPCA将F分解成低秩矩阵加稀疏矩阵， 即

(1)

在显著目标检测中，F是图像的特征矩阵，L是背景特征矩阵且低秩，S是显著目标的特征矩阵且稀疏，d是特征维数，N是图像分割成不重叠的部分的个数(每个部分称为超像素). 某一超像素Pi的显著值按以下公式计算

其中：Si是显著目标矩阵S的第i列. Sal(Ρi)越大, 表示Ρi属于显著目标的概率越大.

2 基于稀疏表示模型的显著目标检测方法

由于显著目标颜色不同时RPCA模型得到的目标显著值不一致， 本研究引入显著目标特征矩阵的稀疏自表示[7]， 提出SRMSOD. 该方法用目标的自表示系数矩阵代替目标的特征矩阵， 同时加入图正则项保持显著目标超像素的近邻关系， 使特征相似的超像素有相似的表示系数.

2.1 稀疏表示

稀疏自表示[7]假设同一子空间的样本能被除自身以外的样本线性表示， 不同子空间的样本不能互相表示， 其模型为

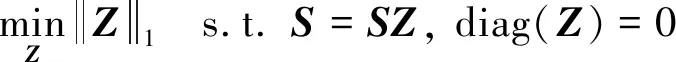
(2)

其中：S=[s1,s2, …,sN]∈Rd×N是样本矩阵，Z∈RN×N是系数矩阵. 对同一子空间的超像素， 颜色越接近， 相应的表示系数越大.

2.2 模型建立

假设显著目标的任意两个超像素的特征向量为si和sj， 其表示系数为zi和zj， 定义以下图正则项

(3)

其中:wij表示超像素Pi和Pj的相似度， 相似度越大， 对应的表示系数越接近. 定义方式为

(4)

则基于SRMSOD模型为

(5)

2.3 模型求解

该模型有3个变量L,S,Z， 可用ADMM算法解决. 引入辅助变量K,H来分离变量， 将公式(5)转化为以下等价问题

(6)

其对应的增广拉格朗日函数为

其中:Y1,Y2,Y3,Y4为拉格朗日乘子;μ>0是惩罚参数. 在求解过程中, 固定其余变量， 交替更新其中一个变量, 具体更新过程如下.

1) 固定其余变量， 更新变量L.

(8)

该式最后会收敛到局部最优点σ*[8], 故式(8)的解为

Lt+1=Udiag{σ*}VT

(9)

2) 固定其余变量， 更新变量H.

(10)

式(10)是一个强凸问题， 令此问题的一阶导数为0， 得到：

(11)

3) 固定其余变量， 更新变量K.

(12)

式(12)可通过阈值算法[10]求解， 则

(13)

4) 固定其余变量， 更新变量Z.

式(14)是一个强凸问题， 令此问题的一阶导数为0， 得到：

(15)

5) 固定其余变量， 更新变量S.

式(16)是一个强凸问题, 令此问题的一阶导数为0， 得到：

(17)

2.4 显著图生成

上述所有变量更新一次的时间复杂度为O(n3)， 算法得到显著目标特征矩阵S后计算每个超像素Pi的显著值Sal(Pi). 受文献[11]启发， 根据背景先验概率以及背景区域和目标区域超像素的分散程度不同对各超像素的显著值进行优化， 使最终显著图的背景更干净. fsali为超像素Pi优化后的显著值， 优化模型[12]如下：

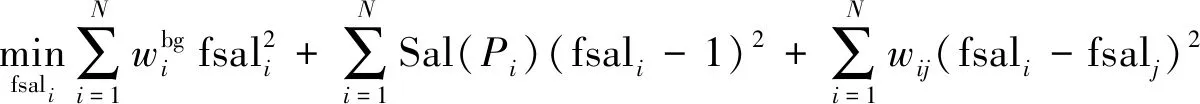
(19)

用color boosted Harris point(CBHP)算子[13]和色调算子分别检测图像的显著点， 取对应显著点分别围成的凸包的交集为最终凸包. 在最终凸包内的所有超像素定义为前景， 剩余部分定义为背景， 然后分别对前景和背景做层次聚类， 把小于相似性阈值τ的超像素聚成一类， 记为区域Ok， 每个超像素Pi必然属于某个Ok.

1) 背景先验概率.

其中:Pi∈Ok，Nb是既属于Ok又属于边界的超像素个数，Nc是属于Ok的超像素个数. 这样属于同一区域的超像素就有相同的背景先验概率.

2) 区域超像素的分散程度. 根据颜色特征聚类形成区域Ok， 可能包含空间距离远但颜色相近的超像素. 因此， 超像素Pi与同一区域其他超像素的空间距离之和体现Pi与其他超像素的分散程度， 故

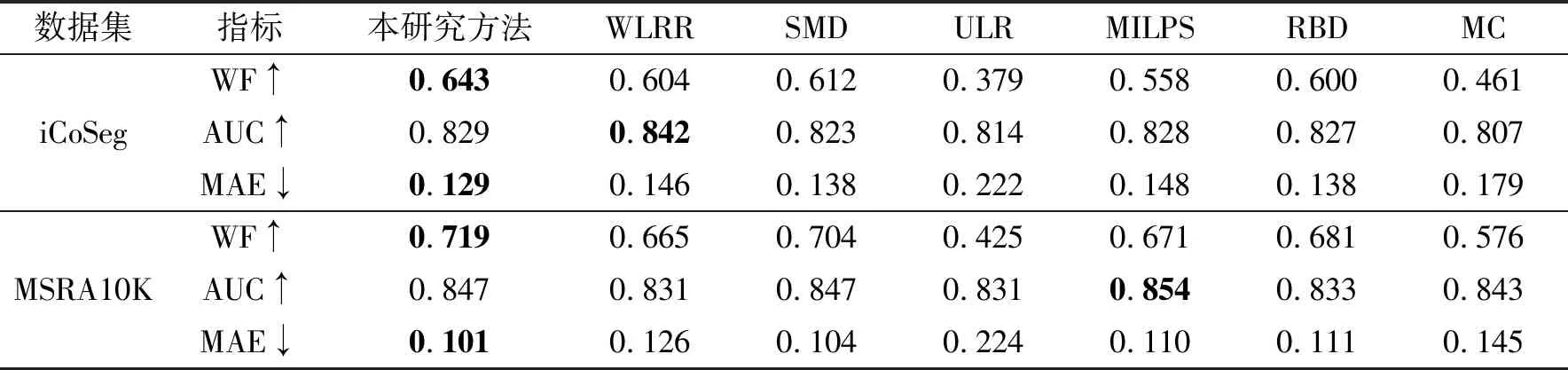
本研究算法步骤如下:输入. 特征矩阵F, 参数α, β, γ和每个超像素的权重wbgi.输出. 最终显著图S∗.初始化. L0=0, S0=0, H0=0, K0=0, Z0=0, Y01=0, Y02=0, Y03=0, Y04=0, μ0=0.1, μmax=1010 , ρ =1.1 , t =0 , ε =10-5. 1. 循环直至满足收敛条件 Step1. 利用公式(9)更新L. Step2. 利用公式(11)更新H. Step3. 利用公式(13)更新K. Step4. 利用公式(15)更新Z. Step5. 利用公式(17)更新S. Step6. 利用公式(18)更新拉格朗日乘子Y1, Y2, Y3和Y4. Step7. 更新惩罚参数μt+1=min(ρμt, μmax) Step8. 终止条件: F-L-SF

3 实验结果与分析

本研究提出的SRMSOD在常用的显著目标数据集iCoSeg[15]和MSRA10K[16]上进行评估. iCoSeg作为多个显著目标数据集的代表， MSRAK10K作为单个显著目标数据集的代表， 两个数据集均从官方网站下载， 包含原始图像和真实的显著图(ground truth, GT)， 各自的特点分别如表1所示. SRMSOD模型与WLRR模型[6]、 SMD模型[4]、 ULR模型[2]、 RBD模型[12]、 MC模型[17]、 MILPS模型[18]共6种显著目标检测方法比较. 其中， WLRR模型、 SMD模型和ULR模型是基于低秩矩阵恢复的方法， MILPS模型是近年提出的性能较好的方法.

表1 显著目标检测数据集描述

3.1 参数设置和评价指标

本研究方法与上述提到的6种对比方法都在Intel(R)Core(TM)i7-7700 CPU 3.60 GHz, 内存32 G环境下， 由Matlab R2015a编程实现. 6种对比方法的参数均采用原作者设定的参数， 本研究模型的参数设定为超像素个数N=300， 带宽参数[4]σ2=0.05, 平衡参数α=1.2 ,β=0.35， 可调节反正切函数的参数γ=20. 并采用准确率-召回率(precision-recall, PR)曲线、 F-measure曲线, 加权F-measure(WF)[19], AUC(ROC曲线下面积)和平均绝对误差(mean absolute error, MAE)[20]对本研究方法与对比方法进行评估.

PR曲线和F-measure曲线主要关心显著目标是否被正确检测， 而MAE则关注生成的显著图S*与GT之间的差异， 即： MAE=mean(S*-GT).

3.2 结果分析

为评估本研究方法的有效性， 将其与对比方法在2个显著数据集上进行实验， 实验结果见图1. 从图1可以看出， 在两个数据集上， 本研究方法的PR曲线和SMD、 MILPS方法的曲线十分接近， 都在其他方法的上方， 但是在F-measure曲线上， 略优于SMD方法和MILPS方法， 且明显好于其他方法. 这说明得到的准确率略高于SMD方法和MILPS方法， 因为Fβ更重视准确率， 所以该方法的F-measure曲线更宽更高.

图1 2个数据集的PR曲线和F-measure比较 Fig.1 Comparison of PR curves and F-measure results on two datasets

2个数据集上的WF、 AUC和MAE实验结果见表2. 由表2知， 本研究方法的WF和MAE指标在2个数据集上都是最优的. AUC指标在iCoSeg数据集上是次优的， 在MSRA10K数据集上略逊于MILPS方法. MAE指标能侧面反映显著目标内部的显著值是否一致. 该方法的MAE值最小， 因为稀疏自表示系数考虑到显著目标的内部关系， 即在显著目标出现不同颜色的情况下， 能在显著目标内部生成更一致的显著值. 接下来从视觉角度对比所有方法的显著图， 详见图2所示. 从图2不难发现， 无论是多显著目标还是单显著目标， 当显著目标出现两种及以上的颜色时， 采用本研究方法的显著图更一致高亮， 不同颜色区域的界限不会分明.

表2 2个数据集上的WF、 AUC和MAE指标结果

注: ↑表示指标值越大越好， ↓表示指标值越小越好

图2 不同方法得到的显著图对比(GT为真实的显著图)Fig.2 Comparison of saliency maps of different methods

4 结语

本研究提出基于稀疏表示模型的显著目标检测方法， 学习显著目标的稀疏自表示系数， 同时引入拉普拉斯图正则项， 使显著目标的显著值趋于一致. 在2个显著数据集上的实验结果表明， 所提方法对显著目标出现不同颜色的图像， 能产生更一致高亮的显著图.