新型浮筏式防波堤消波性能试验研究

葛 聪，王国玉，张 琪，赵银林

(大连理工大学 海岸和近海工程国家重点实验室，大连 116024)

由于受到技术以及造价的限制，传统式防波堤已经不能适应深水海域的要求。目前各国正通过研究具备经济、生态、施工便利、消波效果好的新型防波堤，来解决海岸工程相关问题。浮式防波堤是一种由浮体和锚泊系统组成的结构，其通过反射或者消散入射波能量来掩护后方区域，常见的结构型式有浮箱式、浮筒式和浮筏式防波堤。由于浮式防波堤存在相对传统式防波堤造价小、施工方便、对环境影响小等优点和消波效果较差，特别在自振频率附近结构运动响应大、易疲劳受损等缺点[1-3]。因此，近年来各学者对新型的浮式防波堤开展了许多研究。

Pena[4]等通过物理模型试验研究了改变浮堤宽度、侧翼长度等参数对放置在巴约纳港口浮筒式防波堤原堤消波效果的影响。试验结果表明浮堤的宽度对透射系数影响大，增加侧翼长度对其的影响很小。Bayram[5]提出了一种倾斜浮筒防波堤，该结构的消波效果对波高不敏感，倾斜角度是影响透射系数的主要因素。Cheng[6]等研究了一种由PVC管组成的凹状菱形管新型的浮式防波堤，数据表明相对宽度越长透射系数越小。Cheng[7]研究了一种用于掩护深水水产养殖的浮式防波堤，该防波堤由28个标准模具(包括双体筏、消波装备和减振设施)以及锚链系统组成。并通过试验测试了其消波效果，结果表明其消波效果可达到50%。Hegde[8]等人通过物理模型试验对由三层PVC管水平交错排列的浮式防波堤的波浪损耗进行了研究。Koraim[9]通过物理模型试验对一种由半圆管组成一排或多排的浮式防波堤进行了研究，该试验结果表明，水平半圆管防波堤消波效果好于平板，透射系数能相对于平板降低5%～25%，能量损耗系数能高于5%～25%。Ji[10-11]等通过物理模型试验和建立数值水槽对几种新型的浮筒式防波堤进行了研究。与传统的双浮筒防波堤相比该结构的消波性能更好，尤其对于长周期和大波高的情况。但即使是改良后的双浮筒防波堤，长周期波浪条件下消波效果仍不佳。金凤[12]等对由框架结构以及水平和垂直的开孔薄膜组成的多级带孔薄膜浮式防波堤进行了研究，该结构对短波掩护效果好，但对长波效果较差。郑启航[13]等在金凤的基础上对框架带孔薄膜浮式防波堤单元体的消波效果进行了研究。通过对单元体进行拼装，其结构消波效果良好，消波系数均可达到0.4～0.6。

虽然，很多学者都致力于研究能提高消波效果的新型浮式防波堤，但是目前的研究十分有限，在理论研究与实际应用中还存在很大的差距。本文提出了一种新型浮筏式防波堤(以下简称浮堤)，旨在通过二维物理模型试验来研究其消波效果，以期对实际应用提供参考。

1 模型设计

1.1 模型结构

模型采用单元模块组装型式的防波堤结构，单元模块由PVC加强复合布制成的波纹形水囊和钢筋笼组成，其具体结构型式如图 1所示。波纹形水囊未充水尺寸为0.75 m×0.75 m(长×宽)，充水后尺寸为0.69 m×0.71 m×0.04 m(长×宽×高)。水囊波纹垂直于波浪传播方向，其波纹形的表面能增加底摩擦损耗波能。模型钢筋笼采用直径6.0 mm的圆钢，其重量为0.222 kg/m。为使模型起浮，本试验在钢筋笼两侧布置了起浮泡沫。

1-a 钢筋布置图1-b 模型与钢筋布置图图1 单元模块结构图(单位:m)Fig.1 Structure of unit model (unit: m)图2 波浪动能(线性波理论)分布图(d=0.4 m,H=0.04 m)Fig.2 Distribution diagram of kinetic energy of wave based on the linear wave theory(d=0.4 m,H=0.04 m)

具体防波堤结构是由3块模块单元组装而成，其浮堤总宽度W(W=W1+W2)为2.1 m。通过改变组装迎浪侧倾斜宽度、前端入水深度设计了如表1所示的5种结构模型，单元模块之间的连接采用工程上常用的刚性铰接方式。其中，在设计模型倾斜段前端入水深度时，是基于波浪在斜坡处发生波浪破碎时消耗50%的动能能量以及破碎指标综合考虑。图2给出了在水深d=0.4m，波高H=0.04 m条件下，波浪平均动能随纵向位置z(z=0表示在水面，z=0.4 m表示在水底)的分布图，从图中可知，各周期动能损耗率为50%时所对应的前端入水深度ds范围为(0.07，0.16)m。根据实际情况，选取破碎指标H/d=0.5，得d≤0.10 m，即斜坡段存在坡上水深小于0.10 m的区段波浪即可破碎。综合两者，最终选取ds=0.18 m。

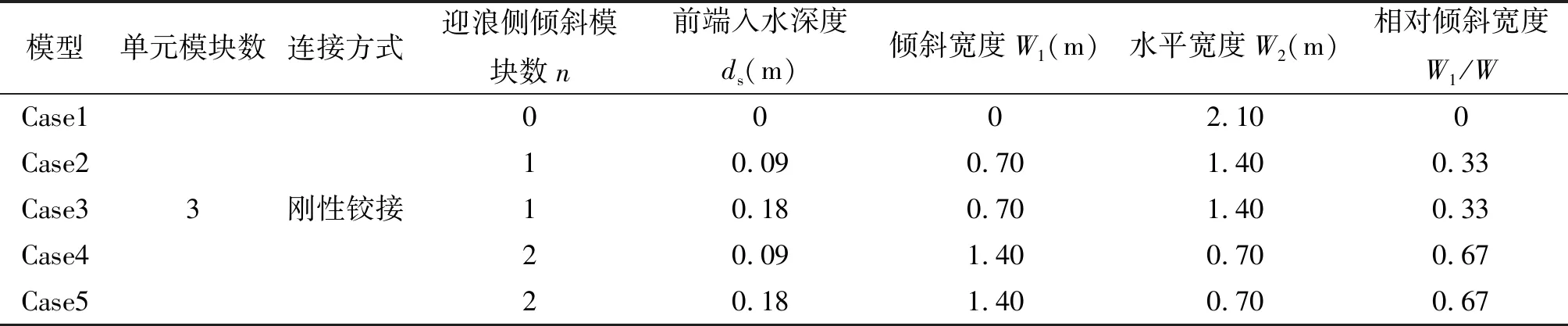
表1 模型参数表Tab.1 Parameter table of model

试验中模型用锚链进行固定，根据弹性、重量、长度等条件相似来设计。其最终采用直径为3 mm，刚度为47.16 N/cm，水下重量为150 g/m的锚链，布置方式采用平行布置。Case1的左右两侧锚链长度均为1.2 m，锚固点距离结构1.1 m。由于在分析悬链线长度对浮式防波堤水力特性的影响时，是将其与水深的比值来进行考虑，并且其比值对防波堤的影响很小甚至可以忽略[14]。因此，在本试验中将不会因锚链长度的需要而改变锚固点位置，Case2～5迎浪侧的锚固点均距模型0.55 m，锚链长度根据角度需求确定，背浪侧的锚链布置与Case1一致。

1.2 浮力计算

图3 模块起浮图Fig.3 The floating figure of model

由于钢筋笼不能自动在水中悬浮，同时，结构在运动过程会对周边水槽壁有较大的损坏作用，因此需要设计起浮的材料来提供浮力以及钢筋笼和水槽壁间的缓冲作用。对于水平布置的模块，主要考虑在满足一定浮力富余条件下(模块的配重密度小于水的密度)设计起浮的材料尺寸。对于倾斜布置的模块，存在模型剩余浮力大锚链预张力大的现象。为保证锚链安全，因此在设计时尽量满足模块浮力与自身的重力相等。其具体参数如表 2所示，起浮效果如图3所示。

表2 单元模块浮力计算相关参数表Tab.2 Parameter table of buoyancy calculation for unit model

2 物理模型试验

2.1 设备和布置

物理模型试验在大连理工大学海岸和近海工程国家重点实验室的大波流水槽中进行，该水槽长69 m、宽2 m、深1.8 m。水槽前端配备有实验室研制的电机驱动式造波系统，可造出波形稳定、重复性好的规则波、椭圆余弦波和不规则波。水槽后半段用隔板将其分隔为1.2 m和0.8 m两部分，能减少波浪二次反射。水槽末端装有消浪网，能减少波浪反射。波浪数据通过中国水利水电科学研究院研制DJ800多功能监测系统进行采集，该系统由计算机、多功能检测仪和多种传感器组成的数据采集和处理系统组成。

俯视图

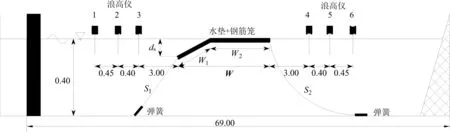
侧视图图4 模型布置图(单位：m)Fig.4 Sketch of model setup(unit :m)

试验结构位于0.8 m宽度段内，模型前端放置3个浪高仪1#、2#和3#，间隔分别为0.45 m、0.40 m，用来记录模型前波面过程线，通过采用Goda两点法计算模型的反射系数。基于水槽后端波浪反射不能完全消除，因此在模型后端放置三个浪高仪4#、5#和6#，间隔分别为0.40 m、0.45 m，通过Goda两点法计算模型的透射系数。3#、4#浪高仪与模型距离均为3 m，具体模型布置如图4所示。

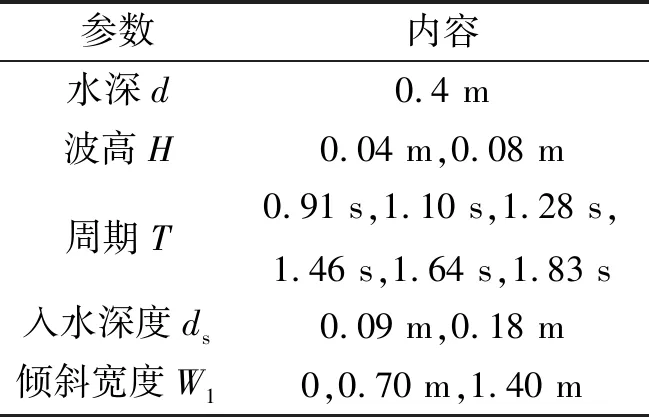
表3 试验组次Tab.3 Groups of test

2.2 试验条件和组次

试验水深为0.4 m，入射波浪为规则波。试验共5种模型，对于每种模型，波高有0.04 m和0.08 m两种，周期均包括0.91 s,1.10 s,1.28 s,1.46 s,1.64 s,1.83 s六种，试验工况共60组。具体组次见表3。

2.3 试验现象

本试验中，根据模块布置方式的不同，其波能损耗现象主要分为两种，具体如下所示：(1)对于水平放置的模型，波浪传至结构后，首先受到结构对其横向运动的阻碍越上结构，随后水质团由于纵向运动受阻形成如图 5所示的紊流，紊流形成后继续向前流动，由于结构表面底摩擦的存在进一步损耗能量。(2)对于有倾斜模块的模型，波浪传至结构后，由于浅水变形将发生图 6所示的波浪破碎损耗能量，破碎后的波浪也将因结构表面底摩擦进一步损耗能量。

综上，本试验结构能量损耗有以下几种原因：(1)波浪越上浮堤形成紊流；(2)结构表面有底摩擦，通过边界剪切力阻碍波浪传播；(3)波浪在结构上由于浅水变形致波浪破碎。

图5 浮堤上紊流图Fig.5 Turbulence on floating breakwater6-a 整体图6-b 局部图图6 浮堤上波浪破碎图Fig.6 Wave breaking on floating breakwater

2.4 数据处理

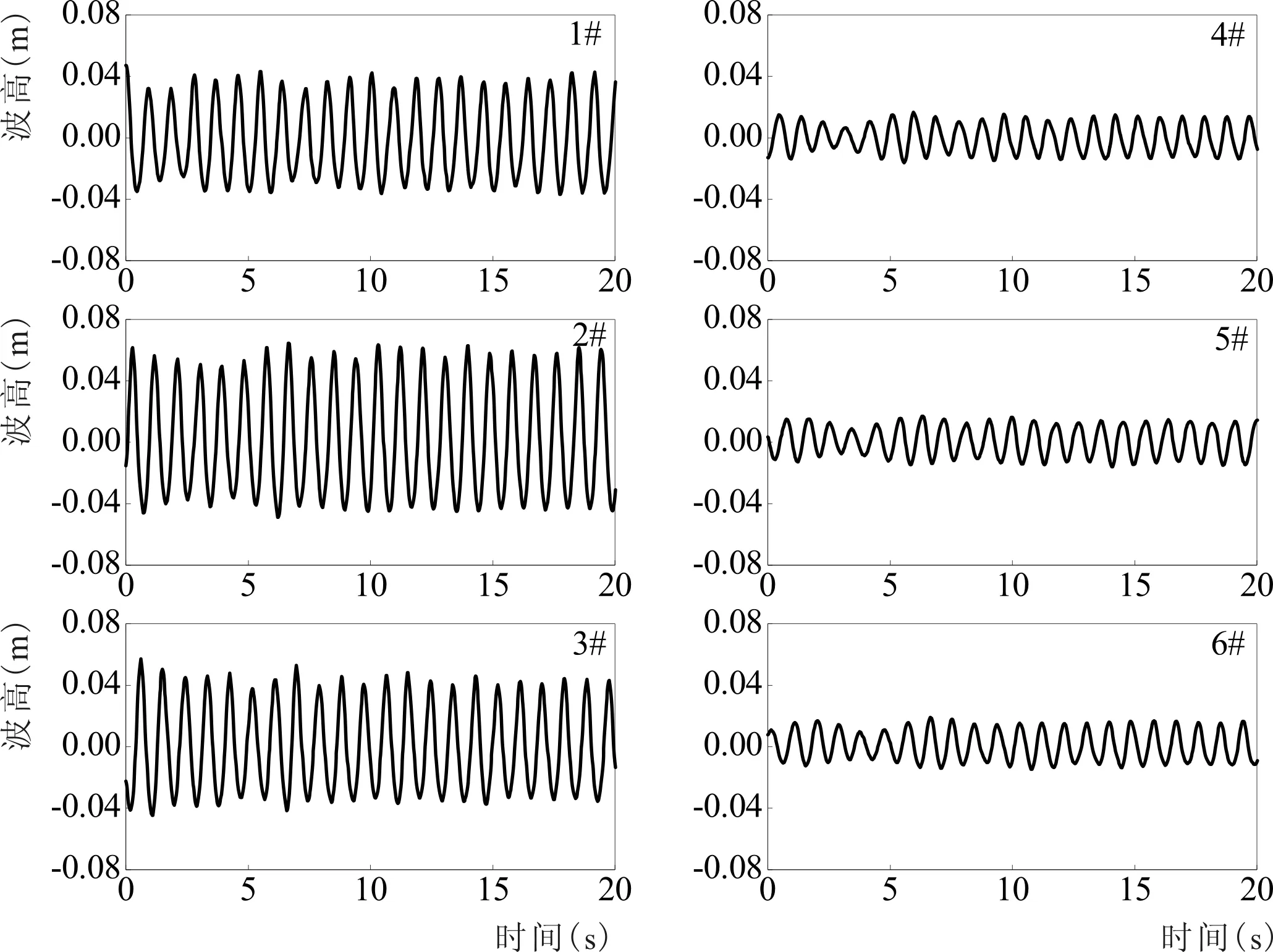
图7 波面历时曲线图(Case4，H=0.08 m，T=0.91 s)Fig.7 Time-series of wave elevation(Case4，H=0.08 m，T=0.91 s)

波浪传播至结构后，会发生波浪的反射、透射和能量损耗。因此，对于结构前方的波浪是入射波浪与反射波浪的叠加，需通过1～3号浪高仪根据Goda两点法进行分离，其反射系数Cr即为分离后的反射波高与入射波高的比值。对于结构后方的波浪，由于水槽末端的反射并不会完全消除，因此用4～6号浪高仪采用Goda两点法分离，波浪透射系数Ct即为堤后透射波高与堤前入射波高的比值。能量与波高的平方成正比，根据能量守恒，则有

(1)

根据上式，即可得能量损耗系数Cd。图 7给出了H=0.08 m，T=0.91 s时，Case4的波面历时曲线图。

3 试验结果分析

3.1 前端相对入水深度对消波性能的影响

图 8给出了在各周期波浪作用下，倾斜宽度W1=1.40 m时，新型浮筏式防波堤的透射系数和能量损耗系数与前端相对入水深度(ds/H)的变化关系图。图中ds/H=0，表示浮堤在迎浪侧没有布置倾斜模块。

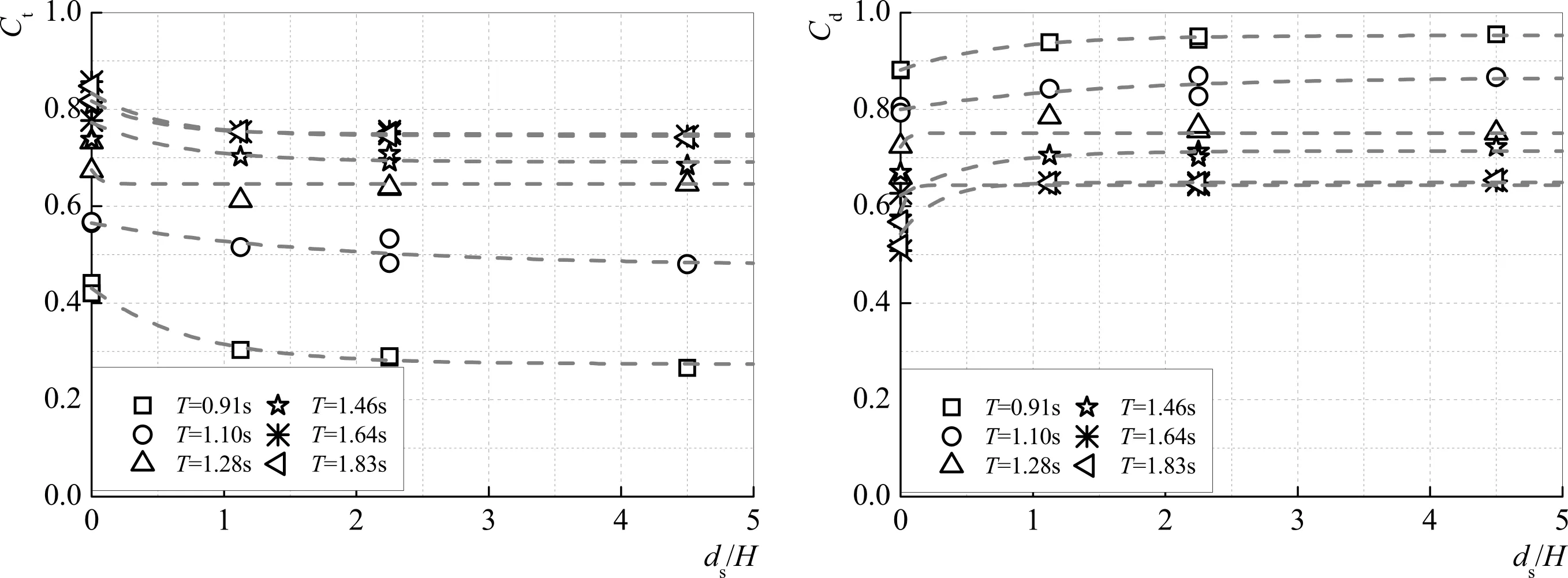
图8 Ct和Cd随ds/H的变化关系(W1=1.40 m)Fig.8 Variation of Ct and Cd with respect to ds/H(W1=1.40 m)

试验数据表明，透射系数与前端相对入水深度呈现两种变化关系。在ds/H<1时，Ct随着ds/H的增大而减小，在ds/H=1时，基本达到最小值，Ct的变化范围由原来的0.9～0.4减少到0.8～0.3。并且此种改善作用随着周期的变化而变化，在T=0.91 s时，改善作用最强，与ds/H=0的情况相比，Ct相对减少36%。随后ds/H>1时，Ct基本不随ds/H的变化而变化。

同样，能量损耗系数在ds/H<1时，随着ds/H的增大而增大。ds/H>1时，Cd不随ds/H的变化而变化。图中数据表明，ds/H>1的能量损耗系数比ds/H=0大，这说明前者相对损耗更多的能量。其原因为，对于水平放置的浮堤(ds/H=0)，波浪通过形成紊流损耗能量。而对于有倾斜模块的浮堤(ds/H>1)，除发生浅水变形使波浪破碎损耗较大能量外，其破碎后的波浪在后接模块上仍有紊流，会继续损耗能量，因此会损耗更多的能量。

综上所述，在试验范围内，当ds/H>1时，透射系数和能量损耗系数对于前端相对入水深度均不敏感。但是，与ds/H=0情况相比，增大ds/H能明显减小透射系数和增大能量损耗系数。

3.2 相对宽度对消波性能的影响

图9和图10给出了倾斜宽度W1=1.40 m时，不同前端相对入水深度下浮堤的透射系数和能量损耗系数与相对宽度的变化关系。与图 8相比，试验数据点更离散。也就是说，在本试验范围内，对于浮堤的消波性能，W/L比ds/H起到更大的影响作用。

9-a H=0.08 m9-b H=0.04 m10-a H=0.08 m10-b H=0.04 m图9 Ct在不同前端相对入水深度下随W/L的变化关系(W1=1.4 m)Fig.9 Variation of Ct with respect to W/L for different front relative draft (W1=1.4 m)图10 Cd在不同前端相对入水深度下随W/L的变化关系(W1=1.4 m)Fig.10 Variation of Cd with respect to W/L for different front relative draft (W1=1.4 m)

同时，试验数据表明，随着相对宽度的增加，透射系数整体呈现出逐渐减小而能量损耗系数逐渐增大的规律。透射系数变化范围为0.3～0.9，且当浮堤的宽度大于一倍波长时，透射系数可低于0.6。这是因为对于同一波高、同一水深、同一模型结构情况下，随着周期的增大，能量分布逐渐从水面向水底蔓延。而浮堤只能损耗水面附近限定水深区域内的能量，因此随着周期的增大也即相对宽度的减小，透射系数将增大，能量损耗系数将减小。

11-a H=0.08 m11-b H=0.04 m图11 Cr在不同前端相对入水深度下随W/L的变化关系(W1=1.4 m)Fig.11 Variation of Cr with respect to W/L for different front relative draft (W1=1.4 m)

图11为不同前端相对入水深度下浮堤的反射系数影响图。数据表明，结构的反射系数整体较小，其反射系数基本维持在0.2左右。这是因为对于水平放置的浮堤，其入水深度较小，因此能反射的能量较小。而对于有倾斜模块的结构，虽然前端入水深度增大，但是波浪传至结构后主要是发生浅水变形使波浪破碎。待波浪破碎后，能量减少，能反射的能量即会减少，因此整体的反射系数也较小。

3.3 相对倾斜宽度对消波性能的影响

本试验中，探讨了相对倾斜宽度对结构消波性能的影响。图12和图13分别给出了在ds=0.09 m、0.18 m条件下，相对倾斜宽度对透射系数、反射系数和能量损耗系数的影响图。

试验数据表明，相对倾斜宽度对浮堤的消波特性影响显著。相对倾斜宽度越大，透射系数越小，能量损耗系数越大，而反射系数则呈现出先增大后减小的趋势。

如前所述，在结构迎浪侧前端布置倾斜模块，能使波浪发生浅水变形。因此随着W1/W的增大，水下斜坡坡度变缓，波浪可破碎区段增大，能量损耗增大，透射系数减小。而对于反射系数而言，虽然W1/W的增大，能使能量损耗增多，使相对反射的波浪减少。但与此同时，W1/W的增大会使结构的挡浪面积增大，反射波高将增大。两者相互作用，则呈现出如上所述的规律。整体而言，增大相对倾斜宽度能改善浮堤的消波性能，下面进行具体的分析。

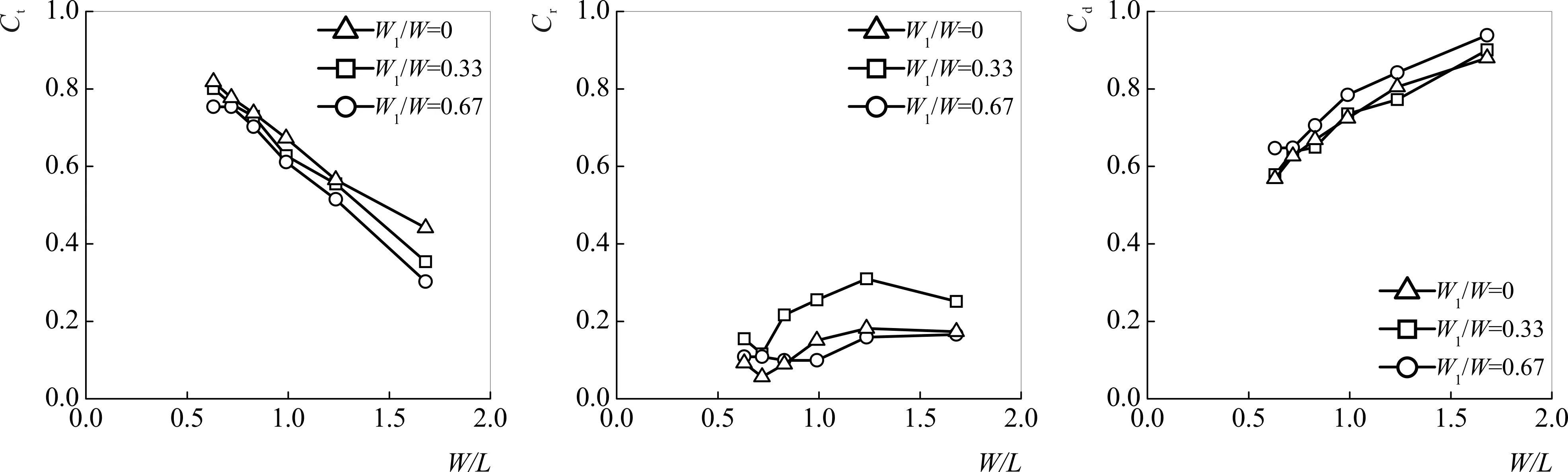
12-a H=0.08 m

12-b H=0.04 m图12 Ct、Cr和Cd在不同相对倾斜宽度下随W/L的变化关系(ds=0.09 m)Fig.12 Variation of Ct ,Cr and Cd with respect to W/L for different relative inclined width(ds=0.09 m)

在ds=0.09 m时，W1/W=0.33的情况比W1/W=0，Ct平均减小5.6%～11.4%；Cr平均增大42.3%～83.5%；Cd平均提高0.1%～10.5%。W1/W=0.67的情况比W1/W=0.33，Ct平均减小5.0%～5.7%；Cr平均减小38.9%～42.3%；Cd平均提高6.9%～7.0%。

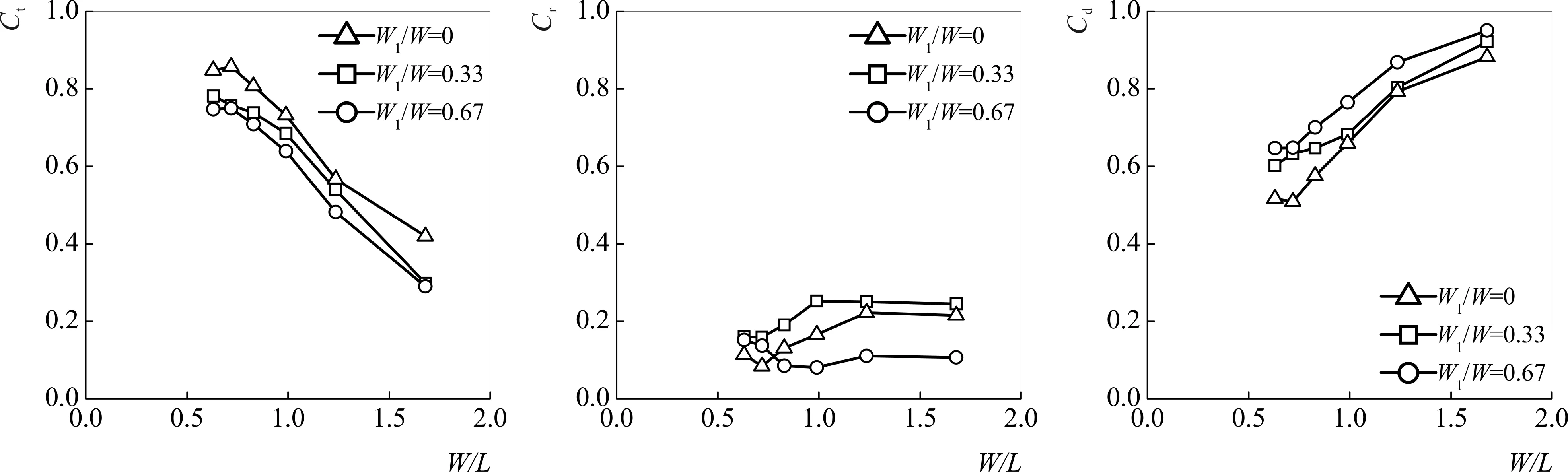
在ds=0.18 m时，W1/W=0.33的情况比W1/W=0，Ct平均减小8.9%～9.3%；Cr平均增大32.1%～67.3%；Cd平均提高2.4%～10.0%。W1/W=0.67的情况比W1/W=0.33，Ct平均减小1.4%～9.5%；Cr平均减小19.9%～27.9%；Cd平均提高3.8%～8.1%。

从以上数据可知，相对倾斜宽度的改变对反射系数的影响最大。在试验范围内，W1/W=0.33比W1/W=0，Ct平均减小5.6%～11.4%，Cr平均增大32.1%～83.5%，Cd平均提高0.1%～10.5%；W1/W=0.67比W1/W=0.33，Ct平均减小1.4%～9.5%，Cr平均减小19.9%～42.3%，Cd平均提高3.8%～8.1%；

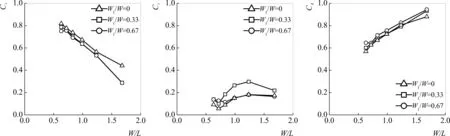
13-a H=0.08 m

13-b H=0.04 m图13 Ct、Cr和Cd在不同相对倾斜宽度下随W/L的变化关系(ds=0.18 m)Fig.13 Variation of Ct,Cr and Cd with respect to W/L for different relative inclined width (ds=0.18 m)

4 结语

本文对由三块模块单元刚性铰接组装的浮筏式防波堤的消波性能做了试验研究，研究结果如下所示：

在试验范围内，当ds/H>1时，前端相对入水深度对于透射系数和能量损耗系数影响较小。但是，与ds/H=0情况相比，增大ds/H能明显减小透射系数和增大能量损耗系数。

相对宽度对结构的消波效果影响显著，在相对宽度大于1时，透射系数低于0.6。

结构的消波特性对相对倾斜宽度敏感，其中相对倾斜宽度的改变对反射系数的影响最大。在试验范围内，增大相对倾斜宽度能明显减小透射系数、提高能量损耗系数，反射系数则呈现先增大后减小的规律。同时，在迎浪侧倾斜一块模块，透射系数比迎浪侧不布置倾斜模块平均减小5.6%～11.4%，能量损耗系数平均提高0.1%～10.5%，反射系数平均增大32.1%～83.5%。当迎浪侧倾斜两块模块时，透射系数能在一块基础上平均减小1.4%～9.5%，能量损耗系数平均提高3.8%～8.1%，反射系数平均减小19.9%～42.3%。