二元一次方程组中考考点聚焦

◎李中清

二元一次方程组是初中数学的重要内容，也是中考的热点。中考一般考查哪些知识点呢？现在就让老师带领同学们领略一番吧！

考点1 二元一次方程组的解

①+②，得

4a-4b=7，即4（a-b）=7。

【点评】已知方程组的解，常将解代入方程组，然后再求解。本题也可先解方程组得到a，b的值，然后再计算a-b。

考点2 列二元一次方程组

例2 （2018·荆州）《九章算术》是中国传统数学名著，其中记载：“今有牛五，羊二，值金十两；牛二，羊五，值金八两。问牛、羊各值金几何？”译文：“假设有5头牛，2只羊，值金10两；2头牛，5只羊，值金8两。问每头牛、每只羊各值金多少两？”若设每头牛、每只羊分别值金x两、y两，则可列方程组为（ ）。

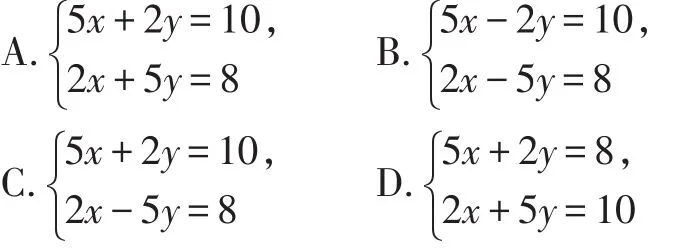
【解析】相等关系“5头牛，2只羊，值金10两”转化为方程是5x+2y=10；相等关系“2头牛，5只羊，值金8两”转化为方程是2x+5y=8，所以可列方程组为

【点评】列二元一次方程组解决实际问题，关键是找出两个相等关系，然后将相等关系用方程表示出来。

考点3 解二元一次方程

例3 （2018·宿迁）解方程组：

【解析】由①，得x=-2y。③

把③代入②，得

3×（-2y）+4y=6。

解得y=-3。

把y=-3代入③，得x=6。

【点评】解二元一次方程组的关键是消元，具体求解时要根据方程组的特点选择恰当的方法消元。本题第一个方程中x的系数为1，用代入消元法求解较为方便。

考点4 整体思想

【解析】仔细观察两个方程组，我们发现如果把a+b，a-b分别看成一个整体，那么第二个方程组中的a+b、a-b分别相当于第一个方程组中的x、y。因为第一个方程组的解为即为第二个方程组的解。

【点评】利用整体思想，可建立某些特殊方程组的解之间的关系。

考点5 列方程组解应用题

例5 （2018·黄冈）在端午节来临之际，某商店订购了A型和B型两种粽子，A型粽子28元/千克，B型粽子24元/千克。若B型粽子的数量比A型粽子的2倍少20千克，购进两种粽子共用了2 560元，求两种型号粽子各多少千克。

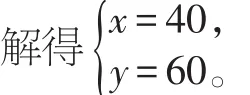
答：订购了A型粽子40千克，B型粽子60千克。

【点评】列二元一次方程组解应用题，简单的问题可直接由相等关系列出方程组，复杂的问题可利用列表法或线段图等找到相等关系，进而再列方程组求解。

考点6 新定义试题

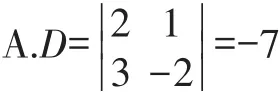
B.Dx=-14

C.Dy=27

【点评】解答新定义试题时，关键是理解新定义的意义，进而在此基础上求解相关问题。