基于GeoGebra的任务型信息化教学方案设计——以《一次函数的图像和性质》课程为例

杨冬梅，郑梦菲

(1.云南师范大学信息学院，云南昆明650500；2.广西师范大学教育学部，广西桂林541006)

21世纪是信息化的时代，各类科学技术融入学校教育教学，如何有效高效培养学生创造力、批判性思维、问题解决能力等问题成为学校教育教学的重点问题，将技术—教学法—内容知识(TPACK)的模式框架与21世纪技能的一些教学要求相匹配，是现在研究的重点方向[1]。数学本身是一门很美且与日常生活密切相关的学科，但是很多学生从小便害怕和厌倦数学，觉得数学知识枯燥难懂，数学新课标指出，学习数学的重要方式是化抽象为形象，动手实践，主动探索，合作讨论。利用GeoGebra数学技术软件与任务型教学相结合，以八年级上册《一次函数的图像和性质》课程为例，进行其在初中数学学科中教学方案的设计，通过任务布置，引导学生主动利用GeoGebra软件探索一次函数的图形特征和性质，将自我探究与小组合作讨论想结合，以提高学生的学习热情，让学生体会发现知识的乐趣，加深对知识的理解和记忆，培养其创造力和思考力。

1 概念介绍

1.1 GeoGebra数学软件

GeoGebra(Geometry+AlgeBra)是2002年由美国佛罗里达州亚特兰大学的Markus Hohenwarter教授所设计的一款结合几何、代数和微积分的免费动态数学软件[2]。该款软件在国外应用较为普遍，近年来，在我国也逐渐开始推广和应用，特别是在其强大功能与具体数学学科知识相整合方面，受到了越来越多的关注。通过高校带动中小学的模式，越来越多的中小学老师已经把它应用于真实的教学环境中，给数学教学带来新的生机和活力。

1.2 任务型教学

任务型教学是指围绕着知识内容为中心的任务设计、实施和完成的过程，强调的是真实的实践性[3]。任务型教学最初是从“做中学”衍生而来，方法结构越来越完整和系统化，逐渐扩展到越来越多的学科领域，为各个学科带来了新的启发和研究方向。在本文中首先通过对学习内容、目标等的分析，结合GeoGebra软件设计学生学习的任务过程，利用任务来驱动学生主动思考和探索，旨在培养学生的兴趣，增强学生解决问题的能力。

2 理论基础

2.1 数字化环境下的教学设计理论

信息化教学设计是以设计“问题”情境以及促进学生解决问题的教学策略为核心的教学规划与准备过程[4]，并且能利用信息化的手段和环境辅助教学，设计出既能满足学生知识需求又能同时培养学生的创新能力、问题解决能力和协作精神等品质的方案。2018年颁布的《教育信息化2.0》中提出的任务之一是：“持续推动信息技术与教育深度融合，促进两个方面水平提高[5]，”可见教育的发展已离不开信息技术的发展。在本研究中，以GeoGebra软件为载体，设计任务型信息化教学方案。

2.2 任务分析理论

任务分析理论是指在教学活动开始之前，对学习内容和学习目标等因素进行分析，找出学习者的现状与教学目标之间的差距和缩短差距所需的必要条件，并根据现有的教学条件，选择合适的教学策略和手段，设计合理的教学活动方案，以实现教学目标，完成教学任务。在本案例教学方案设计中，根据一次函数的内容和目标分析，重点设计一次函数中参数意义的探究任务，归纳总结一次函数的图像性质和规律，让学生在任务探究中进行学习和成长。

3 基于软件工具GeoGebra的任务型教学方案设计

3.1 教学分析

3.1.1 学习内容分析

本课程内容是九年义务教育初中数学人教版八年级上册第十二章第二小节《一次函数》的重要知识点，是在学习了平面直角坐标系中点的坐标及图形的平移变换规律基础上数与代数内容的函数部分，为接下来反比例函数和二次函数的学习奠定了基础。GeoGebra软件具有强大的功能，涵盖了初中数学中的代数、几何和概率统计等方面内容[6]。借助GeoGebra软件对一次函数图象及性质内容作出动态效果，让学生可以自已动手探索，通过“做中学，玩中学”使学生对一次函数图像和性质掌握得更好，理解得更透。

3.1.2 教学目标分析

1、知识与技能

(1)理解参数k、b的意义。

(2)会画一次函数的图像，增强作图能力。

(3)总结和归纳一次函数的性质，掌握一次函数的性质，能结合图像说出一次函数的性质。

2、过程与方法

通过完成任务式的探索，使学生经历用GeoGebra作出一次函数的图像，观察参数k、b对函数图像变化的影响，能够做到数形结合，真正理解函数的性质。

3、情感态度价值观

通过GeoGebra作y=kx+b的图像，并且使图随k、b参数变化而变换图像，让学生逐步形成观察、分析并解决问题的能力，逐步形成积极探索和合作的优秀品质。

3.1.3 教学重难点

1、重点：(1)总结正比例函数的图像特征。(2)探索一次函数的性质及其图像特征。

2、难点：结合图像理解一次函数的性质的过程?。

3.2 教学过程

任务探究：学生动手操作GeoGebra，画出y=kx+b的图像(见图1)。通过拖动GeoGebra软件上设置的k参数和b参数的滑动杆，改变k值和b值。观察图像变化情况和发现其中规律，完成表格的填写。

学生操作：学生分组完成完成操作，把对应图像特征情况进行记录，见表1。

分析表格：记录操作数据，并提出以下问题。

(1)当b不变，k>0时，函数图像有何特征？当b不变，k<0时，函数图像有何特征？

(2)k值代表的意义是什么？b值代表的意义是什么？

小组汇报：

(1)各小组派代表在课堂上向全班同学展示本小组的任务探究结果，并亲手用GeoGebra软件进行演示，解释原理。

(2)各个小组的其他成员记录其他各组的结果，并对本小组的探究展示过程进行自评。对成果进行组间互评，最后由老师进行点评和总结。各小组取长补短，共同进步。

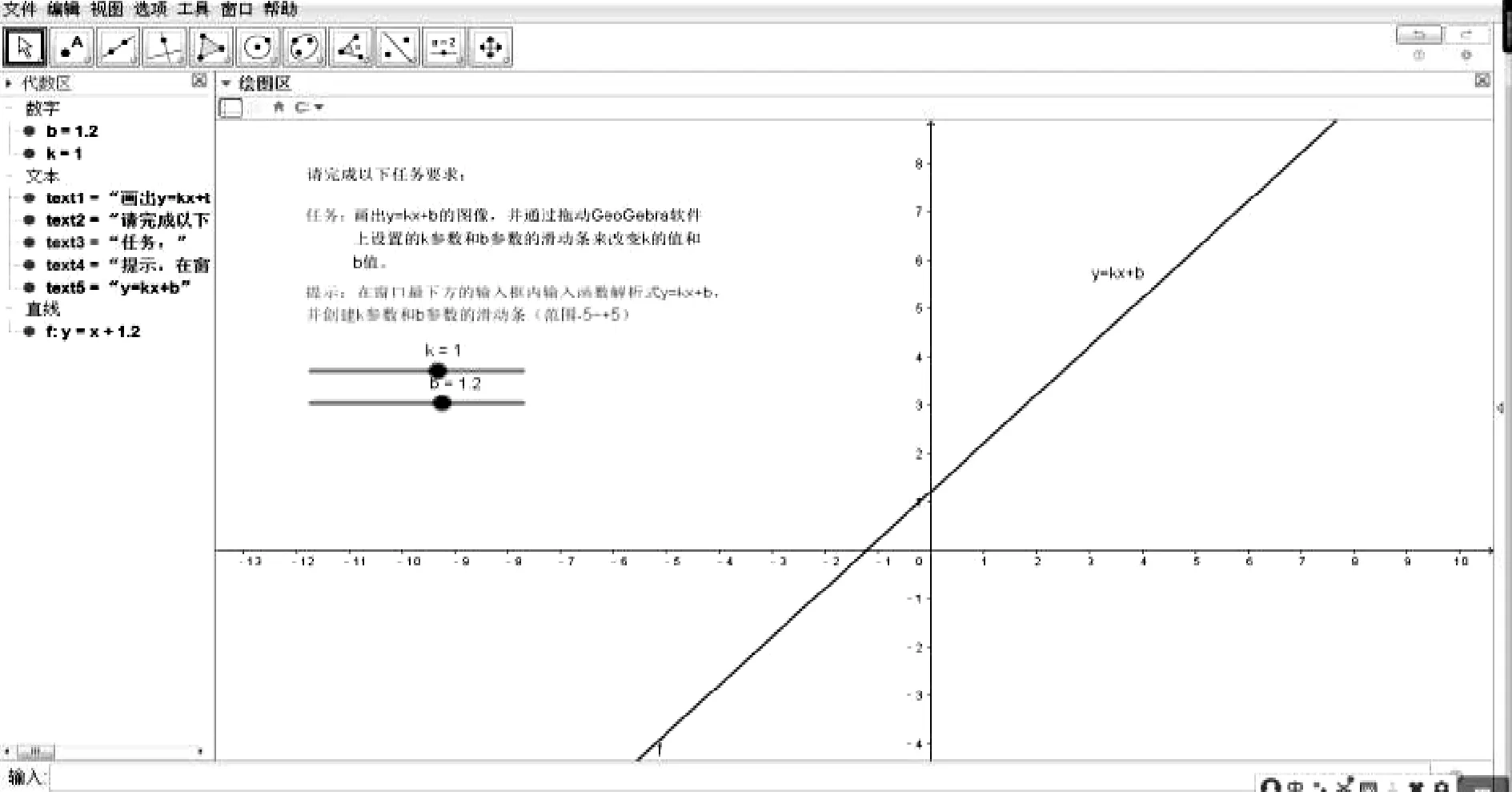
图1 y=kx+b图像

表1 图像特征记录

教师小结：k值决定直线上升、下降的趋势。当k>0，函数图像递增，y随x的增大而增大；当k<0，函数图像递增，y随x的增大而减小。b值决定直线与y轴交点的位置为(0,b)，当b>0时，直线与y轴交于x轴以上；当b>0时，直线与y轴交于x轴以下。

4 结语

本方案设计利用GeoGebra让学生任务向导，自己动手操作，发现一次函数的图像特征及其性质，基本达到新课标规定的要求。另外，通过学生自我探索和思考，利用小组合作讨论汇报的方式，锻炼了学生的数学逻辑思维能力、小组协作能力、空间想象能力及发散性思维，帮助学生成为知识的主动获取者。但是该方案仅在设计阶段，还未在课堂上实施，可能会出现很多不可控的因素，例如上课时间的把控性不够强、学生因对教学设备的好奇而分散注意力等。在实际应用中可通过不断发现问题并进行改进，该方案将不断趋于完善。以学生为主体，教师为主导，借助GeoGebra，进行任务型信息化教学，是对信息技术与教育深度融合的实践。