基于分段三次Hermite插值的光源相关色温及色偏差的快速计算

宋喜佳，冯学妮，郝亚茹，邓招奇

(1.电子科技大学中山学院计算机学院，广东 中山 528402；2.中山市启航技工学校，广东 中山 528402)

引言

黑体辐射源的色温是黑体的绝对温度。如果一个光源发射光的颜色(即光色，又称色品)与某一温度下的黑体发射光的颜色相同，那么此时黑体的绝对温度值就叫做该光源的颜色温度(简称色温)。当光源的光色与某一温度下的黑体辐射光源光色最为接近时，后者的色温即为光源的相关色温[1，2]。相关色温是照明光源的重要参数，不仅决定了人眼视觉观察到的“白光”颜色种类，还对人体的昼夜节律、体温调节以及热平衡等非视觉生物现象产生重要影响[3]。

照明光源的另一个重要参数是Duv，它描述了待测光源色坐标偏离普朗克黑体辐射轨迹的距离和偏离方向。当Duv的数值过大时，说明光源光色偏离太远，人眼会观察到发黄、发绿或者发紫等情况[4]。Duv的计算公式为

(1)

其中(uc,vc)是待测光源的CIE 1960 UCS色度坐标，(u0,v0)是普朗克黑体轨迹上距离(uc,vc)最近的点的CIE 1960 UCS色度坐标。

传统的色温计算方法主要包括直接内插法、三角形垂足法、曲线拟合法等[4-10]。直接内插法和三角形垂足法尽管计算精度相对较高，但是为了确定与待测光源色坐标(u,v)最近的两条等色温线，需要逐次搜索比较，计算量大、耗时较长，并且直接内插法不能同时给出相关色温和Duv的值。求解相关色温的其他方法，如逐次逼近法、多项式逼近法、曲线拟合法等，尽管不需要逐次比较，计算时间较快，但是适用的色温范围十分有限，计算精度也不够理想。

1 计算相关色温的三次Hermite插值算法

1.1 确定黑体辐射轨迹上温度Ti与CIE 1960 UCS色坐标(ui,vi)的对应关系

第一步，对温度T进行离散化，得到T的离散列表。本文离散化的方法参考文献[4]的做法，在1 000～20 000 K的色温范围内，对T进行1%步进离散化，分别为

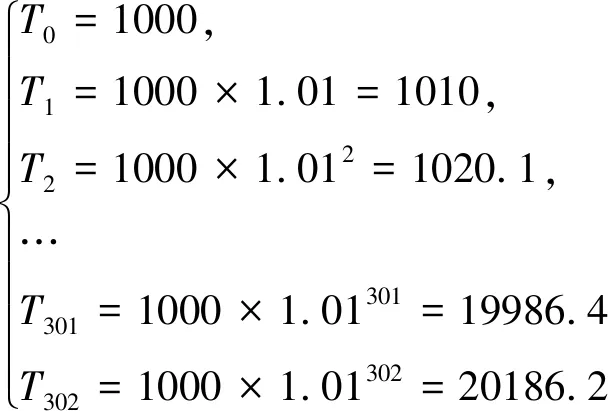
(2)

第二步，依据普朗克黑体辐射定律，计算离散温度点Ti(i=0～302)对应的黑体辐射光谱功率分布。

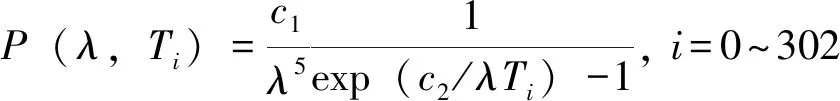
(3)

这里，c1是第一辐射常数，c1=2πhc2；h是普朗克常数，c为光速；c2是第二辐射常数，c2=hc/k；k为波尔兹曼常数。

第三步，依据黑体辐射的光谱功率分布，计算其颜色三刺激值。

(4)

第四步，计算黑体辐射在温度Ti(i=0～302)时对应的CIE 1960 UCS色坐标(ui,vi)。

(5)

第五步，将温度Ti(i=0～302)与色坐标(ui,vi)，按照两者对应关系形成表1。

表1 温度与CIE 1960 UCS色坐标的对应关系Table 1 The relationship of temperature and chromatic coordinate in CIE 1960 UCS

1.2 计算黑体辐射轨迹在各离散温度点Ti的曲线斜率li

相应的曲线斜率为

(6)

这里，Xi,Yi,Zi是黑体在温度Ti时的颜色三刺激值，Xi′,Yi′,Zi′是颜色三刺激值对于温度Ti的导数，计算方法如下：

(7)

这里，PT′(λ,T)是P(λ,T)对T的偏导数：

(8)

按前面所述过程，计算各Ti(i=0～302)对应的li，然后将li加入到表1中，得到表2和图1。

表2 黑体轨迹上温度、CIE 1960 UCS色坐标以及斜率的对应关系Table 2 The relationship of T,chromatic coordinate in CIE 1960 UCS and slope on the Planck blackbody locus

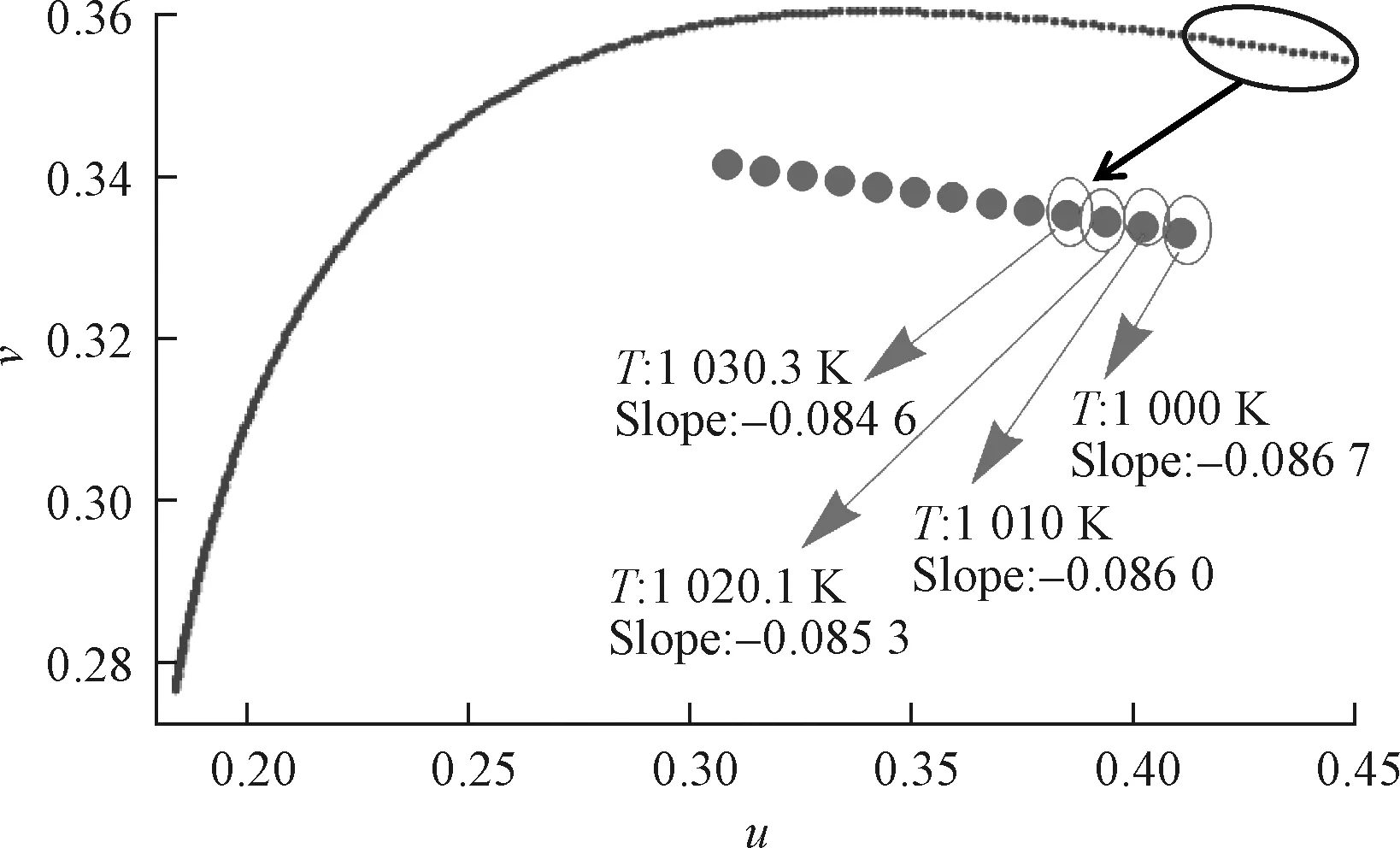
图1 黑体轨迹上温度、CIE 1960 UCS色坐标以及斜率的对应关系Fig.1 The relationship of T,chromatic coordinate in CIE 1960 UCS and slope on the Planck blackbody locus

表1、表2数据只需要计算一次，本文后继步骤可以直接调用这些数据，不用重复计算。

1.3 基于分段三次Hermite插值方法描述黑体轨迹

在区间[u0,u302]上，定义一组分段三次插值基函数αj(u)及βj(u)，这里j=0,1,…,302，则黑体轨迹方程v(u)可表示为

(9)

其中基函数αj(u)表示为

(10)

βj(u)分别表示为

βj(u)=

(11)

按照上面公式，分别在区间[u0,u1]、[u1,u2]、…、[u301,u302]计算v0(u)、v1(u)、…、v301(u)，即

(12)

将求得的各多项式系数，以及前面获得的温度值、色坐标、斜率统一存于表3。

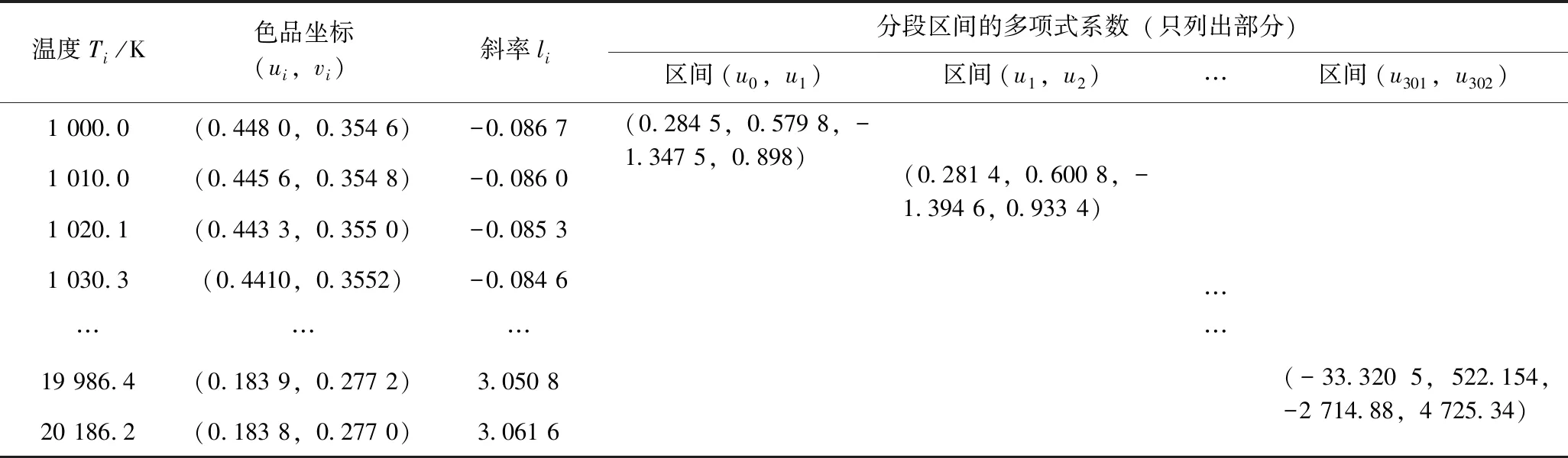
表3 黑体轨迹上温度、CIE 1960 UCS色坐标、斜率以及多项式系数的对应关系Table 3 The Relationship of T,Chromatic Coordinate in CIE 1960 UCS,Slope,and multinomial coefficient on the Planck Blackbody Locus

借助计算机和现代数学软件(如Mathematica)，可以通过编程快速获得上述各分段函数。

1.4 确定黑体轨迹上距离待测光源(uc,vc)最近的坐标点(u0,v0)

假设已知待测光源的光谱功率分布，因此可求得待测光源的色坐标待测光源(uc,vc)(本文直接认为(uc,vc)是已知量)，故点(uc,vc)到普朗克黑体轨迹v(u)的距离d(u)可按照如下方法获得：

(13)

假设当(u,v)=(u0,v0)时，d(u)的一阶导数d′(u)、二阶导数d″(u)分别满足：

(14)

则d(u)取得最小值d(u0)。另外，按照Duv的定义，有

Duv=d(u0)sgn(vc-v0)

(15)

1.5 确定黑体轨迹上某点(已知其色坐标)对应的色温

在求出黑体轨迹上距离待测光源(uc,vc)最近点色坐标(u0,v0)以后，下一步是确定(u0,v0)所对应的色温T0，通常有多种方法，如McCamy近似公式、Hernández-Andrés近似公式等，本文采用三角几何近似的方法来确定T0(图2)。最后，根据相关色温的定义可知，该待测光源的相关色温Tc为Tc=T0，则

(16)

由于黑体轨迹采样点较密集时(如本文采用的1%步进采样)，θ1、θ2均较小，因此式(16)可以近似为

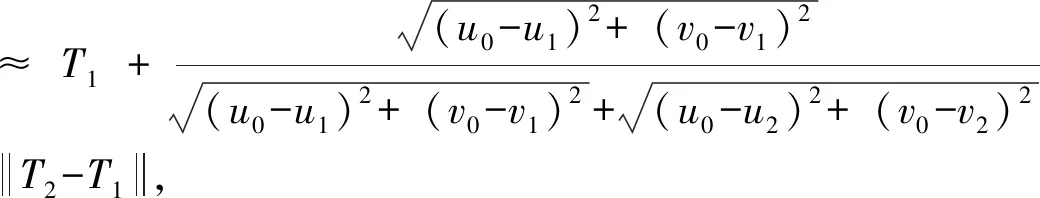
(17)

图2 利用三角几何近似法确定相关色温Fig.2 Calculate CCT based on the trigonometry approximate method

2 实验与测试结果

2.1 计算并验证“标准黑体轨迹等温线色度坐标表”的相关色温及计算误差

依据参考文献[1，2]中提供的“标准黑体轨迹等温线色度坐标表”，使用本文算法，由各色度坐标计算相关色温，并与标准值相比较，相对误差以及Duv如表4和图3所示。

从图3可知，高色温区误差稍微偏大，其原因如下：对温度进行1%步进离散化，在高色温区步长间隔变大，导致数据误差变大。采用1%步进离散化的好处是，实际照明光源多工作在暖光、正白区域，冷光源色温一般也很少超过7 000 K，该方法可保证在光源比较重要的低色温、中色温区域获得相对更加精确的计算结果，同时数据量不至于太大。

2.3 标准色温灯的相关色温计算

标准色温灯的光电参数如表5所示。利用远方HAAS-2000光谱仪对该标准灯进行测量，得到的该标准灯的光谱功率分布如图4所示。使用HAAS-2000光谱仪对标准色温灯的相关色温进行测量，测量结果与计算结果如表6所示。

表4 “标准黑体轨迹等温线色度坐标表”的计算结果与计算误差Table 4 The Calculation Result and Calculation Error of “Standard Chromatic Coordinate Table for The Isothermal Lines of Blackbody Locus”

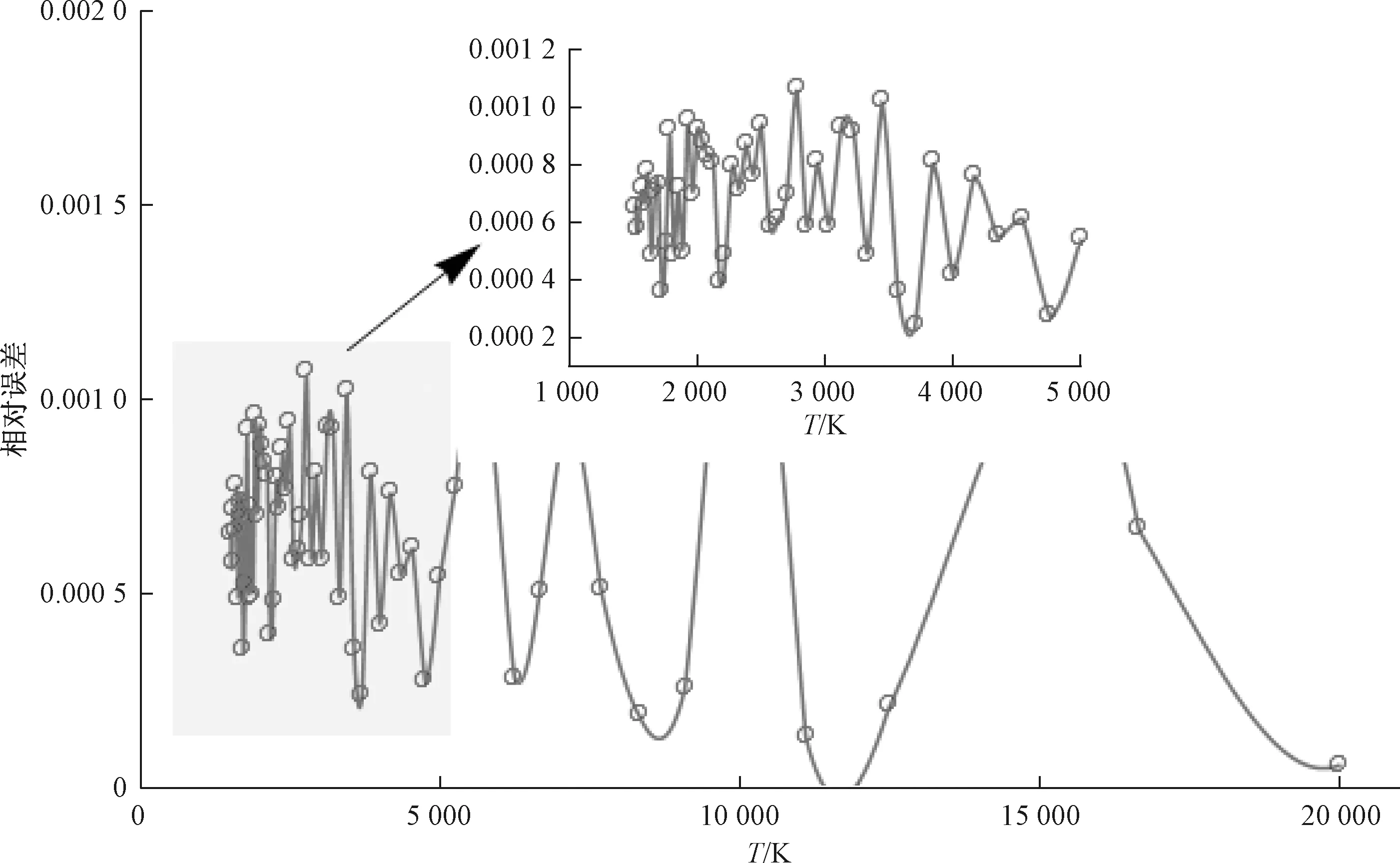
图3 “标准黑体轨迹等温线色度坐标表”的相关色温计算结果与计算误差Fig.3 The calculation result of CCT and calculation error of “standard chromatic coordinate table for the isothermal lines of blackbody locus”

表5 标准色温灯的主要参数Table 5 The main parameters of the colour temperature standard lamp

图4 标准色温灯的相对光谱功率分布Fig.4 Relative spectral power distribution of the colour temperature standard lamp

表6 标准色温灯的相关色温、色温相对误差及Duv的对比Table 6 The comparison of correlated color temperature,color temperature and Duvof the color temperature standard lamp

3 总结

经过推导计算，我们确定了普朗克黑体辐射轨迹上温度Ti、色坐标(ui,vi)以及曲线斜率li三者之间的对应关系，建立了可以精确平滑地描述普朗克黑体辐射轨迹的分段三次Hermite插值函数(此过程过程只需计算一遍，然后将计算的结果存储起来，后续计算可以直接调用，有利于提高计算效率)；在此基础上，利用解析方法快速计算待测光源(uc,vc)与普朗克黑体辐射轨迹上的最近点的色坐标(u0,v0)以及二者之间的距离d(u0)，避免了传统算法需要逐步搜索比较的烦冗耗时；最后，采用三角几何近似的方法，确定色坐标(u0,v0)的色温T0，得到待测光源(uc,vc)的相关色温Tc。通过对“标准黑体轨迹等温线色度坐标表”和“标准色温灯”的仿真计算以及实测，本文算法的相对误差基本稳定在10-4范围内(需要注意的是，由于温度采用1%步进进行离散化，在高色温区的误差波动相对较大)。因此本文算法在实现快速计算相关色温的同时，还具有比传统计算方法更好的计算精度，适用色温范围广(1 000～20 000 K)的特点，可以应用在光源色温计算、光谱优化等方面。