Platoon架构下VANETs车间通信过程及性能分析*

郭红叶,赵 海,司帅宗,彭海霞

(东北大学 计算机科学与工程学院,辽宁 沈阳 110819)

为了解决高速公路上车流密集以及由之带来的交通拥堵、交通事故多发等问题,有发达国家提出了智能交通系统(intelligent traffic system,简称ITS)的概念,旨在将信息、通信和控制等技术应用于交通管理,实现车辆的智能驾驶,道路的高效利用.而最初为自动高速公路系统(automated highway systems,简称 AHS)提出的 platoon车辆编组成为近几年研究的热点.Platoon架构是由若干智能驾驶车辆按照一定几何队形组成的车队,通过车载雷达等传感器和车间无线通信实现以恒定间距稳定地跟随前方车辆,车队成员通常具有相同目的地,且行驶速度较普通车辆要快,车间间距可以达到很小(几米),故而有效提高了道路容量,而特殊的编组协同驾驶有助于减少空气阻力、节约燃料,提高道路安全性.Platoon系统稳定运行的关键在于车载智能控制系统对platoon中车辆成员的加速/减速和变道等驾驶行为的实时控制,以保证车辆的运动状态误差不沿纵向方向放大,即满足队列稳定性[1].而控制策略的准确实施由车辆间的有效实时通信来保证.车载环境下的通信网络称为车载自组织网络(vehicular Ad Hoc networks,简称 VANETs),包括车车通信(IVC/V2V)和路车通信(RVC/V2I).通信网络采用DSRC/WAVE协议架构,即专用短程通信技术(dedicated short range communication,简称DSRC)和车载环境中的无线接入(wireless access in vehicular environment,简称WAVE)标准,在物理层和MAC层采用适用于高速车载环境的IEEE 802.11p协议标准.而DSRC采用IEEE 1609.4作为对MAC层的改进,增加了多信道切换功能[2].

关于车载自组网通信协议和通信技术的研究大多基于普通驾驶车辆,其存在通信距离远、路由困难、通信链路不稳定且网络拓扑高度动态变化的问题[3].大量研究主要是对上述问题进行改进,从而探讨通信节点间的路由算法、MAC层接入技术以及物理层技术等等[4-7].而将道路上的车辆组成稳定platoon编组的形式能够有效地改善VANETs通信网络的连通性[8],保证platoon中传递信息时效性和可靠性的车间无线通信会显著影响整个车辆编组的协调控制和安全行驶,但是车载环境下不稳定的通信信道、复杂的道路环境和车辆节点的高速运动都会影响信息的有效实时传输,从而将包投递延时、误码、丢包等不确定性引入到platoon的控制系统中.所以有必要对 platoon中车辆之间的通信过程及通信网络性能进行分析,但到目前为止仍然没有较全面的相关理论研究.现有研究platoon系统的相关工作对车间通信过程的处理方法大致可以分为以下几类:假定车辆间通信近似理想,设置通信性能度量为典型分布,仅考虑车辆编组中成员通信失败的情况对platoon的控制模型和协作管理策略造成的影响或者通过platoon控制指标和运行条件评估相应的通信网络性能阈值.

有相当一部分文献都不考虑通信过程的不确定影响,将车间通信设定为理想状态,即假定车载控制系统能够实时、准确地获取到所需的全部信息[9,10].但是车辆间传递信息的丢包现象和延时等通信网络特性对车辆的协调和控制具有非常显著的影响.Ploeg等人虽然在设计基于不同信息流拓扑的 CACC(cooperative adaptive cruise control)控制器时考虑了通信延时,但是所有车辆的延时都相同且为固定值[11].而实际通信网络的时延等特性是可变的,这种不确定性会对控制因子等产生不同程度的影响,从而破坏 platoon的队列稳定性[12],很多学者考虑到车辆间不容忽视的通信状况,将呈不同分布的通信参量加入到platoon的控制研究中.Guo等人考虑了VANETs网络容量限制和通信数据包的随机丢包概率满足伯努利分布的情况,提出通信网络接入调度和platoon控制联合设计的算法[13].Segata等人同样基于通信信标遭遇伯努利分布随机损失的情形来研究platoon车间协调策略[14],但在实际场景下,丢包率是由通信机制和信道状况等共同决定的,并不是随机分布的,而且上述文献均未考虑通信延时.Bernardo等人提出在platoon协调控制问题建模时引入呈随机分段函数的可变通信延时,其下界为0,上界低于典型IEEE 802.11p车载网络的平均端到端延时(数量级为10–2s)[15,16].但车辆的通信延时不太可能表现为一种规则的分布,而且这种延时无法用来改进通信算法.Amoozadeh等人在研究基于VANETs的platoon上层管理协议时,仅讨论了信息更新时间间隔内未接收到信标信息导致通信失败的情况[17].除此之外,更多的文献集中在研究 platoon控制策略或者运行性能时估计或仿真通信网络性能阈值.Xu等人在研究信息获取方式和内容对platoon避免车辆追尾碰撞安全性的影响时,推导了安全距离下的最大容忍通信延时[18].但是文献中设定的 platoon车间间距太大,故而导出的通信延时和实际情况相差甚远.Shao等人在设计platoon的VANETs网络MAC层协议时采用多优先级马尔可夫模型推导了基于连通概率的网络饱和吞吐量[19].但他们并没有对通信延时和丢包概率给出相应的分析.Fernandes等人在车辆间的信息更新算法中,通过网络仿真软件得到典型场景的延时分布[20].虽然能够得到较为准确的通信性能度量的数值,但却没有相应理论上的研究,也无法从算法上改进车间通信性能.Du等人基于确定路段间断性多跳数据传输以及车辆运动状态导致的动态交通流,推导了车载环境下通信网络中的数据传输延时[21].但是网络中的车辆并不是 platoon编组的形式.Jia等人基于4-D Markov模型建模考虑信道条件的CSMA/CA退避过程,通过加入数据帧单位块的数量、数据处于发送还是转发状态这两个变量,对2-D Markov模型进行了改进,推导了网络饱和吞吐量和传输延时[22].Jia等人此项工作的不足之处在于假设的通信网络流量是饱和的,且仅研究车辆向路边单元传输信息的上行链路,而没有考虑platoon内部车间通信的丢包现象.

上述多数工作对于 platoon交通流场景下的车间通信模型和网络性能的处理方法太过理想或考虑不够全面,而且鲜有文献专门对platoon架构下车辆间的通信过程以及通信延时和丢包概率等通信性能进行理论研究,定量地推导platoon编组中车辆间传递信息的通信不确定性度量指标.从而从车辆的有效通信角度入手,通过控制协同策略和通信机制来减弱不稳定通信对platoon构建和运行的影响,提高 platoon架构的安全性和稳定性.针对现有研究工作中的缺陷,本文提出一种 platoon架构下智能车辆间通信的网络性能分析方法,其中,车车通信依靠专用短程通信(DSRC)技术实现,且在分析数据包传输过程时,除了争用信道的退避阶段外,还分析了数据包在 MAC层缓冲区的排队过程以及两者间的联系.本文的通信模型设定缓冲区长度有限,信道存在干扰误码现象,且可能没有数据包到达网络,故而所研究的车间通信更接近实际的车载环境.文中分别对 platoon组内车间通信和多个 platoons组间通信进行了分析,并且在后者的分析中区分了处于车队不同位置处的车辆特性.最终得到 platoon编组关键参数及通信网络相关参数对数据包传输总延时和包丢失概率等通信性能度量的影响,同时验证了DSRC技术支持的车间通信的端到端延时可以满足platoon编组干扰不放大的队列稳定性需求.

本文第1节介绍platoon智能车辆编组系统的组成及成员车辆间的通信机制.第2节给出platoon组内车间通信过程及性能分析方法.第3节给出platoons组间通信过程及性能分析方法.第4节对提出的分析方法进行数值仿真及可行性验证.第5节是本文的总结.

1 Platoon智能车辆编组系统

1.1 Platoon系统结构

Platoon中担任不同角色的车辆在队列的组建和运行过程中负责不同的功能.Platoon系统结构如图1所示,其中,领导车辆(leader vehicle)是整个platoon的管理者,主要负责:存储和管理platoon配置信息,比如成员目的地信息、platoon ID、platoon成员数量等;为其他车辆传递控制信息并且收集成员车辆的状态信息;协调编组中车辆的动态加入或退出、platoon编组的分离和融合等操作.跟随车辆(follower vehicle)负责向领导车辆发送加入、退出和变道请求,得到确认信标后即可完成相应操作;在车载控制系统的协调下保持以期望间距和速度跟随前方车辆.而且跟随车辆可以在到达目的地或者完成信息获取后随时离开,而不会影响整个 platoon的正常运行.队尾车辆(tail vehicle)主要负责道路上不同platoon编组之间的信息传输,即和下一个platoon智能车队的领导车辆通信.在道路上行驶的其他车辆分为普通车辆和free agent,后者一般具有成为platoon成员的必要设备,比如车载协同控制器,可以在感知到合适的platoon编组靠近时,向该车队领导车辆发送请求,加入该车队.

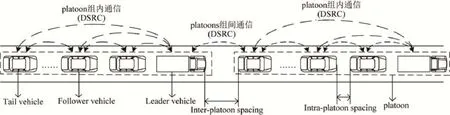
Fig.1 The system structure of platoon图1 Platoon系统结构

Platoon系统的参数包括platoon组内车间距(intra-platoon spacing)、platoon组间间距(inter-platoon spacing)和platoon成员数量(platoon size)[23].Intra-platoon spacing由车载自适应控制系统设定,其最小值应保证车辆不发生碰撞,最大值低于通信网络限定的信息有效投递范围,保证编组内部的连通性.Inter-platoon spacing是两个相邻 platoons之间的距离,一般由前方队列中的队尾车辆和后方队列中的领导车辆界定,该值应能保证当后一个 platoon编组感知到前方 platoon的减速或车辆变道等事件后,有足够的时间调整自身状态,避免发生碰撞.Platoon的队列稳定性要求干扰沿着车辆队列传播时是衰减的,所以设置间距时不仅要考虑道路上的车辆容量，还要不违背platoon系统对干扰的鲁棒性.Platoon成员数量随着车辆动态加入或退出而不断发生变化,其上界是保证组内单跳通信连通性和队列稳定性的最低要求.

Platoon系统中的车辆之间通过无线通信传递速度、加速度以及驾驶行为等信息,将其输入到车载自适应控制系统后,通过控制协调算法得到当前车辆期望的加速度,从而控制车辆的加/减速维持和前方车辆的期望间距和期望的速度.下面是针对车辆控制增益和间距参数相同的均匀platoon的线性增益控制算法[13]:

其中,i是车辆的编号,若platoon中车辆数量为n,则i∈[0,n–1],领导车辆编号为0;ui(t)是车辆控制器的输出期望加速度,ke(t)是车辆间距误差控制增益,h是间距控制策略设定的车间恒定时间间距;vi–1(t)、ai–1(t)、kv(t)和ka(t)分别表示当前车和前方相邻车的速度差、加速度差以及相应的控制增益;v0(t)、a0(t)、kv0(t)和ka0(t)分别表示当前车和领导车辆的加速度差、速度差以及控制增益.vi–1(t)、ai–1(t)、v0(t)和a0(t)即为车间无线通信传输的实时信息.

1.2 Platoon通信机制

车载自组织网络采用专用短程通信(DSRC)技术支持车辆间通信以及车辆与路边基站之间的通信,该技术工作在5.9GHz频段,包括1个控制信道(CCH)和7个服务信道(SCH),带宽均为10Hz.控制信道传递安全信息和控制信息,其他非安全信息或者娱乐信息在服务信道中传输,DSRC技术的高数据速率和 100m～1000m的传输范围等特性适合platoon架构中车辆的信息传播和共享.道路上多个platoons之间的通信过程包括platoon内部成员间的通信和不同platoons组间的通信.前者一般通过单跳实现,通信站点为platoon内部所有成员车辆;而后者可以通过单跳或者多跳实现,由每个platoon的领导车辆和队尾车辆负责信息传递.两种通信的信息交换在不同服务信道上实现,这种信道的协调和标定在控制信道时隙广播给成员车辆.

本文主要研究platoon编组架构下基于IEEE 802.11p协议的车间通信网络传输延时和包丢失概率等MAC层性能,将通信过程分为缓冲队列的排队阶段和争用信道资源的传输阶段.接入机制采用 RTS/CTS(request to send/clear to send)握手机制,有效减少了阻塞间隔.MAC层服务的基础是分布式协调功能(DCF)接入方式,DCF基于冲突避免的载波检测多路访问(carrier sense multiple access with collision avoidance,简称CSMA/CA)机制,使用二进制指数退避算法避免冲突.发送数据包前先确定信道空闲并持续 DIFS时间再发送,若信道忙,则从[0～CWi]中选择随机退避时间等待信道空闲,其中,CWi=2iCWmin,CWi代表竞争窗口值,与传输失败次数和退避阶数有关,i是退避阶数.当达到最大退避次数时,数据传输成功或者达到最大重传限制都将回到CWmin,退避计数器在每个信道空闲时隙都会减1,若信道忙,则计数器停止计数.当退避计数器值减为0时,开始发送数据.

2 Platoon组内车间通信

本节对platoon编组内部的车间通信过程及通信性能进行分析,参与通信的车辆为platoon组内所有成员车辆,每辆车的通信性能相同.

2.1 组内通信的退避过程

本文所研究的通信过程的无线信道是非理想的,即在信道中传输的数据包可能出现误码,且车辆站点并不总是有数据包发送,此时网络处于非饱和流量状态,这里用通信系统处于空闲状态来表示这种情况.当缓冲队列为空且没有新的数据包到达时,系统进入空闲等待状态,等到需要发送数据时,再开始竞争信道资源.车辆在通信过程中数据包传输失败可能是因为网络中多辆车同时发送信息出现信道阻塞,也可能是不稳定的无线信道受到干扰导致了误码.假设最大重传次数为M,最大退避阶数为M′,若数据包重新发送次数达到M+1次时仍然传输失败,则认为数据包丢失.设车载环境中的信道比特误码率为perror,传输一帧数据的总比特数包括物理层和MAC层头部信息、有效数据长度以及握手机制的数据开销等.故传输数据帧出错的概率可以计算为

在二维Markov过程{s(t),b(t)}中加入系统空闲的情况,其中,s(t)和b(t)代表在时隙t内退避状态和退避计数器取值的随机变量.车辆在任何一个时隙由于发生误码和信道阻塞数据包传递失败的概率pm以及发送数据包的概率p可推导为

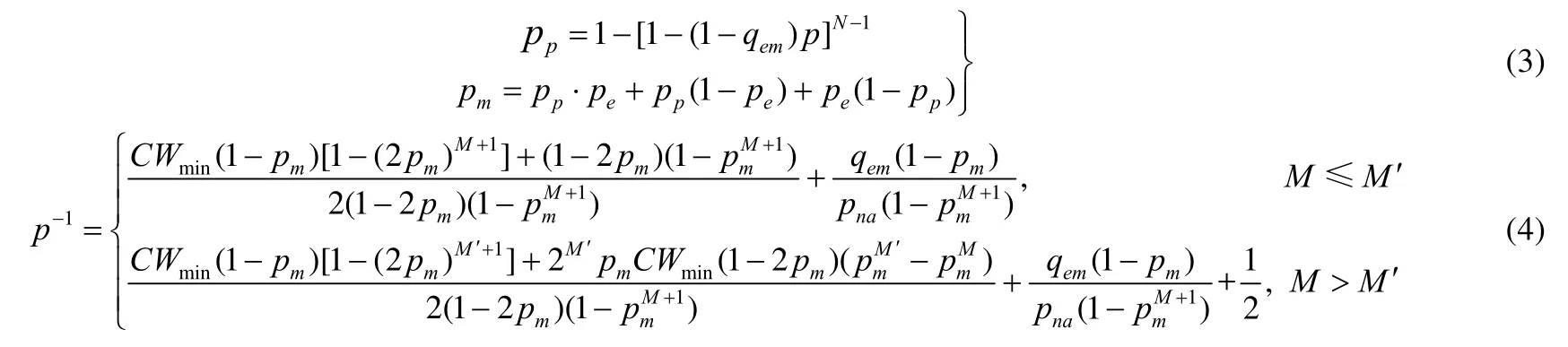
其中,pp代表某一时隙超过一辆车发送信息使得信道发生阻塞的概率,N是 platoon成员数量.pna是新数据包的到达概率,qem代表MAC层缓冲队列为空的概率,即车辆没有数据包发送的可能性大小.

2.2 组内通信MAC层排队过程

Platoon编组中的车辆向其他成员传递信息进入 MAC层时,多个数据包首先在缓存队列中排队等待,到达队列头部时再侦听信道获取通信资源的使用权.而由于实际情况中车辆传输数据包的时刻和数量是无法预知的,可以将该行为看作是随机事件,故由概率性可知,车辆节点在某时刻发送数据包的次数服从参数为λ的泊松分布,λ表示单位时间内到达的数据包个数.数据包在排队系统中满足先进先出的原则,即先到达的先被服务.排队过程用M/G/1/K模型来近似[24,25],排队队列的长度有限,当缓存队列满队时,无法继续接收数据包.排队系统在某时刻的状态表示为信道被占用时缓存队列中的数据包数目,设定MAC层的缓存队列存放数据包的上限为K.为了得到排队系统的稳定状态概率,需要先计算 MAC层的服务时间分布,数据包服务时间表示为从排队结束争用信道资源开始到传输成功或者达到最大重传次数为止的时间[26],一般设定为空闲时隙τ的整数倍.假设取不同倍数的概率分布为,其中,T表示倍数,且T∈[0,Tm],则最大服务时间表示为Tmτ.用一维变量X(t)来描述排队系统的状态,X(t)是在完成排队的数据包离开时,排队系统中剩余的数据包个数,缓存队列在第j个数据包离开排队系统时刻之前所处状态的分布可以用无记忆的嵌入式马尔可夫链建模.故而在一个服务时间内有k个数据包到达的概率表示为

其中,Ts、Te分别表示数据包发送成功所需要的时间和由于信道误码传输失败所经历的时间,可以表示为Ts=Te=DIFS+RTS+SIFS+CTS+ SIFS+Hphy+Hmac+l+SIFS+ACK,而Tc表示与其他车辆的数据包发生冲突时占用通信资源的时间,表示为Tc=DIFS+RTS+SIFS+CTS.

处于排队等待状态的剩余数据包数量X(t)的排队系统稳态概率分布可推导为

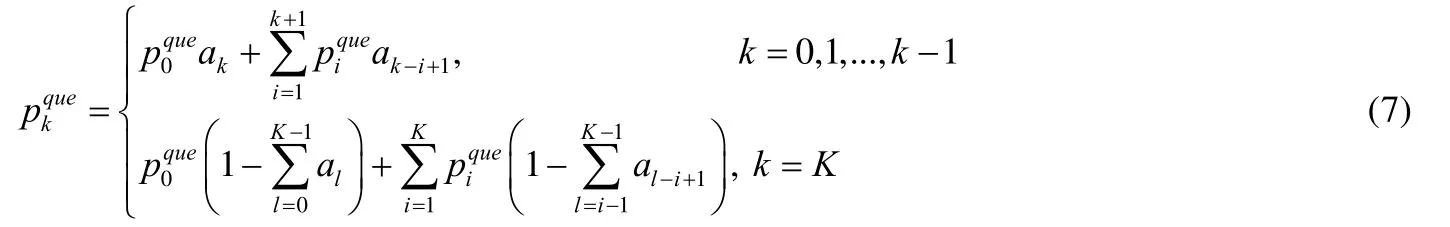
根据M/G/1/K排队模型可以得到缓存队列为空的概率,即车辆在某个时隙没有数据包发送的概率为.其中,是信道被占用的概率,是通信过程的MAC层服务时间分布的均值.

车辆数据包在 MAC层缓冲区排队结束后,进入发送阶段,将 MAC层对数据包的处理过程称为服务系统,系统输入设为概率 1.若数据包侦听到信道忙,则进行指数退避,产生退避延时,该过程结束后,数据包以概率pp再次侦听到信道忙,进入冲突退避过程,也可能由于帧错误需要重新发送,概率为pm–pp,上述过程直到达到重传限制结束传输或者检测到信道空闲成功传输数据,其概率为1–pm.将每个行为都看作是服务系统的子系统,其在时域产生的延时t在z域用zt传递函数来表示.数据包的整个服务系统即为多个子系统的级联,也是多个延时量的叠加,系统的输出即为相应概率取值下的延时因子zt叠加的结果.各项的概率系数为数据包传输过程中不同服务时间对应的概率分布.由上述分析得出,服务系统可看作是线性系统,系统的传递函数即为包服务时间概率分布的生成函数,记为H(z),可以得到其表达如式(8)所示.图2所示为服务系统的框图.

Fig.2 MAC service time linear system diagram图2 MAC层服务时间线性系统框图

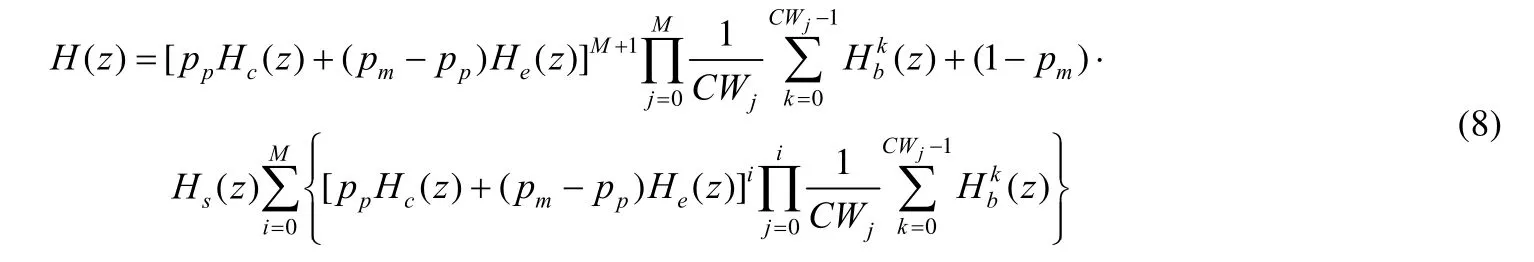
Hc(z)表示数据包发送过程中产生冲突导致传输失败的时间分布传递函数,表示为是数据包传输成功的时间分布传递函数,He(z)是数据包由于信道误码造成传输失败的时间分布传递函数,表示为是竞争信道的退避过程所占用时间分布的传递函数,在本文场景条件下计算为

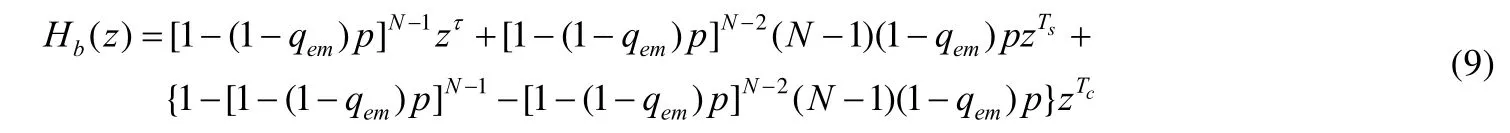
公式中的zτ项系数表示信道处于空闲时隙的概率;zTs项系数表示其他N–1辆车中某一辆成功传输数据包的概率;zTc项系数表示多辆车发送数据包导致信道冲突的概率.退避机制随机地在竞争窗口中选择初值,若检测到信道空闲,则计数器减 1,每次侦听到的信道可能处于空闲状态,也可能发生多个数据包冲突或者出现传输误码的现象,所以退避时间为单个时隙、发生冲突消耗的时间和成功传输数据包的时间三者的概率平均.在概率生成函数中,取[0～CWi]的平均值作为计数器初值,其中,0≤j≤M.

由数据包传输过程中 MAC层的服务时间分布概率表示的概率生成函数为,结合上述传递函数方法的式(8)和式(9),可以得到离散概率psT t.

2.3 Platoon组内车间通信性能度量

基于上述platoon组内车间通信过程的分析,下面给出通信过程的数据包丢失概率和通信延时等网络性能指标.数据包整个传输过程中的延时包括缓冲队列中的排队延时和竞争接入信道的退避延时.本文忽略了数据包在无线信道中的传输时延,也就是车辆成功竞争到资源后发送数据包到达接收方的时间不予考虑.其中,排队的延时由非满队情况下的队列平均长度与包到达速率的比值得到.

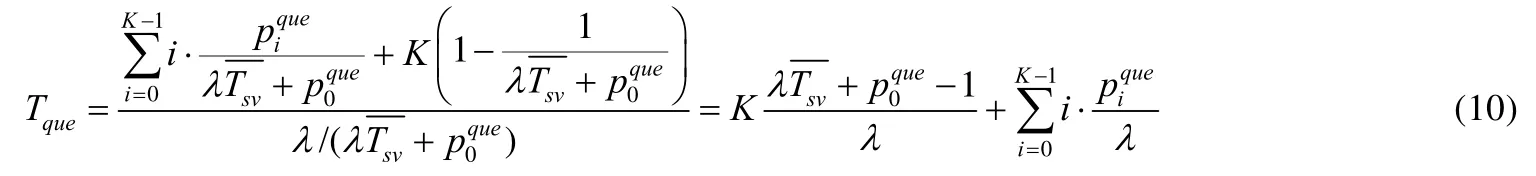
在成功传输情况下,数据包竞争信道的退避过程产生的延时为平均时隙长度乘以退避过程中可能占用的时隙个数,表达如下:

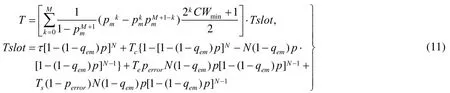
则platoon中车辆之间传递信息的总传输延时为Tdelay=T+Tque;数据包投递过程失败的概率表示为.

为了得到车辆站点间通信的延时和数据包丢失概率等性能度量指标,首先假设通信节点始终有数据包发送,即缓冲区空闲概率qem为0,联立式(2)～式(4)及式(6),计算每辆车发送数据包的概率p以及由于信道误码或者竞争冲突导致数据包发送失败的概率pm;然后利用MAC层服务时间概率分布生成函数H(z),得到离散概率,将其代入式(5),结合迭代方程(7)求得排队系统稳态概率分布pkque,进而得到空闲概率qem,若其大于10–6(设定的容限值),则更新p和pm为缓冲区可能为空情况下的概率,最后联立式(10)、式(11)计算排队延时、退避延时等性能指标,同时可获得包丢失概率及传输延时;若qem≤10–6,则说明当前网络负载条件下,缓冲区空闲的可能性很小,则不更新概率p和概率pm,得到通信网络接近饱和状态的性能度量.

3 Platoons组间通信

本文在分析了 platoon内部通信的基础上,进一步对 platoons组间通信过程进行了研究.假设总共有m个platoons驾驶车队,由于车辆的通信范围有限,前方platoon编组中的车辆想要给后方platoon中的车辆传递信息,需要进行多跳中继.Platoons组间通信模型中作为通信站点的车辆是每个驾驶车队的领导车辆leader和队尾车辆tail,而由于参与通信的车辆角色和位置不同,所以组间通信更为复杂.这里只研究多个platoons组间的单跳通信.所以通信网络中共有2m辆通信车辆,即leader1,tail1,leader2,tail2,…,leader6,tail6,而且参与通信的tail车辆只能与相邻的下一个编组中的leader车辆直接传递消息,同一platoon编组内部的leader车辆和tail车辆可以直接通信,位于 platoons架构中间位置的 platoon leader车辆和 tail车辆可以与前方 platoon的 tail车辆以及跟随platoon的leader车辆通信.下面给出多个platoons组间通信情形下的通信过程及性能分析.

3.1 组间通信的退避过程

在组间通信中,车辆的通信特性不仅与其在 platoon中的成员类型有关,而且与所在 platoon编组相邻的platoons的数量有关.参与platoons组间通信的2m辆车,无论是领导车辆leader还是队尾车辆tail,它们作为通信站点的地位相同,所以形成的通信网络中第i辆车和第2m+1-i辆车的特性相似[23].考虑缓存队列可能为空的情况,在某一给定时隙中,当前车辆发送的数据包与其他相关通信车辆发生冲突的概率如式(12)所示.

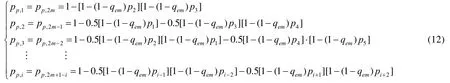
其中,i=1,2,3,…,2m–1,2m,表示通信车辆的位置编号.那么数据包一次传输失败的概率为

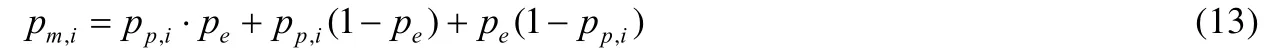
根据 MAC层数据包传输的信道竞争、指数退避过程的 Markov模型以及上述概率性计算,可以得到platoons组间通信架构中不同通信车辆在某个时隙发送数据包的概率pi为

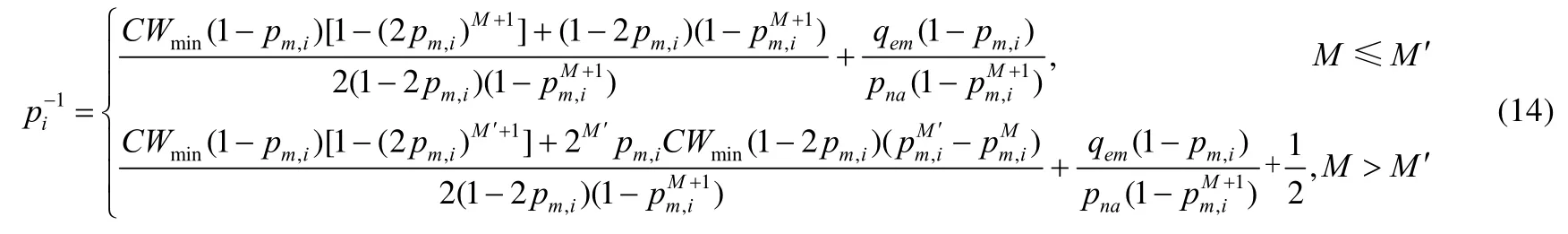
3.2 组间通信MAC层排队过程

Platoons组间通信车辆的数据包在发送之前,仍需在缓冲队列中进行排队.仍然用M/G/1/K排队模型来建模MAC层缓冲区的排队过程,则参与通信的所有platoons领导车辆和队尾车辆的排队系统分析与platoon组内车间通信模型相似,区别在于 platoon组内通信模型中的所有成员车辆在通信网络中是对等的,通信性能相同,排队行为也没有区别.但是,由于 platoons组间通信的关键车辆只可以与相邻的通信站点传递信息,所以通信特性与车辆的空间位置有关,从而针对特定通信车辆的排队行为也有所差异.

位置编号为i(i∈[1,2m])的通信车辆在某数据包服务时间内有k个数据包到达的概率ak,i、不同车辆的包服务时间离散概率分布、排队系统中剩余数据包数量的平稳概率分布以及缓冲区为空的概率q的分em,i析方法同第 2.2节.但是,值得注意的是,公式中的各参量比如发包概率和冲突概率都是针对不同位置的车辆而言的.不同车辆传输数据包时MAC层服务时间分布的概率生成函数如式(15)所示.联立.即可得到不同车辆对应的离散概率分布

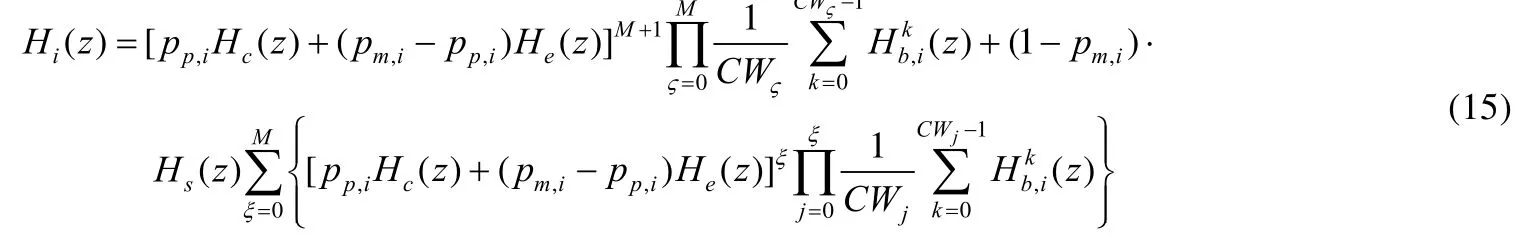
显著差异在于platoons组间通信的退避过程时间概率生成函数与车辆通信范围内的其他车辆有关,且在同一时隙内,当前车辆通信范围之外的数据包投递不会对该车造成影响.若检测到信道非空闲,则可能是争用同一信道资源的其他多辆车发送数据产生了冲突,也可能是仅有一辆车传输数据包到达接收车辆.Platoons组间通信的每个车辆站点检测到信道成功传输通信覆盖范围内某车辆数据包的概率为

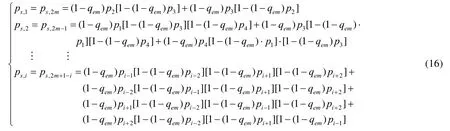
由此重写退避过程的延时概率生成函数为

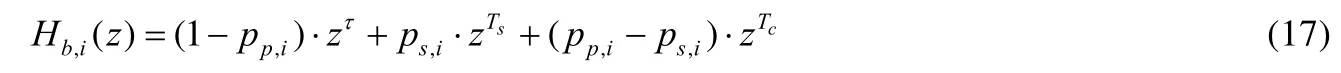
3.3 Platoons组间通信性能度量

Platoons组间通信过程比组内单跳通信更为复杂,涉及到的通信车辆为不同 platoon编组内的成员.参与通信的每辆platoon leader车辆和tail车辆的排队延时有如下计算公式:

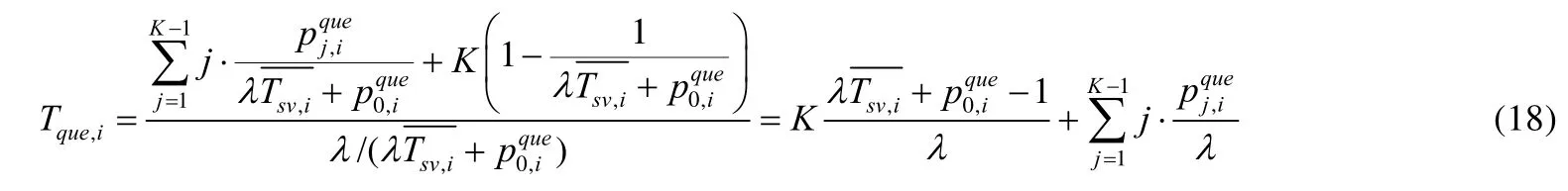
其中,第i辆车的服务时间平均值为.

由于车辆的空间位置不同,所以同时争用相同信道资源的周围车辆不同.从而由于信道忙而进入退避过程产生的延时也应该对不同的车辆分别计算.通信网络中和车辆i争用同一信道资源的其他车辆中仅有一辆车成功投递数据包的概率pc,i和某时隙有车辆发送数据包的概率pt,i的表示如下:

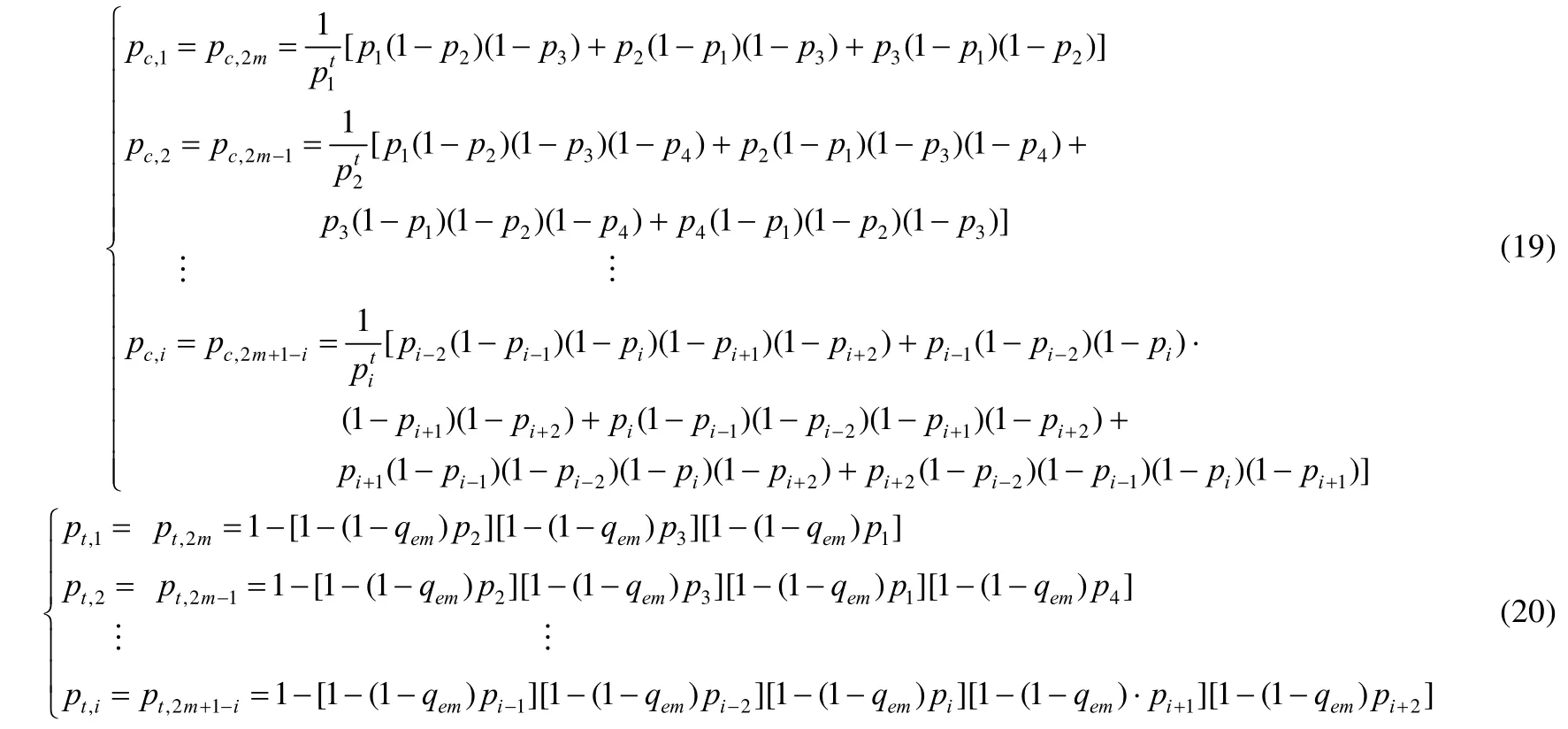
Platoons组间通信的车辆发送数据包时争用信道的退避延时为

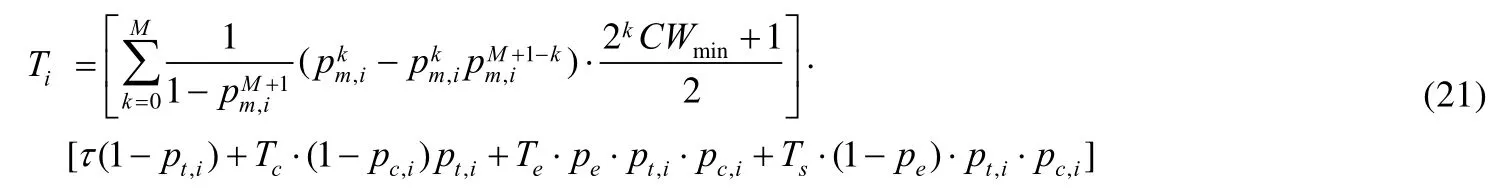
可以得到从首端platoon发出的数据包经过多跳传输到达尾部platoon所经历的延时为

而在首端platoon和尾部platoon之间多跳通信的数据包丢失概率可以计算为

Platoons组间通信过程的网络性能度量计算流程与 platoon组内车间通信过程的流程相似,先假设缓冲区空闲概率qem,i=0,联立式(12)～式(14)求得车辆发送数据包的概率pi和数据包发送失败的概率pm,i;然后结合式(15)～式(17)计算离散概率,再利用排队模型的稳态分布,得到空闲概率qem,i.同样地,若qem,i>10–6,则更新概率pi和概率pm,i,最后结合概率pt,i、pc,i,利用式(18)～式(23)计算不同通信范围的车辆的数据包传输延时、包丢失概率等性能指标;若qem,i≤10–6,则不更新概率pi和概率pm,i,得到近似饱和状态的通信网络各性能指标.

4 实验分析与讨论

对上述提出的platoon组内车间通信过程和platoons组间通信过程的网络性能分析方法进行数值仿真,并采用NS2网络仿真软件进行对比实验.车载环境下通信网络的负载流量表示为Rb=Nλl,其中,N是通信网络中的车辆数目,在 platoon组内车间通信模型中,N代表智能车辆总数,在多个 platoons组间通信模型中,N代表所有platoon的leader车辆和tail车辆总数;λ是单位时间车辆需要传输的数据包个数,称作包到达速率;l为数据包长度,单位是比特.假设车辆节点的通信范围为150m,platoon内部稳定车辆间距为6m,platoon组间间距为40m,车长5m,车辆稳定运动速度为30m/s.本文设定MAC层的最大服务时间Tm为5 000个时隙,系统空闲时隙为20μs,故可表示的最大时间值为 100ms.指数退避过程中的最小竞争窗口尺寸设置为 32,最大退避阶数为 4.其他参数设置见表1.

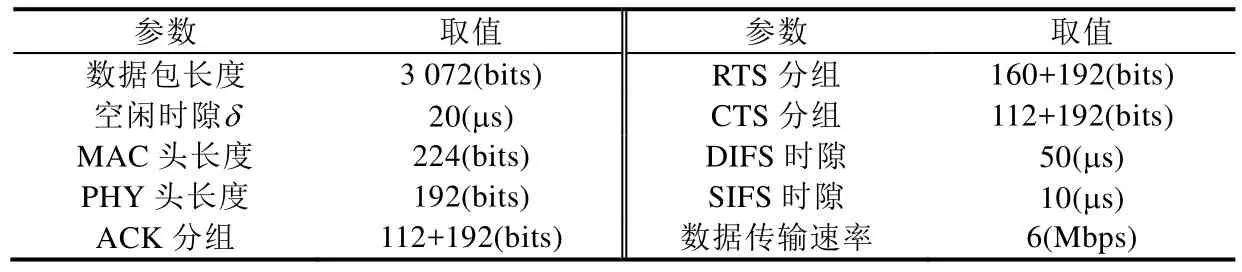
Table 1 Simulation parameter setting表1 仿真参数设置

通过输入platoon编组车辆成员数量、通信网络各关键参数,利用platoon组内车辆间通信过程和platoons组间通信过程的网络性能指标的计算方法可以得到以下数值结果,并将其与仿真软件得到的结果进行对比.

图3(a)和3(b)分别是platoon组内车间通信的排队等待延时、数据包传输总延时和包丢失概率在不同信道条件下随编组内成员数量变化的数值和仿真结果.观察到两者曲线基本一致.同时可以看到,数据包在缓存队列中的排队延时虽然随着成员数量的增多呈上升趋势,但是幅度很小,而包传输总延时随着车辆数量的增加明显上升.这是由于,通信延时主要由排队等待延时和竞争信道的退避延时组成,其中排队延时由 MAC层服务时间概率分布和排队长度决定,而平均排队长度在车辆数量增加幅度不太大时变化并不明显,且车辆站点数量是通过冲突概率的增大间接影响排队延时的,但是接入信道的退避延时和参与竞争资源的通信站点数量直接相关.同时在图 3(a)观察到:信道误码率越高,数据包传输失败的可能性越大,MAC层平均服务时间越长,从而排队延时迅速增加,传输延时也相应增大.图3(b)表明,信道条件对数据包丢失概率的影响非常显著,传输信道误码率越高,包丢失概率随platoon尺寸的变化趋势越陡峭.对一个由8辆车组成的platoon智能车辆队列,当误码率是10–6时,达到最大重传次数数据被丢弃造成的包丢失概率约为0.11%,此时,传输一帧数据出错的概率为7.41×10–6;但当信道误码率高达 3×10–4时,包丢失概率达到了 0.65%.数据包冲突概率是影响包丢失概率的另一个因素,冲突概率被邻居车辆站点传输数据包的总数所影响,故而platoon组内的成员数量越多,导致数据包传输过程中由于和其他车辆发送数据包产生冲突的概率越大,包传输失败的可能性越高.

图4(a)和图4(b)分别呈现了当车辆编组成员是6辆车、8辆车和10辆车的情形下,排队等待延时、包传输总延时和包丢失概率随数据包到达速率λ的变化趋势.在仿真软件中设置发送数据包间隔为均值是 1/λ的指数分布,得到泊松分布的网络负载,进而获取不同包到达速率时的网络性能.设定排队系统的缓冲队列长度为 50,也就是最大可容纳的数据包数量,信道误码率固定为10–4.数据包到达速率即单位时间(1s)内车辆需要传输的数据包个数,在数据包长度一定时,该值和通信车辆的数量共同决定了车载通信网络的数据流量负载.由图 4(a)可知:随着包到达速率的增加,开始排队延时和包传输总延时明显增加,但当λ超过150时,两者都逐渐趋于平缓,最终到达上限,此时通信网络近似达到负载饱和状态,而λ=150之后的数据包传输总延时主要取决于车辆数目,和图3一样的理由,排队等待时延受车辆数目的影响不大.由图4(b)得到:随着包到达速率的增大,数据包到达概率pna增大,需要传输的数据包数量增加,通信车辆间发送的数据包更容易产生冲突,从而包丢失概率增大,而当网络达到饱和时趋于不变,此时冲突概率取决于车辆数目.在λ=150且误码率为 10–5、10–4、3×10–4时,得到的8车platoon组内通信延时数值约为11.30ms、12.75ms、13.44ms.仿真结果约为11.506ms、13.079ms、13.810ms.

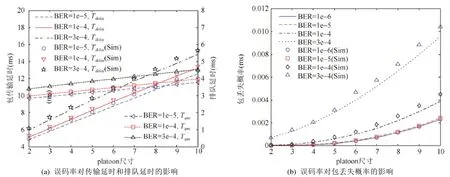
Fig.3 The performance metrics of intra-platoon communication network are affected by BER图3 误码率对platoon组内通信网络性能的影响

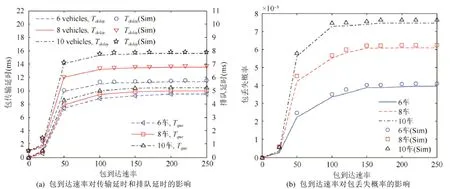
Fig.4 The performance metrics of intra-platoon communication network are affected by packet arrival rates图4 包到达速率对platoon组内通信网络性能的影响

为了对 platoons组间通信性能进行分析,将 platoon数量设置为 6,那么参与通信的车辆为 leader1,tail1,leader2,tail2,…,leader6,tail6.图 5(a)和图 5(b)分别是 platoons组间通信的每个车辆站点在不同信道误码率条件下的包传输总延时以及包丢失概率的数值和仿真结果.考虑到通信半径的限制,只有位置相邻的车辆才可以直接传递数据.图 5(a)表明,随着信道误码率的增大,每辆车的数据包被丢弃的概率都显著增大.相同的传输信道条件下,车辆tail1和leader6的丢包率最低,两端的车辆反而更容易丢包.这是因为,首尾端的车辆只能与其通信范围内相邻的tail1和leader6车辆传递数据,所以发送数据包的冲突概率较高.而tail1和leader6车辆将数据包发送给 leader1和 tail6时,不存在具有相同接收者的其他车辆站点的隐藏终端问题,所以冲突概率较其他车辆要低.同理,由于接入信道的退避时延和发包的失败概率正相关,并且当前车辆的冲突概率还被隐藏终端的发包概率所影响,若隐藏终端在某个时隙内发送数据包的可能性很小,那么当前通信车辆更容易将数据包传输到目的车辆,所以车辆 leader1、tail1以及 leader6、tail6与其他靠近中间位置的车辆相比,包传输总延时较低,tail1和leader6的数据包成功传输的延时最低.

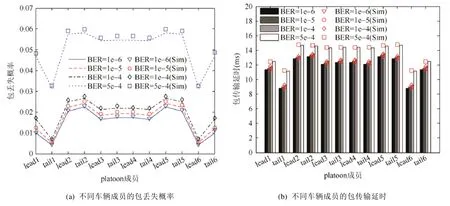
Fig.5 The performance metrics of inter-platoon communication under different channel conditions图5 不同信道条件下platoons组间通信的性能度量

图 6(a)表明,在 platoons组间通信架构中,当数据包到达速率发生变化时传输数据总延时的变化.随着包到达速率的增大,等待发送的数据包增多,平均排队长度变长,缓冲区排队等待时间增加,而且随着网络流量的增加,接入信道的检测和退避行为更加频繁,故而通信延时增加,但当网络流量达到饱和后,延时的上升幅度减小.通过对比不同车辆的包传输延时,可以发现车辆 leader2,tail2,leader5,tail5的延时比中间车辆略长,因为这些车辆更倾向于作为数据传递的中继节点,发送数据包更频繁,而越靠近中心的车辆越可能是数据包的目的车辆.图6(b)对比了最大重传次数和退避阶数不同数值关系下的包传输延时和包丢失概率.若重传次数大于退避阶数,当退避机制到达最大退避阶数时,数据包再次发送失败,通信机制仍会在最大退避状态下重新传输数据,所以,数据包成功传输的概率更高,丢失概率更低,MAC服务时间分布随着冲突概率的减小逐渐向短时间区域集中,缓冲区排队时延下降,但是此时数据包的传输总延时反而会随着重传次数而增加,当M=4时,12辆参与platoons组间通信的车辆中tail2和leader5的数据包传输延时最大,约为13.02ms,排队等待延时约为6.27ms,但当M=6时,tail2车辆和leader5车辆的延时约为14.53ms,相应的排队时延为6.03ms.

设定最大退避次数和最大重传次数都为4,数据包到达速率为150包每秒,信道误码率为10–4,platoon内部成员为 8辆车,其他参数保持不变,得到 6个 platoon组成的车辆编组队列中尾端 platoon车辆接收来自首端platoon通信车辆发送的数据包需要经历的通信延时约为 0.146s.为了验证分析得到的传输数据包时延是否能够满足 platoon的队列稳定性,将最大延时量带入基于前车信息的 platoon线性控制模型中[9].将公式(1)中的kv(t),kv0(t),ka0(t)增益函数都设为0,利用求Hinf控制器的基于线性矩阵不等式的方法对增益函数ke(t)和ka(t)的拉氏变换函数进行求解,并且对期望加速度做拉氏变换,得到如下由加速度误差表示的队列稳定性传递函数:

其中,h是 platoon中车间恒定时间间隔,θ是通信延时,φ是车载制动装置的滞后量.设定h=1s,φ=0.2s,θ=0.146s,可得传递函数的频率响应幅度曲线如图7所示.可以看到,传递函数频率响应的幅度始终小于1,即表示platoon智能车辆编队的加速度误差沿着platoon中车辆传播的幅度是衰减的,保证了行驶队列的稳定性.

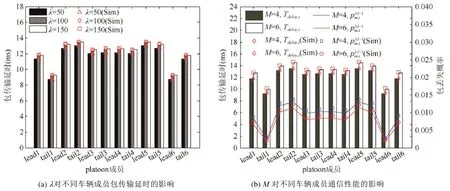
Fig.6 The performance metrics of inter-platoon communication are affected byλ andM图6λ和M对platoons组间通信性能度量的影响

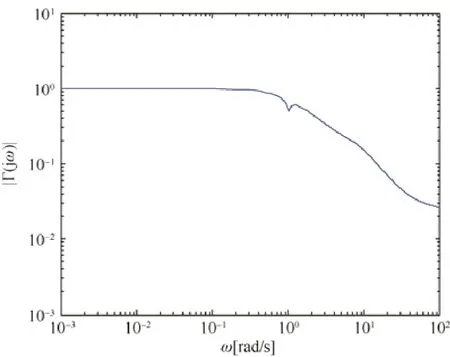
Fig.7 The frequency response amplitude of platoon acceleration error transfer function under 0.146s communication delay图7 通信延时为0.146s时的platoon加速度误差传递函数的频响幅度

5 总 结

本文基于IEEE 802.11p协议对platoon智能车辆编组的DSRC车间通信网络性能进行了分析,通过对DCF争用信道退避机制和MAC层缓冲区排队模型的概率性分析和推导得到platoon组内智能车辆间通信过程和多个platoons组间通信过程的理论分析模型.研究了不同信道比特误码率、网络数据流量负载、退避机制参数以及排队模型对于车间通信的数据包传输延时和数据包传输失败的概率的影响.并且,比较了理论数值结果和仿真实验结果,证明了研究方法对 platoon场景下车间通信网络性能评估的准确性和可行性.最后,通过将分析模型得到的延时带入到一种 platoon控制模型的加速度误差传递函数中,验证了得到的最大延时量可以保证platoon车辆编组的稳定运行.通过分析仿真结果可以得出如下结论:(1) platoon组内或platoons组间车辆站点间通信的数据包传输总延时主要由MAC层缓冲区的排队等待时延和争用信道的退避时延组成,其中排队时延由MAC层服务时间概率分布和平均排队长度决定,受数据包到达速率影响较大,退避时延主要取决于网络数据流量未饱和时的包到达速率和车辆站点数量;(2) 数据包丢失概率在信道误码率一定时,受通信车辆数量和包到达概率的影响较大;(3) 对于platoons组间通信模型,首端和尾端platoon相邻编组中的车辆较其他位置车辆的数据包冲突概率要小得多,故而包丢失概率更小,传输延时也更低,而靠近中间位置的platoon中车辆的数据包传输延时相对较高.

通过上述研究可以得到:platoon中成员车辆数量应该适当地加以选择,既要考虑道路容量,又不能超出leader车辆的通信范围,而且成员过多会导致通信延时和包丢失概率过大,影响信息的有效投递.当 VANETs通信网络中车辆间信息传输较频繁时,可以通过限制同时接入网络的车辆站点数量,减小重传次数和最大退避阶数,以提高通信的时效性.接下来的工作会进一步研究包含中继车辆的 platoons编组多跳通信模型,同时对车间动态通信模型如何影响platoon的控制算法进行探讨.