时移地震“相对差异法”定量预测疏松砂岩油藏含油饱和度——以西非深海泽塔油田为例

陆红梅，徐海，沃玉进，谷宁

（中国石化石油勘探开发研究院，北京 100083）

0 引言

油田开发过程中，当水驱替油或气、油驱替气等流体时置换作用会使岩石孔隙内流体密度增大，地震波传播速度会相应增大；当气驱替油或水、溶解气在地层内脱气等流体置换作用也会使岩石孔隙内流体密度减小，地震波传播速度也会相应减小；油藏开采过程中地层压力的减小会造成岩石孔隙体积缩小，导致岩石密度增大[1]等等，这些油藏开发造成的变化，会使地层的地震波阻抗及地层间的波阻抗差发生改变，从而导致地震反射发生变化，时移地震应运而生。时移地震（又称四维地震）是在油气藏开发阶段对剩余油气分布进行预测的一种技术，通过对同一地区间隔一定时间再次进行地震观测，然后对不同时间观测的地震数据进行互均化处理，以保证资料的一致性，使那些与油藏变化无关的反射信号具有可重复性，并保留与油藏变化有关的反射信号，通过对反射信号差异分析达到对油藏开发动态监测的目的，反射信号差异大说明开发储量动用比较多，反之则说明储量动用少。再综合利用油藏工程资料、岩石物理信息和地质学知识等，对油藏进行综合动态评价，达到优化开发方案，并最终提高采收率的目的。

时移地震预测剩余油所依据的地震资料差异是不同时间地震资料之间的绝对差异，即监测地震与基础地震之差。通过对时移地震绝对差异敏感属性的优选，或开展时移地震弹性波阻抗反演，或结合正演模拟，综合油田开发生产历史等，对油藏剩余油分布进行预测[2-11]，这其中忽略了地层厚度对绝对差异的影响。笔者通过西非泽塔油田应用研究，提出了一种不受储集层厚度影响，仅与流体饱和度变化有关的时移地震新方法。

1 泽塔油田概况

泽塔油田位于西非安哥拉西海岸下刚果—刚果扇盆地南端深海海域，水深1 500 m左右（见图1）。油田储集层为渐新统浊积水道砂体，主要矿物为石英，单砂层厚度为0.8～13.7 m，横向变化大，埋深为海底以下1 500 m以内。构造为向北东方向上倾的断鼻，圈闭类型为受构造和岩性双重控制的复合圈闭。储集层疏松未固结，物性好，主力产层 1#层砂体孔隙度达20%～32%；轻质原油（常温常压下密度为0.865 g/cm3）；注水开采，注采比为1∶1。

该油田于开发之前进行了基础三维地震（数据体B）的采集，油田开发后又陆续采集了3期监测地震（数据体M1、M2、M3）。4期地震由同一家公司采集和处理。地震采集采用等浮拖缆技术和GPS定位控制系统，采用相同的采样时间间隔和相同的采集面元，处理过程中采用严格一致的处理流程与参数，以保证时移地震数据受非油藏因素干扰最小。

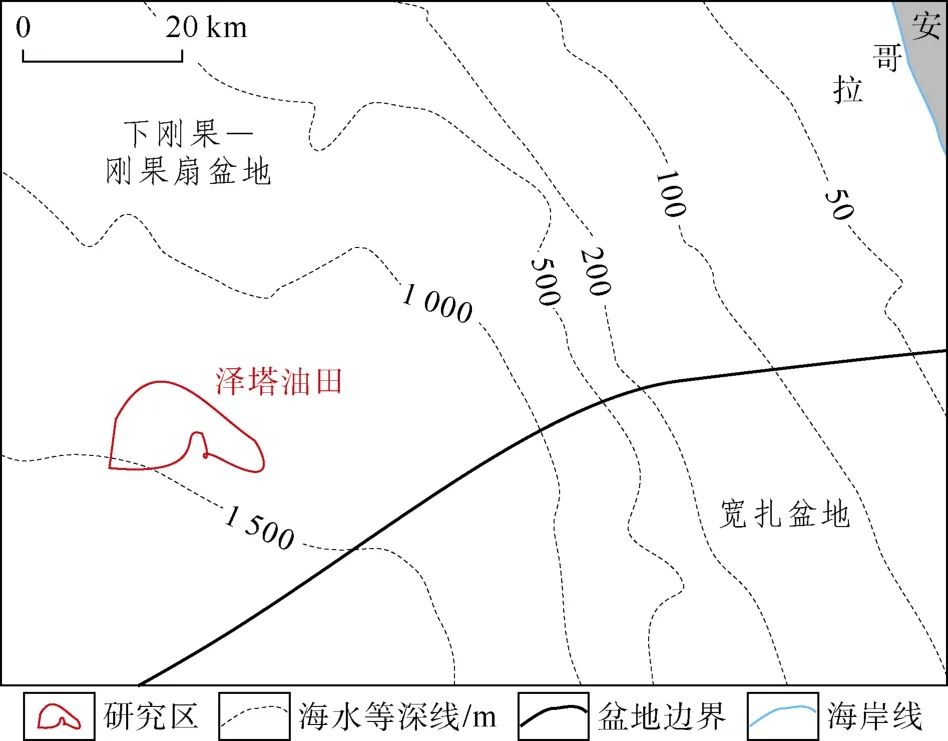
图1 泽塔油田位置图

2 泽塔油田时移地震差异影响因素

基于泽塔油田储集层类型、储集层特征及开发注采比等，基本可以排除油藏开发过程中压力、孔隙类型及孔隙度对时移地震的影响。在温度方面，一般稠油油藏随着开采过程中温度的变化对时移地震会产生相对较明显的变化[12]，泽塔油田原油为轻质原油，温度对地震的影响基本可忽略不计。综上，泽塔油田时移地震可排除压力、温度、孔隙类型及孔隙度的影响。泽塔油田的储集层流体仅限于油和水，但这并不意味着时移地震的差异仅与油和水的饱和度变化有关。由于泽塔油田的浊积砂岩厚度一般都小于地震波调谐厚度（1/4波长），在这种情况下，反射振幅的大小与储集层厚度直接相关。上述 4方面的影响仅针对某一固定的位置点而言，定性分析各点流体驱替是否发生是可行的，但要分析流体驱替发生的程度和定量研究剩余油分布，需有不同位置点的地震反射强度变化量之间的比较，这就必须考虑在地震“薄层”反射中最为敏感的因素——储集层厚度，即必须去除储集层厚度在反射强度变化量中的影响，才能最终保留源于流体饱和度变化的部分。

有关储集层厚度与时移地震差异关系的研究较少，ALVAREZ E等在利用流体界面的延时地震振幅变化来预测剩余油饱和度技术中提出储集层必须满足一定的厚度[9]；鲍祥生等指出地震波平均能量差异的正、负是由储集层地震波速度减小和增大引起的，与储集层厚度不存在正比关系，调谐厚度内的薄层有时比厚层引起的差异要大[10]。以下本文围绕储集层厚度、流体饱和度两方面开展流体置换地震正演模拟研究。

3 Gassmann流体置换地震正演模拟

3.1 Gassmann流体置换基本原理

流体置换即为从一种孔隙流体状态下的岩石物理参数计算出另一种流体状态下的岩石物理参数[13]，它可以反映孔隙流体对地震波速度和波阻抗的影响[14]，为四维地震研究提供了正演模拟及定量分析工具[13]。流体置换通常采用基于wood方程的Gassmann流体置换方法[13]。Gassmann方程是岩石弹性物理研究的重要理论工具，它建立了岩石体积模量、孔隙度、孔隙流体的体积模量、岩石骨架的体积模量、造岩矿物的体积模量之间的关系，是沟通岩石物性参数与地震参数的桥梁[14]。Gassmann方程如下：

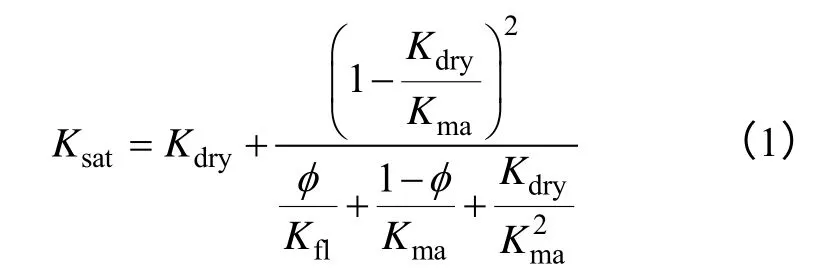
饱和岩石的压缩率可以近似表述为：

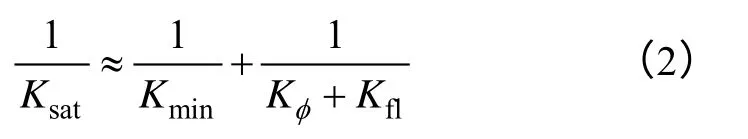
联立（1）（2）式可以得出如下结论：孔隙空间刚度大的硬岩石对孔隙流体的敏感性较小，而刚度小的软岩石对孔隙流体的敏感性较大[12]。

WANG Zhijing[1]、AVSETH P 等[14]、周水生等[13]的研究表明，对于低黏度流体饱和的高孔隙度、高渗透率岩石，聚集于 10～200 Hz的地震数据趋近于Gassmann结果。泽塔油田浊积砂岩储集层符合该条件。

3.2 Gassmann流体置换与泽塔油田岩石物理特征

地震波对流体的敏感性取决于岩石孔隙度和孔隙空间的刚度[14]，图2为反映岩石对孔隙流体变化敏感性的图版[14]，它给出了归一化的岩石体积模量Kdry/Kmin与孔隙度的交会图，图中每一条线代表不同的归一化孔隙空间刚度（Kφ/Kmin），干岩石和水饱和岩石之间的差为图中任意位置的3条等值线的距离。A点和B点对应于同一孔隙度两种不同刚度的干岩石，A′点和B′点分别对应于两种干岩石的水饱和状态。可以看出，从干岩石到水饱和状态，岩石B的归一化体积模量变化比岩石A大，这说明岩石B对孔隙流体的变化更敏感[14]。

将泽塔油田渐新统浊积砂岩样品点投到图2模板中，这些样品点分布在归一化孔隙空间刚度为 0.06～0.10的疏松岩石区域内（见图2），表明泽塔油田渐新统浊积砂岩属于孔隙空间刚度低的“软”岩石，这一点也可从下文中岩石体积模量远小于矿物体积模量得到佐证。以上说明泽塔油田储集层对孔隙流体变化敏感。

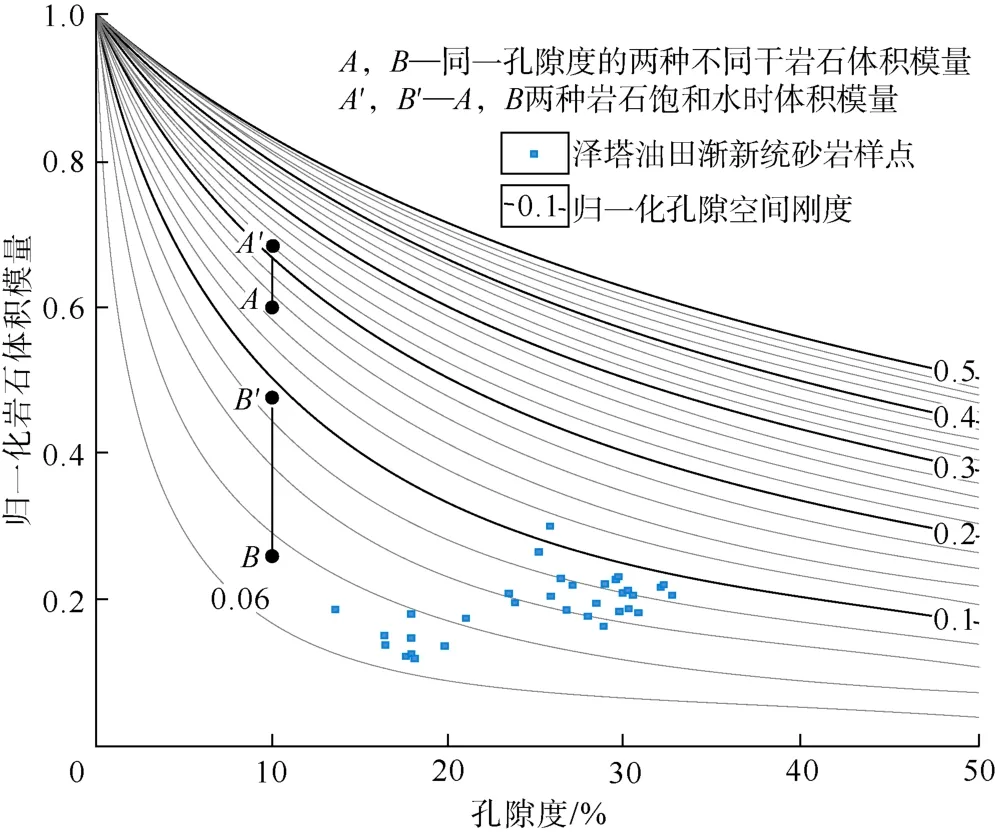
图2 归一化岩石体积模量与孔隙度交会图模板及泽塔油田渐新统砂岩样点分布

将油藏开发前的储集层状态作为初始状态，输入初始参数，对其进行基于wood方程的Gassmann流体置换，随后对该过程进行地震正演模拟，即达到模拟时移地震的效果。由于泽塔油田开发前钻遇的所有油层含水率均在 10%左右，为更加贴近真实情况，流体置换的初始全油模型赋值含油饱和度为 90%、含水饱和度为 10%，对最终理想的全水模型赋值含油饱和度为10%、含水饱和度为90%。

根据测井资料，选择泽塔油田主力产层 1#层中的一个典型油层（见图3），拾取该砂岩油层及其上下泥岩层的数据，将其作为流体置换的初始模型（全油模型），然后输入纵波速度、横波速度、密度、自然伽马值、孔隙度、流体及饱和度、矿物组分及最终状态的流体及饱和度，对其进行流体置换，即将储集层中的原油逐步用水置换，直至全部为水，即可计算出岩石体积模量、密度和纵波速度等参数随流体饱和度变化的数据（见图4）。随之进行地震正演模拟，获得类似于时移地震的地震正演剖面。

在Gassmann流体置换过程中，由于砂岩储集层中油和水的饱和度发生变化，导致孔隙流体的体积模量、砂岩的体积模量、砂岩的密度发生变化，最终导致砂岩的纵波速度及波阻抗发生变化（见图4、表1），而泥岩的速度和密度保持不变，砂岩的上述变化导致砂泥岩接触界面的地震反射相应发生了变化。

图3 泽塔油田典型油层测井曲线

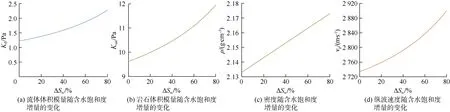
图4 流体置换正演模拟部分弹性参数随含水饱和度增量变化交会图

表1 流体置换初始全含油模型与流体完全置换后各项参数对比表

由于砂岩波阻抗始终小于泥岩波阻抗，即无论流体置换程度如何，在砂岩顶界面处都形成负反射，在底界面处形成正反射，并且“油强水弱”（砂岩含油时地震反射强，砂岩含水时地震反射弱）；在时移地震绝对差异剖面上，同一位置点（储集层厚度前后一致），差异越大反映油水驱替越强。这是泽塔油田能够利用时移地震监测油藏开发效果的岩石物理基础。

3.3 地震正演模拟与储集层厚度影响分析

本次研究设计了不同储集层厚度油水置换模型共5组，图5为本次研究的一个模型，储集层厚度为10 m，子波选用雷克子波，主频为地震资料的主频35 Hz。其中，图5a模型砂岩储集层孔隙流体为全油，图5b模型是一个流体置换渐进模型，储集层流体从右到左由全含油均匀过渡到全含水。可以看到，图5b模型中最右侧一道的地震反射与图5a模型各道完全相同，从右到左地震反射逐渐减弱，表明储集层与上下泥岩的波阻抗差逐渐减小。图5c为图5a模型与图5b模型的地震反射残差（绝对差异，即传统时移地震差异），可以看到最右侧全含油时对应的残差为0，最左侧全含水时残差最大。

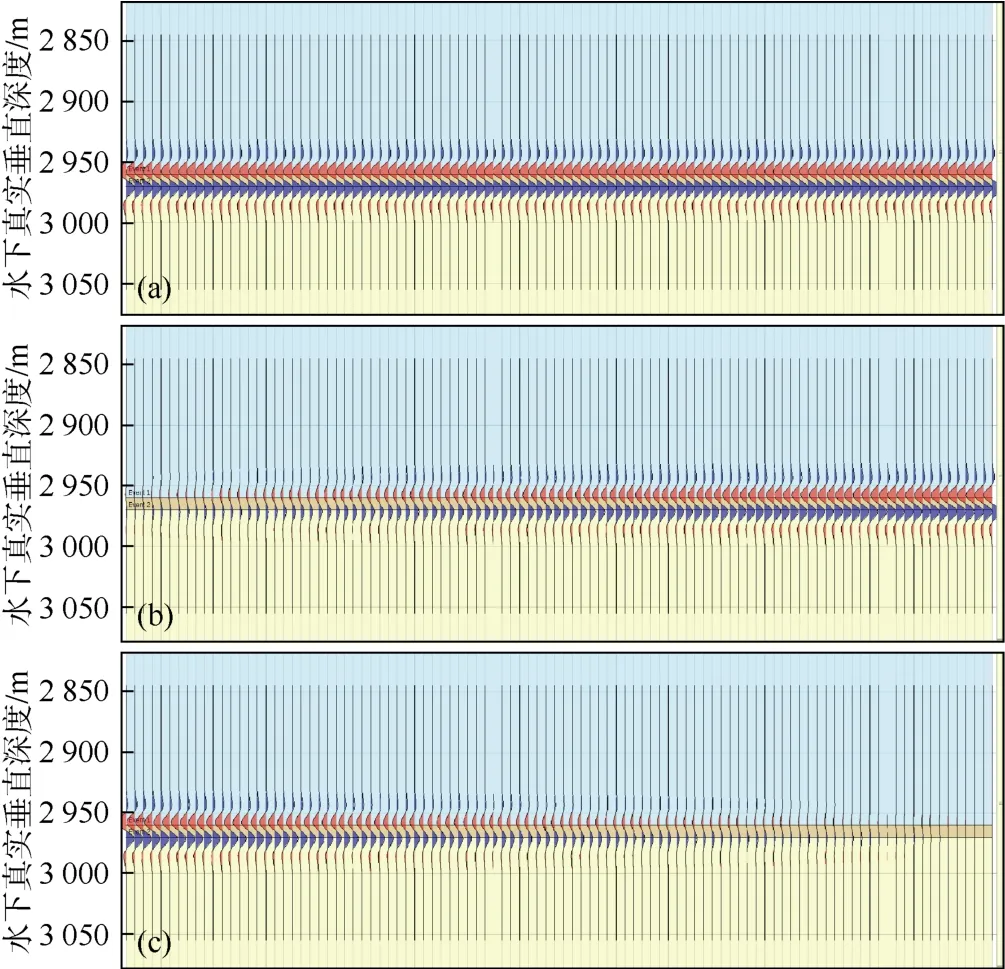
图5 时移地震流体置换地震正演模拟（a、b为泥岩背景中夹一厚度为10 m的薄层砂岩模型的地震正演，a中砂岩储集层流体为全含油，b中储集层流体从右到左由全含油均匀过渡到全含水，c为a与b之差）

该时移地震正演模拟表明：对于厚度为10 m的疏松浊积砂岩储集层，在储集层含油饱和度逐渐减小、含水饱和度逐渐增大的过程中，时移地震的绝对差异逐渐增大；当流体由全含油变为全含水时，其时移地震的绝对差异达到最大。厚度为5 m、20 m、25 m、30 m的疏松砂岩储集层流体置换地震正演模拟可得到以上相同结论。

以覆盖砂岩层顶底的相同长度时窗提取各残差的均方根振幅，并以同一值域范围显示于图6中发现，储集层厚度不同，残差的强弱差异明显。进一步在一张图上分别绘制上述 5个不同储集层厚度模型各道的时移地震绝对差异的均方根振幅与含水饱和度增加量之间的关系曲线（见图7），可以看到，5条曲线随着含水饱和度增加量的增大差异逐渐拉大。当储集层的含水饱和度增加量相同时，不同厚度的储集层，其对应的时移地震绝对差异大小不等，如图7中C到C′点；而对于相同的时移地震绝对差异，储集层厚度不同，含水饱和度增加量也不等，如图7中D到D′点，这说明时移地震绝对差异除了受流体饱和度变化的影响，还与储集层厚度有关。

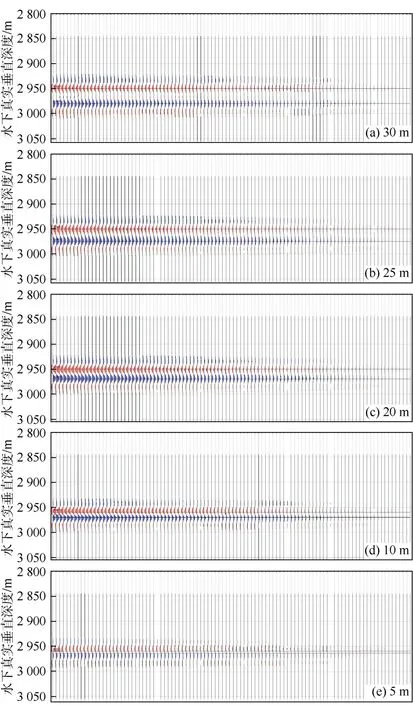
图6 5个不同厚度储集层流体置换模型与全油模型地震反射的残差（按同一值域范围显示，流体置换均为从右到左由全含油均匀过渡到全含水）

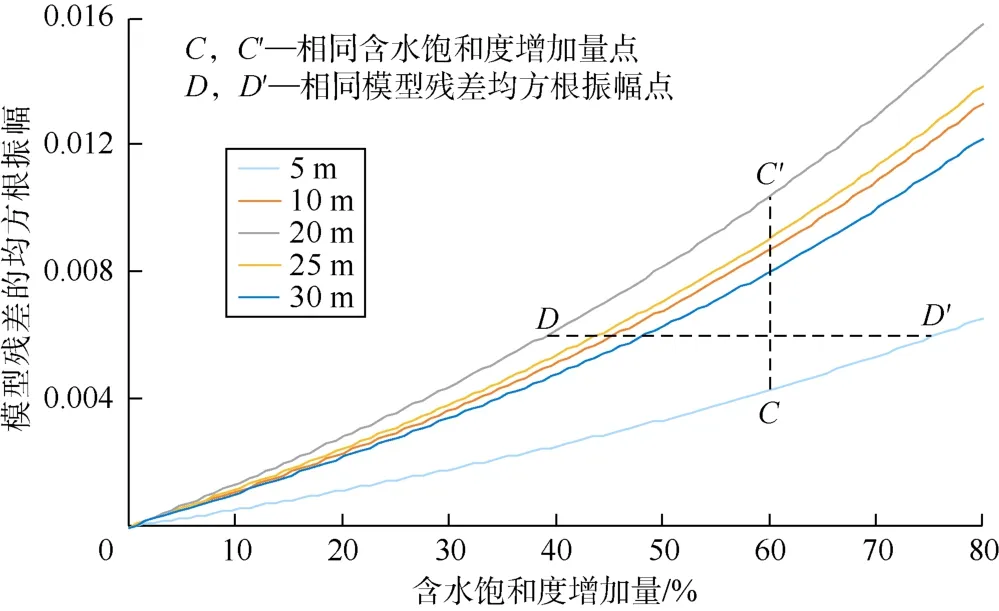
图7 不同厚度砂岩流体置换模型残差的均方根振幅与含水饱和度增加量关系图

众所周知，地震反射是地震子波在地下各个界面形成的反射相互叠加后的综合响应。处于泥岩围岩中的砂岩储集层，其顶底是反射系数大小相等、方向相反的两个界面。当砂岩厚度与调谐厚度相等时，其顶底因两个反射波的相互干涉而使界面处振幅达到最大；接近调谐厚度的砂岩其顶底反射同样因受到干涉而使反射振幅大于单一界面的反射振幅；当砂岩厚度小于调谐厚度时，振幅随砂岩厚度的减小而减小。

根据模型中砂岩的速度（2 733 m/s左右）和地震资料的主频（35 Hz），计算调谐厚度约为20 m。图7中对任意一个相同含水饱和度增加量，厚度为20 m的储集层其模型残差的均方根振幅值总是比其他厚度的大，而厚度最小的5 m砂岩模型残差的均方根振幅值总是最小，厚度为25 m、10 m的储集层仍然受到顶底界面反射的加强干涉，25 m厚的储集层受干涉更大，因此曲线位置比10 m厚模型高，它们的强度都比能够完全分开顶底反射的30 m厚储集层的残差强度更大。按厚度排列，在相同的含水饱和度增加量情况下，模型残差的均方根振幅值由大到小顺序依次为：20，25，10，30，5 m。而在各厚度的初始全含油模型中，厚度为20 m（与调谐厚度相等）的模型其反射振幅最大，均方根振幅值最大；而厚度为5 m的模型其反射振幅最小，均方根振幅值最小；各厚度初始全含油模型的均方根振幅值从大到小依次同样是：20，25，10，30，5 m。即在全含油模型中地震反射强的，发生相同程度的流体置换后，其地震反射残差（时移地震绝对差异）的能量依然强；在全含油模型中地震反射弱的，发生相同程度的流体置换后，其地震反射残差的能量依然弱，而造成这些初始全含油模型地震反射强度不同的，仅仅是厚度一个变化因素。这进一步说明，对一定的含水饱和度增加量，时移地震绝对差异的强弱直接与厚度有关，并同样遵循“调谐效应”及“薄层”反射规律。

因此，时移地震绝对差异的存在仅能说明发生了流体驱替，而流体驱替的程度不能确定。绝对差异越大，不代表流体驱替程度越高。正是因为时移地震绝对差异的大小与储集层厚度密切相关，而泽塔油田储集层厚度一般小于调谐厚度，且横向变化较大，因此，在泽塔油田不能直接用时移地震的绝对差异来计算储集层流体饱和度的变化以及定量预测剩余油分布。

4 时移地震“相对差异法”定量预测剩余油

为定量表征剩余油含量，在传统时移地震改进的基础上，本文提出了时移地震“相对差异”的概念，即监测地震的属性与基础地震的相同属性（本文用均方根振幅）之间的比值。

将上述 5个正演模拟的数据，对各厚度模型的流体置换后的均方根振幅值与全含油模型的均方根振幅值求取比值（即由传统时移地震的求取绝对差异变为求取相对差异），再与流体饱和度增加量交会（见图8），由图8可见不同储集层厚度的交会曲线几乎完全重叠，即时移地震相对差异仅与流体饱和度的变化有关，而与储集层厚度无关。换言之，当储集层内发生相同程度的流体置换时，不同厚度的储集层其地震反射强度的相对变化是相等的；反之，若地震反射强度的相对变化相同，则不论储集层厚度如何，储集层内发生流体置换的程度是相同的。据此可以进行泽塔油田深海疏松砂岩油藏时移地震剩余油定量预测。预测方法的思路如下：首先开展 Gassmann流体置换地震正演模拟，建立时移地震相对差异与含水饱和度增加量之间的关系，求取各期监测地震与基础地震目的层段均方根振幅的相对差异；然后，对相对差异进行转换，获得油藏含水饱和度（或含油饱和度）变化平面分布，从而得到油藏剩余油分布；最后结合储集层厚度分布等数据，计算剩余油储量。

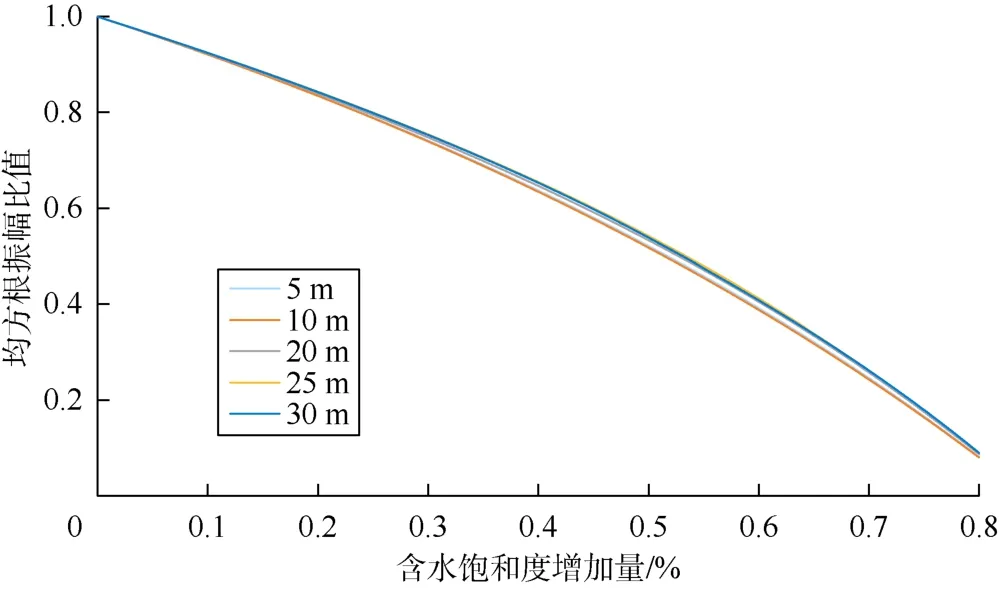
图8 不同厚度砂岩流体置换模型的均方根振幅比值与含水饱和度增加量关系图

时移地震“相对差异法”适用于可排除压力、温度、孔隙类型及孔隙度对地震有影响的深海疏松砂岩油藏，对厚、薄储集层均适用，是一种剩余油定量预测方法，它克服了传统方法不适用于地震“薄层”范畴内的不等厚储集层的局限性，与定性预测剩余油分布的传统方法相比具有明显优越性（见表2）。

表2 剩余油预测时移地震相对差异法与传统方法对比表

5 泽塔油田应用实例

根据泽塔油田的地质、开发实际情况和模型取值，将图8中的含水饱和度增加量转换成含油饱和度，建立地震相对差异与含油饱和度的交会图，拟合关系式如下：

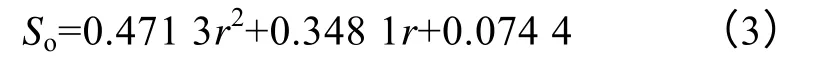
以泽塔油田第3次监测地震（2013年采集）为例，求取监测地震和基础地震（2000年采集）1#层储集层发育段的均方根振幅，求取二者比值，得到相对差异r数据；将r数据代入（3）式，得到油藏含油饱和度So数据；对照油藏1#层砂体分布图（见图9），砂体发育范围内的So数据即为泽塔油田2013年第3期监测地震采集时期1#层剩余油含油饱和度分布（见图10）。

对比油田自投产以来的开发生产数据，以油田西区4口井（P-1井、P-4井、I-1井、I-4井）为例作简要分析。作业者将油田西部砂体发育区作为一个注采井组，共设计实施 4口开发井，采取“多层合采、分层注水”的生产方式。其中，P-1井、P-4井为高部位两口采油井，I-1井、I-4井为两口注水井。I-1井在油藏边界之外，构造位置最低，所钻遇 1#层砂岩全为水层；I-4井位于构造中高部位，所钻遇1#砂岩均为油层。I-1井自 2008年 3月持续对 1#层注水，直至 2017年1月关井；I-4井于2010年3月至2014年2月对2#层注水，直至2016年12封堵2#层并开始对1#层注水（见图11a），即2013年第3期监测地震采集期间，I-4井未曾对1#层注水。

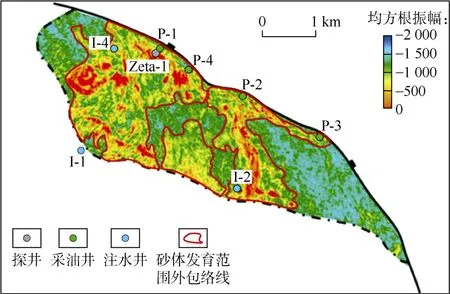
图9 泽塔油田1#层砂体分布图

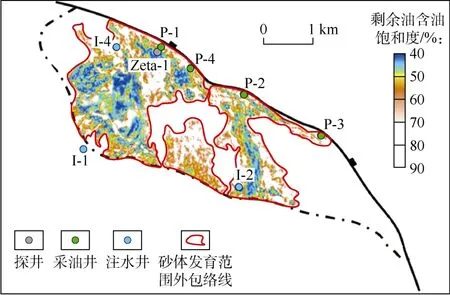
图10 2013年第3期监测地震采集期间泽塔油田1#层剩余油含油饱和度平面分布图

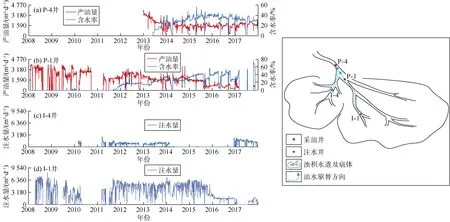
图11 泽塔油田西区4口生产曲线与1#层砂体连通性及注采联动关系示意图

根据I-1、I-4井对1#层注水后P-1井、P-4井的产油量、含水率的变化（见图11a），推断油田西区4口井1#层砂体的注采联动关系如下：I-1井注水对P-1井、P-4井均有贡献，I-4井注水仅对P-4井有贡献。4口井的砂体连通关系如下：4口井1#层砂体全部连通；P-4井在最高部位，P-1井、I-1井是与P-4井连通砂体的一个分支，I-4井是与P-4井连通砂体的另一个分支；两砂体交叉位置高于P-1井（见图11b）。该认识已得到作业者认可，并认定I-4井2017年对P-4井产量的贡献为382 m3/d，大约相当于P-4井产量的10%。这一结论说明，I-4井在未对 1#层注水之前，本井及周边1#层砂体未发生油水驱替。图10显示，2013年I-4井周边1#层含油饱和度在80%以上，与上述分析结果吻合，也与本区开发前1#层油层平均含水率10%左右的实际情况吻合。

6 结论

时移地震的绝对差异不仅与流体饱和度变化有关，也与储集层厚度关系密切。相同的流体饱和度变化条件下，时移地震的绝对差异符合“调谐效应”及地震“薄层”反射规律。对于可排除压力、温度、孔隙类型及孔隙度对地震影响的疏松砂岩油藏，传统的时移地震绝对差异剩余油预测方法仅适用于储集层厚度小于调谐厚度但等厚，或储集层厚度大于调谐厚度的油藏。

时移地震的相对差异不受储集层厚度的影响，仅与流体饱和度变化有关。对于可排除压力、温度、孔隙类型及孔隙度对地震影响的疏松砂岩油藏，根据Gassmann流体置换地震正演模拟建立相对差异与含水饱和度增加量之间的关系，可以直接预测剩余油分布，并进一步结合储集层厚度等数据，定量计算剩余油储量，时移地震相对差异法对厚、薄储集层都适用。该方法在西非安哥拉深海泽塔油田实际应用表明其合理有效。

符号注释：

Kdry——干岩石骨架的体积模量，Pa；Kfl——孔隙流体的体积模量，Pa；Kma——基质（颗粒）的体积模量，Pa；Kmin——岩石矿物体积模量，Pa；Ksat——岩石被体积模量为Kfl的流体所饱和时的体积模量，Pa；φ——岩石孔隙度，%；Kø——岩石孔隙刚度，Pa；So——含油饱和度，%；r——相对差异，即流体置换模型与初始模型或监测地震与基础地震的均方根振幅比值，无量纲；vp——纵波速度，m/s；ρ——密度，g/cm3；ΔSw——含水饱和度变化量，%。