输电线路覆冰过程多元混沌时间序列分析
马宇帆,李奇茂,李 鹏,曹 敏,沈 鑫
(1.云南大学信息学院,云南 昆明 650500;2.云南电网有限责任公司电力科学研究院,云南 昆明 650217)
0 引言
随着社会经济的高速发展,人类对电力系统的依赖越来越强烈。这对电力设施的可靠性、可维护性和安全性提出了越来越高的要求[1]。在自然界中的特殊环境下,输电线路会形成大量的覆冰,从而引发输电网断线、杆塔倒塌等硬件设备损坏的严重事故,对国家生产和人民生活造成巨大的影响。因此,以输电线路的覆冰负荷建模预测作为理论支撑,能够保证电网的安全、稳定运行。
根据自然冰雪灾害对输电线路影响的历史记录,国内外的研究者对此作了很多研究。L.Makkonen[2]从机理角度提出Makkonen模型,将气象因素数值化后建立覆冰预测模型;Masoud Farzaneh和Konstantin Savadjiev[3-4]建立多项式覆冰预测数值模型;Jiang X L和Xiang Z等[5]建立了覆冰厚度的等效预测模型;刘胜春[6]的仿真试验结果表明,覆冰强度与气象因素和线路结构相关。上述学者皆未考虑到时间因子对覆冰增长的影响,而其他学者则往往从时间因子角度对覆冰过程进行分析和预测。王敩青和戴栋等[7]得出覆冰负荷与时间序列符合一次函数关系;Li Peng等[8]建立基于反向传播(back prepagation,BP)神经网络的覆冰过程时间序列预测;刘宏伟[9]等建立了输电线路覆冰厚度短期多变量预测模型;Li Peng等[10]建立了多变量时间序列覆冰预测模型。
鉴于以往学者对输电线路覆冰过程分析时未考虑混沌时间序列的问题,本文运用主成分分析(principal component analysis,PCA)方法对微气象因子降维,并计算其最佳延迟时间和最小嵌入维数;通过最大Lyapunov指数,判定微气象因子时间序列都具有混沌特性;重构了多元混沌时间序列的相空间。
1 多元混沌时间序列基本原理
1.1 混沌时间序列
自1990年以来,混沌一词就已经在相关的科学文献中被记载。混沌学科没有单独作为一门学科,而是与物理学科和数学学科相互结合。从本质而言,混沌就是研究自然界和物质的发生过程。其目标是研究对象的演化过程,而不关心其最终的状态,因此也被定义为关于演化的学科。从时间序列角度出发,对混沌行为进行研究。基于相空间理论,决定系统变量的时间演化记录了整个系统的长期演化的信息,因此可以借助研究混沌时间序列来研究覆冰过程混沌行为。其中:吸引子不变量-Lyapunov指数在混沌方面起着重要作用。如今,混沌时间序列被广泛应用于网络节点流量分析、安全通信、医学工程、经济等领域[11]。
1.2 多变量时间序列的相空间重构
随着混沌学科的发展,本文从混沌时间序列对覆冰过程进行分析。在输电线路的覆冰过程中,首先将时刻变化的覆冰负荷数值化,并转化为覆冰过程的时间序列。构建覆冰过程相空间是研究覆冰过程混沌时间序列的首要条件。Takens原理提出,可以将单变量时间序列重构成与原系统等价的相空间,并根据该空间对时间序列进行混沌分析。构建相空间时,学者普遍使用坐标延迟重构法,具体原理如下[12]。
针对覆冰负荷时间序列{xi,i=1,2,3,...,n}(n为时间序列长度),重构后相空间原系统拓扑结构为:
X(m,τ)=(xi,xi+τ,…,xi+(m-1)τ)i=1,2,…,M
(1)
式中:m为相空间的嵌入维数;τ为相空间的时间延迟;xi为相空间中的点;m为相空间相点的总数M=n-(m-1)τ。
本文中,覆冰过程与多个微气象因素具有密切的关系,即存在多个时间序列。本文重构了包含多个微气象因子时间序列的相空间,其形式如下[13]。
X=[X1,X2,…,XN]
(2)
式中:X由N个单变量时间序列的重构相空间组成。
2 输电线路覆冰过程多元混沌时间序列模型
输电线路覆冰过程包括发生、增长、轻微、严重、脱落及消融等多个过程。对于气候变化较为复杂的滇东北或滇西北低纬度高海拔地区,同一线路通常在1~2个月内经历多次覆冰—融冰的过程,具有强烈的非线性,且覆冰的形成有不同的影响因子。因此,在建立模型之前,必须考虑非线性的覆冰过程,并选择合适的覆冰影响因子。
2.1 输电线路覆冰过程主元分析
主元分析法的算法流程如图1所示。

图1 算法流程图
首先,对覆冰形成条件进行分析,并对其影响因子进行选择。本文将现场采集的微气象因子(温度、湿度、风速、风向、日照强度和气压)作为参考的影响因子。但是若将所有微气象因子作为模型的输入量,则存在冗余的变量和噪声干扰,降低了模型的泛化性能。因此,合理确定主元很重要。
主元分析是一种特征提取方法,通过全面分析众多指标中所带有的信息,选出一些潜在的重要指标,既减少了指标的个数,又最大限度地反映出以往所有指标的信息。本文将其应用于提取重要的影响覆冰过程的微气象因子。
采用主元分析法,对历史覆冰及微气象数据进行分析。微气象因子的降维结果如表1所示。

表1 微气象因子的降维结果
由表1可知,环境温度、空气湿度、风向、日照强度这4项微气象因子的累积贡献率为0.87(即87%),已经超过85%。因此,将这4项微气象因子确定为主元,而不考虑风速、大气压力这2项微气象因子。
2.2 输电线路覆冰过程相空间重构
由于覆冰过程具有非线性及多变量特性,因此可将其看作一个混沌的时间序列过程,进而以重构相空间的方法来解决覆冰微气象多变量参数与非线性覆冰负荷变化。
基于2.1节降维结果,将环境温度、湿度、风向和日照强度作为影响覆冰的主元,并根据Takens嵌入原理,可以得到覆冰和微气象数据构成的多变量时间序列的重构相空间。
X(n)={q(n),q(n-τi),…,q[n-(mi-1)τ1],T(n),T(n-τ2),…,T[n-(m2-1)τ2],H(n),H(n-τ3),…,H[n-(m3-1)τ3],W(n),W(n-τ4),…,W[n-(m4-1)τ4],S(n),S(n-τ5),…,S[n-(m5-1)τ5]}
(3)
式中:n为样本数量;τi为最佳延迟时间;mi为最小嵌入维数;q、T、H、W、S分别为覆冰负荷、温度、湿度、风向、日照强度。
欲确定相空间结构,则需确定τi和mi。
2.2.1 最佳延迟时间确定-自相关法
在构建相空间结构时,延迟时间τ的选择是关键。求取延迟时间的方法很多。本文利用自相关法求最佳延迟时间。
构建微气象因子的时间序列{xi,i=1,2,…,n},可知延迟时间为τ。自相关法原理是在确定j后,逐渐增大τ的取值,并计算每一组对应值的自相关函数L(jτ)。如式(4)所示,观察L(jτ)的图像,当其与初始值的(1-e-1)的这条直线相交,其所对应的τ即为时间延迟[14]。
(4)
计算覆冰负荷、温度、湿度、风向和日照强度气象因子时间序列的时间延迟。微气象因子时间延迟曲线如图2所示。

图2 微气象因子时间延迟曲线
由图2可以看出,风向的时间延迟最低,日照强度的时间延迟最高。
采用自相关法求最佳延迟时间,则图2自相关函数曲线与直线的交点的延迟时间为重构相空间的最佳延迟时间。采用自相关法,仿真所得各时间序列相空间重构的微气象因子最佳延迟时间如下。温度为27 min,湿度为31 min,风向为2 min,日照强度为38 min,覆冰负荷为22 min。
2.2.2 最小嵌入维数确定-伪最近邻法
嵌入维数的选择方法也很多,如饱和嵌入维数法、伪最近邻点法等。本文选择伪最近邻方法来求取最小嵌入维数,具体步骤如下。
①输入时间序列{x(1),x(2),…,x(N)},基于延迟时间τ,假设初始的嵌入维数为m,构建相空间Xm(i)。
③结合2个判据,选择嵌入维数m。
伪紧邻点判据一:
式中:Rtol可以在[10,50]中进行选择。
判据二:

逐渐增大m,当假近邻率不再随着m的增加而减少时,最小嵌入维数即为此时的m[15]。计算温度、湿度、风向和日照强度气象因子的时间序列的嵌入维数。微气象因子嵌入维数曲线如图3所示。
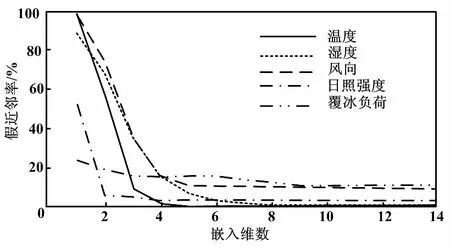
图3 微气象因子嵌入维数曲线
由图3可知,采用假近邻法,微气象因子嵌入维数如下。温度为4,湿度为8,风向为5,日照强度为4,覆冰负荷为9。
3 输电线路覆冰过程混沌特性验证及模型确定
目前,电网公司已经广泛使用输电线路覆冰在线监测系统。该系统可监测到架空输电线路实时覆冰重量,以及输电线路附近的环境温度、空气湿度、风速、风偏角、日照强度、大气压力等微气象数据。
本文仿真数据由南方电网公司提供。该数据是2009年11月到2010年1月期间云南东北部“桃洛熊”高压架空输电线覆冰在线监测系统获得的输电线覆冰和相应的微气象数据信息。该信息采样间隔为20 min。全部仿真结果基于Matlab2015a平台。
3.1 数据预处理方式
3.1.1 日照均值化处理
日照数据均值化,即将昼夜一日的日照强度进行平均并显示。原始数据的均值化处理如式(5)所示。
(5)

3.1.2 数据标准化处理
本文中不同微气象数据的量纲是不一样的,因此必须进行无量纲化处理。采用了min-max标准化方法,将其定义在[0,1]之间。转换函数如下:
(6)
式中:yi为预处理的数据;ymax和ymin分别为预处理数据中的最大值和最小值。
3.2 Lyapunov指数的定义
对初始值非常敏感是混沌系统的基本特征。Lyapunov指数用于定量描述由两个类似的初值所产生的轨迹,它们随时间指数分离。在实际应用中,无需计算Lyapunov谱,只要计算最大的Lyapunov指数λ。若λ>0,即判定系统存在混沌行为[16]。
分别计算温度、湿度、风向、日照强度和覆冰负荷的最大Lyapunov指数λ如下。温度为0.062,湿度为0.029 5,风向为0.161,日照强度为0.131 1,覆冰负荷为0.309 2。
根据λ值进行判断:λ>0则为混沌时间序列。因为温度、湿度、风向、日照强度和覆冰强度微气象因子时间序列的最大Lyapunov指数都大于0,所以皆具有混沌特性。故可构建输电线路覆冰过程多元混沌时间序列模型。其多微气象因子时间序列的重构相空间为:
X(n)=[q(n),q(n-22),…,q(n-176),T(n),T(n-27),…,T(n-81),H(n),H(n-31),…,H(n-217),W(n),W(n-2),…,W(n-8),S(n),S(n-38),…,s(n-114)]
(7)
式中:n为样本数量;q、T、H、W、S分别为覆冰负荷、温度、湿度、风向、日照强度。
4 结束语
本文采用云南东北部“桃洛熊”高压架空输电线的实际覆冰数据进行仿真试验,基于PCA降维结果,剔除不必考虑的微气象因子。从时间序列的角度出发,首先使用自相关法求取最佳延迟时间;再利用伪最近邻法求取最小嵌入维数,并通过最大Lyapunov指数判定所有微气象因子时间序列皆具有混沌特性;最后重构了多元混沌时间序列的相空间。根据相关的混沌理论,该分析能为覆冰负荷预测提供新的研究途径。

