永磁同步电机电流调节器性能研究
杜玉亮
(1 中国铁道科学研究院集团有限公司 机车车辆研究所, 北京 100081;2 北京纵横机电科技有限公司, 北京 100094)
随着轨道交通行业的发展,高速动车组列车电传动系统轻量化、高效能已成为路内技术研究的重要方向[1]。与目前我国动车组列车普遍采用的异步电机不同,永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)转子为永磁体结构,它无需转子励磁电流,因而功率密度和电机效率更高[2]。永磁牵引技术在轨道交通领域彰显出强大的活力,阿尔斯通、西门子、东芝、中车株洲所等国内外轨道交通装备供应商均已完成永磁同步电机在轨道交通装备上的开发应用和装车运行。
电流调节器作为永磁同步电机矢量控制的内环,其动态性能和鲁棒性直接影响永磁同步电机控制性能[2-3,5]。矢量控制中,通过坐标变换将电机定子三相电流转换为同步旋转坐标系(Synchronous Rotating Frame, SRF)dq轴下直流量进行控制,但静止坐标系到同步旋转坐标系转换后,电机定子dq轴之间存在交叉耦合,随着电机转速的升高会影响电流内环的动态性能[3,6-7]。
文中推导了永磁同步电机复矢量数学模型,基于该模型对同步旋转坐标系前馈/反馈解耦PI电流调节器和同步旋转坐标系复矢量电流调节器的控制器性能做了对比分析。理论分析和仿真结果验证了同步旋转坐标系复矢量电流调节器优异的动态性能。
1 永磁同步电机复矢量数学模型[4]
定义复矢量变量
(1)
永磁同步电机在静止坐标系下的复矢量数学模型如式(2),式中上标“s”表示静止坐标系
(2)
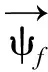
(3)
复矢量变量由静止坐标系转换为同步旋转坐标系时有
(4)
上标“r”表示同步旋转坐标系。由式(4)可知,微分运算转为同步选坐标系如式(5)
(5)
其中p代表微分算子,将式(4)式(5)代入式(3)可得同步旋转坐标系下定子电压矢量方程
(6)
化简后可得同步旋转坐标系永磁同步电机定子电压复矢量方程
(7)
式中
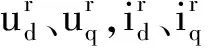
由式(7)可以得到永磁同步电机d轴和q轴电压方程矩阵为
(8)
2 永磁同步电机电流调节器动态性能分析[3]
采用复矢量描述永磁同步电机模型可以简化分析,永磁同步电机数学模型由多输入多输出系统变换为单输入单输出系统。由式(7)可以得到永磁同步电机复矢量模型为
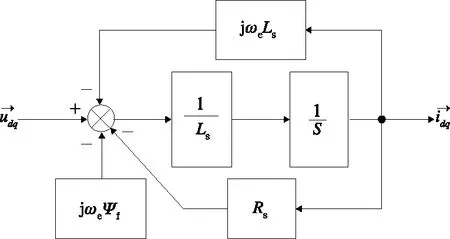
图1 永磁同步电机复矢量数学模型
图1 中永磁磁链产生的反电动势项jωeψf可以作为一个常量,假设不考虑其影响,则永磁同步电机复矢量数学模型在同步旋转坐标系下传递函数如式(9)
(9)
式(9)可以看出PMSM模型中包含一项与同步角频率相关的耦合项jωeLs。随着电机转速的升高,dq轴交叉耦合项jωeLs随同步频率增大而增大。因此dq轴交叉耦合项的解耦处理是永磁同步电机控制的关键,直接影响中高速段电机控制性能。
2.1 基于状态反馈解耦的同步旋转坐标系PI电流调节器
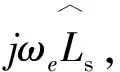
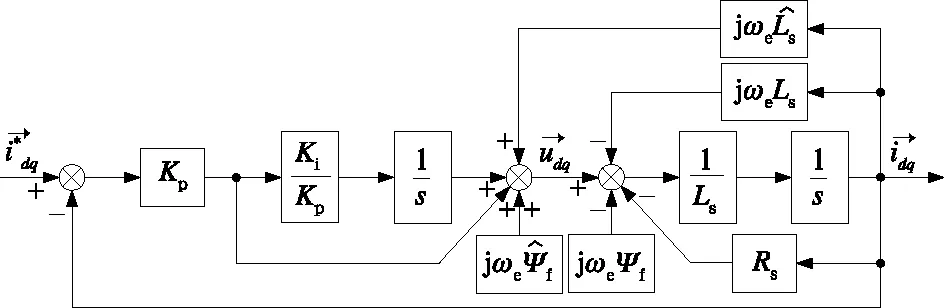
图2 状态反馈解耦的同步旋转坐标系PI电流调节器控制框图
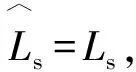
由图2可推导状态反馈解耦系统闭合传递函数如式(10)
(10)
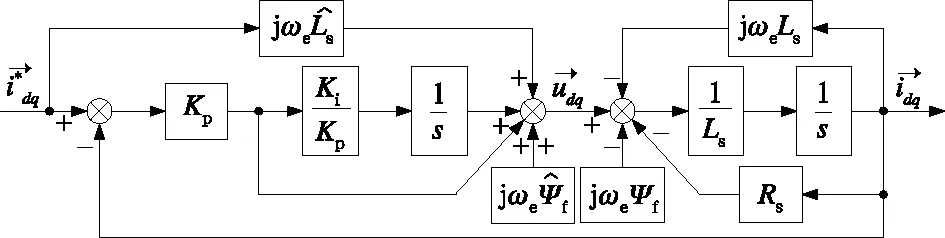
图3 基于前馈解耦的同步旋转坐标系PI电流调节器控制框图
根据图3可知,基于前馈解耦的同步旋转坐标系PI电流调节器闭环传递函数为
(11)
图4是永磁同步电机同步频率从0到100 Hz变化时,基于前馈解耦的PI电流调节器系统闭环零极点变化情况。
基于前馈解耦同步旋转PI电流调节器零点Z1轨迹如图4中所示,零点Z1轨迹试图抵消变化的主导极点P1。由此可知,基于前馈解耦同步旋转PI电流调节器的本质是通过改变系统零点位置以抵消耦合项的影响,但其传递函数中仍存在耦合项,耦合未完全抵消,随着同步频率的升高,主导极点P1向虚轴移动表明系统仍有不稳定趋势。
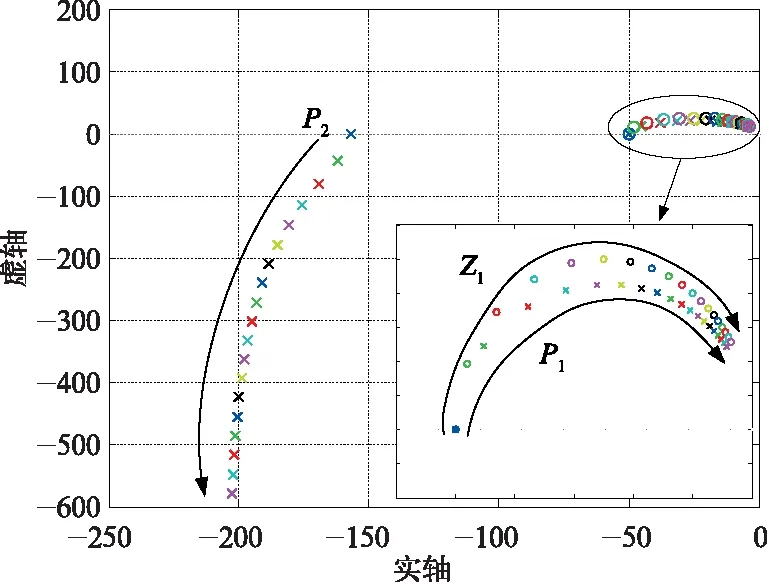
图4 基于前馈解耦的同步旋转坐标系PI电流调节器零极点分布图
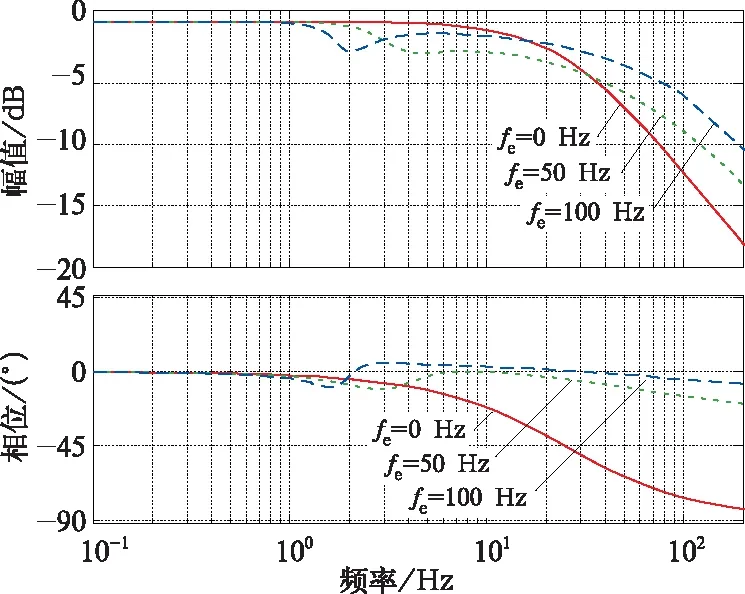
图5 基于前馈解耦同步旋转坐标系PI电流调节器波特图
图5给出了前馈解耦方法的波特图,当系统同步频率fe增大时,如图中fe=50 Hz、fe=100 Hz,系统幅频特性和相频特性均与零速时幅频特性和相频特性有所差异。
2.2 同步旋转坐标系复矢量电流调节器
改善电流调节器性能、消除耦合项影响的另一种方法是:不改变被控对象极点位置,对电流调节器进行改进,使电流调节器产生与被控对象极点位置相同的复零点,以满足零极点对消条件达到消除耦合的目的。
同步旋转坐标系复矢量电流调节器控制结构如图6所示。
根据图6可知,基于复矢量电流调节器系统闭环传递函数为式(12)
(12)
复矢量电流调节器的核心是改变PI电流调节器的结构,将PI调节器的零点由-Ki/Kp移至-Ki/Kp-jωe,这样系统零点与主导极点能时刻相抵消。此外,复矢量电流调节器只需要控制器满足Ki/Kp=Rs/Ls即可实现解耦控制,与电机电感Ls无关,因此复矢量电流调节器对电机参数的依赖程度远低于前馈解耦方法。
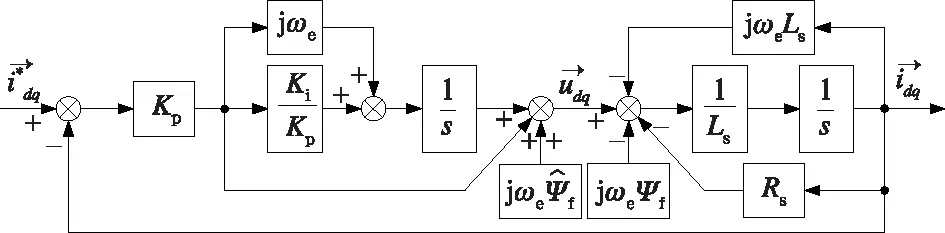
图6 基于同步旋转坐标系复矢量电流调节器控制框图
图7是永磁同步电机同步频率从0到100 Hz变化时,同步旋转坐标系复矢量电流调节器系统闭环零极点变化情况。由于在电机任何同步频率处,复矢量电流调节器均能实现其主导极点与零点相抵消,如图中P1、Z1所示,因此系统整定为典型I型系统。同样地,同步旋转坐标系复矢量电流调节器波特图也可以在任意同步频率处均具有理想的带宽,这里不再给出。
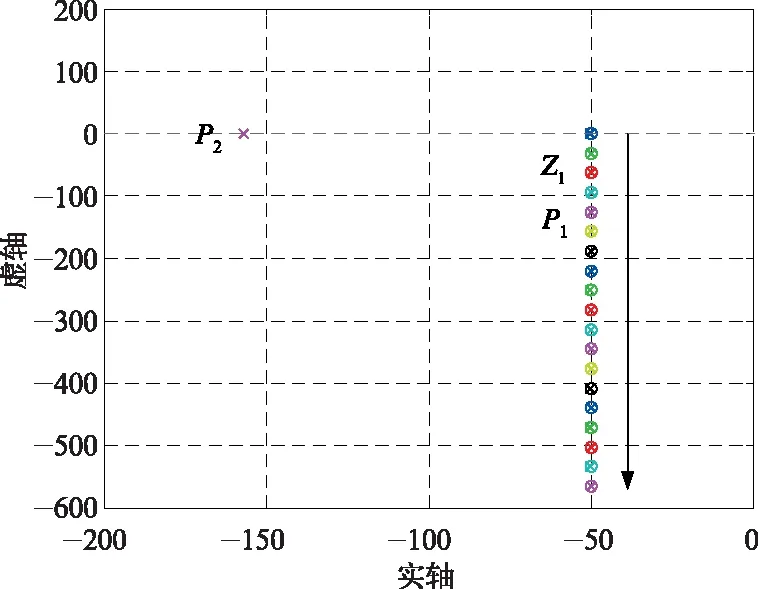
图7 基于复矢量电流调节器零极点分布图
2.3 两种电流调节器对比
基于反馈解耦电流调节器和复矢量电流调节器是两种行之有效的控制方法,两者本质上是一致的,都是试图改造系统主导极点或控制器零点位置,以实现主导极点和零点相互抵消。下面从两方面对这两种电流调节器进行比较。
(1)对电机参数依赖性
基于反馈解耦电流调节器系统闭环传递函数如式(13)
(13)
可以看出当电机参数估算准确时,系统是典型I型系统。
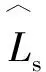
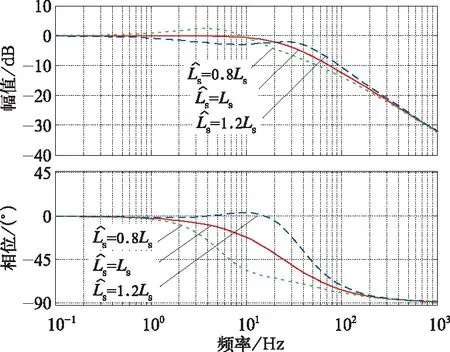
图8 电机参数估算差异下反馈解耦电流调节器波特图(fe=100 Hz)
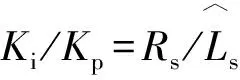
当电机参数估算准确时,复矢量电流调节器可以取得良好的带宽性能。当参数估算不准确时,如图8中绿线和蓝线所示,复矢量电流调节器性能受到一定影响,但与红线相比差异非常小。此外,复矢量电流调节器相比反馈解耦PI电流调节器具有更好的电机参数鲁棒性,其对电机参数依赖性更小,展示出更强的抗干扰性能。
(2)交叉耦合程度
电机电流调节器除了要具备更弱的电机参数依赖性,还应对电机交叉耦合项实现良好的解耦效果。上面分析可知,电机交叉耦合程度与同步频率密切相关,一般来说随着同步频率的升高较差耦合程度愈强。
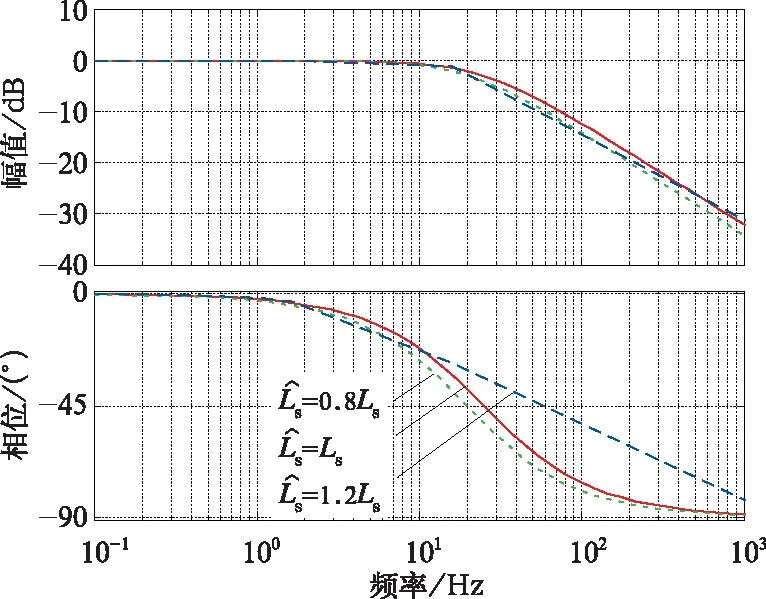
图9 电机参数估算差异下复矢量电流调节器波特图(fe=100 Hz)
系统闭环传递函数均可写为式(14)形式
(14)
理想情况下,|Gclo(s)|=1,表明系统电流实际值与指令值可实现零静差跟踪。实际中,系统交叉耦合是由坐标变换复数因子j引来的,因此在系统闭环传递函数中,虚部Im{Gclo(s)}反映了系统交叉耦合的程度。由此可以定义式(15)表达式,观测其幅频特性曲线,幅值越大则表明交叉耦合频率响应的耦合越大。
(15)
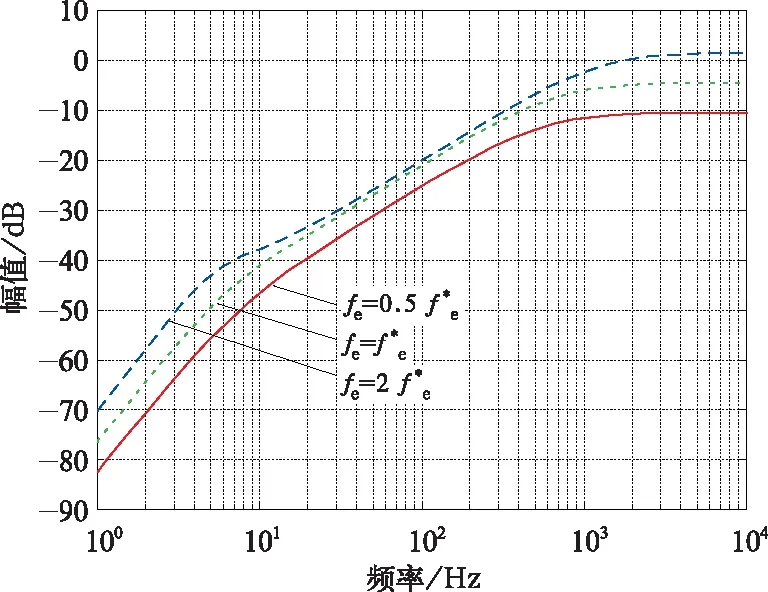
图10 前馈解耦PI电流调节器交叉耦合响应(f*e=300 Hz)
图10给出了前馈解耦PI电流调节器交叉耦合响应图,可以看出随着电机同步频率fe增加,交叉耦合响应的幅值也随之增加,这说明交叉耦合响应加重。由此可得,对于前馈解耦PI电流调节器,同步频率越大耦合含量越高。
相反地,复矢量电流调节器能够实现系统主导极点和零点完全抵消,不随同步频率的改变而受到影响。因此复矢量电流调节器能够实现在任意频率处的完全解耦控制。
3 仿真验证
分别选择低速2 000 r/min和高速12 000 r/min两种情况进行仿真。在每种情况下,分别改变d轴和q轴电流指令值,观察另一电流变化情况。d轴电流指令值在0.3 s由-10 A阶跃至-30 A,q轴电流指令值在0.2 s 由10 A阶跃至30 A。系统带宽频率设计为2 000 Hz。
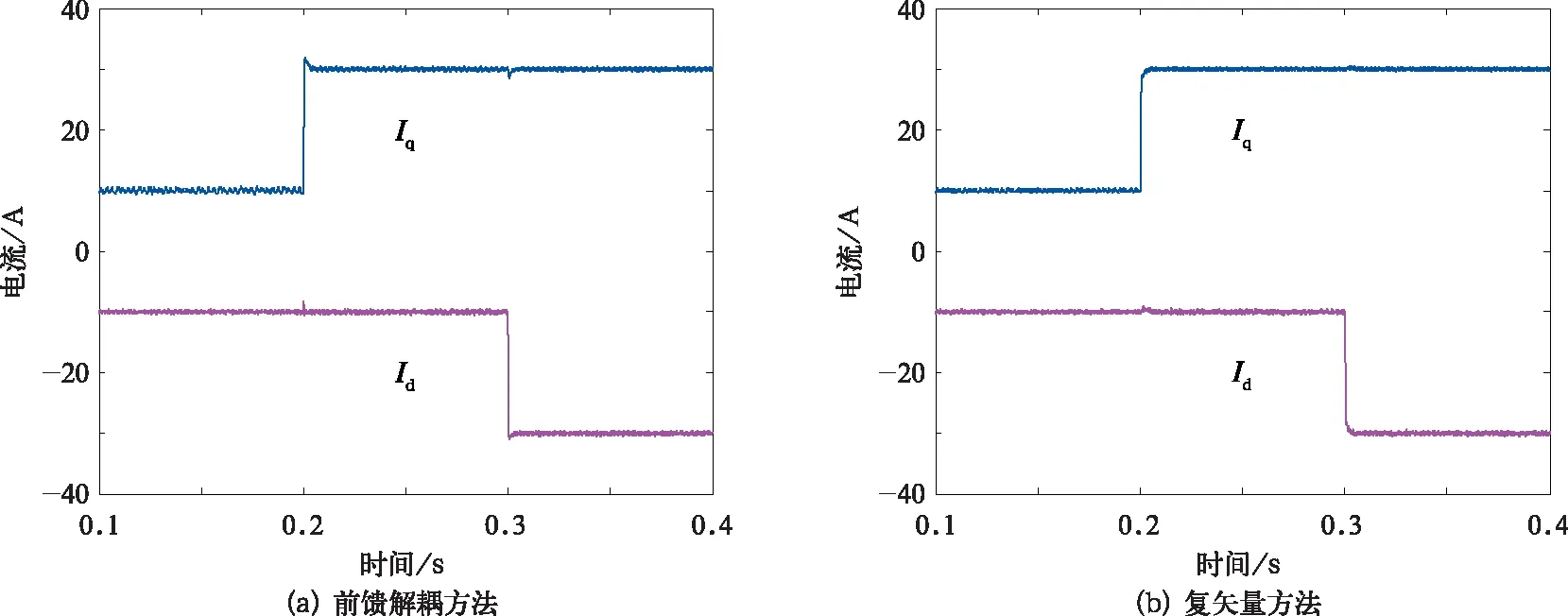
图11 2 000 r/min时两种方法动态特性仿真波形
图12 12 000 r/min时两种方法动态特性仿真波形
(1)2 000 r/min转速
图11给出了电机运行在2 000 r/min时前馈解耦PI电流调节器和复矢量电流调节器动态特性仿真波形图。0.2 s时,Iq电流由10 A阶跃至30 A,可以看出前馈解耦方法Id电流有微小波动,复矢量方法基本无波动;0.3 s时,Id电流由-10 A阶跃至-30 A,前馈解耦方法Iq电流也出现微小波动,复矢量方法也基本无波动。前馈解耦方法在低速时解耦性能虽与复矢量方法相比略有劣势,但解耦效果仍然比较理想。
(2)12 000 r/min转速
电机运行于12 000 r/min时,从仿真结果可以看出前馈解耦方法和复矢量方法的解耦效果有了明显的差异。在0.2 s时Iq电流由10 A阶跃至30 A时,Id电流随之产生较大的振荡,幅值达到10 A左右;0.3 s时Id电流由-10 A阶跃至-30 A时,Iq电流同样有较大的振荡,幅值达到5 A左右。这与上面分析一致,前馈解耦PI电流调节器特性随着电机同步频率的升高而逐渐恶化。然而复矢量电流调节器在12 000 r/min时,Id、Iq电流也能实现与低速时一样的良好解耦效果。
仿真结果证明了上面对前馈解耦方法和复矢量方法的理论分析,表明前馈解耦方法动态特性随着电机同步频率的升高而逐渐恶化,复矢量方法在任何同步频率处均有理想的动态特性。
4 结 论
文中推导了永磁同步电机复矢量数学模型,对比分析了同步旋转坐标系前馈/反馈解耦PI电流调节器和同步旋转坐标系复矢量电流调节器的控制器性能
(1) 同步旋转坐标系前馈/反馈解耦PI电流调节器在低速时解耦效果较好,但随着电机转速的升高,该控制器对电机参数的依赖性增强,解耦效果下降。
(2) 同步旋转坐标系复矢量电流调节器在任何同步频率处均有理想的解耦效果和动态特性,且对电机参数的依赖性更低。优于传统电流控制方法,为永磁同步电机控制提供了一种抗扰能力强、动态响应迅速的控制方法。

