铝合金挤压模具出口温度测量方法研究
唐秀茂,赵茂密,罗春林,冯恩浪,零妙然
(广西平果百矿高新铝业有限公司,广西531400)
0 前言
在材料加工领域,温度测量是一项极其重要的工作,但是受工作环境等条件限制,有些地方无法直接进行温度测量。比如挤压过程中型材挤出模具瞬间,由于受挤压机前梁的影响无法直接测量,特别是大型挤压机的前梁厚度大,模具出口处到前梁出口处距离更远,模具出口处的温度测量更困难。但是型材挤出模具瞬间的温度又极其重要,它直接影响产品的微观组织、表面质量、形位尺寸、力学性能等。温度过高会导致表面开裂、粗晶组织甚至过烧等,温度过低则会导致力学性能不合格、挤压力不足或模具损坏等,温度波动过大则会导致头尾微观组织、力学性能、形位尺寸等性能不均匀。目前,主流的方法是在前梁出口处通过红外测温等方法实时监控出口温度,并反馈到挤压机和铸锭加热,从而实现等温挤压[1-4]。但由于不同挤压型材截面千变万化,挤压温度及挤压速度差别也很大,该方法只能测量型材离开模具一短时间后的温度,型材在模具出口处的温度仍无法准确测量。本文通过现场测温经验,利用能量守恒定律、热量计算公式和牛顿冷却定律[5],总结出通过前梁出口温度推算模具出口温度的远程测温方法,供同行参考。
1 测量原理和方法
模具出口温度远程测量示意图如图1所示。
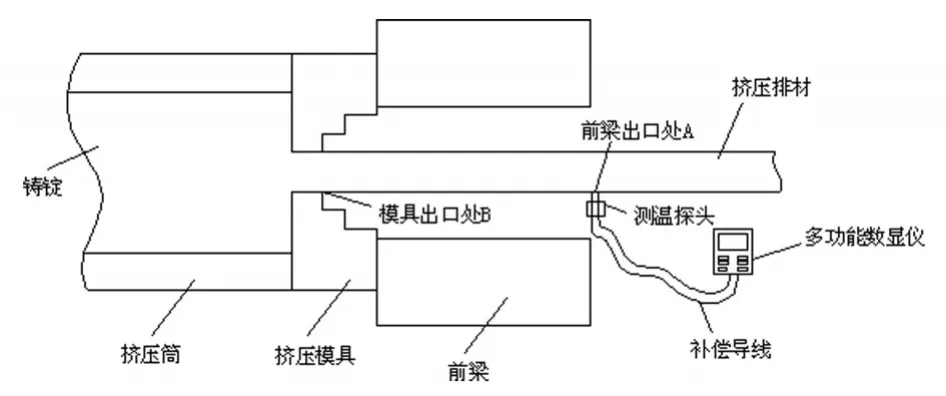
图1 测量示意图
所用的测量装置包括测温探头、补尝导线和多功能数显仪表。该测温探头通过补尝导线与多功能数显仪表进行连接。
测量原理和步骤如下:
(1)测量材料在A处的温度,在时间t内的温度变化为ΔT。
(2)根据热量计算公式设定材料放出的热量Q1=CmΔT,其中C为材料的比热容,m为材料的质量。
(3)根据牛顿冷却定律设定单位时间内材料经过对流传热散出的热量Q=hS(TA-T介),其中h为材料的表面传热系数,S为材料的表面积,TA为材料在A处的原始温度,T介为周围环境介质的温度。时间t内经过对流传热散出的热量Q2=qt=hS(TA-T介)t。
(4)根据能量守恒定律设定材料放出的热量Q1等于周围环境介质与材料表面之间对流传热的热量Q2,即Q1=Q2,即CmΔT=hS(TA-T介)t,计算得到材料的表面传热系数h=CmΔT/[S(TA-T介)t]。
(5)计算材料在B处的温度TB:材料从B处移动到A处所用时间t1内,材料经过对流传热散出的热量Q传=qt1=hS(T材-T介)t1,材料在t1时间内温度变化为ΔT1=TB-TA(在实际操作过程中,若TB小于TA,则ΔT1=TA-TB),放出的热量为Q放=CmΔT1,根据能量守恒定律Q传=Q放,得到TB=[hS(T材-T介)t1+CmTA]/Cm。
其中,t1=L/V,L为B处到A处的距离,V为材料从B处运动到A处的运动速度。
为了减少测量误差,T材取TB和TA的平均值,即T材=(TB+TA)/2,则TB=2[hST介t1-TA(hS t1/2+Cm)]/(hS t1-2Cm)。
在进行材料的温度测量前,先在测温程序中预设h=CmΔT/[S(TA-T介)t]及TB=2[hST介t1-TA(hS t1/2+Cm)]/(hS t1-2Cm)的计算公式,然后将材料的比热容C、材料的质量m、材料的表面积S、周围环境介质温度T介、材料从B处移动到A处所用时间t1录入测温程序中,再使用测温探头测量材料在A处的温度TA、材料在A处温度下降ΔT所用时间t,即可在测温程序中显示和输出材料在B处的温度TB。
2 结果和讨论
通过具体产品进行计算,以厚15mm、宽400mm的7075挤压排材在75MN挤压机上生产为例。
单位长度(1m)的挤压排材重量m=16.2kg,参与散热的表面积S=(0.15+0.4)×2×1=0.83m2(由于所测产品是连续的,所以两端的两个面不参与对流传热,只是外表面的4个面参与传热。如果是单独的整个产品,则表面积是按照6个面进行计算,即:表面积根据实际情况取值),比热容C=921J/(kg·K),周围环境介质(车间空气)温度T介=30℃=30+273K=303K,B处到A处长度L=2.7m=2700mm,挤压速度V=0.5m/min,则产品从B处运动到A处所用时间为t1=L/V=324s,设材料在B处的温度为TB,材料在A处的温度为TA。
(1)表面传热系数的计算:在A处测得产品温度TA=396.0℃=396.0+273K=669K。经过7.2s后,产品温度降低了1℃=1K,即ΔT=1;在A处测量间隔时间t=7.2s内材料放出的热量Q1=CmΔT;t=7.2s时间内经过对流传热散出的热量Q2=qt=hS(TAT介)t,由Q1=Q2及ΔT=1,得出材料的表面传热系数:
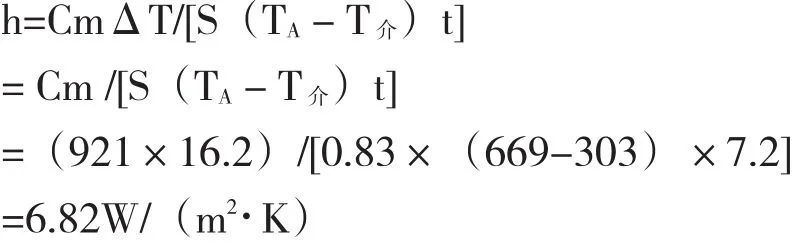
(2)模具出口温度的测量:产品从模具出口处(B处)移动到前梁处(A处)所用时间t1内,由于时间t1相对较长,材料的温度变化较大,计算表面对流传热时,为了减少误差,T材取TB和TA的平均值,即T材=(TB+TA)/2。因此,时间t1内材料经过对流传热散出的热量Q传=qt1=hS(T材-T介)t1=hS(T材-T介)L/V,材料在t1时间内温度变化为ΔT1=TB-TA,放出的热量为Q放=CmΔT1,根据Q传=Q放得出:
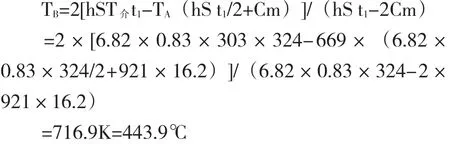
即产品在模具出口处(B处)的温度为443.9℃。
(3)本文的实验场景和测试的过程为:采用便捷式测温仪测量A处(前梁出口)的温度,通过预设了h=CmΔT/[S(TA-T介)t]和TB=2[hST介t1-TA(hS t1/2+Cm)]/(hS t1-2Cm)两个公式的远程测温程序,得出B处(模具出口)的温度。测试的过程与常规测温过程相似,不同点在于:常规测温方法只测得该处的温度,而本文通过预设计算公式可得出另一处的温度。
通过接触式热电偶实测模具出口温度进行多次测量对比,该方法与实测值偏差在±5℃以内,可以满足生产测温需求,结果见表1。其中,影响测量结果准确性的因素主要有两点:一是产品从模具出口到前梁出口的温降过程中,表面传热系数会有细小变化,而本方法假设表面传热系数为定值;二是本方法只考虑了表面传热过程,不考虑热幅射的影响。但是由于表面传热系数的变化很小,以及热幅射在整个过程的温降中所占比例极小,对本方法的影响有限,可以忽略,因此测量结果与实际相符。
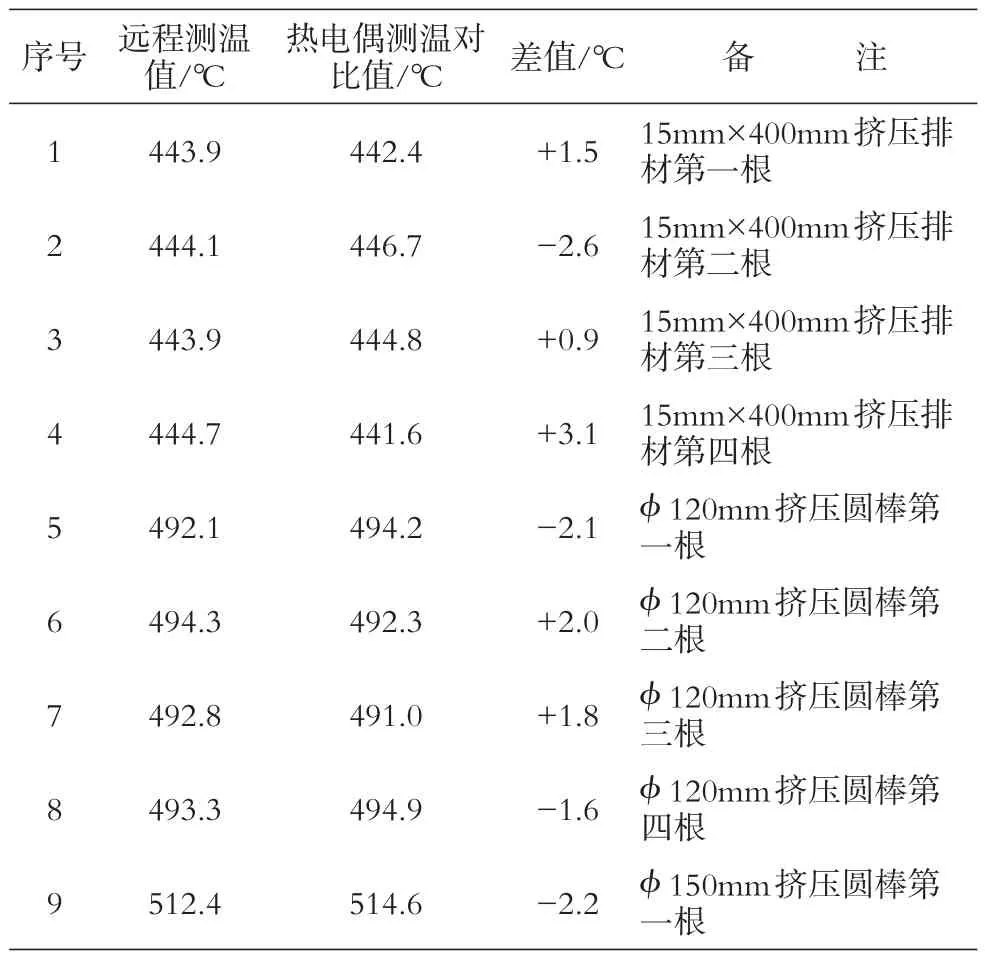
表1 远程测温与电偶实测模具出口温度结果对比
根据测量原理可知,当被测量对象的表面传热系统变化不大、且幅射传热较小,两者都可以忽略时,本文中的远程测温方法可以适用于其他材料和领域的温度远程测量。
3 结论
(1)通过测量材料在某处或某时间段的温度变化,并计算出表面传热系数,可以推算出材料在另一处或另一时刻的温度,且结果与实际相符较好,可以满足挤压模具出口温度远程测温要求。
(2)在温度测量前,先在测温程序中预设h=CmΔT/[S(TA-T介)t]及TB=2[hST介t1-TA(hS t1/2+Cm)]/(hS t1-2Cm)的计算公式,然后将材料的比热容C、材料的质量m、材料的表面积S、周围环境介质温度T介、材料从B处移动到A处所用时间t1录入测温程序中,再使用测温探头测量材料在A处的温度TA、材料在A处温度下降ΔT所用时间t,即可在测温程序中显示和输出材料在B处的温度TB。
(3) 本文所述的远程测温方法同样适用于其他材料和领域的温度远程测量。

