基于CNN噪声分离模型的噪声水平估计算法

徐少平 刘婷云 李崇禧 唐祎玲 胡凌燕

(南昌大学信息工程学院 南昌 330031)

对于图像超分辨率重建[1-2]、图像去模糊[3]、图像降噪[4-5]等各类图像复原算法来说，噪声水平值是一个至关重要的输入参数，不准确的噪声水平值会在很大程度上影响这些算法的性能.然而，大多数已提出的图像复原算法[6]都属于非盲类型的(non-blind)，即需要人工手动设置并调整相应的噪声水平值才能获得最佳的图像复原效果，这严重限制了它们的实际应用范围.因此，研究自动化的图像噪声水平评估(noise level estimation, NLE)算法是很有必要的.

现有的大多数NLE算法的核心技术路线是先将图像内容信号和噪声信号分离，然后根据分离出的噪声信号提取特征进而估计噪声水平值.例如Immerkr利用1个3×3的矩阵掩模，对图像局部邻域内的加性0均值高斯噪声求和，再根据方差估算出噪声水平值[7].虽然该算法的执行效率很高，但其噪声水平估计准确率较低；Zoran等人[8]认为图像噪声是引起边缘带通滤波器响应分布峰度值(kurtosis value)变化的主要因素，通过构建优化模型对噪声水平值进行估计.该算法在中低水平噪声条件下的估计准确度较高，但是在噪声水平较高的情况下其估计效果不理想，执行时间较长.近期Katase等人[9]提出了一种基于离散余弦变换(discrete cosine transform, DCT)系数特征的NLE算法.该算法根据DCT系数中高频部分的标准方差选取平滑的图块，利用噪声图像中的高频系数计算出噪声水平值,它在噪声水平较低的情况下性能良好，对于高水平噪声，预测效果不够理想.Rakhshanfar等人[10]根据亮度值和方差对图像分解的图块进行分类，基于噪声统计特性和图像同质区域，将与噪声模型相似程度最高的图块群(patches clusters)用于估计噪声方差.该方法可以处理多种类型图像噪声，在预测准确性表现相对良好，但是其执行效率与图像内容的复杂度密切相关.当噪声水平值较高时，执行时间显著增加.Chen等人[11]通过研究发现无失真图像中提取的图块通常位于所谓的低维子空间(low-dimensional subspace)，可以利用主成分分析(principal component analysis, PCA)方法获得冗余维度上的特征值，将其用于估计噪声方差.该算法用循环穷举的方式来确定冗余维度上的特征值，导致算法效率不高.

总体上来说，上述算法都属于所谓的基于单图像的噪声水平估计(single-image based noise level estimation，SNLE)算法.在估计噪声水平值时仅有待评价图像本身的信息可以利用，因此需要设计复杂的处理流程将噪声信号从图像中分离(提取)出来后才能进一步基于噪声信号部分进行估计，在执行效率方面并不是很理想.NLE算法作为众多图像处理算法的预处理模块，除了预测准确性外，执行效率也是重要的评价指标.近年来，笔者试图通过基于训练的方法，充分利用蕴藏在已知多幅图像中的规律性的信息，从图像中提取反映噪声水平值高低的特征值后实现快速的噪声水平映射(预测)，这种方法被称为基于多图像的噪声水平估计(multiple-image based noise level estimation, MNLE)算法.例如在文献[12]中，提出了用梯度幅值和拉普拉斯变换2种算子提取噪声水平感知特征(noise level-aware feature, NLAF)，然后基于在大量训练数据上获得的NLAF特征值以及相应的噪声水平值利用支持向量回归(support vector regression, SVR)完成预测模型的训练.预测模型所预测的噪声水平值能使BM3D(block-matching and 3D filtering)降噪算法获得最佳降噪效果.基于训练的MNLE算法的执行效率比现有经典算法具有明显优势，但是预测精度水平较主流算法尚有一定差距.提高基于MNLE算法的预测准确性需要从2个方面入手，即提取高质量的能反映噪声水平高低的NLAF特征和利用机器学习算法训练非线性映射能力更强的预测模型完成从NLAF特征值到噪声水平值的映射[12-13].

为了提取对噪声水平值更为敏感的NLAF特征，高质量地将图像内容与噪声信号分离是基础性的工作.为此，将近年来出现的非线性逼近能力强大的卷积神经网络(convolutional neural network, CNN)[14-16]技术引入到MNLE算法中来，提出一种基于CNN噪声分离模型的噪声水平估计算法.该算法利用CNN网络训练一个专门的预测模型完成将噪声信号从噪声图像中剥离出来的任务，然后利用通用高斯模型(generalized Gaussian distribution, GGD)对噪声映射图(noise mapping)进行建模并利用模型参数值作为反映图像噪声水平高低的NLAF特征值.最后利用改进的BP映射模型完成从NLAF特征值到噪声水平值的预测任务.相对于已有的各类NLE算法，所提出的NLE算法的优势主要体现在3个方面：

1) 噪声信号分离效果好.充分利用了CNN强大的非线性逼近能力，在已知噪声水平下的样本图像集合中学习先验知识，高质量地将噪声信号从噪声图像中分离出来，为构建高敏感度的NLAF特征打下了很好的基础.

2) NLAF特征到噪声水平的映射能力强.采用改进的BP神经网络技术获得了比常规SVR支持向量回归映射更高的预测正确率.

3) 执行效率高.改进算法的特征值提取和噪声水平值的映射工作是由CNN和改进BP(back propagation)神经网络来完成的.一旦训练完成，其执行效率非常高，尤其是CNN卷积网络在GPU(graphics processing unit)硬件支持下运行时间很短，几乎可以忽略.

1 CNN简介

(1)

在卷积层中，用滤波器与上一层若干个特征映射图(feature map)进行卷积，计算出新的特征映射图，通过激活函数将特征保留并输出到下一层结构.近年来研究者们主要采用修正线性单元(rectified linear unit, ReLU)[19]作为激活函数，其数学形式表述为ψ(x)=max(x,0)，将负值置0.ReLU能够加快整个网络的收敛速度，而不影响卷积层的感受野(receptive field)，大大提高了激活函数的性能[20].卷积后产生q维的特征映射图(feature map)

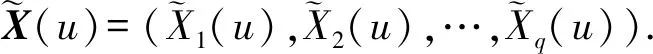
(2)

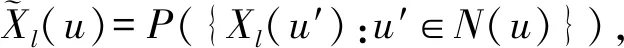
(3)

其中，l=1,2,…,q,N(u)是u的邻域，P是某种类型的池化函数(可以是最大值、均值等类型).基本的CNN卷积神经网络可以表示为卷积层和可选的池化层的多次组合，即

ΦH(X)=(CH(K)…P…∘CH(2)∘CH(1))(X),

(4)

其中，P为可缺省的池化操作，H=(H(1),H(2),…,H(K))是网络参数(卷积核的系数值)的超矢量(hyper-vector).通常，在卷积神经网络中的卷积层或者池化层之后可以连接全连接层(fully connected layer)，全连接层在整个CNN中用来获得特征，为后面的分类或者回归任务做准备.另外，为了减少内部协变量转移对网络参数的影响，批归一化层(batch normalization, BN)[21]常被用来对卷积神经网络隐藏层的输出数据进行批归一化处理，从而加快神经网络的收敛速度并获得稳定性.

2 基于噪声分离模型的NLE算法

2.1 NLE算法的基本思想

如图1所示，改进算法技术路线的关键之处在于：首先高质量地将噪声图像的内容信号与噪声信号进行分离获得噪声映射图;进而基于噪声映射图提取NLAF特征;最后通过训练学习获得映射能力强的预测模型将NLAF特征准确地映射为噪声水平值.具体地，在训练阶段：1)选择大量具有代表性的自然图像添加不同噪声水平的高斯噪声获得噪声图像集合，噪声图像、无失真图像、噪声图像与无失真图像相减获得的噪声映射图以及对应的噪声水平值构成训练数据集合;2)通过训练CNN网络在噪声图像和噪声映射图之间构建CNN噪声分离模型，利用该模型即可完成将噪声信号从噪声图像中剥离出来的任务;3)分离噪声信号后，采用GGD模型对噪声映射图进行建模并利用模型参数值作为反映图像噪声水平高低的NLAF特征值;4)基于从训练集中的噪声图像上提取出的特征值及相应的真实噪声水平值，训练改进的BP映射模型完成从NLAF特征值到噪声水平值的预测任务.在预测阶段:1)将噪声图像输入到CNN噪声分离模型分离出噪声映射图;2)用GGD特征提取模型提取其NLAF特征并由改进的BP映射模型最终映射为噪声水平值.

Fig. 1 The overall framework of the proposed method图1 改进算法流程框图

2.2 分离噪声信号

本文主要工作是利用CNN网络强大的学习能力，达到从噪声图像中分离出噪声信号的目的.一般来讲，受到噪声干扰的图像的数据模型可以定义为

y=x+n,

(5)

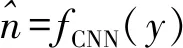
基于上述设计需求，与一般利用CNN卷积神经网络完成分类或者回归任务不同，所提出的算法需要基于输入的噪声图像各个像素点的亮度值得到对应像素点的噪声值，故输入模型的图像大小和输出图像的大小相同.因此，所设计的CNN卷积神经网络中不使用池化层和全连接层结构，仅包括卷积层、BN和ReLU共3种类型的网络部件，具体结构如图2所示.从图2中可以看出，网络从左到右共分3段：

1) Conv+ReLU.第1段用64个大小为3×3的卷积核生成64个特征图像.

2) Conv+BN+ReLU.第2段与第1段的区别是使用了BN批归一化层，使用BN层的目的是为了保证每一层网络的输入具有相同的分布、加快训练进程并提高噪声水平预测准确率.

3) Conv.最后1段采用1个大小为3×3×64的卷积核来输出噪声映射图.

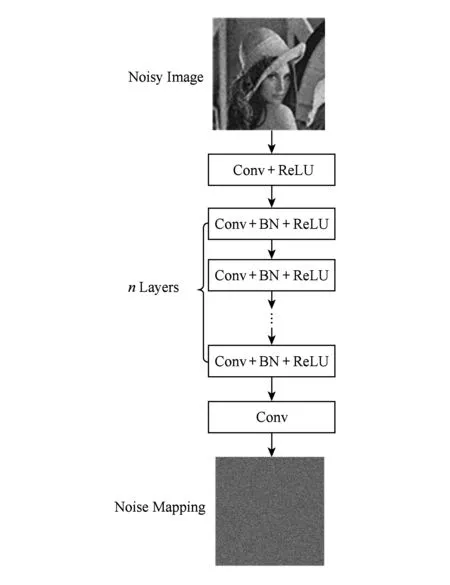
Fig. 2 The network architecture of CNN-based noise separation model图2 CNN噪声分离模型的网络体系架构图

2.3 噪声映射图与GGD建模

为了验证卷积神经网络对噪声图像中的噪声信号部分的实际分离效果，以1幅512×512大小的Lena图像为例，对其分别添加噪声级别为5，10，20，40，50的高斯噪声，然后利用所提出的CNN分离模型将噪声信号分离出来得到噪声映射图，计算噪声映射图中系数值分布情况，系数分布直方图如图3所示(为了便于显示和比较，图3中的横坐标值所代表的残差系数值(噪声值)被归一化到[-1,1]之间，而纵坐标则是像素点个数除以1 000以后的结果).由图3可知，噪声映射图的系数值分布具有显著的类高斯分布特征，可用GGD广义高斯分布对噪声映射图进行建模.

Fig. 3 The distribution histogram of coefficient values图3 系数值分布直方图

GGD模型[22]是一种应用非常广泛的分布模型，一般定义为

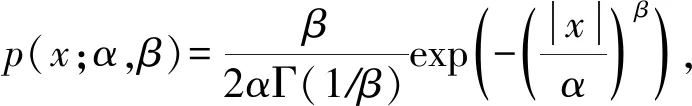
(6)

其中，Γ(·)是Gamma函数，即:

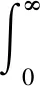
(7)

式(6)中的α为尺度(scale)参数，控制着GGD密度函数的扩散程度.β为形状(shape)参数，用于修正峰度值的衰减速度.参数α和β与GGD分布的标准差σ满足关系式:

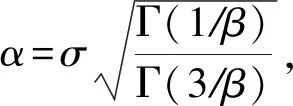
(8)

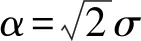
2.4 噪声水平感知特征选取

用GGD模型为噪声映射图系数值分布建模后，模型中共有2个参数，即α和β.为了测试模型中的2个参数是否能够作为NLAF特征值使用，用GGD模型为图2中5个级别的噪声映射图建模，所提取的模型参数如表1所列.从表1中可以看出：α参数值与相应噪声水平值之间的Pearson线性相关系数(Pearson linear correlation coefficient, PLCC)为1，表明这2者之间具有极强的相关性；β参数值与相应噪声水平值之间的PLCC系数为0.649 6，表明这2者之间的相关性处于中等水平.为了全面验证该参数是否与噪声值具有强相关性，在100幅图像上执行与图2相同的处理过程并提取GGD模型的2个参数值，再计算它们分别与真实噪声水平值之间的PLCC相关系数.经计算，α值与真实噪声水平值的线性相关系数为0.998 7，继续保持非常高的相关性.而β值与真实噪声水平值的线性相关系数为0.668 3，有所提高但仍然处于中等水平.为了获得鲁棒的噪声水平值，将参数值α和β组合作为NLAF噪声水平感知特征矢量F=(α，β)来使用.

Table 1Correlation Coefficients Between the Noise Levels andParameters of GGD Model

表1 GGD参数值与噪声水平值的相关系数

2.5 改进的BP神经网络

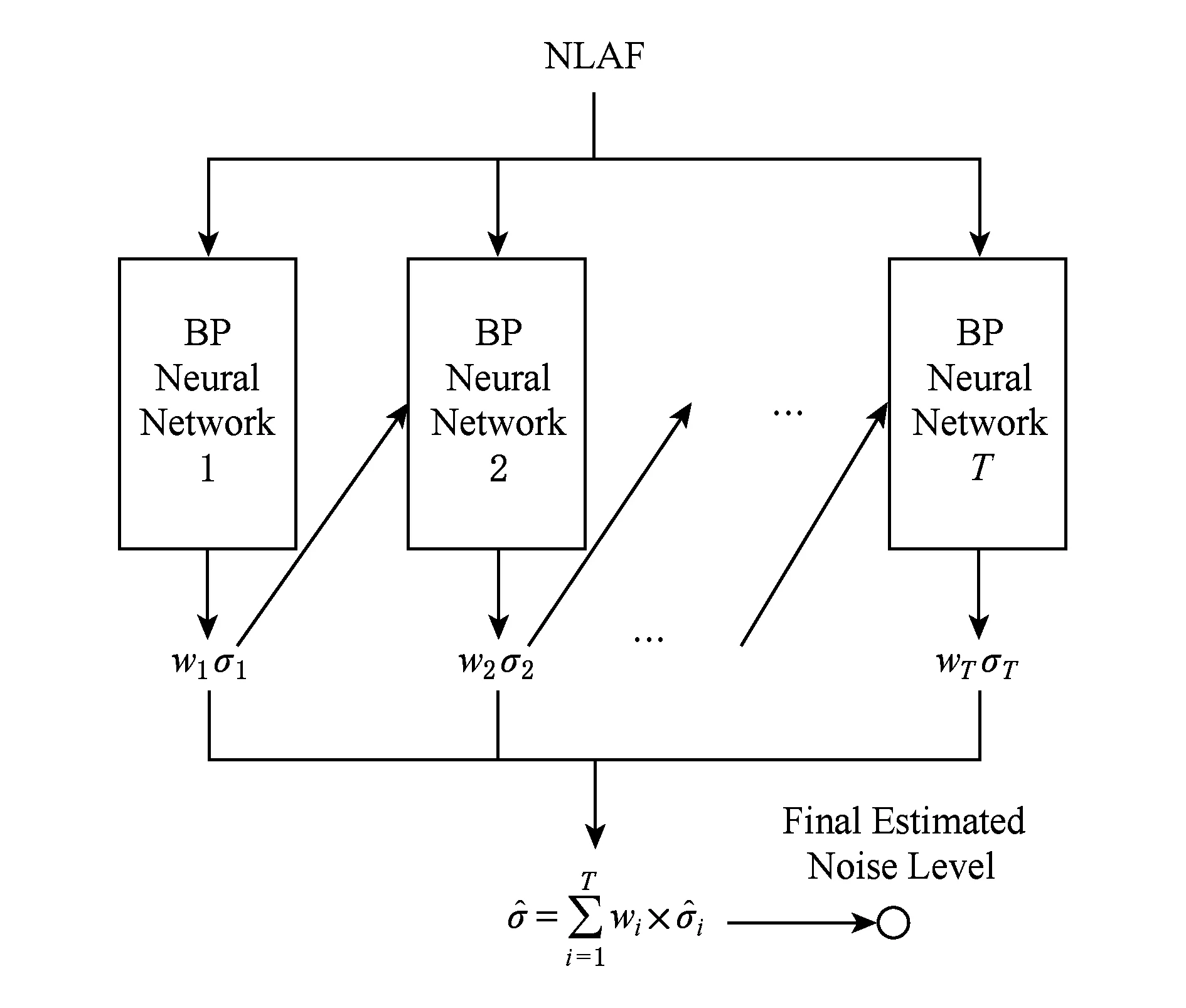
Fig. 4 Pipeline of the improved BP neural network图4 改进BP神经网络工作原理

用GGD模型在大量训练图像上提取噪声映射图的特征值后，理论上即可利用任何回归分析技术将特征值(构成矢量形式)映射为最终的噪声水平预测值(标量).由于所使用的特征值只有2维，维数较少，利用常规的SVR构建预测模型的预测准确性不是很理想.如图4所示，为了进一步提升预测准确性，首先利用若干个BP网络构建预测能力相对较弱的弱预测器，然后利用AdaBoost算法[23]在多个弱预测器的基础上构建比较健壮、准确的强预测器.AdaBoost算法原本的设计思想是利用若干个弱分类器构建强分类器的分类问题，这里将其运用到回归问题中来，所用的预测模型称为改进的BP映射模型.

选取K幅图像进行训练，对每幅图像添加已知噪声水平值为σi的高斯噪声，用GGD模型提取对应的特征矢量Fi(其中i=1,2,…,K)构成训练集合{(F1,σ1),(F2,σ2),…,(FK,σK)}⊂R2×R，训练出预测函数φ(·)以实现特征矢量到噪声水平值之间的映射.改进BP映射算法的具体执行过程如下：首先，确定弱预测器的数量(根据实验数据T=5时，已能满足精度要求且同时兼顾执行效率).从第1个弱预测器开始，利用BP神经网络建立特征矢量Fi和噪声水平值σi之间的映射关系，第j条训练数据对预测结果的权重更新方法为

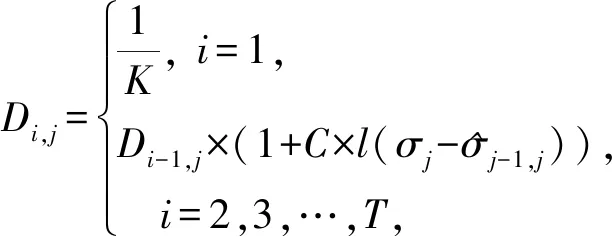
(9)

其中，Di,j代表在第i个弱预测器中第j条训练数据对预测误差的权重，C为[0,1]之间的常数.对于第1个弱预测器来说，各个训练数据的权重初始化为1K，从第2个弱预测器开始，则根据前一个预测器预测结果的误差利用二值函数(binary function)

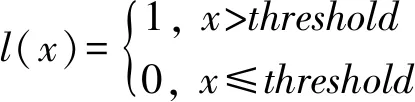
(10)

进行修正.根据实验数据，设定参数C=0.1，threshold=0.1.第i个弱预测器整体的预测误差可以定义为用第i个预测器所预测的噪声估计值与真实噪声水平值之间的差值和训练数据权重乘积的累积和，从数学形式上描述为

(11)

利用凸函数将每个弱预测器的预测误差转换为弱预测器在最终预测结果中的权重.这样使得那些预测误差较小的弱预测器的权重增加，而误差较大的弱预测器的权重减小.第i个弱预测器的权重定义为

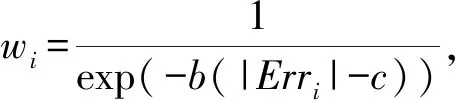
(12)

(13)

实验数据表明使用过多或者过少的弱预测器都将导致预测准确性下降.另外一方面，随着使用更多的弱预测器，执行效率也将随之下降.文中最终使用5个弱预测器构建改进的BP映射模型，在这个配置下能在预测准确性和执行效率这2个方面获得最佳平衡点(限于篇幅，这里不再给出具体实验数据).综上所述，基于多个BP网络模型利用AdaBoost算法提升预测准确性的伪代码描述如下：

算法1.改进BP神经网络模型训练过程.

输入：训练图像集{(F1,σ1),(F2,σ2),…,(FK,σK)}⊂R2×R；

输出：各预测器模型{BPi|1≤i≤5,i∈N+}及对应的权重值w={w1,w2,…,w5}.

① 初始化基于BPi网络的弱预测器的分布D1,j、计算对应的估计误差Err1及权值w1；

② fori=2,3,…,5

③ 根据式(11)计算第i个弱预测器BPi的估计误差Erri；

④ 根据式(9)计算第i个弱预测器BPi的分布Di,j；

⑤ 根据式(12)计算第i个弱预测器BPi的权值wi；

⑥ 归一化弱预测器的分布Di,j；

⑦ end for

⑧ 输出各个BP预测器并归一化它们的权值.

3 实验与分析

3.1 测试环境

从BSD(Berkeley segmentation dataset)数据库[24]中随机选取了100幅图像，对这些图像添加51个级别(0,1,…,50)的高斯噪声作为训练图像集合，基于训练图像集合训练预测模型.测试图像集包括2个：第1个由在各类图像处理相关文献中常用的10幅图像组成，如图5所示；为了增加测试难度，在BSD数据库另选了与训练集合不同的50幅纹理图像构成第2个测试集合.BSD数据库原本作为纹理分割的基准测试数据库，其图像中的纹理细节非常丰富，很多NLE算法的性能在该数据库上表现不佳，比较适合用来作为测试图像集合.参与比较的NLE算法包括Immerkr算法[7]、Zoran算法[8]、Liu算法[25]、Chen算法[11]、Rakhshanfar算法[10]和Xu算法[1]，其中Xu算法是笔者之前基于主成分分析和SVR实现的NLE算法.为了验证改进的BP映射模型的性能，本文对比了4种从NLAF特征到噪声水平值的映射模型.其中，直接利用常规SVR和BP构建映射模型的NLE算法分别记为CNN+SVR和CNN+BP；基于SVR和BP利用AdaBoost算法改进的映射模型实现的NLE算法分别记为CNN+AdaSVR和CNN+AdaBP，这样共有10个NLE算法参与对比实验.通过比较以上各个算法在不同噪声水平下的噪声估计准确性以及执行时间，来测试所提出算法的综合性能.实验在Matlab R2017b(运行在Intel®CoreTMi7-6700 CPU RAM 8 GB主机上)环境下完成.

Fig. 5 Commonly used images in the literature图5 各类文献中常用的图像集合

3.2 预测准确性

在常用图像集合中的图像上施加噪声级别为5～50、间隔为5的噪声，统计各对比算法在每幅图像上的预测结果，以噪声水平预测值与真实值之间的绝对偏差值作为衡量算法预测准确性的指标.限于篇幅，这里仅给出在Couple图像的预测结果，预测结果排名前3的算法加粗标出，准确性最高的另用下划线标出.由表2可知，Immerkr算法、Zoran算法、Chen算法、Xu算法、CNN+SVR算法和CNN+AdaSVR算法在Couple图像上的预测结果较其他对比算法还不够理想；Liu算法、Rakhshanfar算法、CNN+BP算法和所提出的CNN+AdaBP算法在各个噪声级别下表现出良好的预测准确性.从整体上看，Rakhshanfar算法的预测准确性在不同噪声水平值上变化较大，稳定性较差；Liu算法在各噪声水平下尤其是低水平噪声条件下预测性能最好，但Liu算法是以执行时间为代价才获得高准确性的.CNN+BP算法和CNN+AdaBP算法的预测准确性与Liu算法的相差不大，但执行效率则具有显著优势，因此所提出的CNN+AdaBP算法综合性能更好.

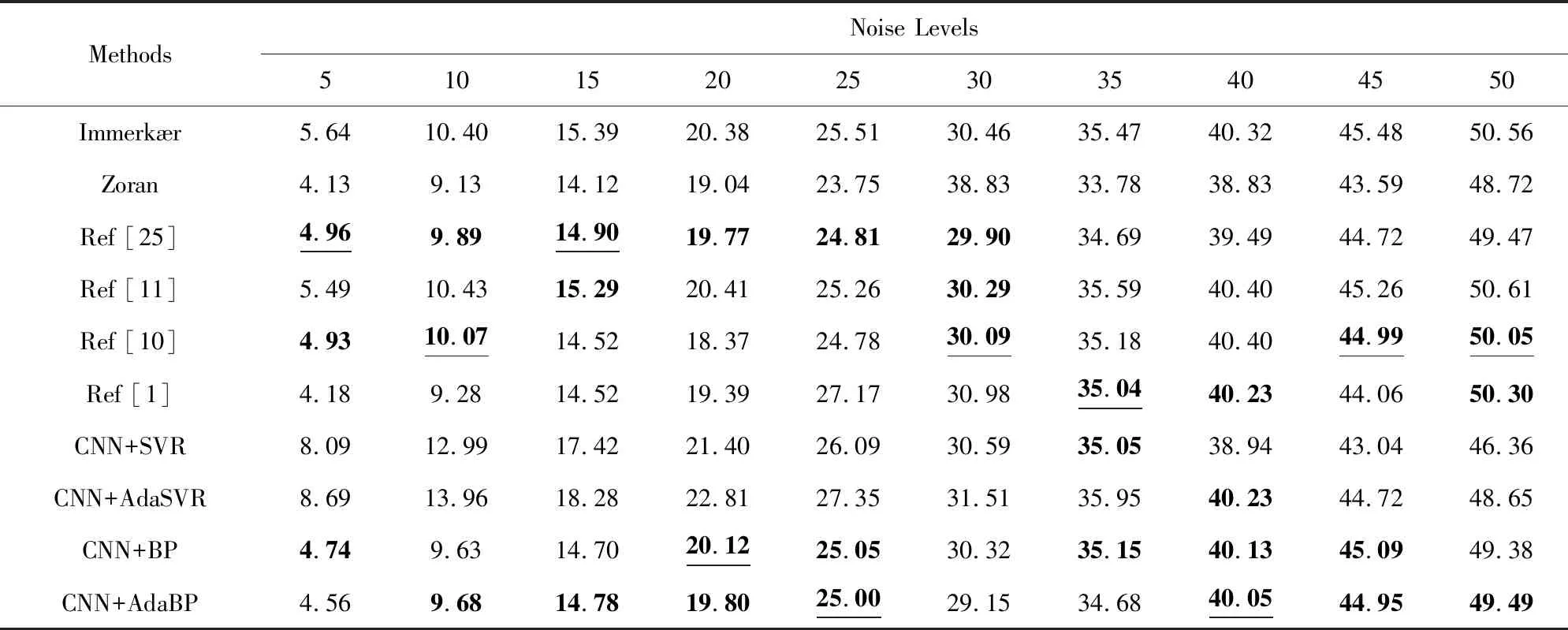
Table 2 Estimation Results Obtained with Different Algorithms on Couple Image at Different Noise Levels表2 不同噪声水平下各算法在Couple图像上的评估结果

Note: The top 3 results are bold, and the best values are underlined.

在单幅图像上的噪声水平估计值的对比并不能全面地评价某个算法的鲁棒性.因此，对于图5中的10幅测试图像，计算各个算法对它们噪声水平的估计值与真实值之间的均方根误差(root mean squared error, RMSE)，结果列在表3中.在各噪声水平下，前3个最好的算法加粗标出，最小的RMSE值另用下划线标出.从表3中的数据可以看出：各算法性能与在单幅图像上情况近似，CNN+SVR和CNN+AdaSVR算法的预测准确性比较差，未进入前3名，这说明SVR不适合用于完成噪声水平值的映射任务，而Adaboost技术也不能显著提高SVR的映射能力；Liu算法、CNN+BP算法和CNN+AdaBP算法的均方根误差排名前3，其中Liu算法在低噪声水平条件下的均方根误差非常小(以执行时间为代价)，在中高噪声水平条件下的均方根误差相对于低噪声水平却要大许多，稳定性不够好；CNN+BP算法整体上均方根误差的平均值比CNN+AdaBP算法稍差.CNN+AdaBP算法在各个级别的噪声条件下的均方根误差都比较小，且预测准确性比较稳定.这说明了CNN+AdaBP算法利用Adaboost技术提升BP映射模型的性能是成功的，这是因为CNN+AdaBP算法中BP网络弱预测器本身具有一定的预测能力，且适当个数的弱预测器之间能形成互补，在Adaboost框架下组合利用多个BP弱预测器后其预测准确性得到进一步提升.

Table 3 RMSE Between Estimated Results and Ground Truths on Ten Commonly Used Images表3 各算法在10幅常用图像集合上预测结果的均方根误差

Note: The top 3 results are bold, and the best values are underlined.

Table 4 RMSE Between Estimated Results and Ground Truths on Fifty Images from BSD Database表4 不同噪声水平下不同算法在50幅BSD图像上预测结果的均方根误差

Note: The top 3 results are bold, and the best values are underlined.

为了验证算法对测试图像的鲁棒性，随机选取了BSD数据库50幅图像作为测试集，分别给图像加入级别为5～50、间隔为5的高斯噪声，并计算各个算法预测结果与真实值之间的均方根误差，列在表4中(排名标记方法与上文相同).由表4中可知：各个算法的预测准确性在难度很大的纹理图像上有所下降，但是排名情况总体与表3类似，所提出的CNN+AdaBP算法仍然具有最好的性能.

为了验证CNN+AdaBP算法的泛化能力，对BSD数据库中的50幅图像添加2.5，7.5，12.5，17.5，22.5，27.5，32.5，37.5，42.5，47.5这10个在训练模型时未用到的噪声水平值，并计算对应的均方根误差，结果如表5所示.

从表5可以看出：所提出的CNN+AdaBP算法能够很好地预测噪声级别在0～50之间的任意噪声水平值，且算法的预测准确性足够稳定.综上所述，CNN+AdaBP算法具有良好且稳定的预测准确性，其原因在于该算法是根据自然图像统计规律在大量自然图像上训练学习获得的.

Table 5 RMSE of the Estimated Results at Different Noise Levels

3.3 BM3D算法降噪

为了进一步验证CNN+AdaBP算法的实际应用效果，用经典BM3D降噪算法对分别加入不同噪声级别的Lena图像进行降噪，表6列出了分别使用真实噪声水平值和根据CNN+AdaBP算法预测出的噪声值作为BM3D算法的输入参数进行降噪后的图像的峰值信噪比(peak signal to noise ratio, PSNR).

Table 6 PSNR of Image Denoised by BM3D Algorithm Using Ground Truth and Estimated Noise Levels表6 BM3D分别使用真实噪声值和预测噪声值的降噪结果 dB

从表6中的数据可以看出，使用CNN+AdaBP算法预测出的噪声水平值作为参数的降噪效果与使用真实噪声水平值作为参数的降噪效果差别很小，这充分说明了CNN+AdaBP算法的实用性和有效性.

3.4 执行时间的对比

对于一个图像噪声水平估计算法来说，不应仅仅根据算法的预测准确性来评判该算法性能是否良好，执行效率也是非常重要的评价指标.为了充分证明所提出的算法性能良好，笔者对各个算法的执行时间进行了比较.将各算法在1幅大小为512×512的Lena图像上重复执行20次，计算算法估计该图像噪声水平值的平均执行时间，各算法在不同噪声级别下平均执行时间如表7所示.从表7可以看出：Zoran算法和Liu算法的执行时间非常长，不适合应用于时间要求比较严格的系统中.相比而言，Chen算法和Rakhshanfar算法的执行效率一般.由表2～4中的数据可知，这2个算法的预测精度也一般.Immerkr算法和Xu算法的执行时间非常快，但是从表3～4中的数据可知，这2种算法的评价准确性比较其他算法要差一些.CNN+SVR算法、CNN+AdaSVR算法、CNN+BP算法和CNN+AdaBP算法作为基于训练的MNLE算法，模型一旦训练完成，执行速度处于所有参与比较算法中的前列.综上所述，所提出的CNN+AdaBP算法在预测准确率和执行效率这2个方面的综合性能较其他算法更优.

Table 7 Average Execution Time of Different NLE Methods at Different Noise Levels表7 各算法在不同噪声级别下的平均执行时间 s

4 总 结

传统基于单幅图像的SNLE算法中将图像内容与噪声信号分离的关键模块在算法设计上比较复杂，导致执行效率比较低.为此，提出了一种利用CNN在多幅图像上通过训练学习实现快速分离噪声信号获得噪声映射图的新方法.然后，利用广义高斯分布GGD模型为噪声映射图建模，并以模型参数值作为反映噪声严重程度的NLAF特征值.最后，训练改进后的BP网络模型实现从NLAF特征值到噪声水平值的预测任务.与现有的算法相比，CNN+AdaBP算法从提取高质量的NLAF特征和构建非线性映射能力强大的映射模型2个方面入手，在保持高效率的前提下，进一步提高了MNLE这类算法的预测准确率，获得了一种预测准确性和执行效率的综合性能更好的噪声水平评估算法.