基于地震波速度预测岩体物性参数模型与应用
王大兴,赵兴华,孟凡彬,郎玉泉
(1.长庆油田分公司勘探开发研究院,西安 710018; 2.中国煤炭地质总局地球物理勘探研究院,河北涿州 072750)
0 引言
随着煤田物探装备及新一代计算技术的发展,为地震信息应用于煤系沉积岩石物性参数研究创造了条件,有助于提高对煤系沉积岩石岩性特征的认识[1]。地震勘探成果表明地震信息对于指导煤矿安全生产具有十分重要的作用,地震信息的应用不仅提高了煤层构造的解释精度,也为煤矿瓦斯预测、煤层底板突水性评价、以及煤巷岩性及其物性性质特征的研究提供了技术保障。如何把地震波捕捉到的海量地震信息和实际地质信息建立联系,成为解决煤矿地质的关键。搭建这个桥梁,就能为智能化预测煤矿地质参数打下基础,也为建立海量的煤矿物性大数据提供基石[2-4]。
本文从理论模型和相关试验为出发,通过研究地震属性及地质测井资料,提出了以地震属性、钻孔测井参数和超声波试验为基础,以数学地质为桥梁,实现煤层顶底板岩石弹性参数定量预测的科学方法并将该方法应用于实际煤田地震勘探中,取得了很好的效果。
1 地震波速度的提取
地震波速信息在煤矿地震资料研究中至关重要,它是煤矿地质体尺度研究的主要参数之一。因此,地震波速度的建立准确与否是煤矿地震资料研究的关键,决定着煤矿地质体尺度的准确性。由于煤矿顶底板围岩的复杂性,准确建立地震波速度信息项技术难度较大。岩石的地震速度主要依据实验室通过岩样标本试验测试、钻测井资料中曲线声波时差以及人工地震数据信息等三种方式获得。前两种方法是点信息,信息量少,无法满足三维空间的速度要求;而第三种方法,是在三维空间数据基础上获得速度,信息量大。对准确的点信息和体数据信息进行综合分析,可以大大提高数据分析的可信度与精确度,从而达到预测地质体岩性数据的精度[5-7]。
2 理论模型及岩石物性参数
速度是弹性波传播的基础参数之一,利用地震波速度去认知岩体的完整性及物性参数特征,能够提高研究的精度。无论是反射波、透射波和还是折射波,其在地层中传播的速度决定于岩石的弹性常数和密度。基于均匀、各向同性和完全弹性介质的地震波,其传播遵循下列方程:

(1)
在理想介质下,岩体中物性参数与岩体的纵横波速度之间存在如下关系:
(2)
(3)
其中,ρ为岩石的密度;E,σ为弹性模量和泊松比系数。对比(2)、(3)公式,显然有υP>υS。在流体介质中,υS=0,所以横波的传播与纵波不同,它不受岩石在孔隙中充填的流体的影响。(2)式、(3)式相除得:
(4)
如果υP、υS已知时,可由上式解得:
(5)
由公式:
(6)

在岩石这个介质中,物性参数主要包括杨氏模量(E)、泊松比(σ)、切变模量(μ)、体积模量(K)与拉梅常数(λ),其是分辨岩性的基础参数,其中,E和σ是常用的二个弹性参数。在一定物理环境下,已知VP、VS和密度(ρ),岩石其它的物性参数可根据公式计算出来[8-9],而在实验室测量岩石的物性参数中,σ是非常重要的参数,其与VP、VS对解释煤层顶底板物性参数至关重要。
3 岩体物性参数试验
3.1 岩体纵、横波速
岩石介质的密度和物性参数是岩石的固有属性,他们的不同,意味着地震波传播速度的不同。如公式(4)所表达的,岩石纵波的传播速度大于横波,在同一介质中纵波速度约为横波速度的1.414~1.732 倍。在液体气体介质中,切变模量μ=0 ,因而横波速度为零即意味着横波只存在于固体介质中[7]。通过对淮南、铁法等矿区87个煤系沉积岩石的岩样获得的实验数据分析,可知沉积岩石的横波速度(υS)与纵波速度(υP)与之间呈现出很好的正相关性,纵波速度越大,横波越大。其关系式为[8-9]:
υs=0.56υP+192.74,R=0.98
(7)
3.2 岩石密度与声波速度
当今国内外很多学者的研究成果认为岩石的波速和密度之间一般都是正相关关系,大多学者选择用线性函数来表示他们的关系。由于煤系沉积岩石在成分、结构和构造以及成岩作用的不同,导致岩石密度的差异,不同密度的岩石具有不同的声波速度。实验结果统计表明,煤系岩石密度ρ(g/cm3)与其声波速度之间为非线性正相关关系,它们之间的关系可表示如下[8-9]:
(9)
3.3 动、静弹性力学参数
岩体的动态弹性模量和静态弹性模量是岩体在两种不同外力作用下的力学参数[8]。岩石的弹性模量和泊松比可以由静态载荷试验和动态方法获得。动弹性力学参数是在实验室内获取超声波在岩样中的传播速度计算得来的;静弹性力学参数是在静荷载作用下获取横向和纵向变形数据,进而计算其静弹性力学参数(E,μ)[10-16]。动、静弹性力学参数试验获取的岩石静弹性参数一般要小于动弹性参数,也就是静弹性模量与静泊松比要小于其动弹性模量与动泊松比,这是由于采用动态方法测试时岩样处于完全弹性状态所致。本次试验数据结果表明它们之间呈线性相关关系,沉积岩石动弹性模量与静弹性模量之间的线性回归方程为[8-9]:
Ed=0.763 2Es+22.604
(10)
式中:Ed为动弹性模量(GPa);Es为静弹性模量(GPa);相关系数R=0.87,统计数N=47。
沉积岩石动泊松比与静泊松比之间的线性回归方程为[8-9]:
μd=0.289 9μs+0.1366
(11)
式中:μd为动泊松比;μs为静泊松比;相关系数R=0.61,统计数N=21。
3.4 岩石单轴抗压、抗拉强度与声波速度
试验研究表明,煤系岩石力学参数与其纵波或横波速度具有较好的相关性,随着纵波或横波速度的增加煤系岩石的单轴抗压强度和抗拉强度也增大,试验成果分析可知,煤系岩石单轴抗压强度与其纵波或横波速度之间具有如下指数关系:
(12)
式中:Rc为煤系岩石单轴抗压强度(MPa);
试验成果分析可知,煤系岩石单轴抗拉与其纵波或横波速度之间具有如下线性相关关系:
(13)
式中:Rt为煤系岩石单轴抗拉强度(MPa);
3.5 波速与孔隙度
近年来,有一系列论文讨论纵横波速度与孔隙度关系,方法众多,但得出的结果比较类似。本文采用的是Castagna等从测井数据数据推导出的波速与孔隙度的关系式[13]:
φ=0.823 7-0.567 9υp+0.615 2υs
(14)
4 应用
淮南煤田刘庄区为一全隐蔽煤田,地形平坦,其构造单元隶属淮南复向斜中西部的次一级褶皱——陈桥背斜之南翼,为一轴向北西西向的不完整且略有起伏的宽缓向斜。向斜北翼地层倾向南,倾角10°~20°,向轴部逐渐变缓。F14断层以西倾斜。南翼有区域性F1断层,并形成叠瓦式构造,使老地层推复到煤系地层之上。另外,工区东西两侧受F5、F12边界断层影响,从东到西分为三个块段。
通过整理刘庄区13口地震测井资料,与实验室测试数据相比,测井资料所得到的岩石物性参数更能反映其在地层状态下的实际特征,采用速度标定的方法获得区内钻孔层间速度参数。依据全区所有钻孔求得的速度参数,结合地震信息和测井信息勾制平面速度分布图,从而更精确地描述速度参数在三维空间的变化(图1)[17]。
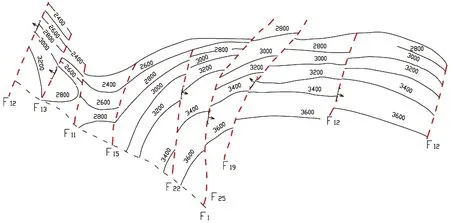
图1 刘庄区T0速度分布图Figure 1 T0velocity distributions in Liuzhuang area

图2 刘庄区岩层密度分布图Figure 2 Rock density distributions in Liuzhuang area
由图1和公式(8)、(9)可分别求出横波速度(υS)和密度(ρ),进而可生成其密度变化分布图(图2)。
在煤矿开采中,准确的岩石力学数据,对巷道的工程施工、煤矿深部地质力学研究具有指导意义[15-16];由纵波速度(υP)、横波速度(υS)和密度(ρ)可分别求出其余的岩石物性参数。参考国内外众多学者的最新研究成果,预测的相关成果如表1及图3—图8。
从上述成果图中可知,该地区的各个物性参数的分布规律明显,证明地震信息预测岩石力学参数的方法具有可行性。依据淮南煤田刘庄区地震勘探数据对该区岩石物性参数进行综合分析,结果表明其计算的物性参数与实测结果吻合较好。
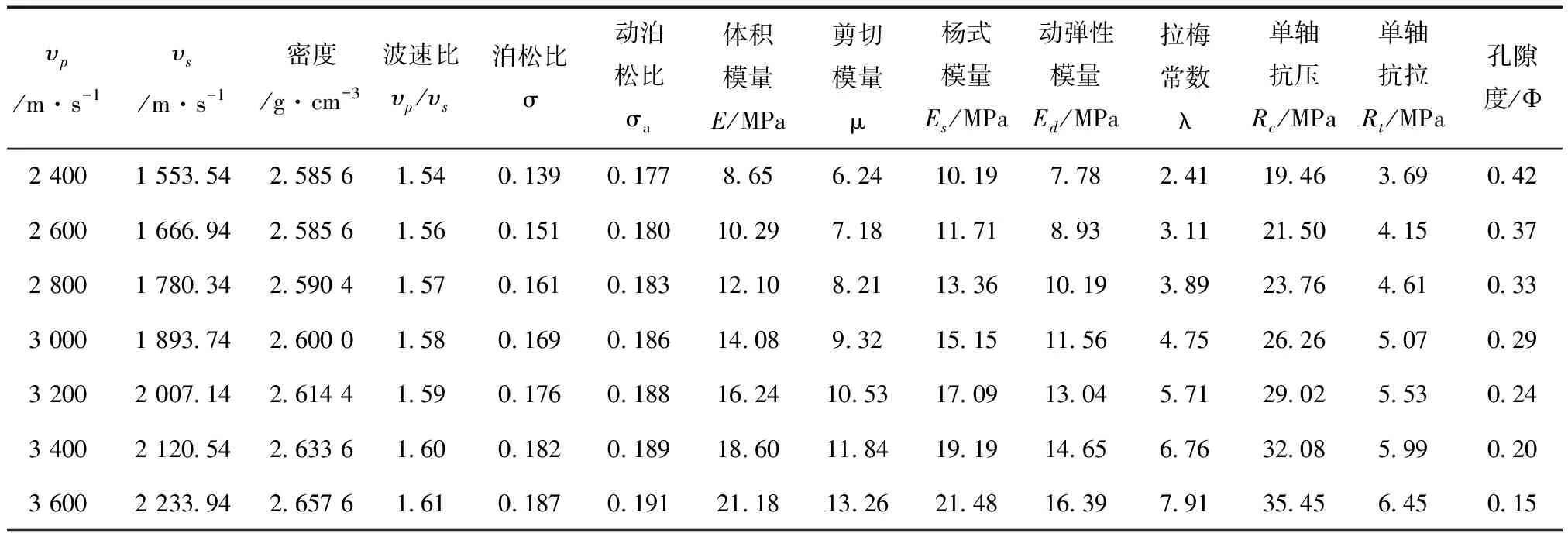
表1 刘庄区煤层顶底板岩体物性参数计算值

图3 刘庄区动泊松比分布图Figure 3 Dynamic Poisson's ratio distributionsin Liuzhuang area

图4 刘庄区体积模量分布示意图Figure 4 A schematic diagram of bulk modulus distributionsin Liuzhuang area

图5 刘庄区动弹性模量分布示意图Figure 5 A schematic diagram of dynamic elasticity modulusdistributions in Liuzhuang area

图6 刘庄区单轴抗压强度分布示意图Figure 6 A schematic diagram of uniaxial compressivestrength distributions in Liuzhuang area

图7 刘庄区单轴抗拉强度分布示意图Figure 7 A schematic diagram of uniaxial tensile strengthdistributions in Liuzhuang area
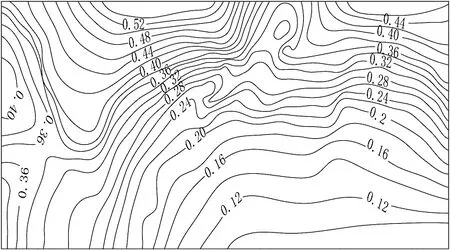
图8 刘庄区孔隙度分布示意图Figure 8 A schematic diagram of porosity distributionsin Liuzhuang area
5 结语
①煤层顶底板岩石物性参数可以用地震、地质、测井相结合的方法进行定量预测。通过试验区的试验所得的数据资料,由地震资料及测井资料,采用速度标定的方法,绘制平面速度分布图,全面而更精确地描述了速度参数在三维空间的变化。
②搭建了地质与物探之间的桥梁,把过去定性的问题用定量的方法去直接实现,并用于煤矿开采的实践中去。随着技术的进步,地震信息预测煤矿地质问题将更加具有可操作性。
③由地震信息解决了岩石力学参数,为煤田开采,降低决策风险和开采施工提供了科学依据。
④目前该方法对预测岩石物性参数还有一定的局限性,如何更加有效地解决地震信息和地质信息之间的关系,还需进一步研究。

