供应链视角下林下经济产品质量安全预警模型研究

王艳萍，冯正强

（1.中南大学 商学院，湖南 长沙 410083；2.湖南外贸职业学院 国际商务学院，湖南 长沙 410200）

食品安全事关人民群众的身体健康和生命安全。为了确保食品安全，习近平强调，加强“从农田到餐桌”全过程食品安全工作，严防、严管、严控食品安全风险，保证广大人民群众吃得放心、安心。从农田到餐桌实际上就是指供应链的全过程，都必须严防、严管、严控食品安全风险。习近平还指出，“森林是水库、钱库、粮库”“绿水青山就是金山银山”。可见，森林不仅能为人民群众的生产生活提供优质的绿色产品，同时也是实现绿色发展、建设生态文明的重要保障。而且，为了加大生态系统保护，充分发挥“绿水青山”的经济、社会效益，十三届全国人大一次会议批准了国务院机构改革方案，成立了国家林业和草原局，促进形成山水林田湖草系统治理的大格局。但是，随着各地区大力发展林下经济，林下经济产品的质量安全问题也日益凸显。据统计数据显示，2015年我国食物中毒5 926 人，死亡121 人，其中有毒动植物和毒蘑菇引发的中毒事件与死亡人数分别占40.2%和73.6%[1]。可见，如何对林下经济产品质量安全问题进行准确预警，已成为食品安全领域亟待解决的紧迫问题，而科学的预警结果也为“绿水青山”向“金山银山”的转化提供了决策参考。

林下经济产品不同于一般的农产品，它的质量好坏直接影响到林业是否能变成产业，或者说影响到“绿水青山”能否变成“金山银山”。研究供应链视角下林下经济产品质量安全预警模型，就是要发现或预测林下经济产品的质量安全状态，及时发出预警并做出调整，从而实现“既要绿水青山，也要金山银山”。现有食品质量安全预警方面的研究主要集中在以下几个层面：一是对我国食品安全预警体系及其构建的研究。有学者注重从管理机构、制度、人才队伍、技术等方面探索完善我国食品安全的预警系统[2-3]。有学者侧重于研究区域性的水产养殖安全预警系统[4]；还有部分研究者重视从BP 神经网络模型、基于关联规则挖掘APTPPA 算法、食品安全的检测和检测数据等技术层面来构建食品安全预警体系[5-7]。二是对食品安全预警指标体系的研究。有学者设计了包括总体层、系统层、指标层、指数层4 个等级的食品安全预警指标体系[8]。有学者从供应链各环节入手设计了食品安全预警指标体系[9-10]。有学者从食材自身因素、生态环境因素、人工环节因素建立指标体系[11]。三是对欧盟、美国等国外食品安全预警体系的研究[12-14]。

目前学术界对林下经济产品质量安全方面的研究相对欠缺。有些学者对林产品质量安全做了一些定性研究，主要关注林产品质量安全的现状、问题与对策建议[15-16]。有学者基于VENSIM、三角模糊数犹豫直觉模糊集对林产品供应链问题进行了研究[17-18]。有学者强调应该充分利用大数据技术、条码技术、PDA 移动智能识别技术、Google maps API 等技术，建立林下经济产品的质量可追溯管理系统[19-20]。借鉴食品安全预警模型的相关研究，笔者认为通过构建基于供应链的林下经济产品质量安全预警模型，对提高和确保林下经济产品质量安全意义重大。尤其是在国家层面大力“完善天然林保护制度，扩大退耕还林还草”要求下，确保经济产品质量安全，才能让绿水青山充分发挥经济、社会效益，实现保护生态环境、提供优质生态产品、增加生态福祉的统一。

1 数据和方法

1.1 数 据

本研究中林下经济产品质量安全预警模型的应用所使用的数据是P 市历年食品安全方面的统计数据。P 市地处中国西南部，区域内生态环境良好，林下经济产品资源丰富。因此，用P 市的数据来检验基于供应链的林下经济产品质量安全预警模型具有代表性。本研究主要是通过对P 市2010—2016年林下经济产品质量安全进行评价，检验预警模型的有效性，并利用该模型对2017年P 市林下经济产品质量安全状态和发展趋势进行预警分析。研究中所用到的数据主要来源于三个方面：一是P 市2011—2018年的统计年鉴[21]；二是P 市2010—2018年食品药品监督管理局食品安全监督抽检信息公告[22]；三是2010—2018年市政府发布的食品药品和工商质监管理局食品安全监督抽检信息公告及食品安全通报[23]。

1.2 方 法

本研究主要运用可拓分析方法来建立林下经济产品质量安全预警模型。可拓分析作为一种动态综合分析模型方法，在食品安全问题研究中已有应用。该方法是我国数学家蔡文教授创立的多元数据量化决策的一种新方法，用以帮助人们遵照一定的程序找到解决问题的策略。可拓学理论认为，要研究世界，就要从研究物、事和关系的各个侧面开始，通过对它们的分析，使我们可以描述各种事物，进而描述各种矛盾。通过建立以物元、事元、关系元为基本单元的形式化描述体系，可拓理论形成了表达信息、知识和问题等的模型，称为可拓模型[24]。

定义1.2.1 把物N，特征c及N关于c的量值v构成的有序三元组R=（N，c，v）作为描述物的基本单元，称为一维物元；N、c、v则是物元R的三个要素，其中c和v组成的二元组M=（c，v），称为物N的特征元。

定义1.2.2 物N，n个特征c1，c2，…，cn及N关于ci（i=1，2，…，n）对应的量值vi（i=1，2，…，n）组成的阵列

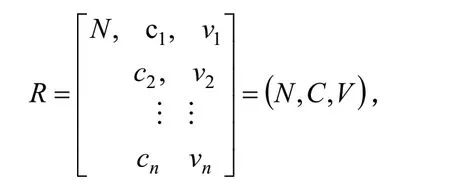
这时，称R为n维物元。

定义1.2.3 物是随时间t变化的，为此，引入参变量物元。在物元R=（N，c，v）中，如果N和v是参数t的函数，那么R就是参变量物元，记作R(t)=[N(t)，c，v]，其中v(t)=c[N(t)]。对于多个特征，则有多维参变量物元，记作：

2 建立质量安全预警模型

对食品安全预警问题的研究，理论界更多的是关注于从制度、技术层面来构建食品安全预警体系，基于供应链来研究食品安全预警模型的非常少。而且，一般人们对食品安全问题讨论多集中于生产环节，实际情况则是生产环节仅是食品供应链的一个部分。对林下经济产品质量安全预警问题的讨论应突破这种研究定式，将林下经济产品的供应、采集、加工、包装、运输、储存、销售、消费等供应链的各环节都考虑进来。林下经济产品质量安全预警是对食材质量安全问题的事前预防，其目的在于对食材供应链安全的每个环节进行预警管理，分析警像，找到警源，发现警情，并预报警度。林下经济产品质量安全预警分析的重点就是要建立预警指标体系。

2.1 林下经济产品质量安全预警指标体系的确定

从供应链的视角出发，结合文献[4-7]以及文献[8-11，17-18]，将林下经济产品的供应链划分为产地、生产、流通、储存、销售和消费等6 个环节。林下经济产品质量安全预警指标设计为3 个层次：总体指标、一级指标、二级指标。总体指标是用来反映林下经济产品供应链质量安全的总体警度；一级指标是从供应链的产地、生产、流通、储存、销售和消费6 个环节设置指标；二级指标则是由表述供应链环节的具体指标构成。基于供应链的林下经济产品质量安全预警指标体系如表1所示。

表1 基于供应链的林下经济产品质量安全预警指标体系Table1 Quality safety warning index system of forest understory economic products based on supply chain

2.2 林下经济产品质量安全预警模型的构建

2.2.1 林下经济产品质量安全的经典域、节域与预警对象

在构建林下经济产品质量安全预警模型时，将运用可拓学的理论逻辑。假设有m个林下经济产品安全等级N1，N2，N3，…，Nm，依据可拓学的逻辑便可以建立相应的物元：

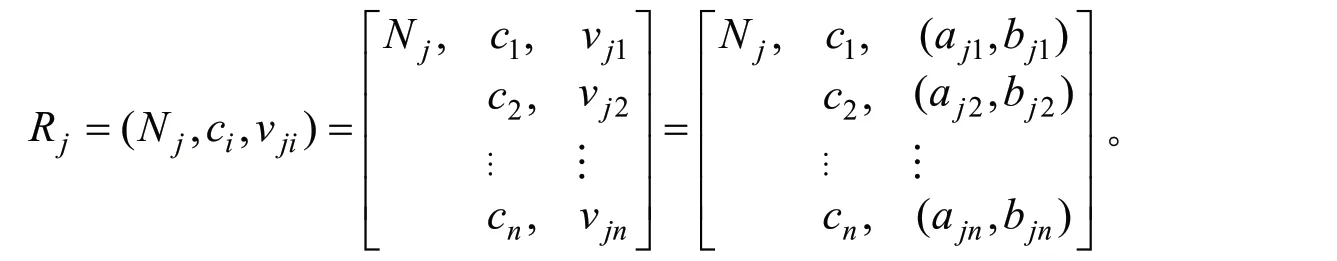
在上述物元中，Nj表示所划分的j个林下经济产品质量安全等级（j=1，2，…，m），ci（i=1，2，…，n）则表示的是质量安全等级Nj的特征，物元中vji代表的是Nj，规定ci的量值范围，也就是各个安全等级对应特征的取值范围，而Rj就是林下经济产品质量安全的经典域。对于经典域Rj，在构造节域Rp（Rp⊃Rj），可将Rp记为：

式中：Np是林下经济产品质量安全等级的全体；vip表示的是Np关于ci的量值范围。同时，对于林下经济产品质量安全的预警对象，可将预警指标信息用物元Ro来表示（如下）。在这一物元中，Po用来表示预警对象的名称，而Po关于ci的量值就是vi。

2.2.2 各安全等级关联度计算和距的确定

对于待预警对象关于各个安全等级的关联度，将用关联函数来进行计算，记为Kj(vi)，即第i（i=1，2，…，n）个指标数值域属于第j（j=1，2，…，m）个安全等级的关联函数。Kj(vi)可以表征待预警对象各项指标关于安全评价等级j的归属程度，其取值范围涵盖整个实数轴。如果存在Kj(vi)=maxKj(vi)，j∈（1，2，…，m），那么预警指标vi就属于等级j。

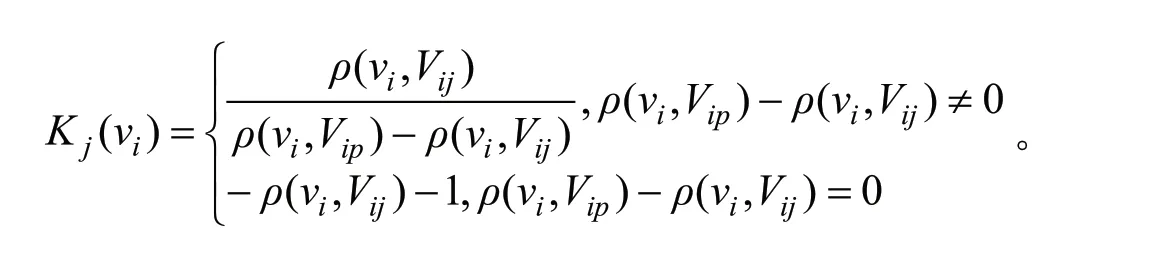
在上述关联函数中，Kj(vi)表示的就是各个安全因子关于安全级别的关联度；vi表示的是评价因子的实际数值；ρ(vi，Vip)表示的是点vi和有限区间Vip=(aip，bip)的距；ρ(vi，Vij)则表示的是点vi和有限区间Vij=(aij，bij)的距。其中，经典域为Vij= (aij，bij)，节域为Vip=(aip，bip)；而距的计算公式为：

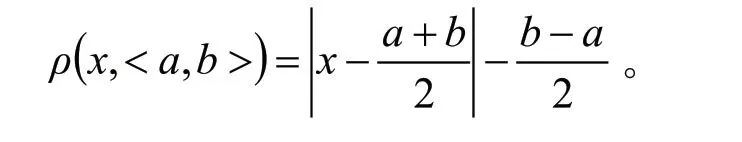
2.2.3 林下经济产品质量安全预警指标权系数

在此，我们仍采用关联函数的方法来确定林下经济产品质量安全预警指标权系数，记为：

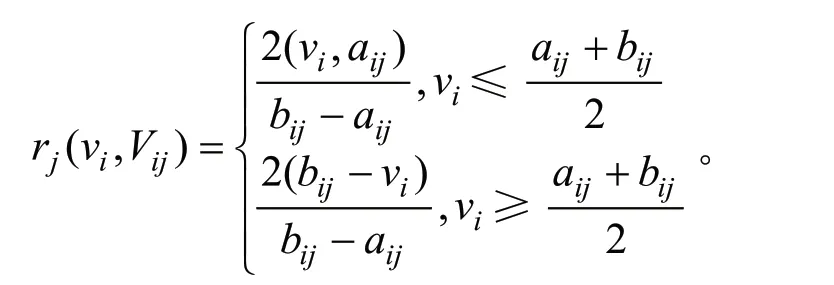
在上述函数式中，如果（i=1，2，…，m；j=1，2，…，m）且vi∈Vip（节域）（i=1，2，…，n），那么而倘若指标ci的数据落入的类别较大，则表示该指标应该赋予较大的权系数，这时的ri记为：

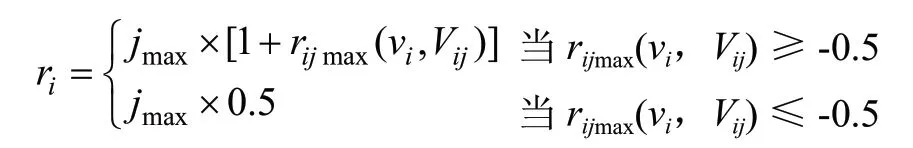
如若不然，评价指标ci的数据落入的类别较大，则表示该指标应该赋予较大的权系数，这时的ri记为：

因此，经由单个的样本数据获得的评价指标ci的权系数为：而如果再依据第k个被调查的样本数据获得评价指标ci的权系数aik(k=1，2，…，n)，通过n个样本数据权系数平均值则可以求得ci的平均权系数

2.2.4 林下经济产品质量安全等级的评定

在确定了安全等级关联度和安全预警指标权系数之后，可用K(x)的值来表示待预警对象符合食材质量安全等级的隶属程度。预警对象R0对于安全等级j的关联度可用Kj(R0)来表示，记为：

在这一条件下，倘若Kj(R0)≤1，认为，待预警对象既不符合质量安全等级的标准，又不拥有转化为该安全等级的条件，而且Kj(R0)的值越小，说明待预警对象离某质量安全等级标准的差距就越大；倘若-1 ≤Kj(R0)≤0，就认为，待预警对象也不符合质量安全等级的标准，但可以向该安全等级转变，而且Kj(R0)的值越接近0，说明预警对象的质量安全等级越容易向标准转变；倘若Kj(R0)＞0，则认为，待预警对象符合某个质量安全等级标准，而且Kj(R0)的值越大，说明符合标准的程度越高。

3 P市林下经济产品质量安全预警的应用

3.1 林下经济产品安全等级与警限

为了更加具体生动地反映林下经济产品安全度，还需要对林下经济产品的质量安全度进行安全等级标准划分。根据李克特量表理论，将林下经济产品质量安全的等级分成5 个等级：Ⅰ（红色预警），即林下经济产品存在严重质量问题，抽检不合格率特别高，引发多人食物中毒致死，或导致多人严重食源性疾病，安全级别为“非常不安全”；Ⅱ（橙色预警），即林下经济产品存在较多质量问题，抽检不合格率较高，偶尔引发轻微食物中毒或轻微食源性疾病，安全级别为“不安全”；Ⅲ（黄色预警），即林下经济产品加工、流通等环节抽检偶尔不合格，未出现食物中毒或引发食源性疾病，安全级别为“较不安全”；Ⅳ（蓝色无警），食材产地环境良好，卫生、质量抽检合格率高，安全级别为“安全”；Ⅴ（绿色安全），产地环境优质，抽检全部合格，属于纯天然绿色食品，安全级别为“非常安全”。同时，根据国家、行业以及地方食品质量安全标准，并结合现有研究文献[8-11]，确定将林下经济产品质量安全预警指标的阈值，结果见表2。

3.2 P 市林下经济产品质量安全指标权重计算与评价

根据收集的P市相关数据，运用权系数的公式，可以计算得到P 市林下经济产品质量安全预警指标权重系数，具体结果见表3。

表2 林下经济产品质量安全预警指标警限Table2 Warning limits of quality safety warning indicators for forest under-story economic products

表3 P市林下经济产品质量安全预警指标权Table3 Weight coefficients of quality safety warning indicators for forest under-story economic products in P City

通过运用ri的计算公式，可以求得P 市2010—2016年预警指标对不同安全级别的安全关联度；通过运用Kj(R0)的计算公式，可以求得各年不同安全等级的综合安全关联度；再运用就可以得到质量安全预警级别，结果如表4所示。

表4 2010—2016年P市林下经济产品质量安全预警综合评价结果Table4 Comprehensive evaluation results of quality safety warning of forest under-story economic products in P city in 2010-2016

由林下经济产品质量安全预警模型计算数据不难发现，2010—2016年P 市林下经济产品质量安全状态总体良好，2010年、2012年、2015年、2016年呈现出非常安全的状态，预警状态为“绿色安全”；KIV(R2011)=0.162 03、KIV(R2013)=0.561 43，说明这两年P 市林下经济产品质量为“安全”，预警状态则是“蓝色无警”；而且，KV(R2011)=-0.227 59、KV(R2013)=-0.155 66，说明2011年和2013年P 市林下经济产品质量安全状态有向“非常安全”转化的良好态势。

KIII(R2014)=0.156 00，说明2014年P 市林下经济产品质量为“较不安全”，预警状态为“黄色预警”；KIV(R2014)=-0.038 71，说明2014年P 市林下经济产品质量安全状态有向“安全”转化的趋势。这些数据结果与P 市食品质量安全的实际情况是基本一致的，特别是2014年P 市出现了由林下经济产品引发的11 例食物中毒、3 例食源性疾病。这进一步说明，运用可拓学理论建立的林下经济产品质量安全预警模型是有效的、合理的。

将2017年P 市林下经济产品质量安全预警指标值代入预警模型，可得到2017年P 市林下经济产品质量安全评价结果，结果见表5。由表5可见，在指标体系中，符合“非常不安全”、“不安全”的指标值没有。除了KIV(C4)=0.327 59、KIV(C5)= 0.171 46、KIV(C7)=0.368 42、KIV(C13)=0.204 84、KIV(C14)=0.342 86、KIV(C16)=0.433 60， 即2017年P 市林下经济产品卫生抽检合格指数、农药残留抽检合格指数、林下产品包装合格指数、林下产品理化指标检测合格指数、林下经济产品食用中毒人数、食源性疾病引发次数处在“安全”的状态。其余指标都处在“非常安全”的水平，尤其是水环境、空气环境、土壤环境指标处在“非常安全”状态，确证了P 市生态环境优良的事实。从变化趋势来看，KV(C4)=-0.0193 52、KV(C5)= -0.322 22、KV(C7)=0.661 21、KV(C14)=-0.490 79、KV(C16)=-0.064 44，这些指标有向“非常安全”状态转化的趋势。但是，KV(C13)=-0.307 11，说明林下产品理化指标检测合格指数有向“较不安全”转化的趋势。从2017年的数据来看，P 市林下经济产品质量安全的隐患可能主要来自于销售环节的理化因素。总体来看，KIV(R2014)=0.089 30，即2017年P 市林下经济产品质量安全为“蓝色无警”，KIV(R2017)=-0.515 03，说明总体质量有向“绿色安全”状态发展的趋势。

4 结 论

从供应链的角度来构建林下经济产品质量安全预警模型，并将该模型建立在可拓学的理论基础之上，用定量评价的方式提高了林下经济产品质量安全预警能力，可以为食品安全监管与预警提供指导。

1）本文通过建立林下经济产品质量安全预警模型，对P 市林下经济产品质量安全进行评价，计算得到其林下经济产品总体安全的结论。而且，从2014年的食物中毒、食源性疾病来看，病因是偶发性的。因此，P 市林下经济产品质量安全的级别较高，绝大多数年份都处在“安全”或“蓝色无警”水平之上，数据结果与实际情况也基本一致。

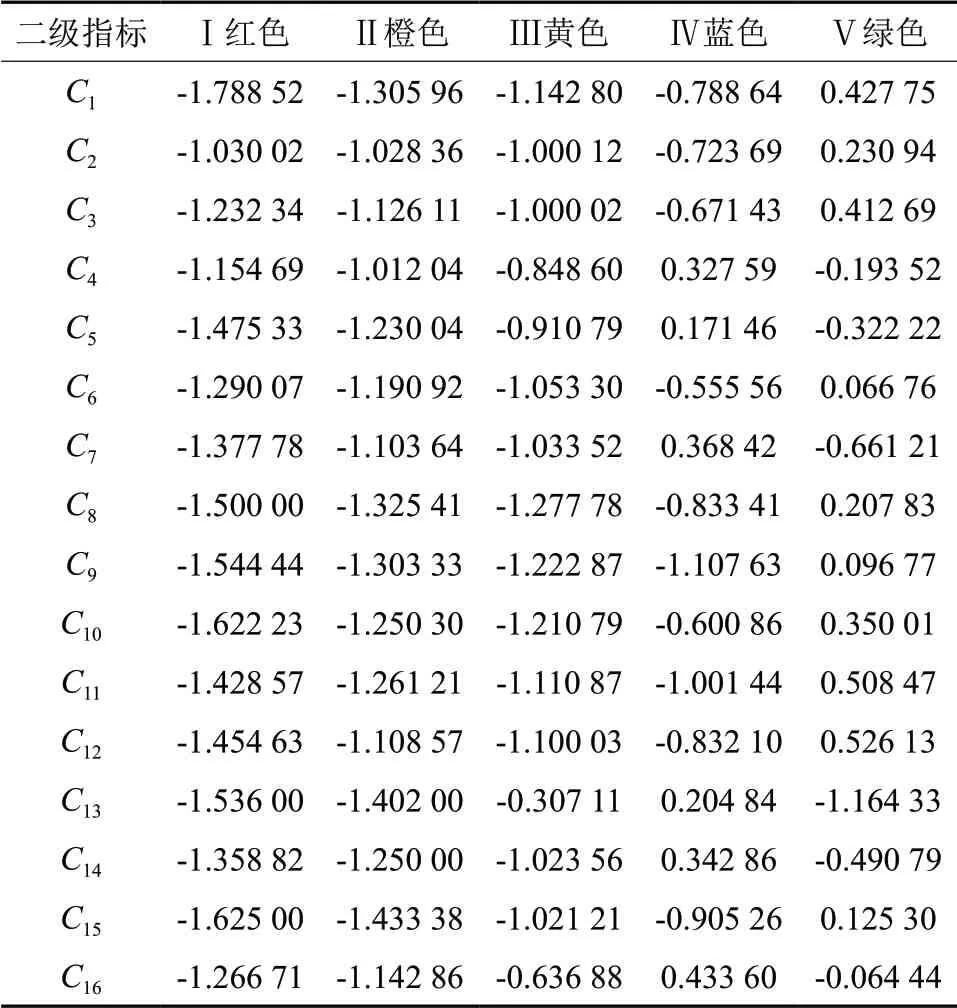
表5 P市2017年林下经济产品质量安全评价结果Table5 Evaluation results of quality safety of forest under- story economic products in P city in 2017

2）该模型基于供应链的视角，将林下经济产品从产地环境、加工、流通、储存、销售、消费等环节全部纳入评价体系，将供应链的整个流程和要素都予以考评，提高了预警模型的针对性、科学性与有效性。涉及林下经济产品质量安全的最关键环节就是生产环节，影响因素主要是食材自身因素和生态环境因素。安全预警指标体系设计需要考虑环境因素，安全监管也需要将环境因素纳入考虑范围。有研究者便认为，保障食品安全就可以从环境规制着手：一方面要完善我国相关的环境法体系，另一方面需要在食品安全法中加强对环境的要求，强化环保部门职责，建立食品安全全程环境监控制度[25]。同时，可拓学的理论又为该区域林下经济产品质量安全进行了综合评价，明确了安全等级和警情等级，可以为该区域的食品安全监管部门的监管和预警提供科学的决策数据。

3）预警模型的依据是量化的数据指标，可得到客观的安全等级和预警等级的结论数据。而且，还可以通过Kj(R0)的取值区间，得到林下经济产品安全等级和预警等级的变化方向，赋予了指标数据的动态性特点。这也为该区域的食品安全工作特别是食品安全监管部门的下一步工作指明了方向。尽管本研究不能对每一种食材或每一种风险确立监测指标，但是可以通过公众的广泛参与，促进政府部门与公众的良好的风险交流，培育参与式的监管治理格局，形成风险界定的有效社会监督[26]。林下经济产品质量安全既需要量化的数据指标进行预警，也需要公众和监管部门对生产环境和供应链环节进行有效监督。

4）用可拓学理论构建的预警模型在可扩充性和灵活性上更强。该预警模型既可以对林下经济产品的单个影响因素进行单指标安全预警分析，又可以将整个指标体系化整为单指标，确定整个区域对象或该区域一定时间段的质量安全状态，并进行有效预警，使模型的可扩充性和灵活性大大提高。同时，借助该模型得出的预警结论更客观、更准确。基于可拓学理论构建的预警模型克服了专家预警、指数预警、模拟预警对多因素、多尺度和多时段预警问题时的主观性和片面性。根据相关质量安全数据，不仅能定量评价林下经济产品安全预警状态，还能对该产品安全状态的发展趋势进行预测，且具有一定的准确性，2017年P市林下经济产品安全预警实例分析证实了这一点。