M olecule opacitiesof X2Σ+,A2Π,and B2Σ+statesof CS+*

Xiao-He Lin(林晓贺),Gui-Ying Liang(梁桂颖),Jian-GuoWang(王建国),Yi-Geng Peng(彭裔耕),Bin Shao(邵彬),Rui Li(李瑞),3,‡,and YongWu(吴勇),4,§

1SchoolofPhysics,Beijing Institute ofTechnology,Beijing 100081,China

2Institute ofApplied Physicsand ComputationalMathematics,Beijing 100088,China

3DepartmentofPhysics,College ofScience,QiqiharUniversity,Qiqihar161006,China

4HEDPS,CenterforApplied Physicsand Technology,Peking University,Beijing 100084,China

(Received 29 January 2019;revisedmanuscript received 28 February 2019;published online4 April2019)

Keywords:CS+,dipolemoment,transition dipolemoment,opacity

1.Introduction

Carbon sulf idecation(CS+)has received considerableattention ow ing to its dom inant role in spectroscopy and astrophysics.In astrophysics,several sulfur compounds[1–6](CS,CS+,HCS+,C2S,C3S,and C5S)have been observed in interstellarmolecular clouds,and the CS+molecular ion is the f irstsulphur-bearingmolecular detected in diffuse interstellar clouds.[6]Because CS+isashort-lived and highly reactivediatom icmolecular ion,the CS+ion isusually considered asan important precursor and an intermediate in the formation of HCS+.[7,11]The protonatedmolecular ion HCS+[2]has been detected in the interstellarmedium through radio-astronomical spectra,and hasattracted extensiveattention to understand the sulfur chem istry of interstellar clouds.In spectroscopy,preciseand reliable spectroscopic constantsand vibrationalproperties ofmoleculesare effective in investigating properties of diatomicmolecules.Themolecular constants of CS+can be used asa diagnostic of the CS+abundancy in outer space.

On the theoretical side,a number of previous studies have aimed to understand the low-lying electronic states of CS+ion.In 1985,Larsson[8]used the complete active space self-consistent f ield(CASSCF)and conf iguration interaction methods to calculate potentialenergy curves(PECs)and spectroscopic constants for the X2Σ+,A2Π,and B2Σ+states of CS+.Based on the CASSCFwave functions,he also obtained the electronic transitionmoments for the A2Π–X2Σ+,B2Σ+–X2Σ+,and B2Σ+–A2Πtransitions,and evaluated the radiative lifetimesof the A2Πand B2Σ+states.In 2008,Honjou[9]studied the potential energies of the X2Σ+,A2Π,B2Σ+,and C2Σ+states of CS+by employing the ab initio method and simulated the photoelectron spectrum of CS.In 2010,Chenel etal.[10]studied the adiabatic potentials and couplings of the2,4Σand2,4Πstates in theCS+system employing themultireference conf iguration interaction(MRCI)method and obtained the charge transfer crosssectionsusing thequantum and sem iclassical approaches.Later,the vibrational levels for X2Σ+and A2Πstatesof CS+were determ ined byWang etal.[7]and Kaur etal.[11]atMRCI level of theory.In 2013,Li etal.[12]used theMRCImethod with Davison size-extensivity correction(+Q)to calculate the potential energy curves of the lowlying 18Λ–Selectronic statesof CS+correlatingwith the two lowestdissociation lim its.

On the experimental side,Coxon[13]measured the intensity and wavelength for the CS+(A2Π–X2Σ+)band system excited by the reaction of metastable He with CS2.Latter,Tsuji et al.[14]and Cossart et al.[15]measured and analyzed the CS+(B2Σ+–X2Σ+)emission spectrum in the220–340 nm region.In 2002,Liu etal.[16]studied theabsorption spectrum of the(5,0)and(6,0)bandsof the X2Σ+→A2Πtransition of CS+employing velocitymodulation absorption spectroscopy.Recently,Li etal.[17]measured theabsorption spectrum of the(2,1)band in the A2Π–X2Σ+system of CS+by using the opticalheterodyne velocitymodulation absorption spectroscopy.

A lthough CS+ion has great signif icance in astrophysical environments,the accurate and systematic study of the absorbed cross sections is lim ited and scarce.The previous studies of CS+aremainly lim ited on the basic spectroscopic constantsandmolecular structure calculations.In the present work,the PECs and transition dipolemoments(TDMs)are computed by employing the ab initio method.Based on the calculatedmolecularstructuredata,thevibrationalenergy levels,vibrationalwave functions,and spectroscopic parameters of bound states of CS+are obtained by solving the nuclear Schr¨odinger equations.Finally,the rovibrational transition lines of the considered states of CS+are calculated for different temperaturesand pressure conditions.

This article is organized as follows.In Section 2,we brief ly outline the computationalmethods for the calculations of PECs,TDMs,vibrational energy levels,and opacity.In Section 3,we discuss our results for the spectroscopic properties of the X2Σ+,A2Π,and X2Σ+states,the corresponding vibrationalenergy levels,TDMs,and opacity.Finally,a brief summary isgiven in Section 4.

2.Theoreticalmethod

In thiswork,electronic statesof CS+are calculatedwith Molpro 2010[21]suite of quantum chem ical procedure.The pointgroup of CS+is C∞v,and all the calculations are done in the C2vsubgroup.The electronic states of CS+are described by irreducible representations of C2v,and the corresponding relationship between the electronic states and irreducible representations of C2vareΣ+=A1,Σ-=A2,Π=B1+B2,andΔ=A1+A2.For the basis sets adopted in the calculations,the contracted Gaussian-type basis sets aug-ccpwCV5Z-DK[22–24]are chosen for C and S atoms,respectively.To obtain the precise PECs of the low-lying states of CS+,singlepointenergiesata seriesof internucleardistances are computed.The calculated process of single pointenergy includes the follow ing threesteps.First,themolecularorbitals(MOs)of X2Σ+are computed with the Hartree–Fock(HF)self-consistent f ield method.Then,the 3 lowestΛ–S states of CS+are calculated by the state-averaged complete active space self-consistent f ield(SA-CASSCF)[25,26]using HFMOs as the starting orbitals.Finally,utilizing the reference wave functions obtained from the SA-CASSCF calculation,the internally contracted MRCImethod is adopted to compute the single pointenergy of the electronic state.In the above SACASSCF calculation,the selection of active space is very important for the precision of single pointenergy.Hence,differentactive spaceshavebeen tested,and f inally eightoutermost MOs(four A1,two B1,and two B2)are selected as the active space,corresponding to 2s2p(C)and 3s3p(S)atomic orbitals.In theMRCIcalculation,a totalof10 electrons(2s22p2electrons of C and 3s23p4electrons of S)of CS+are taken into account in the computation of electronic correlation energy.The Davison size-extensivity correction[27–29](+Q)is also included in theMRCIcalculation to balance the the sizeconsistency error.The scalar relativistic effect is computed with third-order Douglas-Kroll[30]and Hess[31]integrals.

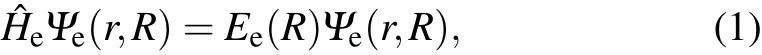
Under the Born–Oppenheimer approximation,the electronic Schr¨odinger equation of diatom ic molecules can be w ritten as inwhichΨe(r,R)and Ee(R)are the eigen-function and eigenenergy,respectively.ˆHeis the Hamiltonian for the N electrons diatom icmoleculesgiven by where Zaand Zbare the charge numbersof nucleiA and B.

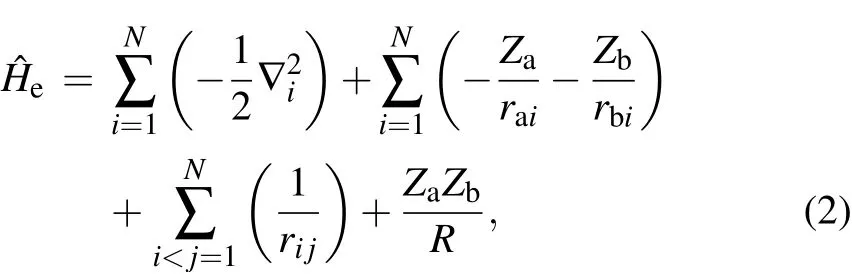
On the basis of calculated energies of electronic states,theeigenvaluesandwave functionsofvibration-rotation states can be obtained by solving the follow ing radical nuclear Schr¨odingerequation utilizing LEVEL program:[32]where EνJ(R)is the vibration-rotation level.

The Einstein coeff icient between two vibration-rotation levels isdef ined as

whereαis the f ine-structure constant,ων′j′,ν′′j′′is the transition frequency of two vibration-rotation levels,and line strength(SJ′J′′)and H¨onl–London factor[33](φJ′,J′′)are determined by

Totalinternalpartition function Q(T)issummed over the concerned electronic stateweighed by theBoltzmann factorutilizing in which Tiis the excitation energy of electronic state i,and T is the environment temperature.Qei=(2S+1)(2-δΛ,0),where S is the electronic spin quantum number,2S+1 is the multiplicity,Λis the electronic orbital quantum number:0,1,2,3,...forΣ,Π,Δ,Φ,...electronic states,respectively,andδis the Kronecker delta.Qvi×Qriis the summation over all possible rovibrational de-excitation transitions within the electronic state i,and Qvi×Qri=(2J′′+1)∑ν′′J′′e-ΔEν′′J′′,00/kT,whereΔEν′′J′′,00is the excitation energy of state(i,ν′′,J′′)and 0 for theground state.

The integrated line strength is the molecular opacity,[34–36]which isgiven by

where E′′is theexcitation energy of the lowerelectronic state in unitsof cm-1,ΔEν′J′,00is rovibrationalexcitation energy of energy levelν′,J′,Q(T)is the total internalpartition function,and the Einstein A-values for each line are computed using formula(4).

3.Resultsand discussion

3.1.Potential energy curves,spectroscopic constants,and vibrational levels

Asplotted in Fig.1,three electron states,namely,X2Σ+,A2Π,and B2Σ+,are computed.A llof the states thatare correlated to the two lowestdissociation lim itsC(3P)+S+(4S)and C+(2P)+S(3P)of CS+are typically bound and calculated with theMRCI+Qmethod utilizing the aug-cc-pwCV5Z-DK basisset.

On the basis of the calculated PECs,the spectroscopic constantsareobtainedwith thenumericalmethod and listed in Table 1,including adiabatic transition energies Te,harmonic vibrational frequenciesωe,anharmonic termsωeχe,rotational constants Be,and equilibrium distances Re.To verify the accuracy of our calculation,Table 1 also gives the available theoretical results and experimental values.For the ground state X2Σ+,the Beand Reare in good agreementwith theexperimental results,and the deviations are 0.002046 cm-1and

Fig.1.Calculated potential energy curves for the X2Σ+,A2Π,and B2Σ+statesof CS+.

Tab le1.Computed and experimentalspectroscopic constantsof CS+.

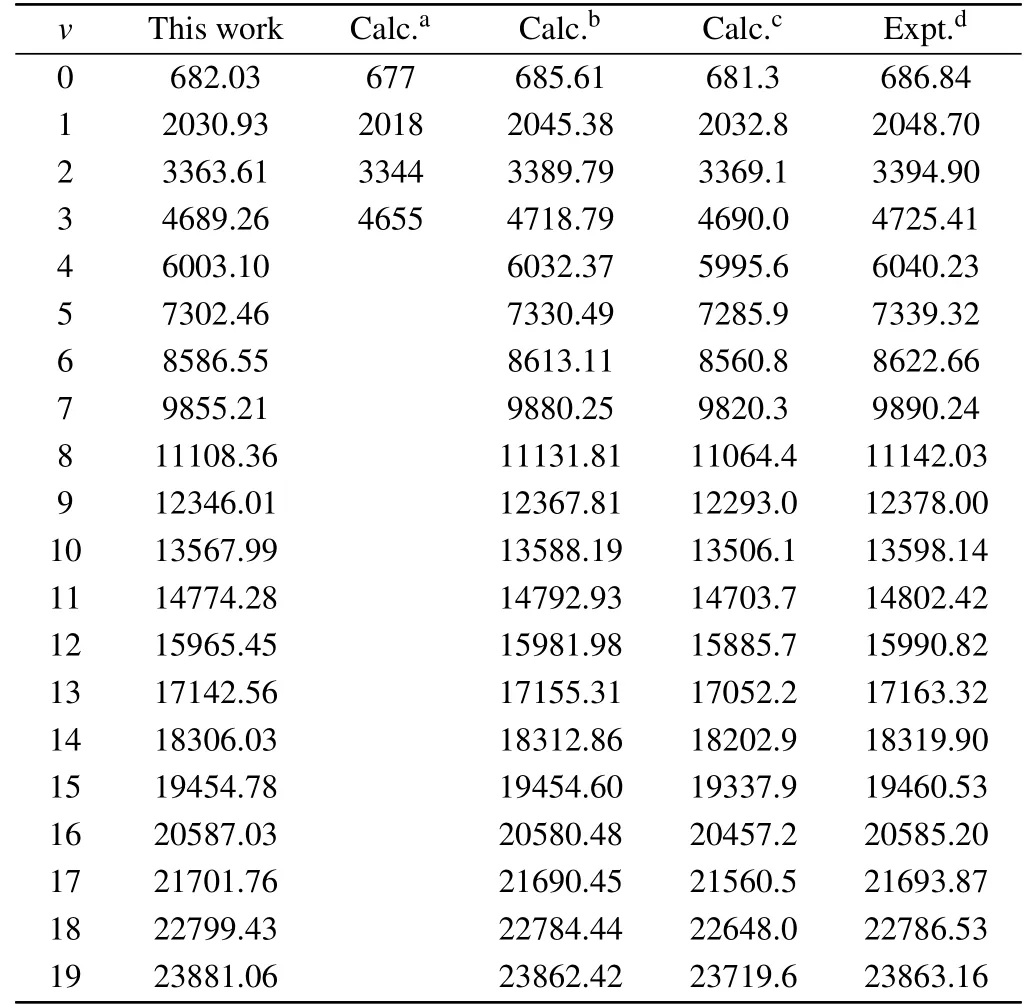
Table 2.Calculated vibrational levels Ev for the X2Σ+states of CS+(in cm-1).

Table3.Calculated vibrational levels Ev for the A2Πstatesof CS+(in cm-1).

and 0.002444˚A,respectively.For the low lying excited state A2Π,the calculated transition energy Teis11709 cm-1,while the recent experimental result is 11987.25 cm-1,the deviation is only 278.25 cm-1.Equilibrium distance Revalue is in accord with the results of experiment,with the error of 0.00105˚A.For the second excited state B2Σ+,the adiabatic excitation energy is 36869 cm-1,as shown in Table 1.Moreover,theverticalexcitation energy of B2Σ+is40271 cm-1and the energy gap between B2Σ+and A2Σ+is 8122 cm-1at the asymptotic region.The harmonic vibrational frequenciesωeand anharmonic termsωeχe,which are determined by the vibrational terms,are suitably consistentwith the experimental results,within themaximum differences of 18.18 cm-1and 2.1552 cm-1,respectively.The differences of Teand Reare 0.9%and 0.6%between our results and experimental values,respectively.

To conf irm theaccuracy ofourcalculation,thevibrational levels of the X2Σ+,A2Π,and B2Σ+states are also given.In Tables 2–4,our calculated results are close to both of the experimental results and the existing theoretical values.For the ground state X2Σ+,our computed vibrational levels are up toν=19,the results are in accord with the measurement results.[16]For the A2Πstate,themaximum deviation is2.225%in comparingwith the experimental data.[16]In addition,our calculated energy level of the B2Σ+state is close to the previously available theoretical result.[9]A ll the spectroscopy constants and vibrational levels can provide importantparameters for the calculation of the spectrum.

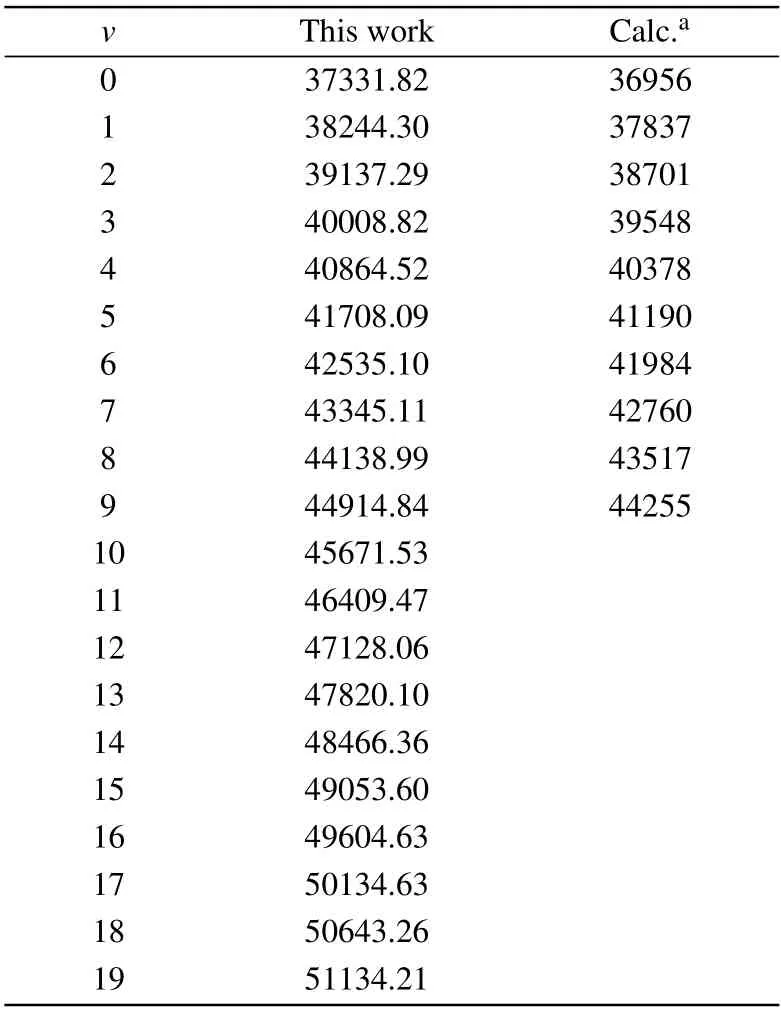
Table 4.Calculated vibrational levels Ev for the B2Σ+states of CS+(in cm-1).

3.2.Electronic transition dipole moments and radiative lifetimes

The dipole moment(DM)and TDM s of the low-lying statesare calculated by utilizing MRCImethods.TheDM and TDM curves are presented in Fig.2.As shown in Fig.2,the DM for the X2Σ+state changeswith the increasing bond,and the calculated DM of the state tends to be a negative value because of the dissociation lim its C(3P)+S+(4S)of the CS+ion.The TDM s from the X2Σ+state to theexcited states A2Π and B2Σ+are calculated as a function of the internuclear distance,also depicted in Fig.2.The TDM of X2Σ+–B2Σ+is much larger than that of X2Σ+–A2Πas displayed in Fig.2.

Themaximum TDM of X2Σ+–B2Σ+is located at thedistance of R=5.48 a.u.

The Frank–Condon factorsof the X2Σ+–A2Πand X2Σ+–B2Σ+systems,which are calculated with the aid of the LEVEL program,are listed in Table 5.The computed values,whose change trends are irregular,are in good agreement with the previous experimental results.As shown in Table 5,the Frank–Condon factor of the 0–0 band is 0.0265 for X2Σ+–A2Π,which is close to the experimental value of 0.0355.While the Frank–Condon factors for the X2Σ+–B2Σ+system arealso obtained for the f irst time.

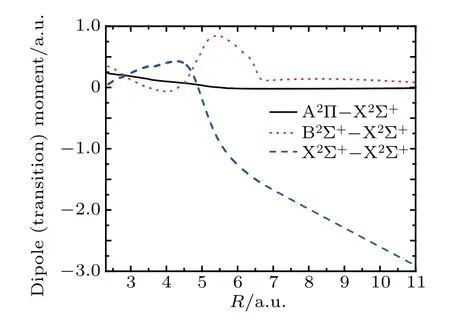
Fig.2.Transition dipolemoments fordifferentstatesof CS+asa function of internuclear distance R.

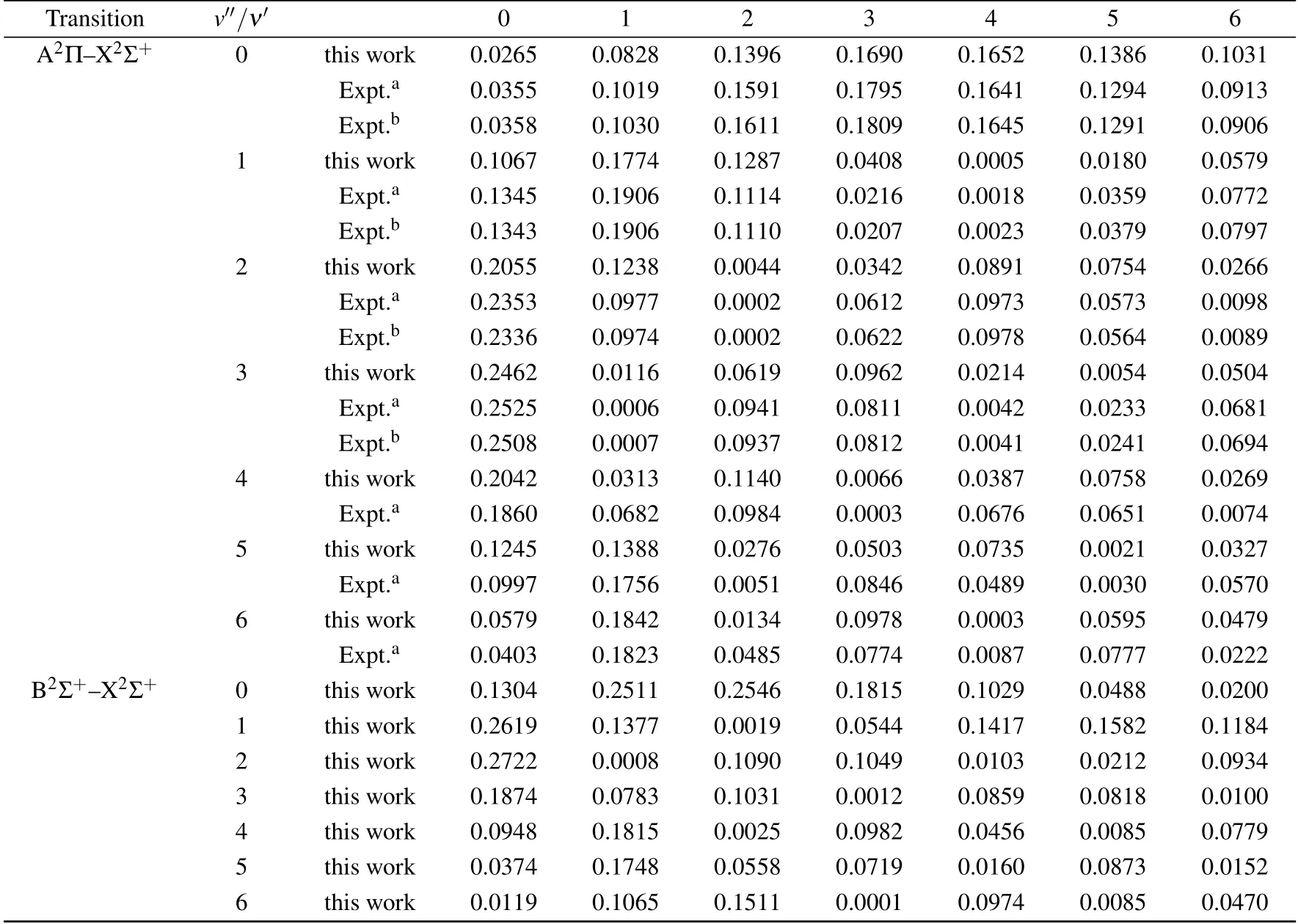
Table5.Franck–Condon factors for the A2Π–X2Σ+and B2Σ+–X2Σ+transitionsof CS+.

On basisof this transitions information,the radiative lifetimesof thecorresponding vibrational levelsareobtained.The radiative lifetimes are determ ined by the summation of the Einstein coeff icients Aν′ν′′

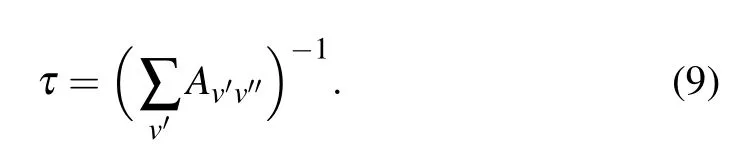
The Einstein coeff icient,which isaparameter forspontaneous emission between vibrational levelsν′andν′′,isdef ined as whereΔEν′ν′′is theenergy gap of thevibrational levelsν′and ν′′in unitsof cm-1,TDM is theaverage transition dipolemoment in the atom ic unit,while the last term(∫ψv′ψv′′d r)2is the Frank–Condon factors for thevibrational levelsν′andν′′,and the radiative lifetime is in unitsof second.

The concrete calculation results for the selected vibrational levels for transitionsof A2Πand B2Σ+are tabulated in Table6.The longest radiative lifetimeof A2Πis32.90μsowing to the small transition dipolemomentsof the X2Σ+–A2Π transition.

Table 6.Radiative lifetimes of several electronic states at low-lying vibrational levelsof CS+(inμs).

3.3.Opacity

The partition function and opacity of CS+are computed on the basis of the results of vibrational level,wavefunction,DM,and TDM.For the partition function,which isan importantparameter in radiative transfer and spectroscopy analysis in the astrophysical f ield,is calculated with different temperatures in the range of 10–4500 K.In thiswork,the values of the partition function areobtained by summ ing allover the rovibrational states of the lowest three states,and the results of thepartition function are listed in Table7,and the corresponding f igure is rendered in Fig.3.As shown in the results,the partition functions augmentwith increase of the temperature according to formula(7).

In our calculation,the opacity is convolved by a Lorentzian line prof ilewithw idth corresponding to collisional broadening.[36–38]By utilizing a canonical collisional broadening cross section of 10-16cm2with a line w idth proportional to the pressure,f igure 4 presents the opacities of CS+at the temperatures of 300 K,500 K,1000 K,and 4500 K with the pressure of 100 atms.As shown in Figs.4(a)–4(d),the spectra aremainly lying in the range of ultraviolet to farinfrared,which include three bandsobtaining from the transitionsof the threeelectron states,namely,X2Σ+–X2Σ+,X2Σ+–A2Π,and X2Σ+–B2Σ+,from right to left.From Figs.4(a)and 4(b),it is clearly observed that each band system is different at temperatures of 300 K and 500 K.As depicted in Figs.4(a)and 4(b),the band systems corresponding to X2Σ+–A2Πand X2Σ+–B2Σ+appearat243 nm and 683 nm,respectively,which are associated with the short-wave ultraviolet range.For theband of X2Σ+–X2Σ+,the strong pure rotational lines are located in the range ofλ＞10μm.And the vibrational band ofΔν=1 appears near 7.3μm.It can be found that theopacitiesofmoleculararedistinguishableandweak in the range of 1200–3600 nm.Meanwhile,as temperature increases,the cross section grows and the systems of different bandsare fuzzy,which contribute to the enhanced population of the vibrational excited and electronic stateswith the high temperature.At the same time,the pure rotational spectra are reduced because of the decreased populations of the ground stateas the temperature increases.

Tab le7.Partition function Q for CS+asa function of temperature.

Fig.3.Partition function for CS+.

Fig.4.Opacitiesof CS+ro-vibrational transitions for temperaturesof(a)300K,(b)500K,(c)1000K,(d)4500K and apressureof 100 atms.Note that threeelectronic statesof X2Σ+,A2Π,and B2Σ+havebeen included in the presentcalculations.

4.Conclusion

In the present work,the PECs of the X2Σ+state and two excited states A2Πand X2Σ+are calculated with the MRCI+Q method.On the basis of the PECs,the corresponding spectroscopic constants and vibrational levels are obtained,which agreewellwith theexperimental results.The TDM s of the two excited states to the ground state X2Σ+are obtained,and the radiative lifetimes of A2Πand X2Σ+states are also obtained.The cross sections for the three lowest lying states are given at 300 K,500 K,1000 K,and 4500 K under the pressure of 100 atms.It is shown that the spectra are clearly separated for the temperaturesof300K and 500K both for the vibrational transition and the electron transitions.However,with the increase of the temperature,the population on the excited states cannot be ignored,and the boundaries of the lines become blurred.At the same time,the partition functionsarealso found in the rangeof10–4500K.Theaccuracy of electronic structuresand opacities ofmolecule for the low-lying three states providemore information tomodel the atmosphere calculation.