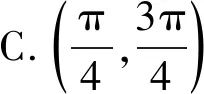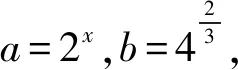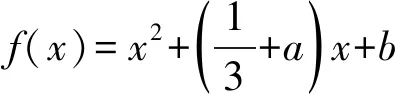“函数与导数”高考复习专题*
(北京师范大学台州附属高级中学,浙江 台州 318020)
1 知识内容
1.1 函数与导数在高考中的地位
函数是高中数学的一条主线,在历年高考中都是兵者必争之地,不但内容丰富、形式多样,而且在其他内容中也渗透考查,核心素养立意高,是评价考生核心素养的一个重要载体.导数的应用深化了对函数本质的理解.函数与导数突出考查函数与方程思想、数形结合思想、分类讨论思想以及化归思想,从而考查考生的逻辑推理能力、数学抽象能力、直观想象能力、数学运算能力以及进一步学习数学的能力.因此,函数与导数常作为压轴题的内容在近年的高考中不断推陈出新.
1.2 函数与导数的内容与方法
从知识上看,函数与导数部分主要考查:1)函数的概念;2)函数的四性(单调性、对称性、周期性和凹凸性)和两域(定义域和值域);3)初等函数的概念与性质;4)函数与方程(函数零点);5)函数与不等式;6)导数的概念、运算、应用.
函数与导数的常见题型有:1)求函数定义域、值域;2)求函数的解析式或图像;3)讨论(或利用导数)函数的四性;4)利用函数性质、图像或导数解决函数、方程(函数零点)、不等式等问题;5)(利用导数)讨论函数之间的关系.
解答函数与导数试题的常用方法有换元法、赋值法、待定系数法、图像法、变量分离法、利用概念定义、逻辑推理法.
特别是考查导数内容的试题要求高,常用方法有:1)图像法;2)变量分离法;3)利用导数的几何意义、切线斜率和瞬时变化率等概念求解(即洛比达法则和端点效应);4)利用高等数学的定理(微分中值定理、泰勒展开式等)解决等.
从函数的知识、方法上看,内容多、方法巧、立意高,特别是含多变量的函数试题,需分解为几个基本函数,研究这几个基本函数的性质,进而得到整个函数的性质.
2 典例剖析
2.1 合理分离变量,强化本质理解
例1设函数f(x)=ax2+x|x-b|,其中a,b∈R.
1)当b=-1时,若不等式f(x)≥-2x-1恒成立,则实数a的最小值为______;
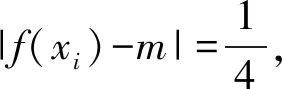
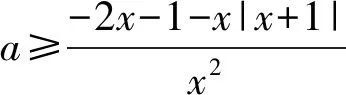
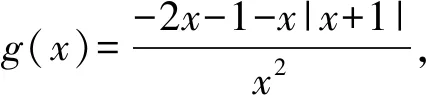
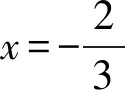
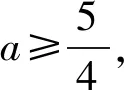
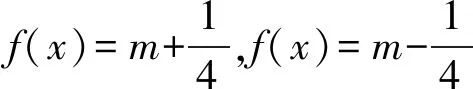
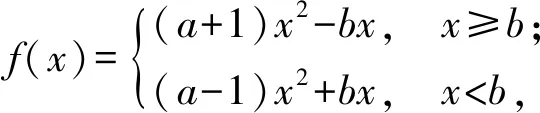
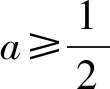
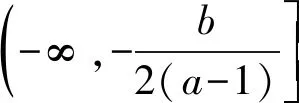
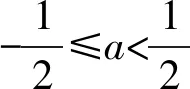
得
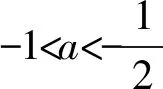
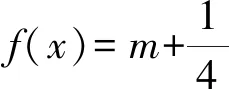
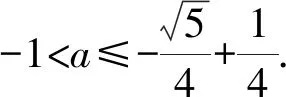
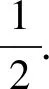
2.2 注重分类讨论,回归概念及本质
例2设函数f(x)=x2+|ax-1|,其中a∈R.求f(x)在[-1,1]上的最小值m(a).
分析1(直接分类讨论)
1)当a>0时,
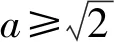
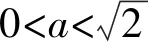
2)同理当a<0时,
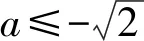
3)当a=0时,显然f(x)的最小值为1.
因此,f(x)在[-1,1]上的最小值为
分析2(转化为最值概念)由最值概念知:当x∈[-1,1]时,f(x)=x2+|ax-1|≥m(a)恒成立,即当x∈[-1,1]时,x2≥m(a)-|ax-1|恒成立.
考虑函数g(x)=x2(其中x∈[-1,1])的图像及折线h(x)=m(a)-|ax-1|的关系:

h(x)=m(a)-|ax-1|=
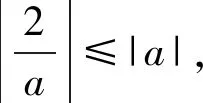
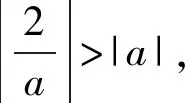
2)当a=0时,显然f(x)的最小值为1.
因此,f(x)在[-1,1]上的最小值为
评注函数中概念很多,甚至含有多个参变量.要解决此类问题,首先要理解有关概念,并学会根据产生分类原因确定分界点,并进行分类讨论;其次是深层次理解有关概念及本质并能运用它们解题.本题是典型的运用概念的问题,可运用函数的最值概念及图像之间的关系求解,减少分类讨论.
2.3 合理分离函数,强化数形结合
例3若存在实数a,b,对任意的实数x,不等式ex+ax2≥b恒成立,求a-b的最小值(其中e是自然对数的底数,e≈2.718 28…).
分析1(分拆成基本函数)原问题转化为:对任意的x,ax2-b≥-ex恒成立,求a-b的最小值.
设f(x)=-ex,g(x)=ax2-b,则
f(x)≤g(x),a-b=g(±1).
从而
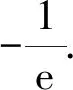
解得
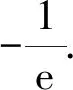
分析2(构造直线模型)原问题转化为:对任意的x,ax2-b≥-ex恒成立,求a-b的最小值.
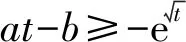
评注合理分离出基本函数,从基本函数之间的关系、运算等角度思考问题,往往对多变量的函数问题解决有很大的帮助,可以大大降低运算及思维难度,进而理解问题的本质.
2.4 构造函数,凸显函数性质
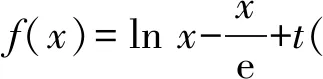
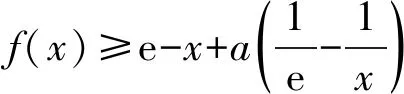
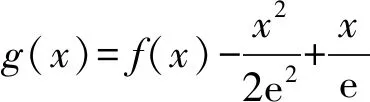
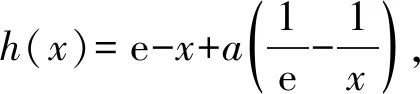
f′(e)=h′(e)=0,
因此
a=e2.
又当a=e2时,
从而当x≥e时,f′(x)≥h′(x);当x≤e时,f′(x)≤h(x)′,因此a=e2.
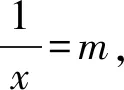
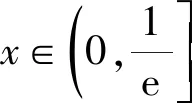
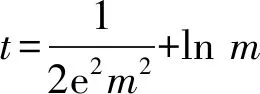
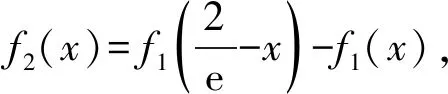
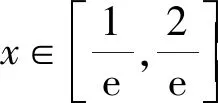

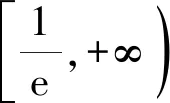
即
评注本题第1)小题是典型的端点效应问题,利用导数的几何意义和瞬时变化率的含义,得到必要条件,为证明打下坚实的基础.第2)小题是典型的极值点偏移问题,往往利用对称构造另一侧函数,利用导数讨论单调性,进而找出问题的本质,即导数变化率的变化快慢问题.
2.5 注重变化,变化中找突破口
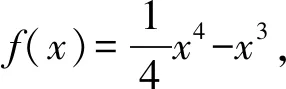
分析若分离出变量m,则对任意的实数k有且只有两个不同的实根,不好处理.若分离出变量k,则相对容易操作.
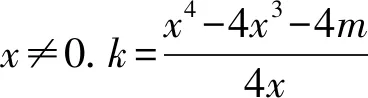
令p(x)=3x4-8x3+4m,则p′(x)=12x2(x-2),p(x)在(-∞,2)上单调递减,在(2,+∞)上单调递增,于是p(x)min=p(2)=4m-16.
1)当4m-16≥0,即m≥4时,h′(x)≥0,即h(x)在(-∞,0),(0,+∞)上单调递增,且当x→-∞时,h(x)→-∞;当x→0-时,h(x)→+∞;当x→0+时,h(x)→-∞;当x→+∞时,h(x)→+∞.此时对任意的实数k,原方程有且只有两个不同的解.
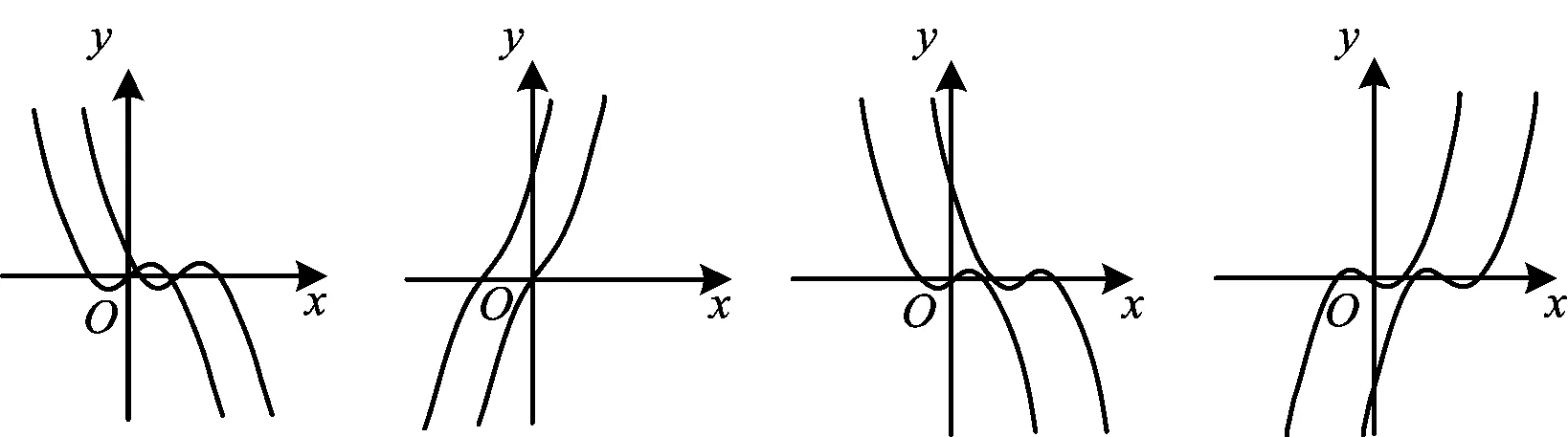
2)当0 3)当m<0时,p(x)有两个异号的零点x1,x2,不妨设x1<0 又当x→-∞时,h(x)→-∞;当x→0-时,h(x)→-∞;当x→0+时,h(x)→+∞;当x→+∞时,h(x)→+∞,从而当h(x1)=h(x2)时,对任意的实数k,原方程有且只有两个不同的解,于是 得 由h(x1)=h(x2),得 即 从而 因此 m=-1. 当m≥4或m=-1时,原方程对任意实数k均有且只有两个解. 1.已知函数f(x)=x(1+a|x|)(其中a∈R),在同一个坐标系下函数f(x+a)与f(x)的图像不可能的是 ( ) A. B. C. D. ( ) A.1 B.2 C.3 D.4 3.已知θ∈[0,π),若对任意的x∈[-1,0],不等式x2cosθ+(x+1)2sinθ+x2+x>0恒成立,则实数θ的取值范围是 ( ) 1)若函数f(x)在(0,2)上存在两个极值点,求3a+b的取值范围; 8.已知函数f(x)=e1-x+alnx有两个极值点x1,x2(其中x1 1)求实数a的取值范围; 2)求证:x1+x2>2; 3)求证:x1x2<1. 参 考 答 案 1.D 2.D 3.A 7.1)3a+b的取值范围是(-8,0). ①当b≥0时,f′(x)≥0在[0,2]上恒成立,从而f(x)在[0,2]上单调递增,于是 因此 只需证 即证 又g(1)=a-1,当x→0+时,g(x)→a;当x→+∞时,g(x)→a,于是当且仅当0 2)证明要证x1+x2>2,只要证 x2>2-x1, (1) 由式(1)知0 g(x2)>g(2-x1). 又g(x1)=g(x2),因此只要证 g(x1)>g(2-x1), 即证 a-x1e1-x1>a-(2-x1)ex1-1, 亦即证(2-x1)ex1-1-x1e1-x1>0. (2) 构造h(x)=(2-x)ex-1-xe1-x(其中0 h′(x)=(1-x)(ex-1-e1-x)<0, 从而h(x)在(0,1)上单调递减,于是 h(x)>h(1)=0, 因此式(2)成立,即x1+x2>2. 3)证明显然f(x1)-f(x2)>0.因为 a=x1e1-x1=x2e1-x2, 所以 lna=lnx1+1-x1=lnx2+1-x2, 即 lnx1-lnx2=x1-x2. 又f(x1)-f(x2)= e1-x1-e1-x2+a(lnx1-lnx2)= e1-x1-e1-x2+a(x1-x2), 于是 因此 x1x2<1.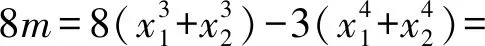
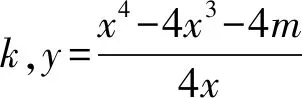
3 精题集萃