致密砂岩气层压裂后产能测井定量预测

陈 烈，郭冀宁，刘财广，王媛媛

(1. 长江大学 油气资源与勘探技术教育部重点实验室，湖北 武汉 430100； 2. 长江大学 地球物理与石油资源学院，湖北 武汉 430100； 3. 中国石油新疆油田分公司 重油开发公司，新疆 克拉玛依 834000)

0 前 言

对储层产能进行定性或定量评价是油气田勘探与开发的一项基本任务[1]。致密砂岩储层具有低孔、低渗特征，基本没有自然产能，一般都需要对其进行压裂改造，提高单井产量和稳产有效期[2-3]，但影响压裂后产能的因素更加复杂，目前测井评价储层压裂后产能具有一定的难度[4-5]。

袁琳、钟家峻、李晓平、吕栋梁等[6-9]研究者对气藏的产能预测进行过研究，但研究的目标主要为储层的自然产能；针对压裂后储层的产能预测的研究则较少。张丽华等[1]通过研究影响压裂后产能的各种参数，提出了神经网络法和方程法，对低孔隙度低渗透率的朝阳沟油田进行了压裂后产能预测，但是其中方程法的参数难以确定。还有一些文献采用例如神经网络、支持向量机等数学方法的进行压裂后储层产能预测[4,10-11]，这种数学方法简单但是缺少实际理论。鞠江慧等[5]利用次生孔隙度、总孔隙度、孔隙结构系数等重要储层参数进行统计分析，总结出适合二连油田低渗透率储层的压裂后产能预测方程，但是统计分析法的地区性较强。

针对鄂尔多斯盆地X地区石盒子组致密砂岩气层压裂后的储层产能测井预测问题，基于渗流力学和毛管理论，推导出储层压裂后每米产气量与有效流动孔隙度呈现指数关系，利用核磁测井可确定储层有效流动孔隙度的优势，建立定量预测模型；考虑岩石可压裂性对储层压裂后产能的影响，确定储层岩石可压裂性的脆性指数下限值，并在定量预测模型中引入脆性指数。本文得到的储层压裂后每米产气量与有效流动孔隙度呈现指数关系的定量预测方程，可以给相同地质研究区的产能预测提供一种思路。

1 地质概况

石盒子组是鄂尔多斯盆地X地区上古生界二叠系产出工业天然气的主要产层之一，沉积环境上部主要发育湖泊和辫状河三角洲沉积，下部主要发育湖泊、河流和辫状河三角洲沉积，有利储集砂体类型为河道、分流河道；储层物性差，孔隙度介于3%～12%之间，渗透率主要介于0.01～3 mD之间，是典型的低渗透储集层[12-13]。

根据研究区铸体薄片资料显示，储层的岩性较为复杂，主要发育岩屑砂岩、岩屑长石砂岩以及长石岩屑砂岩(图1)，其主要岩屑成分为火成岩和变质岩；填隙物主要有四大类，即方解石、硅质、铁矿以及含高岭石、伊利石等的杂基(图2)；孔隙类型主要为溶蚀粒间孔、残余粒间孔、溶蚀颗粒孔以及胶结物溶孔，且次生孔隙为储层主要储集空间，微孔隙发育较少；碎屑颗粒分选中等或较差；磨圆以次棱和次圆为主；支撑类型主要为颗粒支撑；接触方式以凹凸和线—凹凸接触为主。

图1 致密砂岩储层岩性

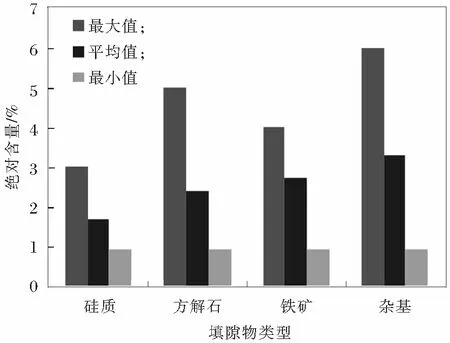
图2 致密砂岩储层填隙物成分

2 储层压裂后产能测井定量预测

对于某一特定的区域，油气性能和外部环境条件相对固定不变，所以储层的产能高低仅仅由油气储层的自身性质决定，但是致密砂岩气层需要经过压裂改造，储层改造效果对产能也有部分的影响，所以岩石可压裂性在进行压裂后产能预测时还应予以考虑。

分储层品质与岩石可压裂性，研究其对致密气储层产能的影响，在此研究的基础上，建立储层压裂后产能测井定量预测模型。

2.1 压裂后产能与储层品质关系

基于渗流力学理论，用于计算产能的平面径向流公式[14]为：

(1)

式(1)中，qf为单位厚度的产出量，m3/(d·m)；Ke为有效渗透率，mD；Q为储层总产出量，m3/d；h为有效厚度，m；c为产能系数；Δp为生产压差，MPa；μ为流体黏度，MPa·s；B为体积系数；re为气井控制半径，m；rw为井底半径，m；S为视表皮系数。测井评价中，假设井外部环境以及油气性能保持一致，产能只与有效渗透率有关。

由毛管理论可知，岩样的有效流动孔隙结构等同于直毛细管孔隙，则有效流动孔隙度与储层渗透率之间存在指数关系[15-16]：

K=aeλφef

(2)

式(2)中，a和λ为系数；φef为有效流动孔隙度，%。

由公式(1)可知储层每米产气量与有效渗透率之间存在线性关系；而由式(2)可知储层有效渗透率和有效流动孔隙度之间存在指数关系。所以当外部条件相同时，可得储层每米产气量与有效流动孔隙度之间存在指数关系。

由于岩石孔隙大小与氢核弛豫率成反比关系，可以利用核磁共振谱(T2谱)研究岩石孔隙[17]。依据流体在岩石中的弛豫时间，可将岩石孔隙中的流体分为束缚流体和可动流体，可以依靠核磁共振测井资料定量评价储层的有效流动孔隙度[17-19]。在计算储层有效流动孔隙度时，选取T2截止值(T2cutoff)是一个关键[20]。图3为研究区21块核磁共振实验确定的T2截止值与孔隙度的关系图，核磁共振实验采用0.690 MPa的离心力。

由图3可以看出：T2截止值的范围较大，介于5～60 ms之间，且难以建立测井评价模型进行精确预测。一方面由于致密砂岩储层非均质性强，T2截止值难以确定，得到完整的离心谱需要离心力大于1.379 MPa[21-22]；而且，由核磁共振岩心实验资料确定的T2截止值，难以用实际测井资料准确表征。所以选取固定的T2截止值计算储层的有效流动孔隙度。

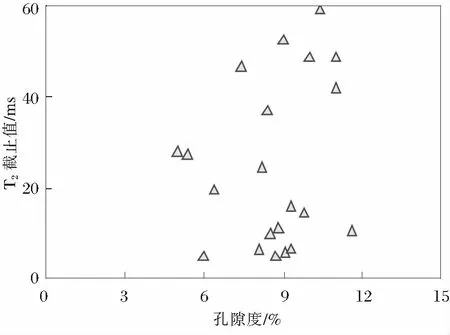
图3 T2截止值与孔隙度关系

在计算有效流动孔隙度时，采用20，33，40 ms 3个不同的T2截止值。然后建立了储层压裂后每米产气量与不同T2截止值计算出的有效流动孔隙度的关系图(见图4)。

图4 储层压裂后每米产气量与有效流动孔隙度关系

由图4可知:33 ms的T2截止值计算的有效流动孔隙度与压裂后每米产气量的相关性要优于20 ms和40 ms两个不同的T2截止值计算的有效流动孔隙度与压裂后每米产气量的相关性。所以，最后确定利用核磁共振测井资料评价储层有效流动孔隙度时的T2截止值采用33 ms。

2.2 压裂后产能与岩石可压裂性关系

压裂后储层产能预测与未压裂储层产能预测的区别就是需要考虑储层压裂效果对产能的影响，国内外众多学者对此也做了很多研究，用岩石的脆性指数来评价可压裂性，反映的是储层压裂后形成裂缝的复杂程度[23]。储层脆性指数越高，其一般性质硬脆。在漫长的地质时期内，由于受构造运动的影响，天然裂缝发育，对压裂作业的反应敏感，能迅速形成一条或多条主裂缝以及多级次生裂缝，这些复杂的网状裂缝使裂缝壁面与储层基质的接触面积最大，使得油气从任意方向的基质向裂缝的渗流距离最短，然而脆性指数低的储层则更容易形成简单的双翼型裂缝[24]。

脆性指数的表征与计算方法有多种[23,25]，本文采用应用最为广泛的Rickman方法[26]，利用阵列声波和密度测井资料计算储层杨氏模量与泊松比，再通过杨氏模量与泊松比归一化处理后计算脆性指数，计算公式详见文献[23]。这里计算的岩石脆性指数，严格来说应该叫做动态脆性指数，评价岩石脆性应该采用岩石力学应力—应变实验确定的静态脆性指数[27]。一般情况下，建立动、静态脆性指数的转换关系以达到利用测井资料计算动态脆性指数评价岩石可压裂性的目的。然而，一方面受限于岩石力学应力—应变实验结果，难以建立有效的动、静态脆性指数的转换关系；另一方面动、静态转换关系大多数均为线性转换，动态指数在很大程度上也可反映岩石可压裂性。因此在鄂尔多斯盆地X地区石盒子组评价岩石可压裂性统一使用基于测井数据计算的测井动态脆性指数，简称测井脆性指数，既可节省岩心实验成本，也可避免动、静态转换的二次误差。

图5为13个测试层的压裂后每米产气量与测井脆性指数关系图。

图5 储层压裂后产能与测井脆性指数关系

由图5可以看出在整体趋势上，储层压裂后产能与测井脆性指数呈现正相关关系，随着测井脆性指数的增大而增大；进一步研究发现，当测井脆性指数小于55%时，储层压裂后产能普遍较低，小于2×103m3/(d·m)，因此可以确定岩石可压裂性的测井脆性指数下限为55%。

2.3 储层压裂后产能测井定量预测

基于上述研究，影响储层压裂后产能的主要因素为有效流动孔隙度，并且两者呈现指数关系；其次岩石可压裂性在一定程度上也影响储层的产能，整体呈现正相关关系。当岩石脆性指数<55%时，储层达不到很好的压裂效果，产能相对较低。

建立储层压裂后每米产气量(具有工业气流的气层)与核磁计算的有效流动孔隙度的关系式(图6a)，具体为:

Q/h=1.032·e0.484φef，R2=0.93

(3)

建立储层压裂后每米产气量与核磁有效流动孔隙度×测井脆性指数的关系式(图6b)，具体为：

Q/h=0.037 5·(φef×BR)-0.776，R2=0.96

(4)

式(4)中，Q/h为储层压裂后每米产气量，103m3/(d·m)；φef为核磁计算的有效流动孔隙度，%；BR为测井脆性指数，%。

在对具有核磁共振测井资料的井进行压裂后储层产能测井预测时，可以利用式(3)模型，简称模型1，进行储层压裂后产能测井定量预测；在对具有核磁共振和阵列声波测井资料的井进行压裂后储层产能测井预测时，可以利用式(4)模型，简称模型2，进行储层压裂后产能测井定量预测。然后将测井定量预测的每米产气量按照储层有效厚度累加起来即为储层的预测总产量。

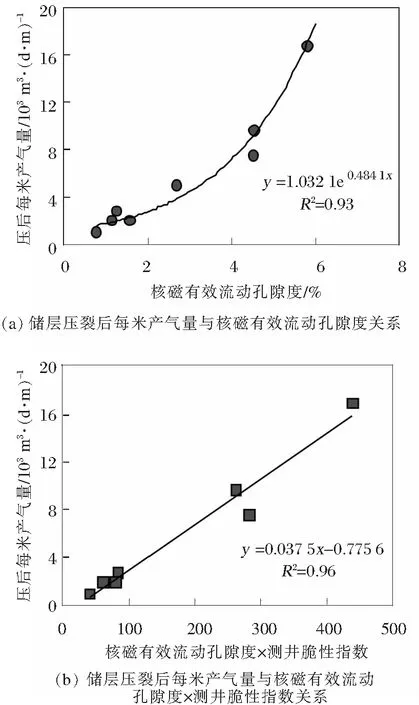
图6 储层压裂后产能测井定量预测模型

3 应用效果分析

将建立的储层产能预测模型应用到鄂尔多斯盆地某一区块石盒子组致密砂岩气储层，图7为B井的部分层段测井解释成果图。

图7 B井部分处理结果

图7中，第1～4道依次为岩性曲线、孔隙度曲线、电阻率曲线和深度，第5道为核磁共振测井T2谱以及T2截止值，第6道为阵列声波测井提取的纵、横波时差，第7道为核磁共振测井33 msT2截止值计算的有效流动孔隙度，第8道为阵列声波与密度曲线计算的测井脆性指数与测井脆性指数下限值，第9道为储层压裂后产能定量模型预测的每米产气量，其中Q/h1为模型1预测的每米产气量，Q/h2为模型2预测的每米产气量，第10道为测井解释结论。图7中，1 514.8～1 519.2 m为测试层段，储层有效厚度为4.4 m，测试结果为压裂后产气，产量为1.21×104m3/d，由于该井该层段进行了核磁共振和阵列声波测井，基于核磁共振测井的模型1测井产能定量预测结果为压裂后总产气1.094×104m3/d，相对误差9.59%；基于核磁共振和阵列声波测井的模型2测井产能定量预测结果为压裂后总产气1.321×104m3/d，相对误差9.17%。

同时将三口井(新测试井)的3个压裂后测试层的测试结果与产能模型预测结果进行对比(表1)，从中可以看出，模型1和模型2预测结果均与测试结论符合很好，压裂后定量预测结果与测试结果的相对误差均在10%以内，验证了模型的可靠性。

表1 致密砂岩气层压裂后产能预测结果

4 结 语

1)依据渗流力学理论和毛管理论，假设井外部环境以及油气性能保持一致的情况下，每米产气量与有效流动孔隙度呈现指数关系；确定阵列测井计算的动态脆性指数(测井脆性指数)为评价致密砂岩气层岩石可压裂性的有效参数，并且确定了55%为鄂尔多斯盆地X地区石盒子组储层岩石可压裂性的下限值。

2)基于核磁共振和阵列声波测井，建立储层压裂后每米产气量测井定量预测模型，应用于鄂尔多斯盆地X地区石盒子组致密砂岩气层的产能预测，预测结果与测试结果符合很好，相对误差均在10%以内，为相同地质区块的致密气藏压裂后产能测井定量预测提供一种思路。