基于高温高压岩电实验的含水饱和度计算模型

黄涛梅，高 颖

(长江大学 地球物理与石油资源学院，湖北 武汉 430100)

0 前 言

在储层测井综合评价中，岩电参数计算准确与否尤为重要[1-2]。其中胶结指数m值和饱和度指数n值一直是学者分析的重点，他们值的变化会影响含水饱和度的计算，从而影响到油气储量计算，还会对流体性质识别和储层的客观评价造成影响[3]。在传统理论中，m，n主要是受到岩性和孔隙结构的影响，因而在常规测井解释中直接将理论值或者岩心测试实验得到的实验值用于测井解释参数模型的构建。但是这两个参数不仅仅受到岩性和孔隙结构影响，地层水矿化度，围压，温度这些条件也影响m，n值的确定。而在岩心测试过程中通常是常温常压条件，常温常压岩电实验指在地表温压条件下进行岩电数据测量，由于实际地层压力、温度与地表压力、温度存在较大差异，在常温常压条件下得到的岩电参数不能反映地层真实情况。因此在实验室中模拟地层高温高压条件进行岩电实验，得到的岩电参数更加准确，然后结合实际井计算的含气饱和度更加接近于地层实际[4-6]。

1 常温常压和高温高压实验的分析

如图1～2所示，是A区块A井深度4 327.1 m处的一块岩心分别在常温常压和高温高压条件下的

图1 高温高压岩电测试

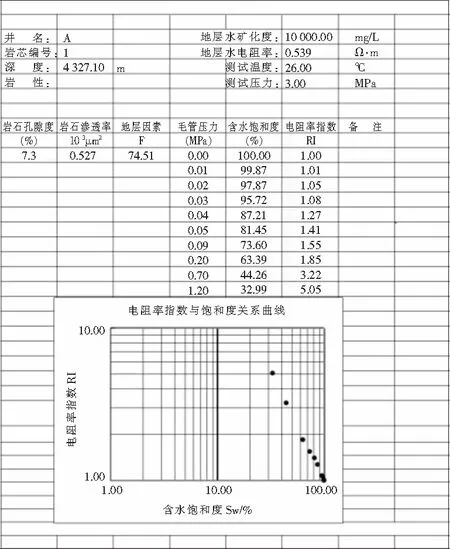
图2 常温常压岩电测试

岩心实验数据。对比同块岩心在不同实验条件下的数据，孔隙度、渗透率、地层因素等重要参数都有较大区别。

图3～4为利用A井高温高压条件下岩电实验结果和常温常压条件下岩电实验结果制作的地层因素与孔隙度、电阻率指数与含水饱和度的关系对比图。

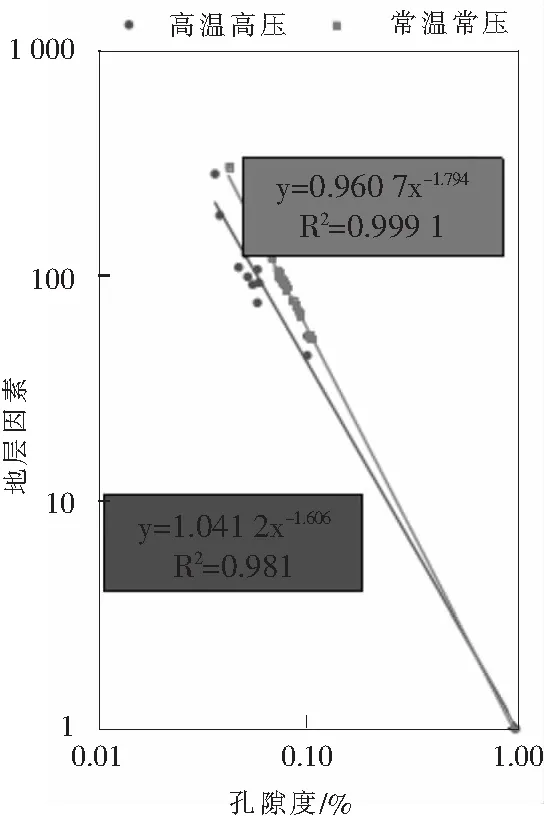
图3 地层因素与孔隙度关系

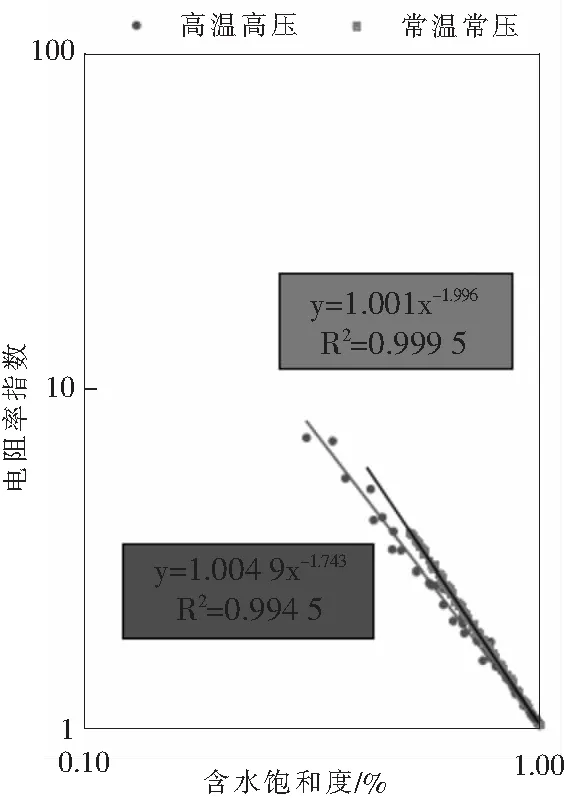
图4 电阻率指数与含水饱和度关系

由图3中地层因素与孔隙度关系拟合确定：高温高压条件下，a=1.041 2，m=1.606；常温常压条件下，a=0.960 7，m=1.794。

由图4中电阻率指数与含水饱和度关系拟合确定：高温高压条件下，b=1.004 9，n=1.743；常温常压条件下，b=1.001，n=1.996。

可以看出：高温高压和常温常压实验条件下获得的岩电参数有较大差异。

2 含水饱和度计算模型

由于A区储层电阻率受到泥质含量的影响较大，其值明显低于正常气层水平，对于含水饱和度的准确计算有较大影响，因而在计算低渗气层的含水饱和度时，应考虑泥质含量的影响，本次在岩电实验资料的基础上，采用西门杜公式计算含水饱和度[7-9]：

(1)

式(1)中，Rsh——泥岩电阻率，Ω·m；Vsh——泥质含量；其中alfa为经验值，这里取1.5。

当利用式(1)计算含水饱和度时，需重新利用式(1)回归岩电参数。

由式(1)可得到(Sw=1时Ro=Rt)：

(2)

将式(3)带入式(2)，根据阿尔奇公式中得到：

(3)

由式(3)可知，若考虑泥质含量的影响，a与m值将与由阿尔奇公式得到的不同。因此需要利用公式(3)重新回归a值与m值。在这一过程中，各样品的泥质含量用的是实验室分析的结果，表1为A地区A井H3段高温高压西门杜公式回归岩电参数表。

表1 A区块A井H3段高温高压西门杜公式回归岩电参数

表1中：

利用表1回归可得出A井H3层段关系式为：

y=0.924 4φ1.614 1

(4)

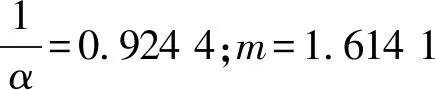
表2为A地区A井H3段西门杜公式回归岩电参数表。

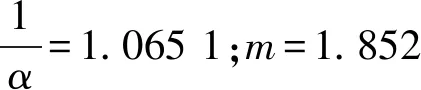
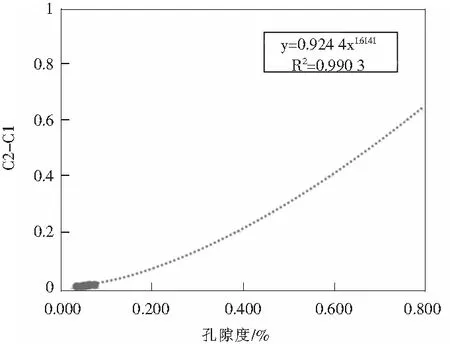
图5 A区块A井H3段高温高压条件下C2-C1与孔隙度关系

图6 A区块A井H3段砂岩组常温常压条件下C2-C1与孔隙度关系

表2 A区块A井H3段常温常压西门杜公式回归岩电参数

3 应用效果分析

图7为A井3 494.5～3 528 m深度段测井解释成果图，该段结合气测结果、三孔隙度差值等信息，确定为气层。图中对利用不同温压条件岩电参数、不同饱和度模型计算得到的含水饱和度进行了对比。

由图7可以看出：原常温常压岩电参数计算得到的含水饱和度明显偏大；高温高压条件计算得到的含水饱和度和岩心密闭取心刻度含水饱和度吻合较好，说明高温高压岩电参数更加适合本地区。由于该层段泥质含量较低，高温高压西门杜公式和高温高压阿尔奇公式的到的含水饱和度差异并不明显。

图8为A井4 320～4 360 m深度段测井解释成果图，图中对利用不同温压条件岩电参数、不同饱和度模型计算得到的含水饱和度进行了对比。

图7 A井3 494.5～3 528 m层段含水饱和度结果对比

图8 A井4 320～4 360 m层段含水饱和度结果对比

由图8可以看出：典型气层段中使用高温高压岩电参数计算得到的含水饱和度和束缚水饱和度差别更小，使用高温高压岩电参数计算得到的含水饱和度更为合理；在4 330～4 340 m泥质含量较高的层位，泥质含量对饱和度影响很大，因此必须考虑泥质的影响选择西门杜模型，图中显示西门杜公式计算得到的含水饱和度比阿尔奇公式计算得到的含水饱和度更为合理。

4 结 论

1)基于高温高压岩电参数，利用变m值西门度公式可有效计算低渗复杂储层的含水饱和度，与定m值计算结果相比，计算结果更符合DST测试结论，计算精度更高，与实际情况更相符；

2)泥质含量较高时，高温高压岩电参数西门杜公式计算含水饱和度精度更高。