利用时空轨迹挖掘移动对象聚集移动模式
史覃覃,韩文军,陶 宁,吉根林,赵 斌,黄潇婷
1(南京师范大学 计算机科学与技术学院,南京 210023)2(国网经济技术研究院有限公司,北京 102209)3(山东大学 旅游管理系,济南 250100)
1 引 言
随着全球定位技术和无线通讯技术的发展,移动终端(如GPS设备、智能手机等)产生了海量的移动对象时空轨迹数据.分析和研究这些数据,可以发现移动群体在时空上的运动规律和行为模式[1].聚集模式研究移动对象群体在时空上的聚集运动规律,可以监控和预测不寻常的群体事件,如游行、交通拥堵、商业活动等[2].近几年来学术界针对轨迹数据上的聚集事件发现[3-5]展开了研究.2002年Laube等人提出了汇聚模式(Aggregation)[6],根据移动对象从四周向中心圆形区域集中的运动形态发现聚集过程.2013年Zheng等人结合密集区域的概念,提出了聚合模式(Gathering)[7,8],用于发现一段时间内空间上保持稳定且足够密集的移动对象群体.2014年Guo等人提出了滚雪球模式(Snowball+)[9],根据相邻时刻群体的重叠数量和规模变化发现聚集过程.2015年Hong等人利用拓扑结构研究聚集问题,提出了黑洞模式(Black Hole)[10],根据子图中人群的进出流量之差识别聚集行为.2017年Lan等人在聚合模式的基础上提出了演变群体模式(Evolving Group)[11].
不难发现,上述聚集模式研究均是从检测聚集的角度,对群体形成聚集之前的运动形态建模,并不能反映群体在聚集后的运动和变化规律.汇聚模式、滚雪球模式和黑洞模式识别的是群体形成聚集的动态汇聚过程;聚合模式识别的是群体连续稳定的聚集状态,它们均不关注已聚集的移动对象群体,无法描述其在时空上的变化和行为规律.演变群体模式虽然关注移动对象的演变规律,但是没有考虑邻近时刻群体之间的关联性,并且对固定的时间窗口内模式的连续性没有要求.因此,该模式不适用于静态数据上完整连续的聚集运动的发现.但是,在现实生活中,追踪参与聚集的移动对象群体,研究其行为模式,具有重要的实际应用价值.它可以帮助人们检测和监控感兴趣的聚集对象,提供决策支持,如犯罪团伙追踪、动物习性研究、旅行线路推荐等.为了完整地刻画聚集群体在时空上的运动变化,本文提出聚集移动模式(Aggregation Moving Pattern,简称AMP).
聚集移动模式针对聚集群体的移动规律建模,与传统聚集模式相比,其在成员和时间维度都进行了相应的“放松”[12,13],更符合现实生活中的应用场景.在成员方面,聚集移动模式只要求邻近时刻移动对象群体有一定比例的重叠,在允许对象中途加入或离开的同时,保证了邻近时刻聚集群体的局部稳定性.在时间方面,不要求严格连续,允许有较短时间间断,以适应聚集群体更多的时空行为变化.因此,聚集移动模式可以识别更完整、丰富、可变化的聚集运动行为.
基于以上分析,聚集移动模式挖掘主要面临以下两个问题.首先,群体运动具有复杂性.在现实场景中,参与聚集的移动对象运动状态多样,且在时空上的运动关系也很复杂,这对聚集群体的运动行为建模增加了难度.其次,模式挖掘代价高.当面临大规模的轨迹数据,对每个时刻的所有簇进行处理时,搜索空间巨大,从而使得聚集移动模式挖掘代价很高.
为了应对上述问题,在聚集移动模式的定义中引入集合相似关系[14-17],用来识别邻近时刻聚集群体之间的关联性.利用连接操作,实现聚集移动模式的挖掘.基于以上思路,提出并实现了聚集移动模式挖掘框架AMPM,使用简单的循环遍历实现簇相似连接.为了提升挖掘算法的时间性能,本文对连接操作进行了优化.利用移动对象群体之间的成员关系,提出前缀过滤-验证框架,缩小搜索空间,分别实现了基于前缀倒排索引的AMPM_PI算法和基于前缀划分索引的AMPM_PP算法.为了进一步缩小候选集规模,利用长度和位置信息对上述算法进行剪枝.在实验部分,采用真实的游客和出租车轨迹数据进行实验,结果表明本文提出的挖掘算法在挖掘效果和算法效率方面是可行的.
2 相关定义
定义1.(时空轨迹)设移动对象集合ODB={o1,o2,…,on},时间域TDB={t1,t2,…,tm},对象o的时空轨迹表示为o.traj=<(pt1,t1),(pt2,t2),…,(ptm,tm)>,其中o∈ODB,(pti,ti)表示o在ti时刻的采样点,pti=(xti,yti)∈R2表示o在ti时刻的空间位置,xti表示空间位置所在的经度,yti表示空间位置所在的纬度,ti∈TDB.


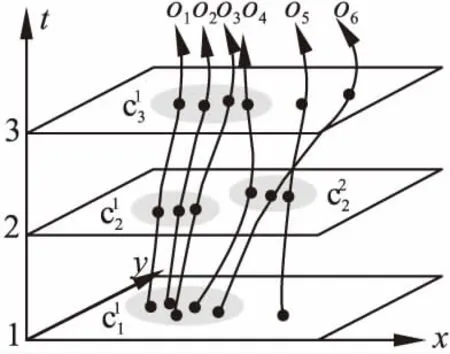
图1 移动对象快照簇示例Fig.1 Example of snapshot clusters
定义3.(簇相似关系)给定成员重叠率δ,簇间距离阈值d,ti和tj时刻的两个簇cti和ctj,如果满足以下两个条件,则称簇cti和ctj具有相似关系,记作:cti∽ctj,(cti,ctj)表示一个簇对.
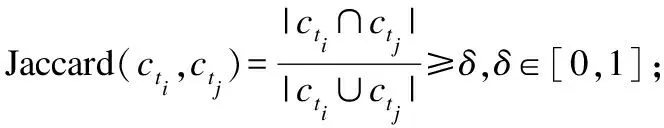
2)空间相近:利用Hausdorff距离度量两个簇之间的空间距离,Hausdorff(cti,ctj)≤d*Δt,Δt=|j-i|.

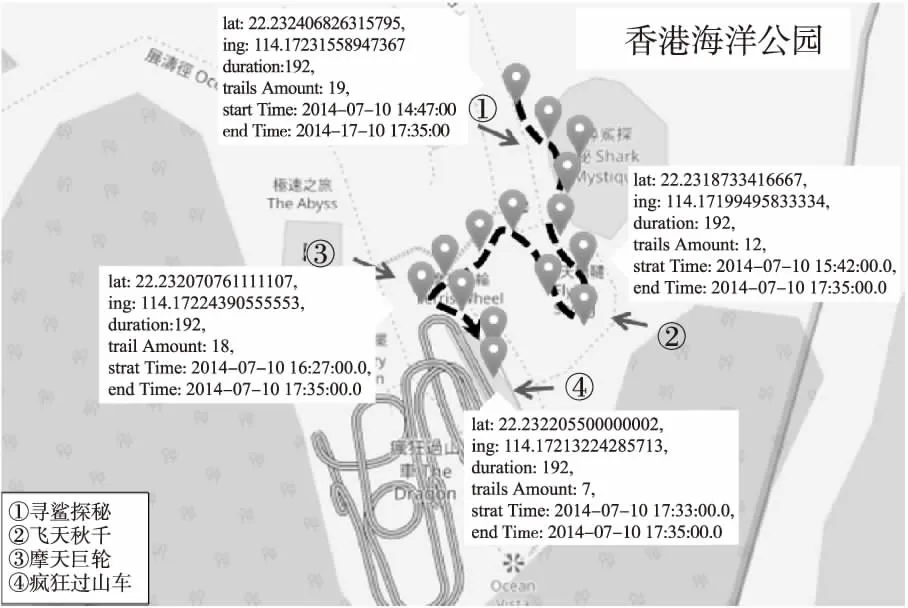
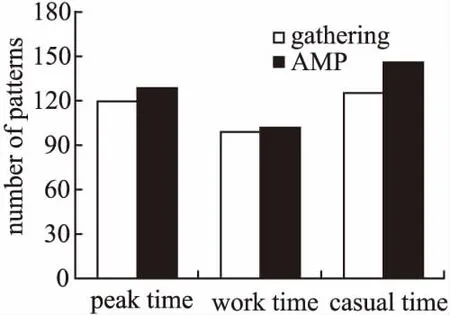
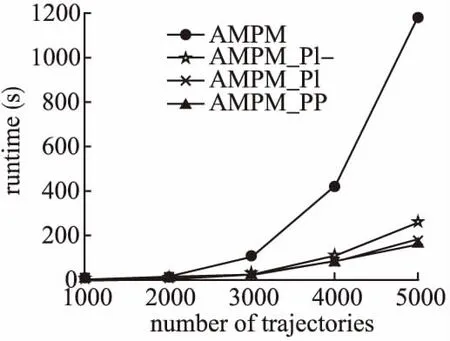
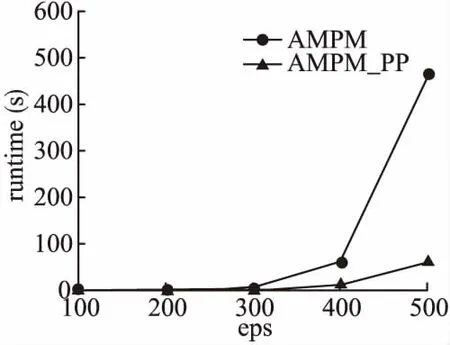
定义4.(聚集移动模式)给定生存期阈值k,时间间断阈值g,持续时间阈值L,聚集移动模式表示为簇的序列,即AMP: 1)生存期:模式生存期AMP.lifetime=c-a+1≥k. 2)可间断性:T中任意两个相邻的时间戳tm和tn,满足|m-n|≤g. 3)时间局部持续性:∀T′⊂T,T′={td,td+1,…,te}为T中连续的时间戳集合,满足|T′|=e-d+1≥L. 4)运动稳定性:C中任意两个相邻的簇ctm和ctn,满足簇相似关系,即ctm∽ctn. 如果一个聚集移动模式AMPi,不存在另一个聚集移动模式AMPj,使得AMPi⊂AMPj,则称AMPi是闭合的. 图2 聚集移动模式示例Fig.2 Example of aggregation moving pattern 给定移动对象集合ODB,时域TDB,生存期阈值k,群体规模阈值m,时间间断阈值g,持续时间阈值L,成员重叠率δ和簇间距离阈值d,时空轨迹聚集移动模式挖掘的目标是在时域TDB内发现轨迹集合中所有闭合的聚集移动模式. 基于闭合聚集移动模式的定义,本文提出聚集移动模式挖掘框架AMPM(Aggregation Moving Pattern Mining),主要包括以下四个阶段. 1)轨迹预处理 真实的时空轨迹数据采样频率并不相同,因此轨迹长度往往不等.预处理阶段的主要任务是采用线性插值等方法将不等长的轨迹基于相同的时域进行“对齐”和“补全”. 2)移动对象聚类 在时域TDB中的每一个时间戳上,利用基于密度的聚类方法对移动对象群体ODB进行聚类. 3)簇相似连接 利用成员相似和空间相近条件识别两个不同时刻的簇集合中所有具有簇相似关系的簇对,此操作称为簇相似连接.令R、S为两个不同时刻的簇集合,|R|=N,|S|=M,R和S之间的簇相似连接操作定义为R▷◁∽S={(r,s)|r∽s,r∈R,s∈S}. 4)聚集移动模式识别 在时域TDB中识别出所有的具有簇相似关系的簇对,生成候选模式.然后,验证这些候选模式是否满足闭合聚集移动模式的定义,从而找出所有闭合的聚集移动模式. 聚集移动模式挖掘框架AMPM完整的挖掘过程如算法1所示.首先,在每一个时刻,进行基于密度的聚类并获得有效快照簇集合(4-6行).接着,对每一个候选者的簇序列中最后一个快照簇(即p.lastcluster)进行簇相似关系搜索,实施连接操作(8行).然后,判断该候选者是否能被扩展,若能,则扩展当前候选者,并将其作为新的候选模式加入候选集(9-12行).否则,进行条件判断和模式验证.若满足间断条件,则更新该候选模式的间断时间(13-15行).否则说明该候选者不能再进一步扩展(已封闭),则进行聚集移动模式验证(16-18行).最后,当前时刻未被分派的快照簇可能在后续时间形成聚集移动模式,因此,要将当前时刻所有未被分派的快照簇作为新的候选者加入候选集(20行). 算法1.聚集移动模式挖掘框架(AMPM) 输入:移动对象集合ODB,生存期阈值k,群体规模阈值m,簇间距离阈值d,成员重叠率δ,持续时间阈值L,时间间断阈值g,邻域半径阈值eps,邻域密度阈值minPts 输出:聚集移动模式集合AMP 聚集移动模式挖掘算法的核心操作是对两个邻近时刻的簇集合进行相似连接,在此过程中,最耗时的部分是簇相似关系搜索(SearchCluster函数).本文针对该部分提出基本算法并进行相应改进. 3.2.1 簇相似关系搜索基本算法 利用简单的循环遍历就可以对两个不同时刻的簇集合进行簇相似关系搜索,实现连接操作,这是簇相似关系搜索的基本算法.该算法搜索过程如算法2所示,使用简单的遍历,对快照簇集合进行簇相似关系搜索(2-6行).其中,利用该搜索方法进行连接操作的时间复杂度为O(N*M),N和M分别表示两个时刻簇集合的规模.聚集移动模式挖掘算法AMPM需要在n个连续的时刻利用基于循环遍历的基本算法完成连接操作,算法的时间复杂度为O(n*N*M),代价太高. 算法2.簇相似关系搜索基本算法 输出:目标簇ctarget 3.2.2 基于前缀倒排索引的簇相似关系搜索改进算法 给定δ=0.8,|r|=10,|s|=9,若Jaccard(r,s)≥δ,则一定有相同对象个数Overlap(r,s)≥9. 引理2.给定两个簇r和s,设Prefix(r)为r中长度为⎣(1-δ)|r|」+1的前缀,Prefix(s)为s中长度为⎣(1-δ)|s|」+1的前缀.如果Jaccard(r,s)≥δ,则有Prefix(r)∩Prefix(s)≠∅. 给定δ=0.8,簇r={o1,o2,o3,o5,o7,o8},则r中长度为⎣(1-δ)|r|」+1=2的前缀Prefix(r)={o1,o2}. 1)前缀过滤-验证框架 前缀过滤-验证框架的过程如图3所示.首先,根据引理2获得簇集合S中所有簇的前缀,并对前缀建立(移动对象-簇)索引.接着,对待搜索簇r 的前缀中所有对象,利用索引获得初步候选集(步骤1,2).然后,利用长度和位置剪枝策略对初步候选集进一步剪枝,获得最终候选集(步骤3).最后,对候选集中所有候选者进行簇相似关系验证,以得到最终匹配上的簇对(步骤4).在前缀过滤-验证框架下,为了加快前缀搜索过程,本文设计了两种索引结构对S集合建立索引,分别提出了基于前缀倒排索引的簇相似关系搜索改进算法和基于前缀划分索引的簇相似关系搜索改进算法. 图3 前缀过滤-验证框架Fig.3 Prefix filter-verification framework 在前缀过滤的基础上,本文还提出两种剪枝策略,进一步减少候选集规模,减少无用簇的相似关系计算,加快连接速度. 2)长度剪枝策略 利用簇中群体的规模(即簇的长度)进行剪枝,如引理3所示,直接将候选集中长度不满足条件的簇过滤掉. 给定δ=0.8,|r|=10,则与簇r具有簇相似关系的簇s的长度范围为8≤|s|≤12. 3)位置剪枝策略 利用簇中移动对象的有序性,根据前缀中相同对象所处的位置,对候选集中的簇进一步剪枝.如图4所示,簇对(r,s)已通过前缀过滤和长度剪枝,阴影部分为其前缀.给定δ=0.8,由引理1可知,r和s具有簇相似关系的必要条件是相同对象个数Overlap(r,s)≥9.首先,对r和s前缀中的移动对象进行依次匹配,第一个匹配上的是位置2.此时可知,s和r中最多能有8个共同对象,不满足Overlap≥9的条件,因此该簇对被剪枝. 图4 位置剪枝过程Fig.4 Process of positional pruning 算法3.基于前缀倒排索引的簇相似关系搜索改进算法 输出:目标簇ctarget 利用前缀过滤-验证框架进行簇相似关系搜索,并通过建立倒排索来引加快前缀搜索过程,如算法3所示.首先,根据引理2计算获得所有簇的前缀,并对前缀建立(移动对象-簇)倒排索引(2-4行).然后,对待搜索簇的前缀cpre中的每一个对象,遍历索引表,获取对应的索引项,并将其作为该簇的候选者(5-7行).接着,进行长度和位置剪枝(8-9行).最后,对所有候选者进行簇相似关系验证,并返回最终结果(10-14行).使用该搜索方法进行连接操作最好情况下的时间复杂度为O(N*|r|avg),最坏情况下为O(N*M).虽然使用上述搜索算法进行聚集移动模式挖掘(AMPM_PI算法)最坏情况下的时间复杂度仍然是O(n*N*M),但是由于该算法大大缩小了搜索空间,降低了候选集的规模,因此挖掘效率明显提升. 3.2.3 基于前缀划分索引的簇相似关系搜索改进算法 算法3采用倒排索引结构减小搜索空间,加快前缀搜索过程.但是,索引表规模比较大,约M*(1-δ)|s|avg.调用索引时,需要重复遍历扫描索引表.该过程是非常耗时的,导致算法3在最坏情况下的时间复杂度为O(N*M).由于在同一时刻一个对象最多只属于一个簇,所以(移动对象-簇)索引表中每一项只有一个簇.基于这一性质,本文提出了基于前缀划分索引的簇相似关系搜索改进算法.在前缀过滤的基础上对前缀中的移动对象进行划分,利用划分方法将搜索空间减小.该算法主要思想是,给定整数e,对S集合的前缀中每一个对象生成一个值(对象id模e取余),然后将该对象所在的簇划分到这个值对应的分区中.此划分策略将索引规模降为固定的e项,且查找索引的时间代价降为O(1). 算法4.基于前缀划分索引的簇相似关系搜索改进算法 输出:目标簇ctarget 根据算法思想可知,S集合的前缀中约M*(1-δ)|s|avg个移动对象需要划分到e个分区中,考虑尽可能让每个分区大小相同,则e=a*M*(1-δ)|s|avg,其中系数a∈(0,1),可根据具体实验环境和数据集进行设置. 在前缀过滤-验证框架下,通过前缀划分策略进行簇相似关系搜索的过程如算法4所示.首先,与算法3相同,获得簇的前缀(2-3行).接着,将S集合前缀中的对象划分到e个分区(4行).然后,对待搜索簇的前缀中的每一个对象,获取对应分区中的簇,作为候选者(5-7行).最后,与算法3相同,进行剪枝和验证.使用该搜索方法进行连接操作的时间复杂度为O(N*|r|avg),与分区数e无关.使用该算法进行聚集移动模式挖掘(AMPM_PP算法)的时间复杂度为O(n*N*|r|avg),与算法3最好情况下的时间复杂度相同. 为了验证本文提出的聚集移动模式挖掘算法的有效性和高效性,利用两个真实的GPS轨迹数据集进行实验,见表1.经过轨迹预处理后,Tour 和Taxi数据集的时间区间均以分钟为单位. 表1 数据集说明 DatasetsTrajectoriesSampleSizeTour1201min32.8MBTaxi130001min8.41GB 游客轨迹数据集(Tour):香港海洋公园120名游客每天10:00am(开馆时间)到20:00pm(闭馆时间)的移动轨迹数据.(2014年7月6日-10日,五天) 出租车轨迹数据集(Taxi):上海市13000辆出租车全天的GPS轨迹数据.(2015年4月1日-7日,一周) 实验程序使用Java语言编写,操作系统为Windows10 64,硬件环境为Intel(R)Core(TM)i5-6500 CPU,主频3.20HZ,4GB内存. 本文将从模式定义的有效性和挖掘算法的效率两个方面对聚集移动模式进行评价.实验聚类方法采用经典的DBSCAN算法. 有效性实验使用Tour 和Taxi数据集,分为两组进行. 首先介绍实验参数设置情况,见表2,括号内为Taxi数据集的参数值,括号外为Tour数据集的参数值.参数说明如下:邻域密度阈值minPts,邻域半径阈值eps,模式生存期阈值kt,群体规模阈值mc,簇间距离阈值d,参与者生存期阈值kp,参与者数量阈值mp,成员重叠率δ,时间间断阈值g,持续时间阈值L. 表2 各模式挖掘方法的参数设置 MethodsParameter settingsDBSCANminPts=5(5),eps=40(200)Gatheringkt=10(10),mC=10(15),d=50(300),kp=8(8),mp=8(10)AMPkt=10(10),mC=10(15),d=50(300),δ=0.7(0.7),g=2(3),L=4(2) 第一组实验进行实例的可视化分析.为了展示更好的可视化效果,本组实验放宽时间阈值,令kt=120,g=60,L=30,其它参数设置同表2.以Tour数据集中7月10日产生的聚集移动模式挖掘结果为例,选取其中一个聚集移动模式进行可视化,如图5所示.图中每一个图钉表示一个簇中心,一组图钉序列表示一个聚集移动模式.观察该模式的整个生存期可以发现,一群游客从寻鲨探秘海洋馆开始游玩,途径飞天秋千、摩天巨轮,最后到达疯狂过山车,且游客的移动路径与公园中的实际道路相符.同时,还可以看出,游客在游玩每个项目时,都需要在门口排队,游玩时间基本在半小时到一小时之间,这也与公园中的实际场景相符.上述提到的四个项目都是香港海洋公园中网友推荐指数较高的游乐项目,容易发生游客聚集.由于这四个项目的距离较近以及公园中的道路情况,游客采取的游玩路线也基本相同,因此容易发生游客群体的聚集移动事件.上述的实例分析表明,本文挖掘出的聚集移动模式与现实场景相吻合,可以帮助人们追踪游客群体,发现其运动趋势和移动规律,从而为旅游推荐、旅游管理等提供决策支持. 图5 香港海洋公园的一个聚集移动模式Fig.5 Visual aggregation moving pattern at Hongkong Ocean Park 第二组实验比较聚集移动模式与聚合模式挖掘结果的数量和平均长度.将一天划分成三个时间段,分别为:高峰时间段(6:00am-10:00am和17:00pm-20:00pm)、工作时间段(10:00am-17:00pm)和休闲时间段(20:00pm-03:00am).使用Taxi数据集进行实验,参数设置同表2.聚集移动模式和聚合模式一周的挖掘结果平均数量对比,如图6所示.可以看出,在休闲和高峰时间段有较多的聚集移动模式,而在工作时间段的模式较少,这与上海市的实际交通情况相符.在每天的上下班高峰时间段,会发生较多的交通拥堵.上海的夜生活比较丰富,因此在休闲时间段,人们出行较多从而容易发生聚集.相反地,在工作时间段,人们出行较少且交通流量较小,因此产生的聚集事件也较少.从图6、图7可以看出,在一天的三个时间段中,聚集移动模式挖掘结果的数量和平均长度均高于聚合模式,说明聚集移动模式比聚合模式识别到更多更完整的聚集运动.存在这样的差距,主要原因在于聚合模式识别的是时间连续且区域相对稳定的“静态”聚集,因此发现的往往是长时间的严重的交通堵塞.而本文提出的聚集移动模式关注的是聚集群体的运动和变化规律.除了严重的拥堵外,它还可以追踪短生存期的聚集车辆,监控它们的拥堵状态是变得更严重还是稍有缓解.另外,时间的可间断性,使得聚集移动模式能够更灵活的刻画更多场景下的运动行为. 图6 模式挖掘结果的数量的比较Fig.6 Comparison of the number of pattern mining results 图7 模式挖掘结果的平均长度的比较Fig.7 Comparison of the average length of pattern mining results 本文提出的聚集移动模式研究尚未见文献报道,因此在算法时间效率方面无法与已有方法进行对比. 效率实验使用Taxi数据集对聚集移动模式挖掘算法进行分析,分为三组进行.第一组实验对比本文提出的簇相似连接基本算法AMPM、基于前缀倒排索引的簇相似连接改进算法AMPM_PI和基于前缀划分索引的簇相似连接改进算法AMPM_PP的时间性能.选取Taxi数据集中4月1日的轨迹数据作为本组实验测试数据,参数设置同表2.AMPM算法和AMPM_PI、AMPM_PI-(未使用长度和位置剪枝策略的AMPM_PI)、AMPM_PP算法的连接操作在不同轨迹量下执行时间的对比,如图8所示.从图中可以看出,AMPM与AMPM_P系列算法的时间性能存在明显差距,AMPM_P系列算法要远优于AMPM算法,其中,AMPM_PP算法时间性能最好.并且,轨迹数量对AMPM算法的执行时间影响很大而对AMPM_P系列算法影响较小.特别是当轨迹数量较大时,AMPM算法连接操作的执行时间急剧增大.这是由于随着轨迹量的增大,每个时刻的簇集合规模增大,连接操作的执行时间也相应增大.AMPM算法利用循环遍历进行簇相似关系搜索,因此,受簇集合规模的影响较大.而AMPM_P系列算法通过前缀过滤,大大减少了搜索空间,因而簇集规模对其影响较小.从图8中也可以看出,随着轨迹量的增大,两个剪枝策略的优势也越来越明显.这是由于随着轨迹量的增大,候选集规模也随之增大,剪枝的效果也更加凸显. 图8 轨迹数对连接操作执行时间的影响Fig.8 Impact of execution time of join operation on number of trajectories 第二组实验比较DBSCAN的两个参数(邻域密度阈值minPts和邻域半径阈值eps)对AMPM和AMPM_PP算法连接操作执行时间的影响.截取Taxi数据集中4月1日8000辆出租车早高峰段(7:00am-9:00am)的轨迹数据作为本组实验的测试数据,实验参数同表2.两个算法连接操作执行时间随邻域密度的变化情况,如图9所示;连接操作执行时间随邻域 图9 邻域密度对连接操作执行时间的影响Fig.9 Impact of execution time of join operation on neighborhood density 图10 邻域半径对连接操作执行时间的影响Fig.10 Impact of execution time of join operation on neighborhood radius 半径的变化情况,如图10所示.本组实验中没有计算DBSCAN算法的执行时间,但是不同参数下的聚类算法会导致当前时刻簇集合的规模发生变化,从而对连接操作的执行时间产生影响.从图9、图10中可以看出,DBSCAN参数对AMPM算法的影响很大,而对AMPM_PP算法几乎没有影响.说明AMPM_PP算法对DBSCAN参数不敏感,时间性能明显优于AMPM算法. 第三组实验比较群体规模阈值m对AMPM和AMPM_PP算法连接操作执行时间的影响,如图11所示.实验数据和参数与第二组实验相同.群体规模阈值影响每个时刻簇集合的规模,从而影响连接操作的执行时间.从图11中可以看出,AMPM算法受群体规模阈值的影响较大,而AMPM_PP算法几乎没有影响.说明AMPM_PP算法对群体规模阈值不敏感,时间性能优于AMPM算法. 图11 群体规模对连接操作执行时间的影响Fig.11 Impact of execution time of join operation on cluster size 本文利用时空轨迹挖掘移动对象的聚集移动模式.首先,提出并实现了利用基本算法进行簇相似连接的聚集移动模式挖掘框架AMPM算法.为了提升挖掘算法的时间性能,在前缀过滤-验证框架的基础上,提出并实现了基于前缀倒排索引的AMPM_PI算法和基于前缀划分索引的AMPM_PP算法.为了进一步缩小候选集规模,提出了两种剪枝策略.通过有效性实验验证了聚集移动模式在挖掘效果方面的优势;对比挖掘框架的基本算法及其改进算法的时间性能,验证了本文提出的改进算法在性能方面的优势.未来工作主要考虑基于轨迹流上的聚集移动模式的研究.

3 算法设计
3.1 聚集移动模式挖掘框架

3.2 簇相似关系搜索




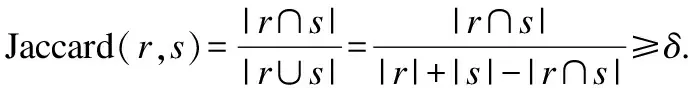


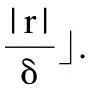






4 实验与结果分析
4.1 实验设计
Table 1 Statistics of datasets
4.2 挖掘结果有效性
Table 2 Parameter settings of pattern mining methods

4.3 算法时间效率


5 结束语

