利用前景理论的不确定QoS感知Web服务选择
严 华,付晓东,2,岳 昆,刘 骊,刘利军
1(昆明理工大学 信息工程与自动化学院云南省计算机技术应用重点实验室,昆明 650500)2(昆明理工大学 航空学院,昆明 650500)3(云南大学 信息学院,昆明 650091)
1 引 言
Web服务是具有自描述、模块化等特点的Web应用程序,目前已成为面向服务的体系结构(Service-Oriented Architerture,SOA)的最佳支撑技术.近年来,随着Web服务技术的飞速发展,网络上出现大量功能相同或相似的Web服务,但是它们的服务质量(Quality of Service,QoS)会出现不尽相同的情况.因此在服务选择过程中,QoS成为选择Web服务的关键因素.
由于网络环境的开放性,Web服务的QoS属性如响应时间、吞吐量、可靠性等容易受到用户的网络状况、服务负载、位置等因素的影响,导致Web服务的QoS属性存在不确定情况,这就使得如何选择满足用户QoS需求的服务成为一个具有挑战性的问题:首先,由于QoS信息的不确定性,使得用户面临所获取的服务不能满足其需求的风险,因此在进行Web服务选择时面对QoS不确定的情况,需要考虑用户的风险态度如风险偏好[1]等因素.其次,由于内部状态和外部环境等因素的不同,同一服务内的QoS属性以及不同服务间的QoS属性分布概率都不尽相同,因此在不确定QoS条件下Web服务选择中假设QoS属性为特定分布情况[2,3]不符合实际情况.
为解决上述问题,提出一种基于前景理论(Prospect Theory,PT)[4,5]的不确定QoS感知的Web服务选择方法,利用前景理论作为基础,在QoS不确定以及QoS不符合特定分布概率的条件下根据用户QoS需求、选择服务时的风险态度进行Web服务选择的问题.
2 相关工作
QoS感知的Web服务选择策略主要分为局部最优[6,7,10,11-13]策略和全局最优[8,9,14-16]策略.局部最优策略只考虑满足局部选择的最优解,而没有考虑全局服务选择约束;全局最优策略考虑服务组合后的全局最优效果,而较少关注局部服务选择结果的优劣.
局部最优策略的基本思想是:在每个任务节点的候选服务集合中,依据QoS约束条件,选出最优的局部服务.文献[10]提出将Skyline计算引入到服务选择中,但只考虑服务QoS信息为确定值条件,并不能应用于QoS不确定场景下的服务选择.而针对Web服务的QoS不确定情况,文献[11]提出了一种基于FAHP的多维QoS局部最优服务选择模型.该方法在选择Web服务时仅考虑QoS属性.文献[12]考虑Web服务的QoS区间和用户需求,文献[13]通过使用均值标准差描述QoS指标来体现QoS动态变化下服务查询选择的风险,但该方法没有考虑到用户选择服务时的风险态度.并且在选择Web服务的过程中上述研究方法未能将这两个因素综合考虑,因此选择的结果不能充分体现用户需求和风险态度因素.
全局最优策略的基本思想是:从单个服务的选择变为整个组合服务的选择,使选出的服务能更加满足用户对组合服务的要求.文献[14,15]研究基于SOA建立可靠性的Web服务组合方法,着重解决动态环境下的Web服务选择.针对QoS信息不确定的情况,文献[16]根据粒子群算法,提出一种PSO-GODSS算法用于解决组合服务中QoS全局最优动态Web服务选择问题.上述研究方法选择的服务是满足QoS约束条件的目标最优解,而不是在最大程度上满足用户需求的服务.
考虑以上研究存在的不足,本文在QoS不确定情况下,将用户对QoS属性需求作为关键因素,通过比较用户需求与Web服务QoS属性关系得出风险收益矩阵和风险损失矩阵,考虑用户的风险态度,通过前景理论来解决QoS不确定条件下的Web服务选择问题.最后,本文通过实验验证该方法的合理性和有效性.
3 问题描述
首先对QoS不确定条件下的Web服务选择问题描述如下:
定义1.候选服务集合为S={s1,s2,…,sm},其中si(1≤i≤m)表示第i个候选服务,m表示候选服务集合中服务个数.
定义2.QoS属性为Q={q1,q2,…,qn},其中qj(1≤j≤n)表示第j个QoS属性,n为QoS属性的个数.QC和QU分别表示成本型QoS属性和效益型QoS属性集合,成本型QoS属性值越小越好,效益型QoS属性值越大越好.例如,响应时间是成本型QoS属性,而吞吐量、成功率是效益型QoS属性.

对于可表示为实数离散随机变量形式的QoS属性,本文将该条件形式设定为条件状态.
定义4.用户对成本型QoS属性的需求RC={rc1,rc2,…rcn}.对效益型QoS属性的需求RU={ru1,ru2,…,run}.此外,本文将用户的QoS属性需求作为参照点.

当Web服务QoS的信息量充分大时,经验分布函数以概率1一致收敛于分布函数,所以可用经验分布函数作为Web服务QoS的近似分布函数.因此针对Web服务的QoS不符合特定分布情况,本文用经验分布函数对每个服务的不确定QoS属性进行描述.具体计算公式如下所示:
(1)
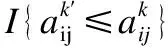
(2)

因此,QoS不确定条件下的服务选择问题描述为:给定QoS信息,比较用户的QoS需求与Web服务QoS信息,利用经验分布函数描述QoS属性的不确定性,根据前景理论得出服务的综合前景值,并以服务的综合前景值选择服务.
4 基于前景理论的服务选择模型
本文运用前景理论建立服务选择模型对Web服务进行选择.前景理论属于心理学及行为科学范畴,为在风险和不确定情况下考虑心理因素对决策影响的问题而提出,是处理不确定性信息的重要工具.
前景理论的核心思想是:首先设定参照点,根据与参照点的比较结果分为收益和损失,然后建立相应的风险矩阵;考虑用户的风险态度,通过价值函数和概率权重函数得出综合前景值,然后对其进行评估与选择.因此,本文是将用户选择服务时的风险态度和服务选择过程有机结合,提出考虑QoS不确定条件下的Web服务选择方法,从用户的需求和风险态度角度出发,量化服务选择过程中的不确定性.
根据前景理论思想,本文首先获取用户对QoS属性的需求作为参照点,将其与Web服务的QoS信息进行比较,得到相较于参照点的收益和损失,并构建相应的风险矩阵(风险收益、损失矩阵);其次用经验分布函数对每个服务的不确定QoS属性进行描述;然后考虑用户的风险态度,根据风险矩阵和QoS属性的分布概率,利用前景理论中的价值函数和概率权重函数计算得出Web服务的综合前景值.最后根据Web服务的综合前景值实现服务排序和选择.
4.1 风险收益和损失计算
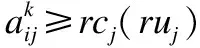
(3)

(4)

(5)

(6)
4.2 服务选择排序
本文中服务选择排序的核心思想是获取每个候选服务的综合前景值,根据综合前景值的大小得出候选服务的排序次序,最终选出最优服务.因此,使用前景理论中的价值函数和概率权重函数计算每个候选服务的综合前景值.
利用价值函数V获得每个服务针对各QoS属性的收益、损失价值.价值函数是用户的主观感受价值[17],其具有以下特征:第一,价值函数是关于决策参照点的变化量的函数,指的是相对于某个参照点的收益或损失;第二,价值函数为S形曲线,即在参照点下方为凸函数,用户面临收益时表现出风险规避态度,在参照点上方为凹函数,用户面临损失时表现出风险偏好态度.
考虑用户对收益、损失价值的风险态度,分别计算每个服务针对各QoS属性的收益、损失的价值V.
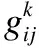
(7)

(8)
式(7)-式(8)中α为风险偏好系数,β为风险规避系数,0<α、β<1,α和β值越大,表示用户对价值的敏感性越弱;λ为损失规避系数,λ>1,λ值越大表示用户对损失越敏感.
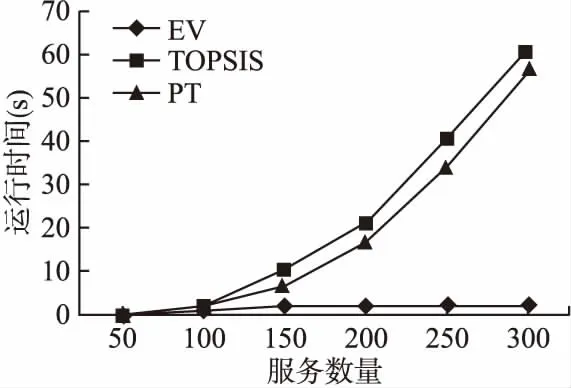
利用概率权重函数π获得每个服务针对各QoS属性在收益、损失情况下分布概率的权重.其具有以下特性:第一,概率权重函数不是客观概率,是将客观概率作为自变量,主观权重作为因变量而建立的映射关系;第二,当分布概率p很小时高估小概率事件,赋予过大权重,有π(p)>p;当分布概率p很大时低估大概率事件,赋予过小权重,有π(p) 考虑用户对待收益、损失的不同风险态度,计算每个服务针对各QoS属性的收益、损失情况下的概率权重. (9) (10) 式(9)-式(10)中γ为风险收益态度系数,δ为风险损失态度系数,0<γ、δ<1,当γ一定时,随着δ的减少,用户会高估小概率事件,对损失赋予的权重更高,即是风险偏好的;当δ一定时,随着γ的减少,则对收益赋予的权重更高,风险态度则为风险规避. 对于参数α、β、λ、γ、δ的取值问题,相关的学者进行了研究得出多种取值情况,本文中的实验默认选用PT方法提出者提供的参数值α=0.88、β=0.88、λ=2.25、γ=0.61、δ=0.69[5]. 根据已得出的收益、损失的价值V(+)和V(-),以及相应的概率权重π(+)和π(-).通过式(11)-式(12)计算得出前景值V并规范化为V*. (11) (12) 最后,依据简单加权原则以及QoS属性权重ω,计算得出综合前景值U,计算公式如下所示. (13) 综上所述,在QoS不确定条件下,基于前景理论的Web服务选择方法步骤如下: 步骤1.根据不确定QoS信息,与参照点对比,根据式(3)-式(6)处理后得到风险收益矩阵G和风险损失矩阵L. 步骤2.根据经验分布函数及式(1)-式(2)对不确定QoS信息进行描述. 步骤3.根据前景理论及式(7)-式(12)计算得出前景值V并规范化为V*. 步骤4.根据式(13),计算得出综合前景值U. 步骤5.根据步骤4得到的综合前景值U大小并对所有的服务进行排序,综合前景值Ui越大,服务si为最优选择. 为验证本文服务选择模型的合理性和有效性,本文实验使用WS-DREAM数据集[18],其包括5825个分布在73个国家的实际Web服务的1974675个事务记录,其中包括响应时间和吞吐量两个QoS属性真实数据.实验环境是CPU为Intel Core i3-4130u,3.4GHz,内存为8GB,操作系统为Windows 10,利用Matlab实现本文方法. 5.1.1 有效性验证 本实验的目的是验证本方法的有效性.我们选择E-V模型(Mean-Variance Model均值-方差)[19]和TOPSIS[20](Technique for Order Preference by Similarity to an Ideal Solution,逼近理想解)方法作为对比方法,通过EMV[21](expected monetary value)、EOL[22](expected opportunity loss)和EUV[23](expected utility value)三个准则进行有效性验证. 我们随机选取50~300个Web服务信息,考虑到用户需求这一因素对服务选择的影响以及QoS属性的表示形式为实数离散随机变量形的情形,在实验中分别以二分位数、四分位数(上四分位数、下四分位数)作为参照点,判断由PT方法选择的最优服务与TOPSIS方法、E-V模型选出的服务是否满足EMV、EOL、EUV三个准则. 在本实验中,参考点变化对Web服务综合前景值的影响如图1所示. 图1 参考点变化对Web服务综合前景值的影响Fig.1 Impact of reference point changes on the comprehensive prospect value of Web services 由图1(a)-图1(c)可分别直观地看出,当参照点取值不变时,随候选服务数量的增加,相较于TOPSIS和E-V模型选择的服务,通过PT方法选择的服务满足EMV、EOL、EUV三个准则的百分比最高;当变化参照点取值时,例如图1(a)所示,保持候选服务数量相同时,相较于E-V模型和TOPSIS方法选择的服务,由PT方法选择的服务满足三个准则的百分比最高. 因此,由图1(a)-图1(c)可以得出:在变化参照点取值的情况下,并随服务数量的增加,相较于TOPSIS和E-V模型选择的服务,通过PT方法选择的服务更满足EMV、EOL、EUV三个准则.说明针对Web服务在QoS不确定下的选择具有风险性这一情况,并且考虑用户需求这一因素,PT方法的选择结果比起E-V模型和TOPSIS方法的选择结果更加有效. 5.1.2 运行效率 在不同样本规模下,记录系统每次进行服务选择的运行时间(单位:s),运行结果如图2所示. 图2 运行时间Fig.2 Response time 当Web服务数量少于50时,PT方法、TOPSIS方法和E-V模型的运行时间并无太大差别.当服务数量超过100时,PT方法与TOPSIS方法的运行时间差距较小;与E-V模型相比,虽然本方法的运行时间较长,但本方法是在不确定QoS条件下考虑用户需求和风险态度两个因素的Web服务选择,所以本方法的选择过程比其他两种方法消耗时间长. 5.1.3 局部服务选择对全局服务选择的影响 本实验的目的是分析由PT方法选出的局部最优服务对全局服务组合的影响.在相同活动数目的情况下,调整每个活动的候选服务数目对组合服务的成功率的影响.以旅游业务集成[24]为例,每一活动分别有10,20,30,40,50个候选服务,每种情况进行20次平均计算,随着候选服务数目的变化,构造服务组合成功率的趋势如图3所示. 图3 候选服务数目对服务组合成功率的影响Fig.3 Influence of number of candidate services on success rate of service composition 图3表明当候选服务数在10~50之间变化时,随着候选服务数的增多,组合成功率变化平稳.并且由PT方法选出的最优服务与TOPSIS方法、E-V模型选出的服务相比,服务组合成功率明显,这表明本文方法选出的局部最优选择对服务组合的求解与其余两种方法相比是有效的. 本实验的目的是分析风险态度参数α、β、λ、γ、δ对服务选择的影响.在QoS不确定条件下的服务选择过程中,若用户需要根据自己的风险态度选取某些候选服务,就可以通过调整α、β、λ、γ、δ的取值,从而改变相应服务的综合前景值及排序,最终选取符合用户选择服务时的风险态度. 依据文献[4,5]和文献[25]提供的参数取值,实验随机选取8个候选服务信息,权重分别设定为0.5、0.5,分别计算参数α、β、λ、γ、δ在不同取值下的综合前景值,经过多次实验取其平均结果,并将结果变化列于图4(a)-图4(e). 图4 参数值变化对Web服务综合前景值的影响Fig.4 Influence of parameter value change on the comprehensive prospect value of Web services 当参数γ、δ取值不变时,将参数α值依次取(0.25,0.54,0.88,0.91)、λ值依次取(0.25,0.54,0.88)、β值依次取(1,1.5,2,2.25,2.5,3,3.5,4,5,6,12)做对比,对比结果如图4(a)-图4(c)所示. 当参数α、β、λ取值不变时,将参数γ值依次取{0.25,0.61,0.74,0.81,0.91}、δ值依次取{0.25,0.69,0.74,0.91}做对比,对比结果如图4(d)-图4(e)所示. 从图4(a)-图4(e)可以看出,随着α、β、λ、γ、δ取值的增大,一方面,各个服务的综合前景值产生明显的变化;另一方面,α、β、γ、δ、λ的取值对候选服务排序有一定的影响,但影响微小,这种影响主要体现在的s1和s3的排序上.当α、β、λ的取值变化导致风险偏好、风险规避程度增强时,s1优于s3;反之,s3优于s1.当δ一定时,随γ值的减少时,对收益赋予的权重会高估小概率事件,用户态度是风险规避;当γ一定时,随δ值的减少时,对损失赋予的权重会高估小概率事件,用户态度是风险偏好.综上,α、β、λ、γ、δ取值的变化不会影响候选服务中最优和最差服务的排序,但会影响中间服务的排序,其综合前景值会随α、β、λ、γ、δ取值的变化明显波动,因此α、β、λ、γ、δ能够显著地体现风险态度因素对于Web服务综合前景值的影响. 本文针对基于不确定QoS的Web服务选择问题,旨在考量用户QoS需求和选择服务时的风险态度对最优服务选择的影响,提出了一种基于前景理论的不确定QoS感知的Web服务选择方法.该方法首先根据Web服务的QoS信息得出用户需求作为参照点,考虑用户风险态度,再通过前景理论得出候选服务的排序并进行选择,为在不确定QoS条件下的Web服务选择提供了一种新的思路.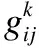

5 实验与分析
5.1 有效性分析
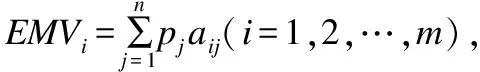


5.2 参数敏感性分析

6 总 结

