大沽河下游农田土壤水分含量动态变化特征①
辛 祥,林 青,黄修东,徐绍辉*
大沽河下游农田土壤水分含量动态变化特征①
辛 祥1,林 青1,黄修东2,徐绍辉1*
(1 青岛大学环境科学与工程学院,山东青岛 266071;2 青岛市水文局,山东青岛 266071)
土壤水分作为土壤的组成部分以及“四水”转化的重要环节,其储存情况严重影响土壤中其他环境因子,因此,研究含水量动态变化特征具有重要的意义。回归等值线图能够较为直接地反映出土壤水分的时空分布。通过田间采样监测,获得了大沽河下游地区6个代表性农田剖面2017年4月21日至12月2日5 ~ 150 cm深度的土壤含水量数据,并采用回归等值线法分析其动态变化特征。结果表明:除研究区中部的毛子埠监测点外,其余5个监测点所求回归方程均能较好再现实际含水量;在时间尺度上,研究区南部、中部及北部沙梁监测点的土壤含水量随时间推移先减少,而后增加,最后再减少;位于研究区最北部的南村监测点,其土壤含水量随时间呈“增加–减少”趋势;在空间尺度上,北部两个监测点存在差异,其中南村监测点随研究深度增加,土壤含水量也逐渐增加;而沙梁与南部监测点相同,土壤含水量随深度先增加后减少;中部六里监测点的土壤含水量随深度先减少后增加。另外,可根据土壤含水量的剖面分布判断零通量面位置,并据此推测水分在空间上的运动方向。土壤含水量的变化随降雨量增加表现出一定的滞后效应,研究区降雨主要集中在7、8月份,除北部的南村监测点外,各监测点各深度土层含水量一般在9月达到最大值。该研究结果可以为合理制定区域土壤水–地下水联合调控方案提供科学依据。
大沽河下游;土壤;含水量;时空变化;回归等值线法
土壤水是大气水、地表水以及地下水相互联系的纽带,是大气降水的主要贮存转换场所,也接受地表水与地下水的部分补给,尤其在地下水位埋藏较浅的区域或季节。土壤水分受降雨入渗、灌溉、蒸发、地下水补给等共同作用,变化复杂[1]。水分在土壤中的储存、运动和变化对土壤环境有着很大的影响[2],土壤水影响着水资源的开发利用、生态环境保护和渗流带污染物迁移的预测[3]。土壤水分具有时间和空间异质性[4-10],了解土壤水分在不同时空尺度上的动态特征对其他诸多生态过程和水文过程研究至关重要[11-13]。国内外学者开展了许多土壤含水量变化及影响因素的研究。Kondo等[14]利用水、热平衡原理分析得出,在半干旱地区,土壤含水量的年平均值随着深度、年降水量的增加而增加;Wang等[15]利用回归统计方法得出,气候变化对土壤水分的影响主要集中在夏秋季节,且达到显著水平;Yao等[16]研究发现土地利用方式是土壤水分空间异质性的主导因素;韦佳等[17]发现土壤水分的变化综合地反映了土地利用变化与气候变化的影响;此外,周乃健等[18]提出了研究土壤水分变化特征的新思路,认为土壤水分的时空(某个时段,某种深度范围)变化是一个连续的过程(相当于产生了图形中的“面”),并且将时间等值线法与回归法结合为回归等值线法,在土壤水分时空变化动态分析中取得了理想的效果。
回归等值线法能够反映土壤水分时空动态变化的基本趋势和特征,具有简单省时、图形简洁明了、信息量大、便于分析等特点,可以用于土壤水分测定数据的整理和分析[19],并且可以清晰地概括出某一时间段土壤水分从表层到深层的湿度变化过程及特征,同时还能在一定程度上反映地表蒸散、降水以及地下水补给状况[20]。
大沽河地区农业用水主要以开采地下水为主,20世纪七、八十年代大沽河下游(近胶州湾地区)由于地下水连续多年超采,出现了严重的海水入侵现象。为了探讨地下水、土壤水的联合调控策略,有效配置水资源,杨玉峥等[21]曾对大沽河中游地区土壤水与浅层地下水转化关系进行了研究,而大沽河下游及海水入侵区的土壤水分含量在时空上如何变化,有待深入分析,这对土壤水-地下水联合管理及调控,更加合理地开采地下水,防止海水入侵区咸水向内地的进一步扩展具有重要意义。本文利用回归等值线法,对大沽河下游农田从小麦返青期到土壤冻结期这一时间段内的土壤水分含量动态变化特征进行了研究。
1 材料与方法
1.1 研究区概况
大沽河是山东半岛主要河流之一。研究区位于山东省青岛市大沽河下游(近胶州湾)平原地区,北起平度市南村镇,南抵修建地下截渗墙的大麻湾,地理位置120°00′ ~ 120°18′ E,36°18′ ~ 36°34′ N,面积约700 km2(图1)。大沽河流域属于华北暖温带沿海湿润季风区,受海洋环境影响和调节影响明显,雨热同期,多年平均降雨量675.6 mm[22],降水主要集中在6—9月,约占全年的69.2%,多年平均气温12.2℃,多年平均蒸发量983.8 mm,是平均降水量的1.45倍。
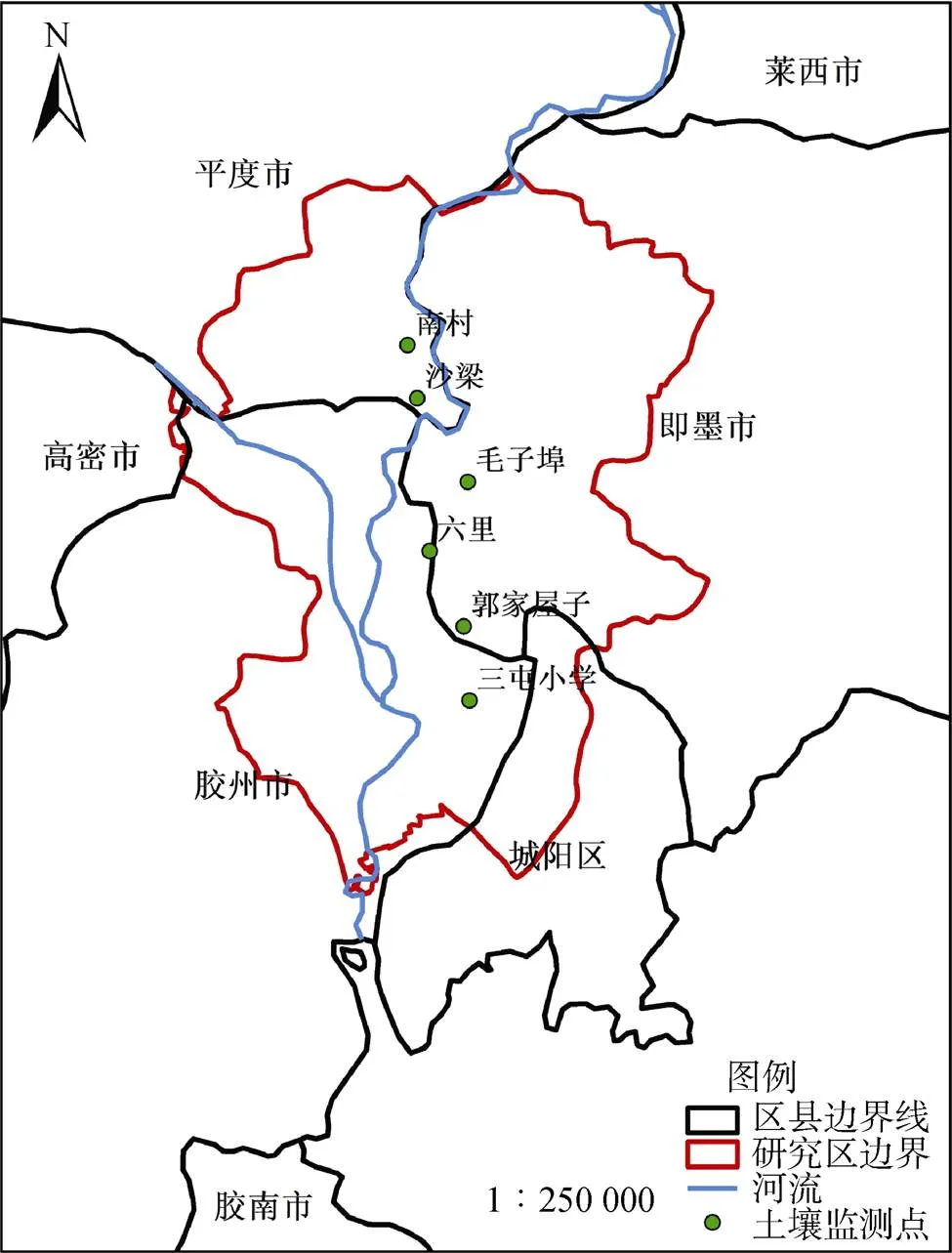
图1 研究区及监测点分布图
1.2 土壤含水量监测
本研究试验时间为2017年4月21日至2017年12月2日,历时225d。在研究区范围内的农田选取6个代表性监测点进行土壤含水量的监测,监测点信息如表1所示。监测点大致均匀布置在下伏有地下水的区域,各监测点的土地利用类型均为耕地,并且农作物均为冬小麦-夏玉米轮作,分别在6个不同的深度5、20、40、70、100和150 cm处用土钻采样进行土壤含水量的测定。一般每10 天取样1次,雨后需加密1次,共计取样18次。试验同时测定土壤的粒径组成、容重、阳离子交换量(CEC)、pH。土壤的粒径组成采用筛分法测定,依据美国农部制土壤质地三角形对各监测点的土壤进行质地分类;土壤容重采用环刀法测定;土壤含水量采用烘干法进行分析[2],计算得到体积含水量;采用乙酸铵交换法测定土壤CEC;采用蒸馏水浸提测定土壤pH。
1.3 数据处理与分析
所有调查数据采用Excel、SPSS19.0进行数据处理和分析,利用MATLAB实现回归等值线图的绘制,利用Origin9.0绘制观测值的散点与计算值的比较图。本研究以首次测定时间(2017年4月21日)为第0 天,至2017年12月2日为第225 天。
含水量除用体积分数表示外,还可用贮水深度(一定厚度土层中,所含水量折算成的水层深度)表示[23]。本研究采用周乃健等[18]提出的回归等值线法,将不同时间不同深度的土壤含水量(cm3/cm3)转化为0 ~ 20 cm土层水分深度(mm),以取样深度(1,cm)和监测时间(2,d)为自变量,以水层深度(mm)为因变量,利用回归方法求出每一个地点的包括一次交互项的二元二次、三次方程。根据复相关系数值随着方程幂次增加而增加的幅度大小以及由回归方程所得值绘制出的土壤水分等值线图的代表性,为各个地点每个深度选择合适的回归方程,再依据回归方程,利用MATLAB绘制出土壤水分时空动态分布图。因中部的毛子埠监测点所求回归方程不能反映实际含水量及变化趋势,故此次仅利用回归等值线图法分析其余5个监测点的土壤含水量动态变化特征。
2 结果与分析
2.1 土壤粒径及土壤含水量描述性统计
土壤颗粒组成决定了不同土层的持水性能,颗粒组成不同是导致土壤水分分布及运动方式发生变化和影响水分在土壤中去留的根本原因[24]。5个监测点各个深度土层的粒径组成、容重、质地等信息如表2所示。
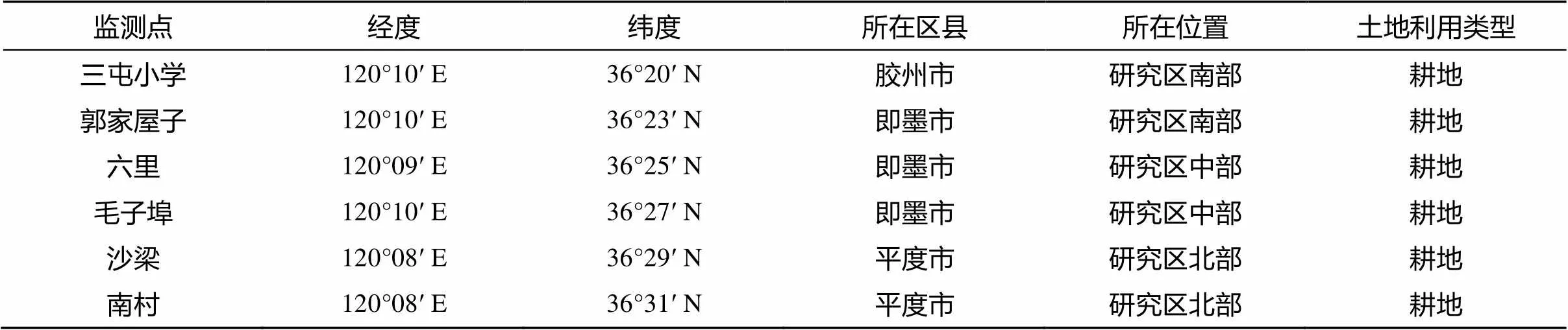
表1 监测点位置及土地利用类型

表2 监测点土壤粒径组成、CEC、容重及pH
表3为土壤含水量在18个测次上的平均值、标准差、变异系数等的描述性统计。根据郝振纯等[25]的研究,变异系数CV≤0.1时为弱变异,0.1<CV<1.0为中等变异。由表3可以看出,随着时间变化,除了南部的监测点三屯小学深度为70 cm和100 cm以及郭家屋子深度为40 cm和100 cm的土壤含水量CV<0.1,属于弱变异,其余监测点各个深度的CV均在0.1 ~ 1.0,一般<0.3,属于中等强度的变异,这就表明土壤含水量随时间推移变化并不显著。由于受到蒸发作用、大气降水的影响,表层(5 cm)的CV最大,土壤水分活跃程度最高;并且地下水埋深较浅,补给作用明显,深层(150 cm)的CV较大。20 ~ 100 cm的CV为0.10 ~ 0.27,土壤水分含量比较稳定,说明除较强降雨外,这个深度范围一般不会受到降水以及地下水的影响。由于研究区范围较大,降雨、土壤质地以及地形等因素差异较大,无法考虑到各个监测点之间在空间上的变异性,因此采用回归等值线法仅观察每个监测点土壤水分时空分布特征。
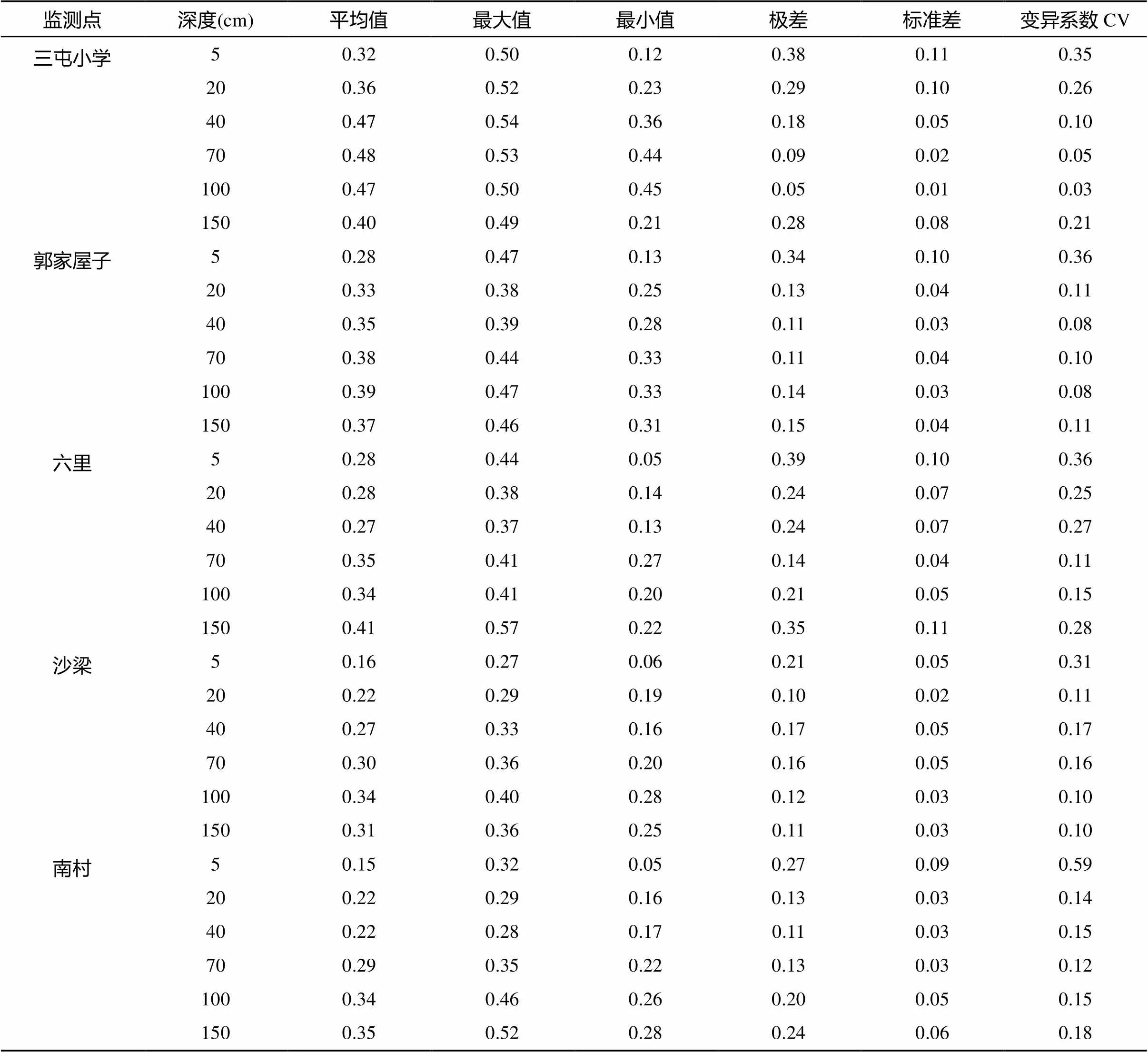
表3 不同监测点不同深度土层土壤含水量描述性统计(cm3/cm3)
2.2 土壤含水量回归方程的建立
利用回归法求得不同监测点剖面土壤水分时空分布的二次、三次回归方程,为兼顾5个地点及回归方程的一致性,本研究此次选择二元三次回归方程,5个监测点所求回归方程为:三屯小学:=52.52 +1.2841–0.309 42–0.011 9812+ 0.005 04022+ 0.000 029 1713–0.000 016 7423+ 0.000 109 512,= 0.719,=15.258;郭家屋子:=58.35 + 0.53711– 0.157 42–0.004 28312+ 0.002 26022+ 0.000 009 14713– 0.000 008 39723+ 0.000 177 912,=0.590,=7.633;六里:=51.74 – 0.127 81– 0.291 72+ 0.003 51112+ 0.005 70822– 0.000 013 1913– 0.000 021 4723+ 0.000 695 912,=0.696,=13.454;沙梁:=35.96 + 0.825 51– 0.300 32– 0.005 80612+ 0.003 34922+ 0.000 011 9713– 0.000 010 5623– 0.000 005 41312,=0.845,=35.547;南村:=31.21 + 0.412 51+ 0.143 02– 0.000 273 112– 0.001 32922–0.000 006 49913+ 0.000 001 76123+ 0.000 449 712,=0.820,=29.216。查值临界表可知,0.01的值约为2.66,5个监测点回归方程的值均大于2.66,达到0.01的显著水平,说明每个回归方程都能很好地表示相应监测点的土壤水分时空分布特点。将各个深度(1,cm)与时间(2,d)带入回归方程求出计算值,与观测值比较,可分析回归等值线法的准确性。图2为土壤含水量根据回归方程的计算值与实测值的比较。可见,计算值能较好地代表着观测值,所以根据回归方程计算值绘制含水量等值线图,用等值线图分析土壤剖面含水量动态变化特征,回归方程的常数项表示该点2017年4月21日(2=0),表层(1=0)的土壤水分含量(mm)。
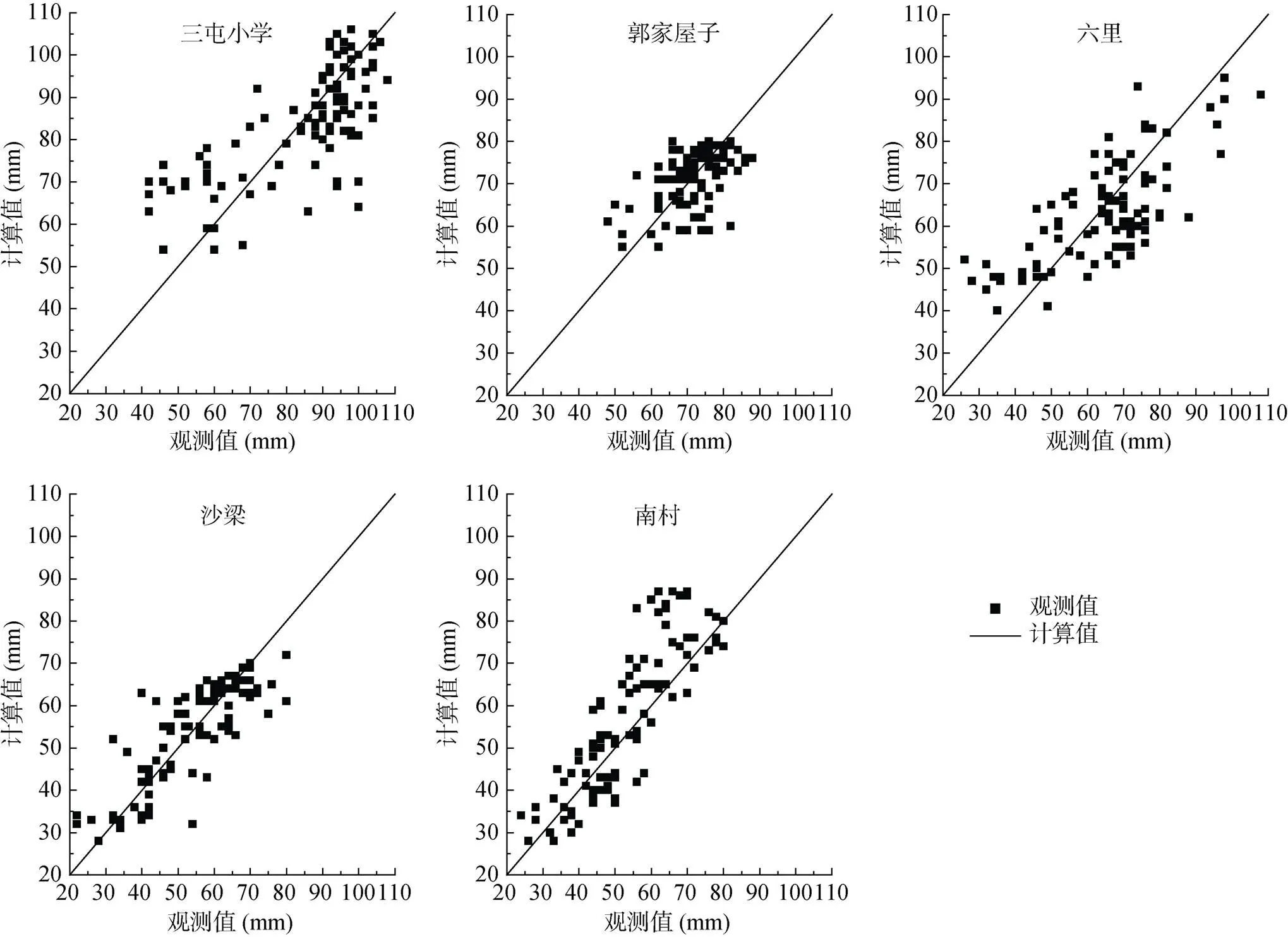
图2 监测点水分含量的观测值与计算值
2.3 土壤含水量变化特征
根据回归方程计算出每个深度(1,cm)和每个时间(2,d)对应的水分含量(mm),绘制土壤水分含量时空变化图(图3)。由图3可见,5个监测点的回归等值线图上部的等值线分布较为密集,说明表层由于受到降水、蒸发等影响,水分含量变化强烈,这与表3中变异程度所表达的土壤水分的活跃程度相符。回归等值线图的形状取决于回归方程的系数以及系数的正负[19]。从图3中回归等值线图的形状可以看出,研究区南部的两个监测点(三屯小学和郭家屋子)与北部的沙梁监测点的回归等值线图具有一定的相似性,其土壤含水量随着时间推移先减少,而后增加,最后再减少,存在最大值与最小值;在垂直方向上,随土壤深度增加,土壤含水量先增加后减少,且存在一个密闭的水分含量高值区域。观察各监测点的回归方程发现,这3个监测点的回归方程除一次交互项的系数外,其余各项系数的正负均一致,并且各项系数的绝对值的大小也具有相同的顺序关系。中部监测点(六里)的土壤含水量随时间推移的变化趋势与上述3点一致,但是随土壤深度增加,含水量先减少后增加。位于研究区北部的南村监测点的土壤含水量变化特征与同样位于北部的沙梁监测点表现出一定的差异,其土壤含水量随深度增加也逐渐增加,但随时间的推移呈现“增加–减少”的变化。
从图3还可以看出,研究区南部的三屯小学监测点和郭家屋子监测点与北部沙梁监测点土壤含水量虽然具有类似的时空分布规律,但含水量达到峰值的时间与深度存在差异。三屯小学监测点各个深度的土壤水分含量在第40天(5月31日)达到最低,在第160 天(9月28日)达到最高;在垂直方向上,在深度约为70 cm处,土壤含水量达到最高。郭家屋子监测点的土壤含水量也在约第40 天(5月31日)达到最低,但在第140天(9月8日)达到最高,并且在深度为100 cm处土壤水分含量最高。北部沙梁监测点在第60 天(6月20日)时达到最低,在第140 天(9月8日)达到最高,深度为100 cm处最高。另外,中部的六里监测点在40 cm处含水量最低;北部的南村监测点在第80 天(7月10日)最高。不同监测点同一时间同一深度土壤含水量差别较大,说明含水量在研究区内空间变异性大。
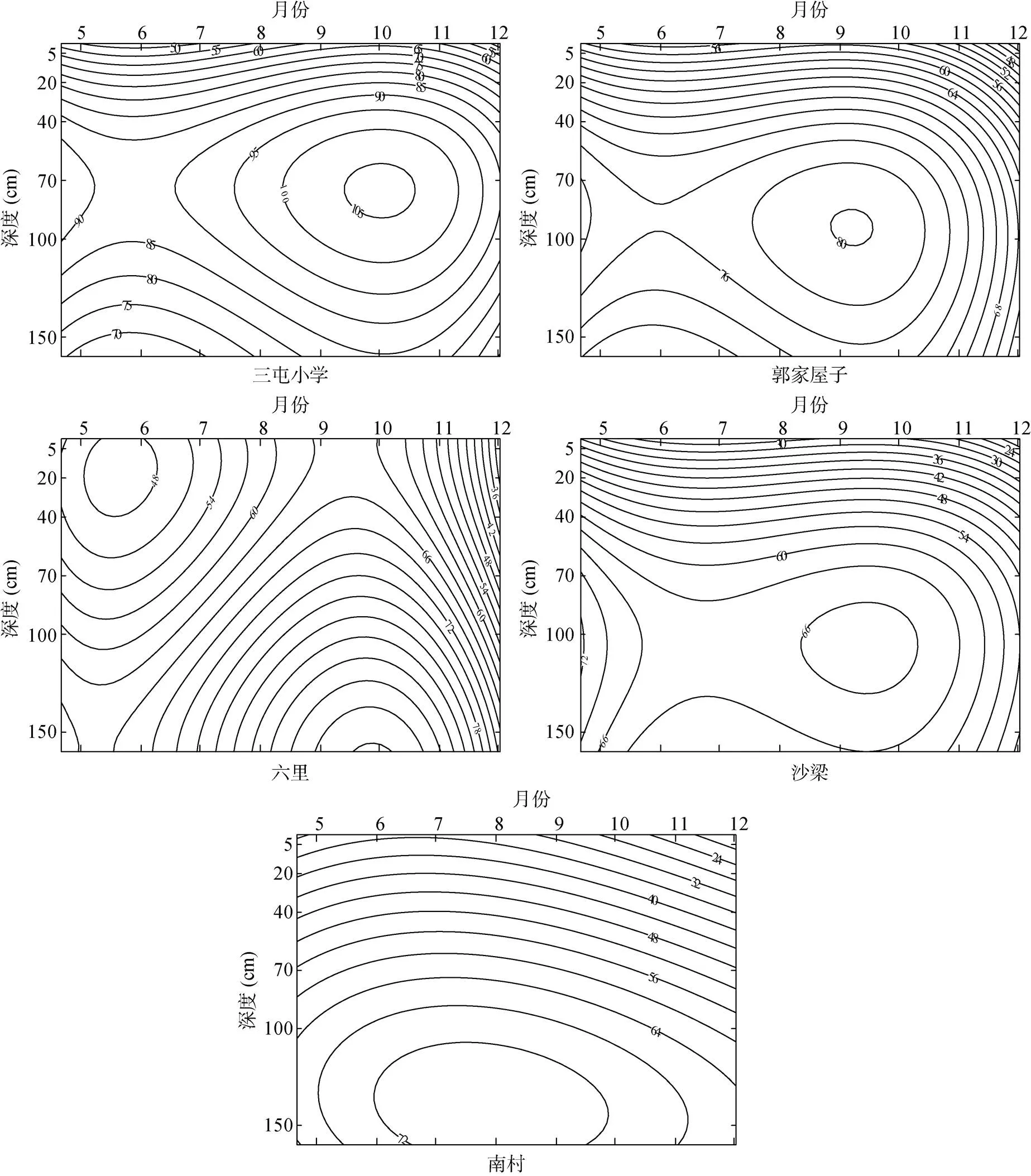
图3 监测点土壤水分含量(mm)的回归等值线图
图4为从青岛水利部门收集的监测点所在区县2017年3—11月的降水信息,研究区降水主要集中在7、8月份,但除南村监测点外,各监测点土壤含水量的最高值一般出现在9月,可见,土壤含水量的变化随降雨量的增加表现出一定的滞后性。7、8月份的集中性降雨使得水分向更深层移动,从而使得各个深度的土壤含水量在9月份达到峰值,继而随着降雨量的减少、地表蒸发以及下层水分向更深处移动补给地下水,所观察的各个深度土壤含水量呈现递减的趋势。另外,不同深度土壤含水量对降雨的响应一致,这与周刘宗等[26]的研究结果不同。

图4 2017年胶州市、即墨市、平度市降水量
研究区南部三屯小学和郭家屋子监测点及位于北部的沙梁监测点分别在约70、100、100 cm深度土壤含量达到峰值,土壤水吸力在3个深度最小。根据土壤含水量的剖面分布可判断零通量面位置,并据此推测土壤水分在空间上的运动方向。由此,在此3个深度之上由于蒸发作用,水分自下而上运动;下部土壤水分处于继续向下入渗状态,形成发散型零通量面。
位于研究区南部的监测点土壤含水量变化具有相同的特征,而位于研究区北部的两个监测点表现出差异,这是由于研究区范围较大,土壤质地等因素存在差异导致的。因此,需要更多的监测点来研究区域内不同监测点之间的含水量空间变异性,此次结果可为接下来的研究提供参考。
2.4 土壤含水量回归方程计算值与观测值的趋势比较
本文以北部南村监测点20 cm深度和沙梁监测点20 cm深度(图5)为例,分析土壤含水量观测值与计算值随时间变化的趋势,从图5中可以看出,观测值与计算值随时间推移呈现相同的变化,但计算值与观测值存在一定差异,如从南村监测点20 cm深度图看,回归方程计算值约小于观测值5 mm(即体积含水量2.5 cm3/cm3)。以沙梁监测点第25天和郭家屋子监测点第169天(图6)为例,分析研究区南部与北部土壤含水量随土壤深度的变化,从图6中可以看出,计算值与观测值的变化趋势一致,而且北部监测点计算值与观测值的对应性较好,南部监测点虽存在误差,但误差较小。可见,计算值趋势线可以很好地表现出土壤含水量的变化。
因此,本研究所选回归方程和回归等值线图基本能够描述和反映不同监测点土壤水分时空变化的总体特征和趋势。土壤水分时空分布回归等值线法特别适用于土层深厚、剖面土层性质尤其是质地比较一致的土壤。在时间上,该法更适合于反映较长时间内的土壤水分动态变化,突出土壤水分时空变化的内在规律。
3 结论
1)除研究区中部的毛子埠监测点外,其余5个监测点所求回归方程均能较好反映土壤含水量随时间及深度的变化特征。回归等值线法在分析大沽河下游农田土壤水分分布特征及运动趋势方面得到了很好的应用,回归方程计算值与观测值相比,虽存在一定误差,但可较好地反映含水量的变化趋势。
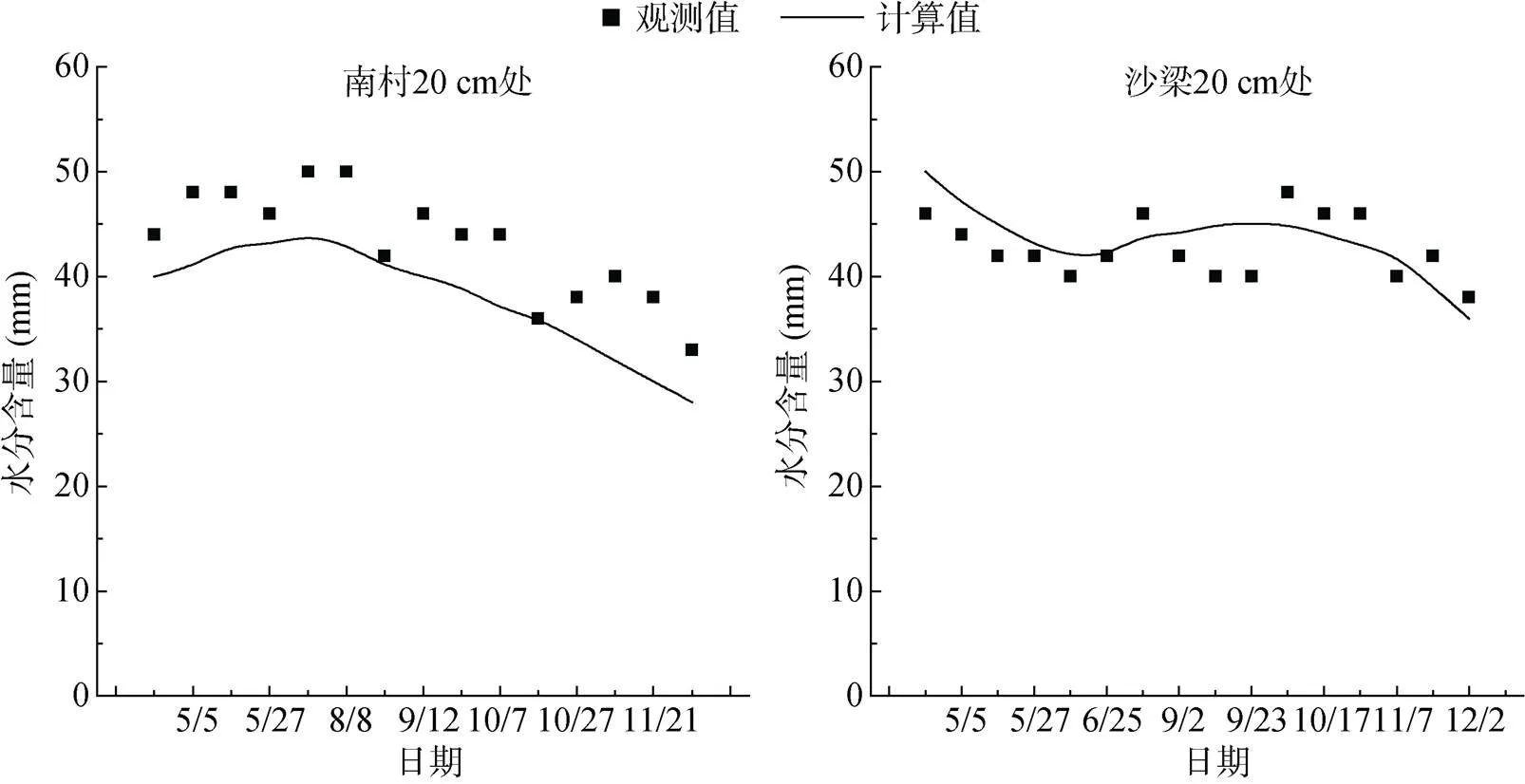
图5 土壤水分含量随时间变化的观测值与计算值

图6 土壤水分含量随土壤深度变化的观测值与计算值
2)在研究时段内,研究区南部和中部的监测点及位于北部的沙梁监测点的土壤含水量随时间推移先减少,而后增加,最后再减少;位于研究区最北部的南村监测点,其土壤含水量随时间呈“增加–减少”趋势。在研究的土壤深度内(5 ~ 150 cm),北部两个监测点土壤含水量存在差异,其中南村监测点随土壤深度增加,土壤含水量也逐渐增加;而沙梁监测点与南部监测点相同,土壤含水量随土壤深度先增加后减少;中部监测点的土壤含水量随土壤深度先减少后增加。造成这种差异的原因主要为地下水埋深、降雨量以及土壤质地的差异。
3)研究区南部的两个监测点及北部的沙梁监测点的土壤含水量分别在深度为70、100、100 cm时达到最大值。在此3个深度之上由于蒸发作用,水分自下而上运动;下部土壤水分处于继续向下入渗状态,形成发散型零通量面。
4)土壤含水量的变化随降雨量的增加表现出一定的滞后性,研究区降雨主要集中在7、8月份,除研究区北部的南村监测点外,各监测点各深度土层含水量一般在9月达到最大值。
5)由于研究区范围较大,监测点较少,本研究不能分析不同监测点之间的空间变异性;而且由于缺乏地下水水位数据,本研究不能量化由地下水位变化导致的150 cm含水量变化。
[1] 靳宇蓉, 鲁克新, 李鹏, 等. 基于稳定同位素的土壤水分运动特征[J]. 土壤学报, 2015, 52(4): 792–801
[2] 邵明安, 王全九, 黄明斌. 土壤物理学[M]. 北京: 高等教育出版社, 2006: 47–60
[3] 王金生, 杨志峰, 陈家军, 等. 包气带土壤水分滞留特征研究[J]. 水利学报, 2000, 31(2): 1–7
[4] Mohanty B P, Famiglietti J S, Skaggs T H. Evolution of soil moisture spatial structure in a mixed vegetation pixel during the Southern Great Plains 1997(SGP97) hydrology experiment[J]. Water Resources Research, 2000, 36(12): 3675–3686
[5] Vachaud G, Silans A P D, Balabanis P, et al. Temporal stability of spatially measured soil water probability density function[J]. Soil Science Society of America Journal, 1985, 49(4): 822–828
[6] José M, Antonio C. Temporal stability of soil moisture in a large-field experiment in Spain[J]. Soil Science Society of America Journal, 2003, 67(6): 1647–1656
[7] Kachanoski R G, Jong E. Scale dependence and the temporal persistence of spatial patterns of soil water storage[J]. Water Resources Research, 1988, 24(1): 85–91
[8] 米合热古丽·塔什卜拉提, 塔西甫拉提·特依拜, 买买提·沙吾提, 等. 于田绿洲盐渍土水、盐、温度季节变化规律与相关性研究[J]. 土壤, 2018, 50(1): 162–172
[9] Brocca L, Morbidelli R, Melone F, et al. Soil moisture spatial variability in experimental areas of central Italy[J]. Journal of Hydrology, 2007, 333(2): 356–373
[10] 翁倩, 袁大刚, 张楚, 等. 四川省土壤水分状况空间分布特征[J]. 土壤, 2017, 49(6): 1254-1261
[11] Ridolfi L, D’Odorico P, Porporato A, et al. Stochastic soil moisture dynamics along a hillslope[J]. Journal of Hydrology, 2003, 272(1/2/3/4): 264–275
[12] Milly P C D, Dunne K A. Sensitivity of the global water cycle to the water-holding capacity of land[J]. Journal of Climate, 1993, 7(4): 506–526
[13] Brubaker K L, Entekhabi D. Analysis of feedback mechanisms in land-atmosphere interaction[J]. Water Resources Research, 1996, 32(5): 1343–1357
[14] Kondo J, Xu J Q. Seasonal variations in the heat and water balances for nonvegetated surface[J]. Journal of Applied Meteorology, 1995, 36(36): 1676–1695
[15] Wang Y P, Meng J, Song W S, et al. Analysis on the relationship between soil moisture and climate change in Hulunbeier City[J]. Research of Soil and Water Conservation, 2009, 16(4): 255–258
[16] Yao X L, Fu B J, Lü Y H, et al. The multi-scale spatial variance of soil moisture in the semi-arid Loess Plateau of China[J]. Journal of Soils and Sediments, 2012, 12(5): 694–703
[17] 韦佳, 蒋名亮, 郭建青, 等. 栾城农田土壤含水量时间统计特性的初步分析[J]. 节水灌溉, 2014(5): 1–3, 6
[18] 周乃健, 王志亚, 郝久青. 回归等值线图在土壤水分时空变化动态分析中的应用[J]. 农业工程学报, 1997, 13(1): 112–115
[19] 卜玉山, 苗果园, 周乃健, 等. 秸秆与地膜覆盖玉米农田土壤水分时空动态变化——兼评回归等值线法的应用[J]. 土壤学报, 2004, 41(5): 795–802
[20] 郝科栋, 郝建平, 杜天庆, 等. 回归等值线图在分析旱地蔬菜全生育期土壤水分动态变化规律中的应用[J]. 山西农业大学学报(自然科学版), 2014, 34(6): 488–493
[21] 杨玉峥, 林青, 王松禄, 等. 大沽河中游地区土壤水与浅层地下水转化关系研究[J]. 土壤学报, 2015, 52(3): 547–557
[22] 刘占良, 赫旭, 安文超, 等. 大沽河流域农田径流污染研究[J]. 中国海洋大学学报(自然科学版), 2009, 39(6): 1305–1310
[23] 雷志栋, 杨诗秀, 谢森传. 土壤水动力学[M]. 北京: 清华大学出版社, 1988: 51–55
[24] 李王成, 冯绍元, 康绍忠, 等. 石羊河中游荒漠绿洲区土壤水分的分布特征[J]. 水土保持学报, 2007, 21(3): 138–143, 157
[25] 郝振纯, 吕美霞, 吕美朝, 等. 坡度作用下土壤水分时空异质性研究[J]. 水文, 2012, 32(2): 5–10, 48
[26] 周刘宗, 陈志雄, 周凌云, 等. 土壤水分的时序分析研究[J]. 土壤, 1998, 30(4): 188–193
Dynamic Characteristics of Soil Moisture in Downstream Farmland of Dagu River
XIN Xiang1, LIN Qing1, HUANG Xiudong2, XU Shaohui1*
(1 College of Environmental Science and Engineering, Qingdao University, Qingdao, Shandong 266071, China; 2 Hydrology Bureau of Qingdao City, Qingdao, Shandong 266071, China)
Soil water is an integral part of soil and an important part of “four-water” transformation. Water storage affects other environmental factors in the soil, so studying its dynamic characteristics is of paramount importance. The regression isogram can reflect the spatio-temporal distribution of water more directly. Through sampling and monitoring in the field, soil moistures of 6 representative farmland sections with depth from 5 cm to 150 cm had been obtained in the downstream area of Dagu River from April 21 to December 2 in 2017 and their dynamic changes were analyzed by regression isogram. The results showed that except for Maozibu point in the middle part of study area, the regression equations obtained in the other five monitoring points could reflect well the actual soil moistures. On the temporal scale, soil moistures of points in southern and central parts and Shaliang point in the northern part of study area decreased first, then increased, and decreased finally with time, while soil moisture in Nancun point in the northernmost part increased first then decreased with time. On the spatial scale, there were differences between the two monitoring points in the north part, as the depth increasing, soil moisture in Nancun point also increased gradually, but that of Shaliang point was consistent with the monitoring points in the southern part, increased first then decreased. Soil moisture in Liuli point in the middle part decreased first then increased. In addition, according to the section distribution of soil moisture, the position of the zero flux plane could be judged and the spatial movement direction of water could be inferred. The change of soil moisture showed a certain lag effect with the increase of precipitation. Because the rainfall mainly concentrated in July and August, except Nancun point in the northern part of the study area, soil moisture in each deep layer in other points reached a maximum in September. The above results can provide references for the proposing the reasonable regional joint regulation program of soil water and groundwater.
Downstream area of Dagu River; Soil; Moisture content; Spatio-temporal change; Regression isogram
国家重点研发计划项目(2016YFC0402807)和国家自然科学基金项目(41571214)资助。
(shhxu@qdu.edu.cn)
辛祥(1992—),男,山东淄博人,硕士研究生,主要从事地下环境中水和溶质运移的数值模拟。E-mail:reebokjones@163.com
10.13758/j.cnki.tr.2019.02.025
S152.7
A

