数字逻辑课程的课堂教学收官
邝继顺
(湖南大学 信息科学与工程学院,湖南 长沙 410082)
0 引 言
课堂(特指在教室里上课)至今仍是教学的主战场,期末考试是课堂教学的最后一个环节,而且是不可忽视的重要环节,主要包括编制试卷、阅卷和试卷成绩分析3个阶段。过去,研究型大学的教师们大都忙于科研,较少顾及教学,出试卷远不如撰写项目申请书下工夫,试卷成绩分析更像做填空题,填几个数字,写几句套话就完事。这种现象长期存在,严重影响教学质量。
1 把学科方法作为重要考点
我国著名教育家陶行知指出,“活的人才教育,不是灌输知识,而是将开发文化宝库的钥匙,尽我们知道的交给学生”[1]。掌握了方法,教育之收效能事半功倍[2]。有学者提出,教育改革应该包括教学方法、教材与教育理论3个方面,并认为大学学科教育的本质是学科方法论教育[3]。
长期以来,课程考试多半考的是概念、原理、按公式计算等知识,再加上一些简单的应用,极少涉及学科方法。因此,学生只关心如何得到正确的结果,不考虑所用方法是否合理、高效。为了强调方法的重要性,在课程考试中进行相关学科方法的测验十分必要。
数字逻辑是笔者承担的一门专业基础课程,教学大纲要求学生理解并在今后的相关实际工作中运用大问题的复杂性、概念和形式模型、抽象层次、重用和折中与决策5个重要概念,逐步从单纯的逻辑思维习惯中解放出来,加强发散思维、经验思维和创造思维多种思维能力的训练,学会使用“理论—抽象—设计”3个过程,解决本学科的复杂工程技术问题。为满足这些要求,笔者编制了如下一份试卷。
第一题 简答题(10分):考查综合概括、文字表达能力、思维与工作作风。
第二题 求简化的真值表(10分):考查抽象表达、处理复杂问题的能力。
第三题 分层设计(15分):考查运用分层思想解决复杂问题的能力。
第四题 时序电路分析(15分):考查分析时序电路的基本方法,画时序图,强调时序的重要性。
第五题 做状态图和状态表(15分):考查状态机的基本概念,如何通过抽象得到状态图。
第六题 HDL程序设计(15分):考查时序电路3进程描述方法,HDL程序设计能力。
第七题 PLA器件应用(10分):考查PLA器件的原理、特点及在受限条件下解决问题的能力。
第八题 双向移位寄存器设计(15分):考查寄存器传输设计思想,综合运用所学知识的能力。
2 合理选择题型
使用什么样的题型是教师编制试卷时考虑的第一个问题,然后分析考哪些知识点,最后再决定用什么题型来考查这些知识点。在不少教师眼里,选择题、填空题、判断题、匹配题和简答题都是用来送分的。为了保证足够的及格人数,这些题型不能少。因此,学生考试前只关心两件事:一是哪些章节要考,二是考什么题型。这种考试心理定式严重影响考试应该发挥的积极作用。
填空题、简答题、政论题和作文题来源于古代的帖文、墨义、策问和诗赋[4]。题型不同,用处不一样,例如帖文用来考记忆,墨义用来考对书中观点的理解。20世纪30年代,由美国倡导的客观试题开始风靡世界,如选择题、判断题、匹配题、完型填空题、排序题被大量使用。客观试题显示出客观、公正,但仅仅指评分时的客观。客观试题无法阻止考生的猜题行为,考生最后获得的成绩并不客观。此外,客观试题还难以考查学生的能力、情感、态度和兴趣等[4]。因此,合理选择题型十分重要。
3 发现隐藏在分数背后的秘密
考试仍然是评定教学效果的一种重要手段。在工程教育专业认证过程中,考试成绩分析还是课程教学达成度计算及其持续改进的依据。
3.1 分析假设
由于课程考试属于合格性测验[5-6],学生分数应该呈现负偏态分布或右移了的正态分布。但基于负偏态分布进行计算存在困难,因此基于正态分布进行计算与分析,同时考虑负偏态分布的特点。
按正态分布考虑,认定平均分数是75分(按百分制计算),分数在60~90分的学生比例为70%,60分以下和90分以上学生的比例各为15%。使用一倍标准差来度量分数分布比较合适,因为一倍标准差以内事件出现的概率为68.3%,与70%比较接近。因此,把理想状态时的标准差定为15分,其相对值为15/75=0.2。
3.2 得分统计与规一化处理
根据不同的分析粒度,分别计算出全体学生、各个小班学生总成绩和每个题目得分的平均值和标准差。以下各表中,“实得分”是学生得分的平均值;“规一得分”是将“应得分”规一到100分时,“实得分”的对应值;“绝对标准差”是学生实际得分的统计标准差;“相对标准差”是“绝对标准差”/“实得分”。
3.3 整体情况分析
将全部学生的成绩放在一起进行统计分析,可以发现教学的总体状态,例如教学内容是否受学生欢迎,使用的教学方法、教学手段是否合理,上课时教师是否存在错误,试卷难度是否适中,考题是否有问题,并为今后改进提供参考。
由于有期中考试,期末考试侧重于时序电路部分。试卷完全去除了填空题、选择题和判断改错题,增加了应用题和主观题的分量,还新增了第七章的内容。因此,由于出题形式发生改变,内容和难度有所增加,学生可能平均少得10分左右。表1是全体学生成绩区间分布表。从表中可以看出,学生成绩呈明显的正偏态分布,不及格的人数太多。
表2是全年级大班(包括4个行政小班)各题得分统计表,其中序号表示“难度”,序号越大则难度越大。
从表2观察到,除第七题得分符合标准的正态分布外,其他各题得分均呈正偏态或左移的正态分布,最终导致总分呈正偏态分布。第八题得分很低,而且标准差很大,一定存在某种特殊原因。仅从表2来看,试题明显偏难。
3.4 个别题特别分析
阅卷时发现第六题有1个班得分很高,其他班得分很低,得分情况见表4—表7的对应项。4班得分90.33分(规一化得分,下同),标准差为0.24(相对标准差,下同),说明难度较低,且绝大多数学生成绩优秀。但是2班和3班得分很低,标准差很大,其中2班表现更为突出,分数呈明显的正偏态分布。综合分析可能有如下原因。
(1)题目不难,只要能够脱离书本进行编程就可以获得较高分数;
(2)除去此题,4班的总分平均值与另外3个班相比多7.3分(见表3),说明4班此题获高分有其合理性;
(3)其他3个班得分较低,而且标准差很大,说明学生们平时做实验大多数照着书本的模板来做的,一旦脱离书本就不知所措。
对于此题,笔者得到的结论是:要加强编程训练,增加编程的频度,并适当加大试题的难度。
将第六题从4个班的成绩中删除后,再根据“规一得分”从高到低对各个题目的难易程度按班级进行重新排序,得到表3。
观察表3发现,对于2、3、4班,除去第六题后,题目难易程度的排序完全一样。对于1班,只要将相邻的第五题和第一题交换位置,相邻的第四题和第二题交换位置,则题目难易程度的排序与其他3个班也完全一样。这说明除去第六题后,其他各题的难易程度对全体学生来说是相同的,存在的问题也应该相同。
3.5 班级差异分析
将各班成绩进行单独分析与相互比较,可以发现班与班之间或许存在某种差异,例如各班的学习风气、班干部或学习标兵所起的作用,这些问题在对大班整体情况进行分析时可能被淹没或不那么明显。表4—表7是各班各题得分统计表。
去除第六题后,1班—4班的总分见表3,其中前3个班的成绩分别是46.58、45.82和47.50,它们非常靠近,但4班成绩是53.94,明显高不少。据此把全部学生分为两类,前3个班合为第一类,4班单独为第二类。表8为第一类学生的成绩统计情况。

表1 成绩分布表

表2 全年级各题得分

表3 去除第六题后各班各题难度排序及总分

表4 1班各题得分
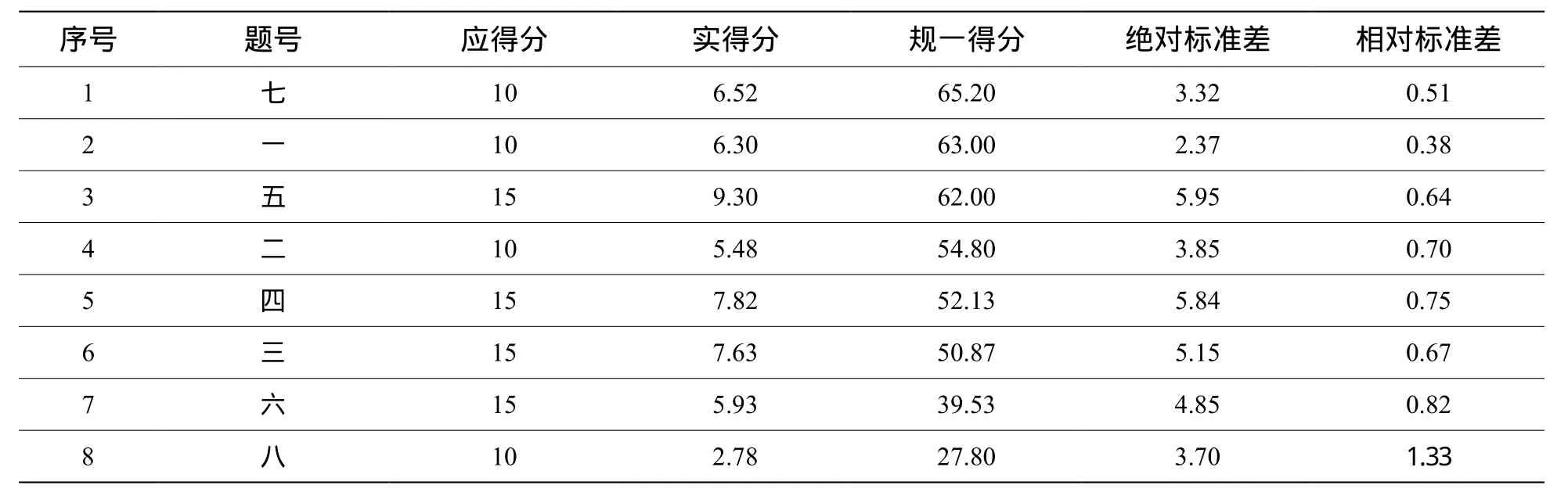
表5 2班各题得分
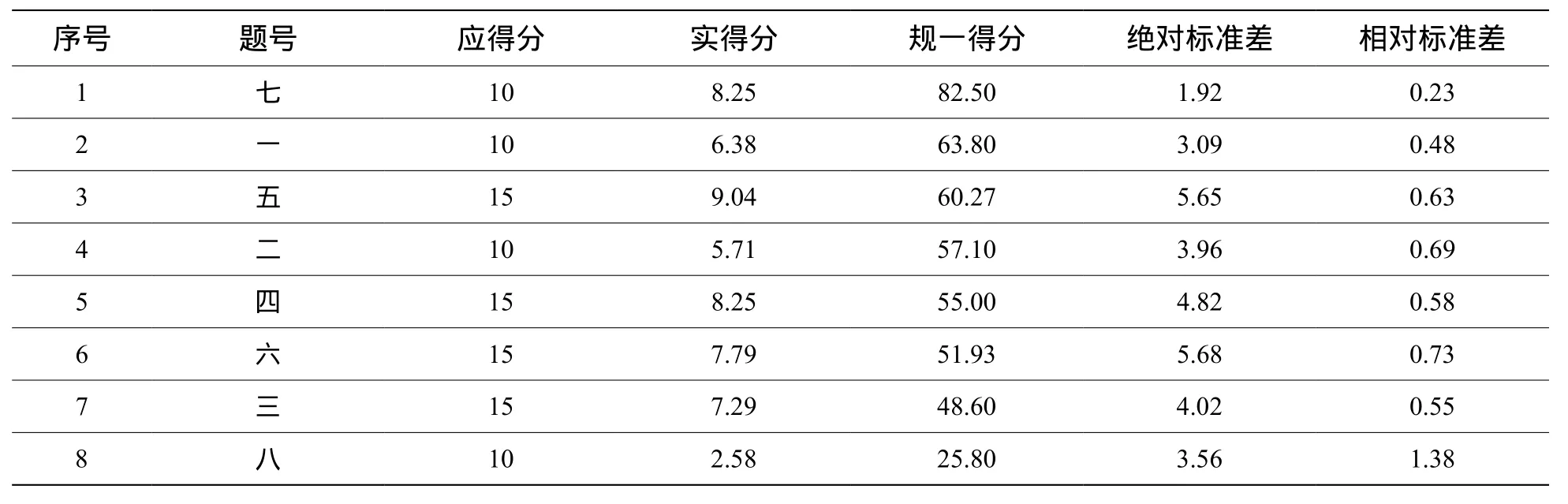
表6 3班各题得分
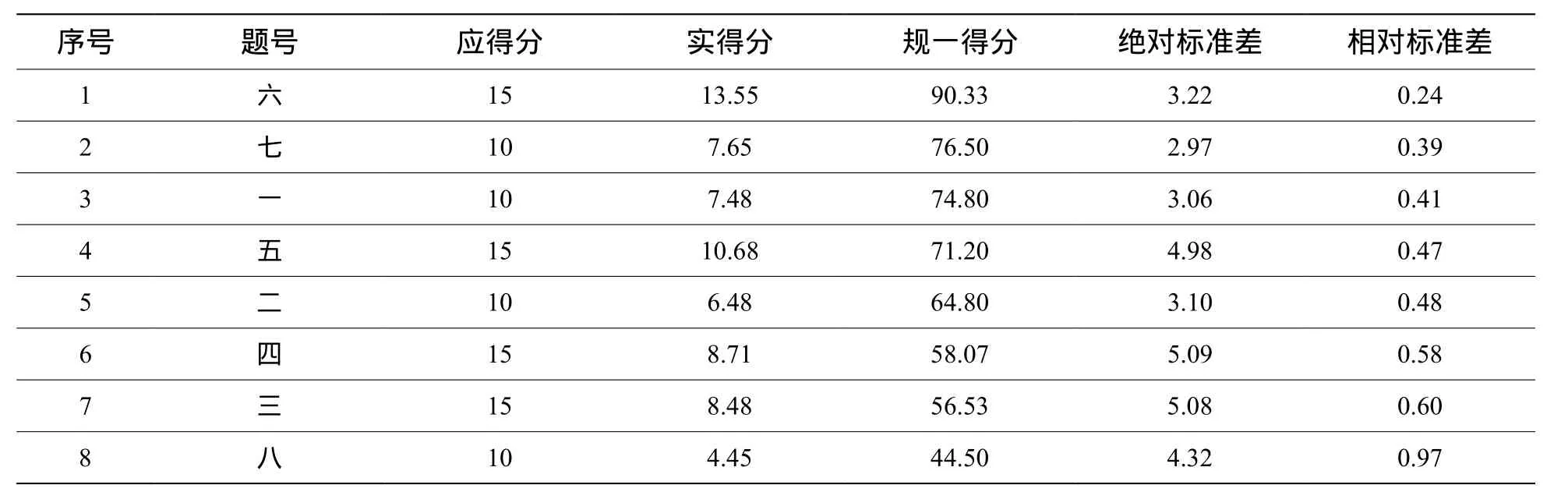
表7 4班各题得分
对比表7和表8发现,“好班”的成绩不仅较“差班”好,而且标准差也较小。对于“好班”,第一、五、七题的难易程度已经比较适中了,标准差也算合理。但对于“差班”,除第七题外,第一、五题仍然显得有点难,特别是第一题在教师看来是一个送分的简答题,得分居然刚过及格线!通过查看试卷后发现,学生的综合概括、文字表达能力较弱,这与中国学生习惯于别人为自己做总结不无关系。4班此题得分为74.8,符合预期,说明该班学风较好或者是考前复习到位。
根据以上分析,笔者得到的结论是:第一、五、七题的难易程度比较适中,班级差异比较明显。
3.6 难题分析
每次考试总会出现一些所谓的“难题”,但是难题未必就是真正的难题,很可能是某个教学环节出现了问题,比如说教师没有讲清楚、试题叙述不清、试题太偏、学生复习有问题等。因此,对难题进行分析十分必要。另外,对真正的难题进行有效的分析还是提高教学水准一条重要的途径。由于篇幅限制,笔者仅对第三题和第八题进行分析,不再区分“好班”与“差班”。
(1)第三题得分49.07,标准差0.61,得分低,标准差大。此题为分层设计题,要求学生用层次性方法设计一个组合逻辑电路,以便测试学生运用分层思想解决复杂问题的能力。从答题情况来看,得分低的主要原因是大部分学生不会用层次性方法对事物进行抽象,说明过去学科方法论教育非常欠缺,急需加强。
(2)第八题得分30.6,标准差1.26,得分很低,标准差很大,说明绝大多数学生没有掌握解题要领,只有少数学生过关,且得分很高。此题属于第七章,是该学期新增的教学内容。很多人得满分表明此题并不难,只要教学过程处理得当就会有好的结果。
分析难题得到的结论是:难题其实并不难,标准差过大也许与学生的个体差异或评分标准中得分点划分过粗有关。这些难题中有3个是考“能力”的题目,学生的能力确实有待师生双方共同努力而得以提升。
3.7 结论与改进措施
(1)考前教师没有上复习课,也没有给予任何暗示,试卷中没有可以“猜”的题目,因此考试成绩反映了教和学的实际情况,可以为持续改进提供真实的数据支持。
(2)第一、五、七题对“好班”来说已经达到理想的正态分布,其他班呈正偏态分布。第六和第八题因为一些特殊原因成绩不够理想。第二、三、四题所表现出的问题较多。
(3)所讲各个章节的教学过程必须保持完整,特别是最后一章的习题不能放弃不做。
(4)学生个体差异较大也许是一个不争的事实,提高学习积极性任重道远。
(5)标准差大可能与评分点划分不够详细有关,评分标准需要进一步细化。
(6)要加强学科方法论教育。
(7)要通过求简化真值表和做状态图,加强抽象思维能力训练。

表8 1、2、3班全体学生各题得分
4 结 语
考试是检查课堂教学质量的重要手段,应该得到足够的重视。学科方法论必须成为课程的重要内容,在考试中也必须作为重要考点。详尽的试卷成绩分析可以发现教学中存在的许多问题,为提高教学质量提供有效支持。

