小波阈值降噪在GPS伪距单点定位中的应用

王梦樱,冯茗杨,于杰

(山东科技大学 测绘科学与工程学院，山东 青岛 266590)

0 引 言

从信号频率的角度分析,全球定位系统(GPS)信号中的有用成分与噪声都是分布在一定的频率范围内的,呈现出低频特性,分布在低通滤波的结果中,而多路径效应与接收机噪声在整个时域/频域内则是全局分布,呈现出高频特性,分布于高通滤波的结果中．在GPS定位误差中,偶然误差很难选取固定的模型对偶然误差进行减弱,因而,采用相应的方法减弱其对定位精度的影响具有重要的意义．目前,对GPS数据降噪平滑的方法主要有小波分析与Kalman滤波等方法[1-2],由于小波分析具有良好的时频局部性,并且可以通过小波变换对信号进行分解,提取信号中的有用成分,分离噪声,被逐渐应用于GPS领域中,主要有相位观测值周跳的探测与修复[3-4]、GPS观测值的小波阈值降噪策略对比研究[5-7]、GPS精密单点定位与基线解算中多路径效应与接收机噪声等偶然误差的预处理与GPS数据预处理软件的开发等[8-10]．基于此,本文使用MATLAB语言设计了降噪策略,采用离散正交小波db3,Huristic SURE阈值选取规则,分解层数为2,对两个时段的静态GPS伪距观测值C1进行了降噪处理,分析了两个时段降噪前后GPS伪距单点定位的精度的变化情况．

1 小波分析的基本原理

小波分析是一种时间-尺度(时间-频率)的分析方法,该方法在时间-频率上都具有表征信号局部特征的能力,具有多分辨率的特点．设函数

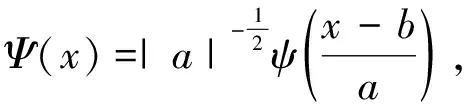
(1)

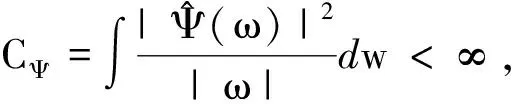
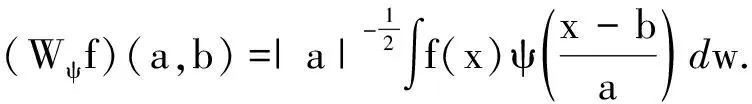
(2)

上述积分变换为f(x)以Ψ(x)为基的积分连续小波变换,a为尺度因子,b为平移因子．

小波变换的基本思想是用一组函数去表示或逼近某一信号或函数．为了计算方便,在实际应用中,需将连续小波及其变换离散化,取

代入式(1)可得:

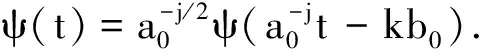
(3)

实值函数f(t)的小波变换为

Df(j,k)=〈f(t),ψj,k(t)〉

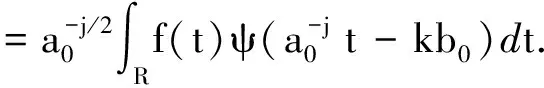
(4)

当a0=2,b0=1,时,式(3)就变成了二进小波[13]:

ψ(t)=2-j/2ψ(2-jt-k);j∈Z,k∈Z.

察两组护理满意度情况，将调查问卷发放给50例患儿家属代替填写，总分数为100分，90分以上即为满意，60～90分即为一般满意，60分以下即为不满意。总满意度=满意度+一般满意度。

(5)

及其变换:

Df(j,k) =〈f(t),ψj,k(t)〉

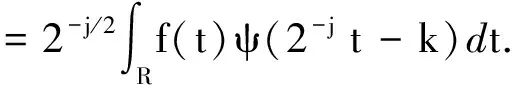
(6)

2 小波阈值降噪算法的程序设计与

降噪流程

2.1 程序模块

1)RINEX文件的读取与分解模块:用于生成各卫星的一维观测值时间序列,作为小波分解的原始信号;

2)小波降噪模块:设置降噪小波函数、阈值选取规则与分解层数,对原始信号进行降噪处理,生成降噪后的观测值时间序列;

3)信号组合模块:对降噪后同一历元下的一维信号进行组合,形成新的观测值文件;

4)伪距单点定位模块:分析观测值信号降噪前后定位精度的变化．

2.2 小波阈值降噪流程

GPS观测值可以简单地表达成:

ρ(t)=P(t)+B(t)+e(t),

(7)

式中:P(t)为卫星信号传播的几何距离;B(t)为测量值的偏差;e(t)为观测噪声．通常将GPS的观测噪声视为白噪声[6,9],这一类误差在时域上建模比较困难,因而我们可以使用小波变换在频域上对其进行分析．具体的降噪流程为:

1)分解观测值时间序列,选择合适的小波(dbN),并确定小波的分解层数n,对信号进行n层小波分解;

2)高频系数的阈值量化,对各层的高频系数选择一个软阈值进行阈值量化处理;

3)小波的重构,根据各层分解的低频系数和阈值量化处理后的高频系数,进行一维信号的小波重构得到消除噪声的观测值．

将上述程序模块与小波阈值降噪流程相结合,设计流程图如图1所示.

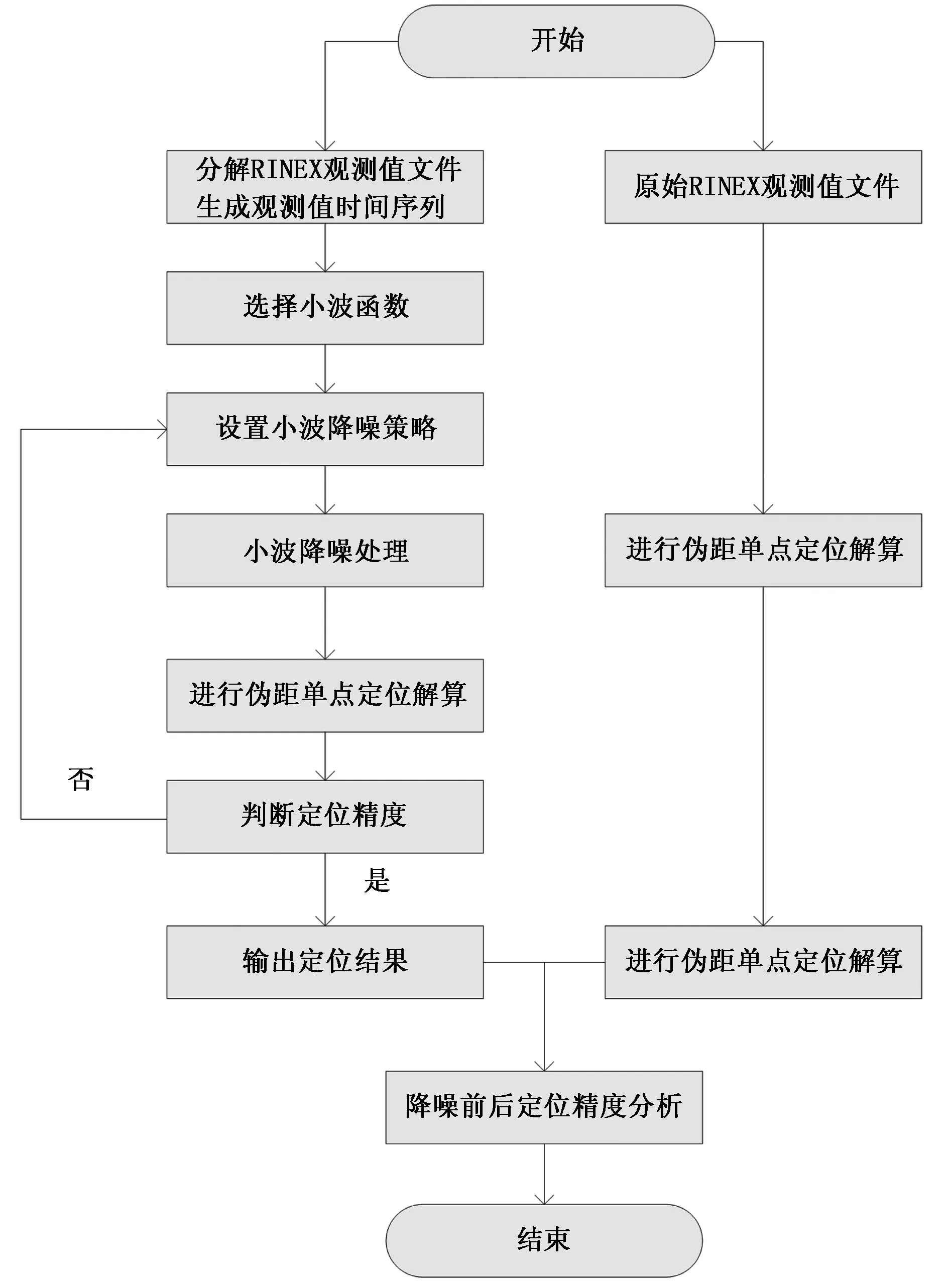
图1 小波阈值降噪流程图

3 实验分析

3.1 原始数据的采集与分析

实验中使用海星达H32型接收机，架设在校园已知控制点静态模式下观测,选取其中两个时段的数据作为降噪分析的原始数据,并对两个时段GPS卫星的高度角变化情况统计如表1所示.

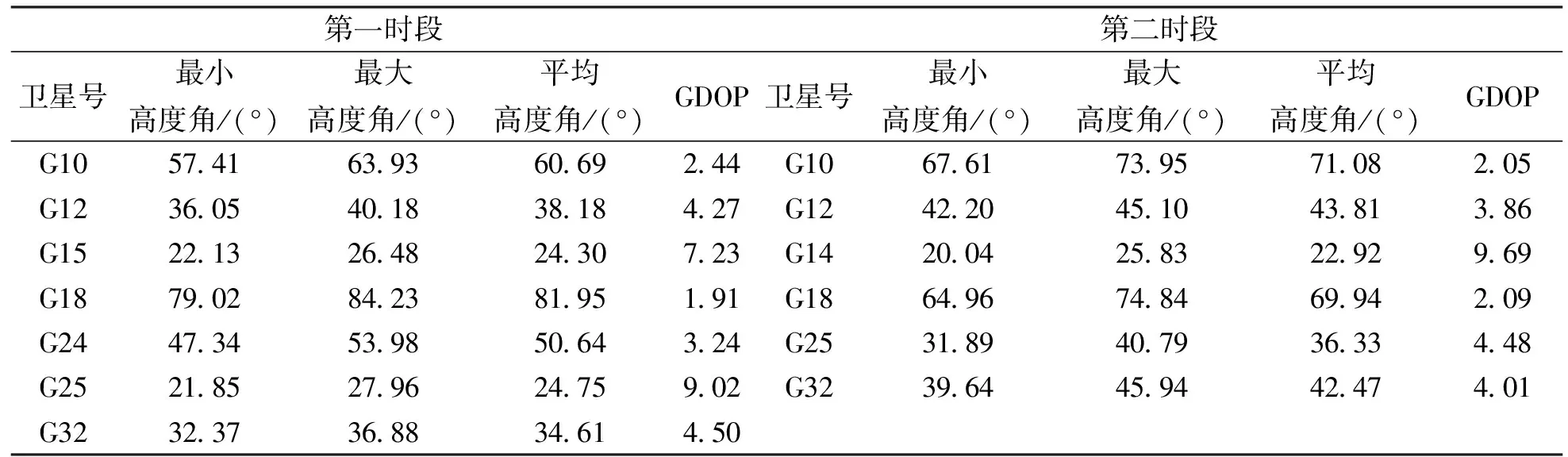
表1 两个时段GPS卫星高度角变化情况表

由表1可以看出,上述两个时段的GPS卫星的高度角变化情况比较常见,在第一时段G15、G25两颗卫星高度角较低,从而会影响了第一时段的数据质量,在第二时段,卫星高度角仅有G14一颗卫星高度角较低,并且两个时段共有的卫星中(如:G10、G12、G32、G25)在第二时段的卫星平均高度角和GDOP也都优于第一时间段．从而,可以初步分析得知,第二时段的数据质量与定位精度要高于第一时段．

3.2 数据降噪分析

对GPS伪距观测值C1的小波阈值降噪策略选在MATLAB环境下,采用db3小波,Huristic SURE阈值选取规则,分解层数n=2,对GPS伪距观测值C1进行了降噪处理,对降噪前后GPS伪距单点定位精度的变化分析如下:

1)观测值降噪前后,定位结果中X/Y/Z方向各历元的解与各方向平均值的偏差(如图2、图3所示);

2)观测值降噪前后,定位结果中X/Y/Z方向各历元的解与真值的偏差(如图4、图5所示)．

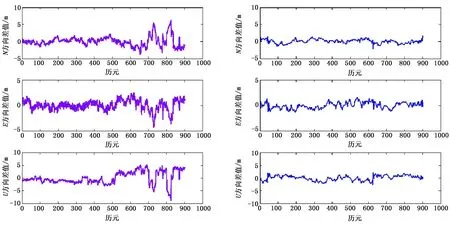
图2 第一时段降噪前后N/E/U方向各历元的解与各方向平均值的偏差

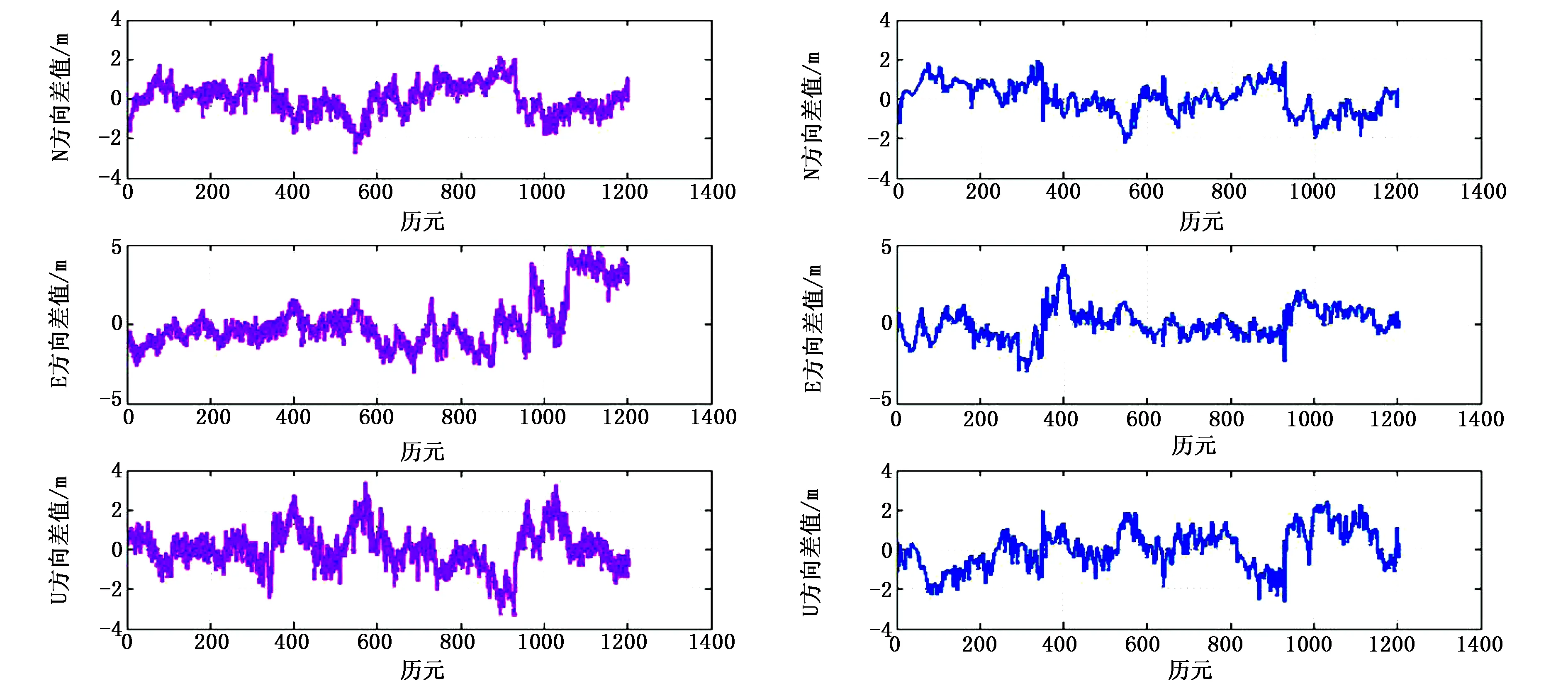
图3 第二时段降噪前后N/E/U方向各历元的解与各方向平均值的偏差

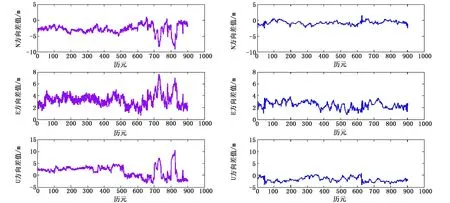
图4 第一时段降噪前后N/E/U方向各历元的解与各方向真值的偏差

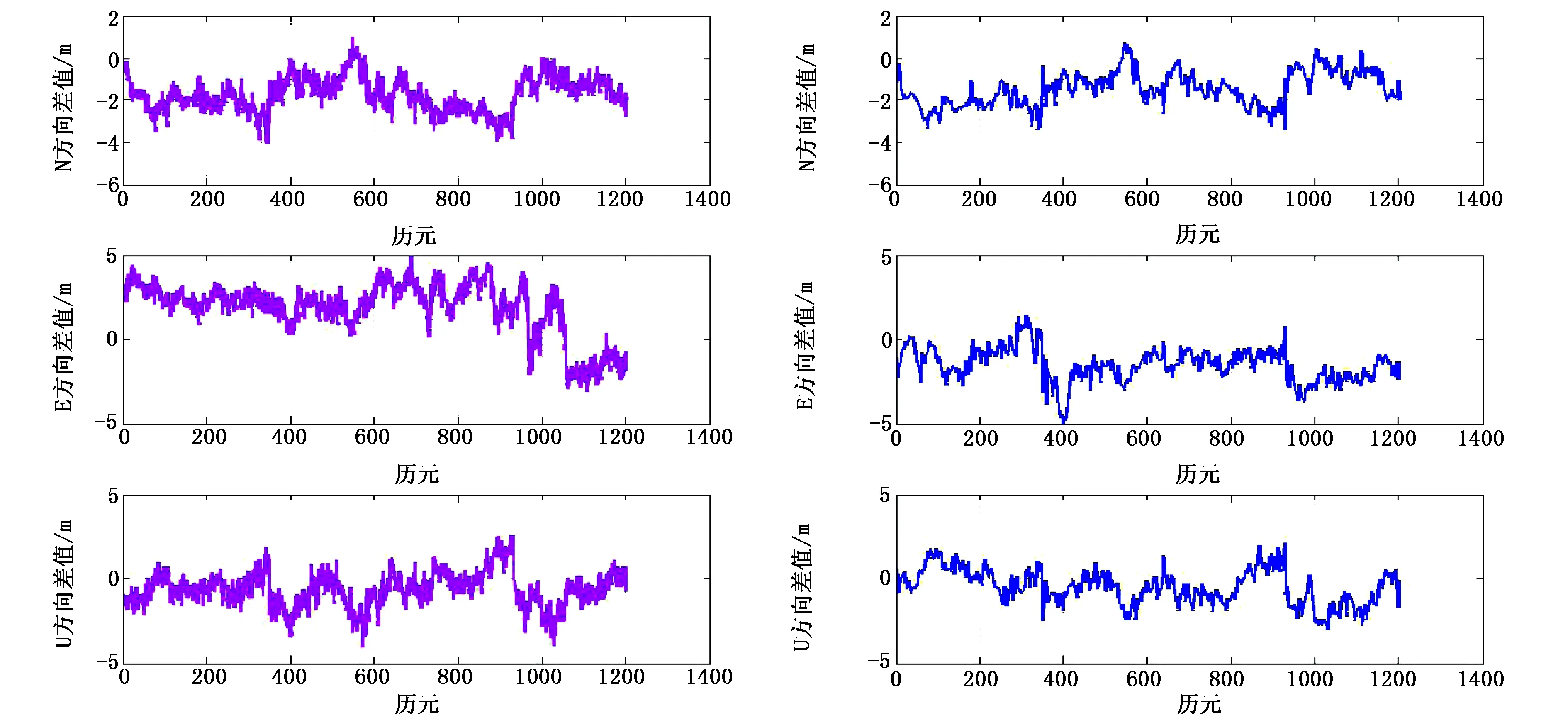
图5 第二时段降噪前后N/E/U方向各历元的解与各方向真值的偏差

进一步对比分析了观测值降噪前后的内符合精度、外符合精度与偏差三项指标的变化情况,将以上参数统计成表格形式,具体统计如表2所示.

表2 观测值降噪前后定位精度情况统计

根据图2至图5、表2对降噪前后定位精度的统计情况,总结如下:

1) 由图2、图4分析可知,第一时段中第600至900个历元时X/Y/Z方向各历元的解与各方向平均值、已知控制点坐标真值相比,变化幅度较大．根据对各卫星的高度角统计可知,在此时段G12、G15、G25、G32四颗卫星的高度角较低,从而使得原始数据中含有较多的噪声,导致了上述现象．

2) 根据表2统计可知,第一时段与第二时段相比,定位精度低,数据质量较差,与表1中的结论一致．由表2可知,该时段原始数据经降噪处理后定位精度提高了31.93%．

3) 由图3、图5分析可知,第二时段X/Y/Z方向解算结果与各方向平均值、已知控制点坐标真值相比,变化趋势比较稳定,定位精度较好,因为在与第一时段观测条件下相同的情况下,该时段卫星的平均高度角较高,受到的多路径效应等噪声的影响较小．由表2可知,经降噪处理后,定位精度提高了16.02%．

4 结束语

小波阈值降噪法可以有效地从GPS信号中分离噪声和有用信号,对进一步提高GPS定位精度、减弱GPS观测中多路径效应与接收机噪声等偶然误差的影响有显著作用．同时,在受噪声影响较大的时间段的对观测值的降噪处理效果比较明显．