利用多面函数拟合和欧拉矢量法建立福建省GPS速度场模型

杜仲进

(福建省测绘院,福建 福州 350003)

0 引 言

GPS速度场表征布满整个地面空间的GPS站运动速度构成的物理场,在地球科学领域具有极其重要的作用．例如,坐标转换时常常需要进行历元和框架的转换,而历元转换则需要速度场;大地测量参考框架的动态维持也需要速度场[1-2];大陆地壳形变分析及其动力学机制解释更需要速度场[3-9],等等．随着GPS技术的推广普及,目前全国各区域均已建成高度密集的GPS观测网,通过多年观测资料的积累,现足以构建起大密度的各区域GPS速度场,对今后维持高精度动态区域坐标参考框架和构建精细的区域地壳形变场具有深远的意义．

尽管目前区域GPS观测站已经足够密集,但是由于各种条件的限制,GPS观测站通常呈非均匀分布,基于这些站的观测资料构建的速度场也是离散分布的,然而,均匀连续分布的速度场才更有实用价值,因此,构建速度场模型成为必需．速度场模型构建方法有很多,概括来讲,主要包括常规数学方法和地球物理方法两大类．其中,数学方法主要是通过拟合建立速度场,不需要考虑其地学意义,如多面函数拟合法[10]、双三次样条函数拟合法[11]、有限元插值法[12]、最小二乘配置法[13-14]、Kriging插值法[15],等等;而地球物理方法主要是依据刚体运动学原理来计算欧拉旋转矢量建立速度场,具有明确的地学意义,如全域欧拉矢量法和局域欧拉矢量法[1,16]．基于上述两大类方法,众多研究人员开展了速度场建模研究．刘经南等[10]利用多面函数拟合得到均匀分布的中国地壳平面运动整体速度场,该方法不需要细分块体,能有效逼近地壳运动细微特征,比计算欧拉矢量法更适合于中国平面地壳运动速度场模型的建立[17]．江在森等[14]应用最小二乘配置原理建立水平运动速度场统一模型,获得包含误差噪声的GPS实测速度场和相对于不同参考基准的经误差噪声滤波后的连续分布速度场．刘晓霞等[15]采用Kriging插值法构建了网格化的GPS速度场,与最小二乘配置结果具有高度的一致性．谢方等[18]分别利用Kriging插值法和最小二乘配置法建立中国大陆5个块体速度场模型,通过外部检核发现,最小二乘配置拟合精度较高,稳定性较好．吴富梅等[16]采用移动窗口法筛选局部区域点,从而利用局域欧拉矢量法建立了CGCS2000速度场模型,其精度相比中国全域欧拉矢量及块体欧拉矢量速度场模型有明显的提高．

1 速度场模型介绍

1.1 多面函数拟合法

多面函数拟合法是速度场建模常采用的方法之一,其基本原理为[10]:任何一个圆滑的数学表面总可用一系列的有规则的数学表面的总和以任意精度逼近．假定数学表面上一个点的大地经纬度坐标为(b,l),该点的速度值为v(b,l),则多面函数拟合模型可表示为

(1)

式中:v(b,l)表示坐标水平方向南北分量或东西分量的速度值;n为结点的个数;αi(i=1,2,…,n)为待估参数;Q(b,l;bi,li)为核函数,在地学中一般采用正双曲面核函数:

Q(b,l;bi,li)=[(b-bi)2+(l-li)2+δ2]β,

(2)

式中:δ2为光滑因子,可取0或某一较小数值,需要根据实际数据研究确定;β通常可取-0.5、0.5、1等．

本文采用的有实测速度值的基准站共计74个,其中,64个为建模点,10个为检核点．从建模点中选取了12个在福建省内均匀分布且稳定性良好的基准站作为多面函数的结点,因此,多面函数拟合的观测方程表示为

(3)

即:

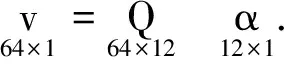
(4)

误差方差为:

四是注重心理素质健康教育培训。针对监狱戒毒警察工作生活中面临的监管安全压力、执法安全压力等导致的心理问题，河南省司法厅联合高校举办由政工干部和基层业务骨干参加的心理健康教育能力素质提升培训班，引导政工干部把心理矫治的手段运用到干部思想政治工作中，引导基层一线警察掌握释放自我、缓解压力的手段和方法。各直属单位也把队伍心理健康教育作为教育培训的重要内容，定期邀请社会心理咨询专家或利用单位内部心理咨询师对警察开展心理辅导、心理知识讲座、心理咨询、心理拓展、心理矫治等心理素质培训，使队伍掌握应对压力和解决心理问题的方法技巧，有效缓解工作生活压力，提升心理健康水平。

Vv=Qα-v.

(5)

顾及速度值的权,则待估参数的最小二乘解为

α=(QTPvQ)-1QTPvv.

(6)

速度拟合值的均方根误差为:

(7)

1.2 欧拉矢量法

欧拉矢量法也是速度场建模经常采用的一种方法,这种方法在刚性块体上最为适用．研究表明,福建省位于华夏陆块[19-20],而华夏陆块是经历了与周边板块碰撞、裂解、再拼合等复杂的地质构造活动而形成的刚性块体,因此在该陆块上采用欧拉矢量法进行速度场建模具有科学依据和地学意义．

采用64个建模点构造欧拉矢量法观测方程为:

(8)

考虑到在地学中NEU坐标系使用的普遍性,采用正交变换矩阵将地心直角坐标速度变换为NEU坐标速度,其中,变换矩阵表示式为

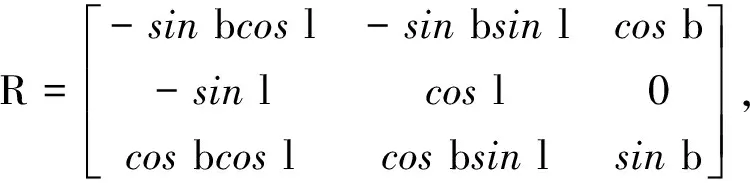
(9)

式中,b、l为大地纬度、经度．

2 数据处理方法

数据处理和速度场建模流程详见图1．首先，采用高精度数据处理软件GAMIT[21]计算2013-2015年84个FJCORS基准站坐标和卫星轨道的单日松弛解．由于基准站数量较多,将其分成3个子网解算,同时,引入国内及周边15个IGS跟踪站进行同步处理,以便后续实现ITRF2008参考框架．其次，将3个子网的单日松弛解文件与IGS提供的全球8个子网的单日松弛解文件进行合并,得到包含FJCORS基准站(以下简称基准站)和全球IGS站的坐标、卫星轨道和极移等参数的单日松弛解及其方差-协方差矩阵．利用GLOBK[22]软件进行Kalman滤波,并通过7参数相似变换,将基准站坐标变换到由全球均匀分布的若干IGS稳定站所维持的ITRF2008框架坐标, 从而获得基准站ITRF2008参考框架下的单日解坐标时间序列．进而对各基准站坐标时间序列进行分析和编辑处理,由于有10个基准站的观测数据不足1年或因基准站不稳定而导致速度值明显离群,因此对这10个站进行剔除,实际采用74个基准站,修复因基准站迁站及其设备、天线更换等导致的阶跃,剔除因观测环境不佳、接收机内部噪声增加、数据传输的误码率等导致的少数离群值．最后,得到74个基准站较为平滑的时序结果,并通过线性拟合得到各基准站的实测速度值．在基准站实测速度值的基础上,随机选取了64个站用于建立速度场模型,剩余10个作为检核点用于检验模型的精度．

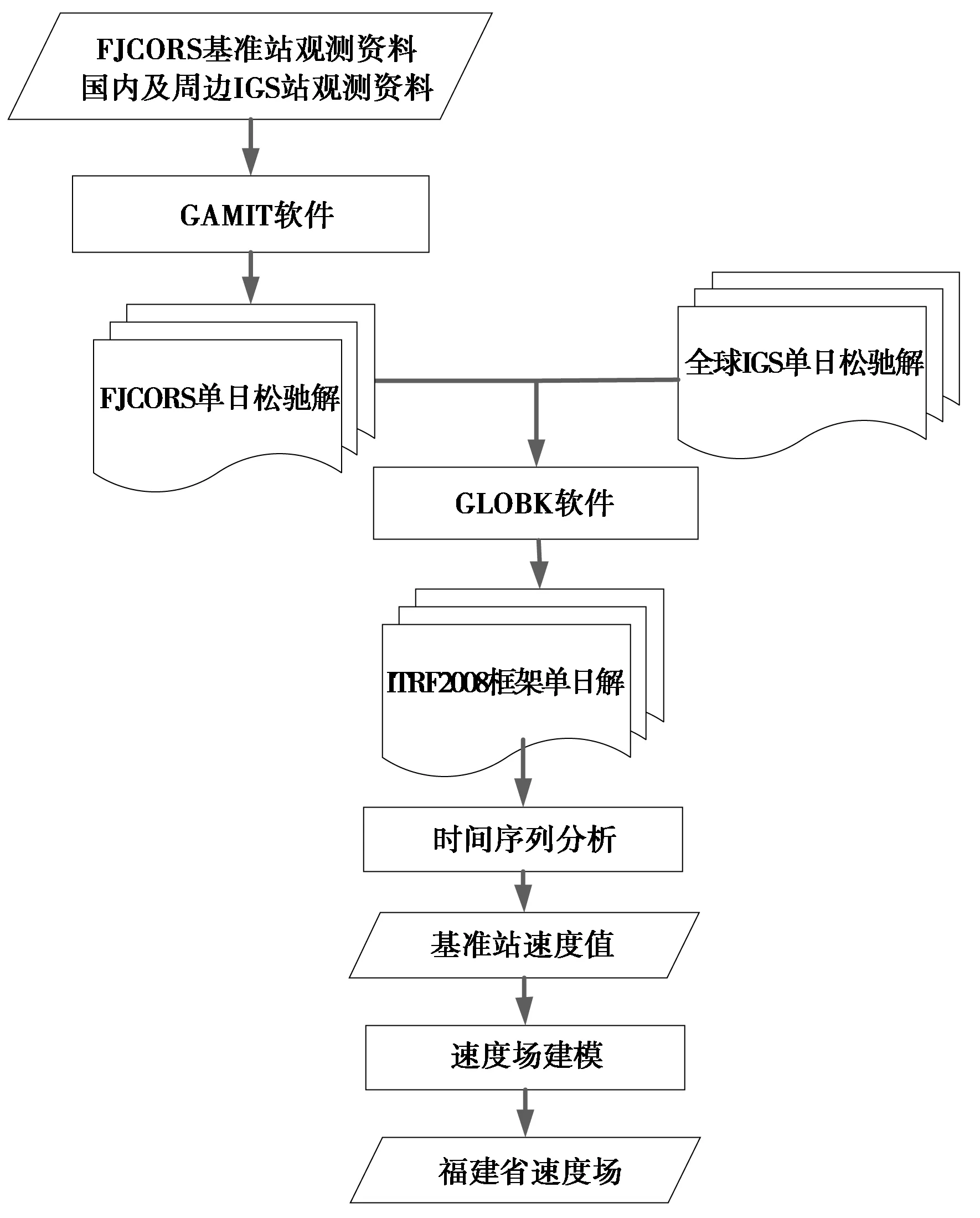
图1 数据处理流程图

3 速度场建模算例分析

根据节1介绍的两种速度场建模方法原理,本文通过MatLab程序设计构建了福建省及周边区域水平方向速度场模型．其中,模型的内符合精度以速度模型残差的均方根误差表示,将其统计在表1中,结果表明,采用两种方法建立的速度场模型均具有较高的精度,且精度相当．

表1 速度场模型的内符合精度mm/a

方法南北分量精度东西分量精度 多面函数拟合法1.062.00 计算欧拉矢量法1.361.22

为了进一步检验速度场模型的精度,本文统计了检核点的模型值与实测值的较差,详见表2,两种方法得到的检核点速度较差在±2.28 mm/a以内,表明两种速度场模型均具有较高的准确度．

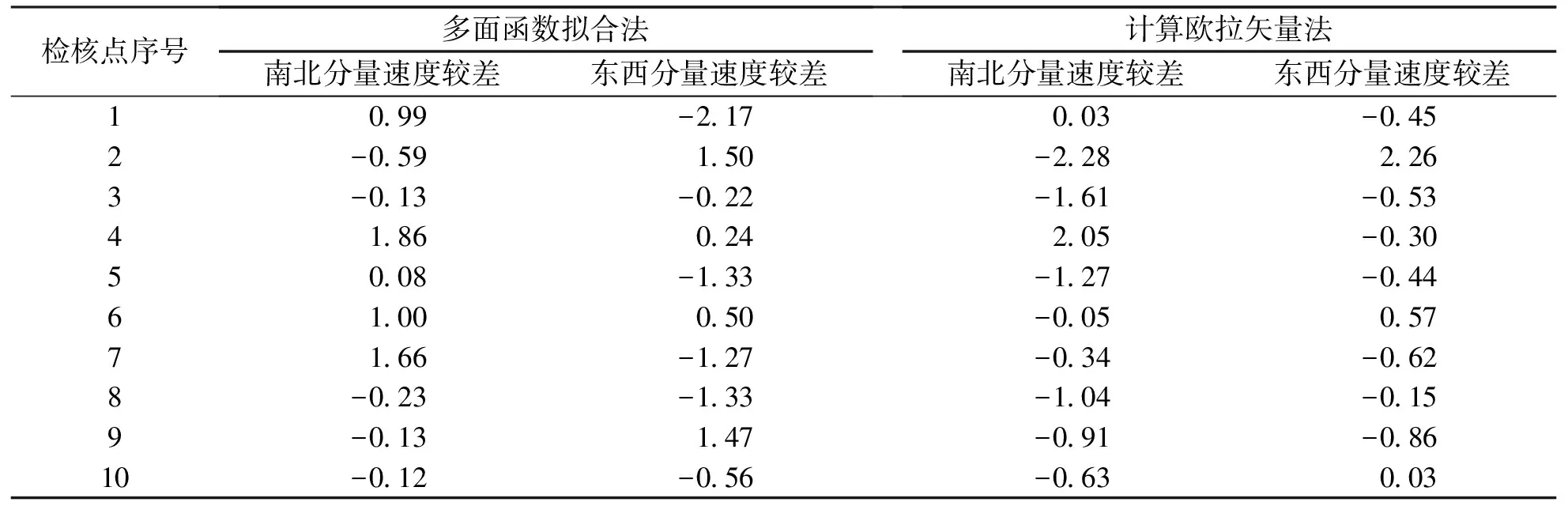
表2 速度场模型的外符合精度mm/a

本文在构建速度场模型的基础上,将福建省及周边区域划分成0.5°×0.5°网格,共计100个网格点,将速度场模型值绘制在网格点上,详见图2,图中灰色实线表示断层．速度场网格化结果显示,在福建省陆域内,多面函数拟合法与欧拉矢量法得到的结果具有高度的一致性．两种结果均显示,福建省陆域内的运动速度为35 mm/a左右,运动方向为SE-E向．

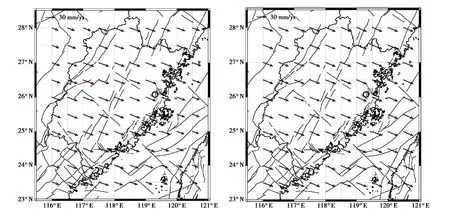
(a)多面函数拟合法 (b)欧拉矢重法图2 多面函数拟合法和欧拉矢量法获得的速度场

4 结束语

本文在获取福建省GPS站实测运动速度值的基础上,分别采用多面函数拟合法和欧拉矢量法构建福建省及周边区域GPS速度场模型,主要获得以下结论:

1)两种方法模拟的速度水平各分量精度均优于2.00 mm/a;同时,检核点的速度模型值与实测速度值的较差均在±28 mm/a以内,表明所建立的速度场模型具有较高的精度和可靠性．

2)在福建省陆域内,两种方法得到的速度场具有高度的一致性,结果均显示,福建省陆域内的运动速度为35 mm/a左右,运动方向为SE-E向．

除了上述两种方法,速度场建模方法还有很多,今后可以采用多种方法进行尝试,更深入地研究各种建模方法的效果,为坐标转换、大地测量参考框架动态维持和区域地壳形变分析提供有效保障．