对流层映射函数对GNSS反演可降水量的影响分析

黄逸宇,魏冠军,任瑞

(1. 兰州交通大学 测绘与地理信息学院,甘肃 兰州 730070;2. 地理国情监测技术应用国家地方联合工程研究中心，甘肃 兰州 730070；3. 甘肃省地理国情监测工程实验室,甘肃 兰州 730070)

0 引 言

自Bevis[1]提出地基全球卫星导航系统(GNSS)反演大气可降水量后,其高时空分辨率、全天候、高精度等优点使GNSS水汽探测技术在气象学领域得到广泛应用[2-6]．大气可降水量(PWV)在大气能量传输和天气系统演变中起到了十分重要的作用,尤其是对中小尺度灾害性天气的实时监测具有指示意义[7]．天顶对流层延迟(ZTD)可分为静力学延迟分量(ZHD)和湿延迟分量(ZWD)两部分[8-11]．PWV是由ZWD与区域转换因子的乘积求得,而映射函数是将ZTD转化为信号传播路径延迟的关键模型．因此,映射函数模型的选择对于提高PWV反演精度和GNSS定位精度有十分重要的意义．近年来,国内外学者开展了关于映射函数对GNSS数据处理方面影响的研究．Boehm等[12]利用22年的全球VLBI数据对NMF(Niell Mapping Function)模型、VMF1(Vienna Mapping Function 1)模型和GMF(Global Mapping Function)映射函数模型进行了分析,结果表明,使用VMF1模型可以得到更高的基线解算精度;李斐等[13]通过NMF、VMF1、GMF 映射函数模型分析南极地区国际GNSS服务机构(IGS)站的基线解算数据,结果表明在南极地区,VMF1的精度结果略好于GMF和NMF;刘宗强等[14]利用陆态网数据对NMF、VMF1、GMF模型在不同截止高度角下的基线解算精度进行了分析,结果表明在各个截止高度角下3种映射函数对陆态网基线解算精度影响差别不大;汪进新等[15]利用NMF、VMF1、GMF映射函数模型对武汉站(WUHN)和拉萨站(LHAZ)反演PWV的精度进行了初步探讨,结果表明当有实测气象数据时,VMF1的反演精度要优于GMF．针对目前关于映射函数对反演PWV精度的研究较少,且没有考虑多种变量对映射函数反演可降水量精度的影响．本文选取香港卫星定位参考站网(SatRef)中7个测站的数据,分别对NMF、GMF、VMF1 3种映射函数模型在不同季节、不同高度角的解算结果进行比较,分析3种映射函数在不同约束条件下对反演PWV的影响,比较不同解算策略下反演可降水量精度,为反演PWV的准确性以及在气象学研究和预报等方面提供一定的参考．

1 映射函数模型

映射函数模型大体可分为两大类:一类是基于多年观测资料建立的经验模型,如NMF模型和GMF模型;另一类是基于实测气象资料建立的模型,如VMF1模型[16]．NMF、VMF1、GMF映射模型都采用三项连分展开式,包括ZHD映射项和ZWD映射项两部分,这3种映射函数的主要差别在于系数a、b、c的计算方法不同．

1.1 NMF映射函数

Niell考虑到地表气象参数随纬度及时间的周期性变化,应用分布在全球的26个探空气球观测资料,顾及了南北半球和季节的非对称性建立了全球性,建立了NMF映射函数模型[17]．该模型忽略了气象元素对模型的影响．其中,ZHD映射项函数Mh(e)的具体形式为

(1)

式中：第一项为平均项,第二项为波动项;aht=2.53×10-5;bht=5.49×10-3;cht=1.14×10-3;e为高度角;H为正高;ah,bh,ch静力学映射系数,3个系数计算公式相同,当测站纬度在15°～75°之间时,ah可由式(2)内插求得:

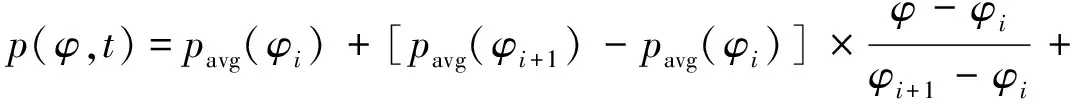
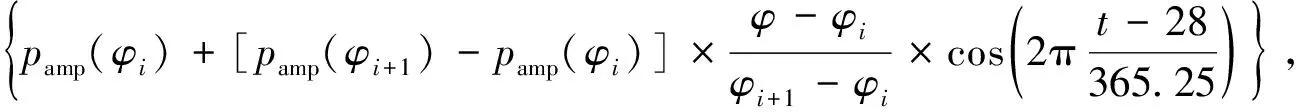
(2)

式中:φ为测站纬度;p为需要内插的系数ah,bh,ch;t为年积日;φi和φi+1时的系数平均值pavg和波动的幅度pamp值可以从文献[16]中查表获得．

湿延迟映射项函数Mw(e)为

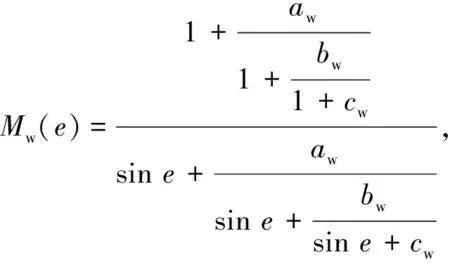
(3)

式中:e为卫星高度角;aw、bw、cw为湿延迟映射项系数;其计算方法与干延迟映射项相似,系数可通过文献[16]查表获得．

1.2 VMF1映射函数

VMF1模型是由维也纳理工大学利用欧洲中尺度天气预报中心(ECMWF)的数据建立[18],模型表达式与NMF类似,但模型中系数的求解方式与NMF不同．VMF1的系数ah、aw是该大学的大地测量研究所根据实测气象资料而生成的经差为2.5°、纬差2°、时间间隔为6 h的格网图提供的,用户可以在维也纳理工大学的网站上查询得到．而系数bh、ch则是根据ECMWF 40年的观测资料求得．其中bh=0.002 9;ch由式(4)计算:

(4)

式中:t为年积日;φ为测站纬度;c11、c10、ω均为常数,但其取法在南北半球有所差别:北半球时,c10=0.001,c11=0.005,ω=0;南半球时,c10=0.002,c11=0.007,ω=π．湿分量系数bw、cw一般分别取0.001 46和0.043 91．采用VMF1模型进行精密单点定位(PPP)精度较高,但该模型是基于实测气象数据得到,大约有34 h的延迟,实时性较差[19]．

1.3 GMF映射函数

为解决VMF1函数模型系数ah、aw的时延问题,Boehm等[12]通过将VMF1函数的参数在全球格网上进行球谐展开,提出了新的映射函数GMF,GMF函数将系数ah和aw表示为年积日t、测站的纬度、φ和高程H的函数;系数b、c的选取与VMF1相同,a则同样利用格网文件内插获得．GMF函数不仅消除了实测气象数据的延迟问题,且简化了计算过程．

2 算例分析

2.1 实验数据及解算方案

本文选取了香港地区卫星定位参考网中的7个站点在2017-3-20(北半球春分)、2017-6-21(夏至)、2017-9-23(秋分)、2017-12-22(冬至)共计4 d的数据作为模型解算数据,并引入BJFS、LHAZ、DARW三个IGS站点参与解算．如图1所示．采用京士柏气象探空站(HKKP)的无线电探空仪获取的可降水量数据作为GNSS水汽反演质量分析的真值．比较基线解算误差以及选用不同映射函数方案下的可降水量精度,分析不同解算方案对反演可降水量的影响．

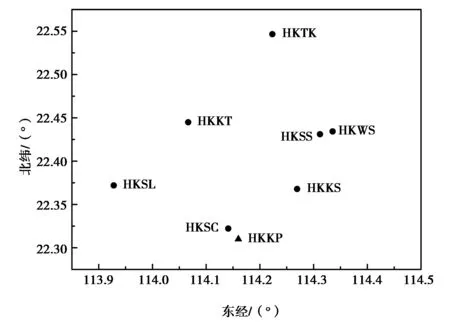
图1 SatRef站点分布图

为了对比不同解算方案对可降水量反演精度的影响,在GAMIT中将3个IGS站点设为固定站,站坐标约束为0.05 m、0.05 m、0.05 m,将香港地区SatRef中7个站点设为非固定站,站坐标约束为100 m、100 m、100 m．采用sp3精密星历,LCAUTCLN作为电离层模型,对流层折射模型采用Saastamoinen模型,参考框架使用ITRF2008,空间惯性参考系采用J2000．通过修改sestbl.文件参数,分别使用VMF1、GMF、NMF模型进行解算,并且分别设置截止高度角为10°、15°,利用GAMIT分别进行解算．

2.2 映射函数基线解算误差分析

GAMIT基线解算结果中的标准化均方根误差(NRMS)是用来表示单时段解算出的基线值偏离其加权平均值的程度．一般NRMS值越小说明其基线解算精度越高,其值一般在0.2左右摆动,小于0.3,则可以认为解算成功;若大于0.3,则表明解算结果有问题．需要检查解算数据的起算点坐标等,其计算公式为

(5)

从图2和表1可以看出,式(3)中映射函数在不同高度角下的解算的NRMS值均小于0.2,解算结果较好,三种映射函数在相同截止高度角的情况下NRMS值相差很小,总体来说GMF和VMF1的NRMS值要略小于NMF,说明VMF1和GMF处理测站数据的精度要比NMF高;且随着高度角的升高,3种映射函数的NRMS值都随之降低,说明SatRef站点的数据质量较好．

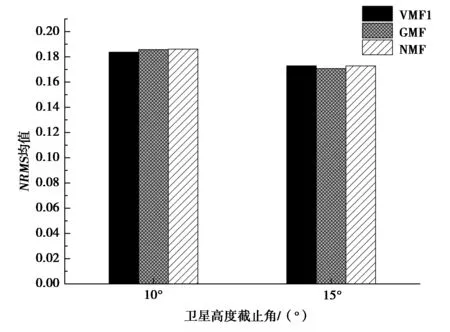
图2 不同卫星高度角NRMS均值

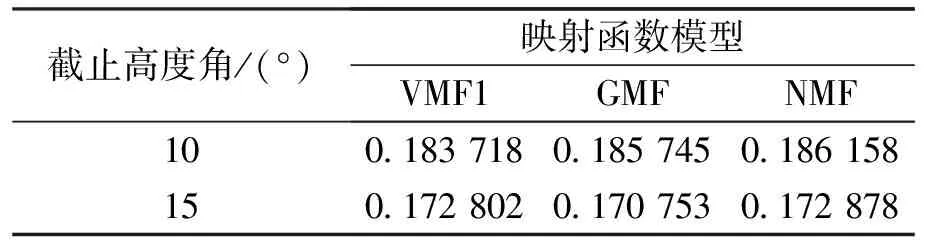
截止高度角/(°)映射函数模型VMF1GMFNMF100.183 7180.185 7450.186 158 150.172 8020.170 7530.172 878

从表2可以看出,不同高度角时,3种映射函数在N方向的误差均优于5 mm,E方向的误差优于9 mm,U方向的误差优于15 mm,说明三种函数在水平方向上的误差较小,垂直方向上的误差较大．随着高度角的增大,3种映射函数的误差在N、E、U方向上均增大,说明随着高度角的增大,所受对流层影响也相应增大,解算数据的精度随之降低,所以在解算测站数据时推荐使用10°高度角作为解算截止高度角．同一高度角时,三种映射函数的精度在N、E、U方向上差别不大,但VMF1和GMF的精度高于NMF．由于GMF是由VMF1的参数进行球谐展开而得到,具有很好的连续性．且VMF1需要实测气象参数以及时延问题,所以在进行网基线解算时推荐使用GMF映射函数．

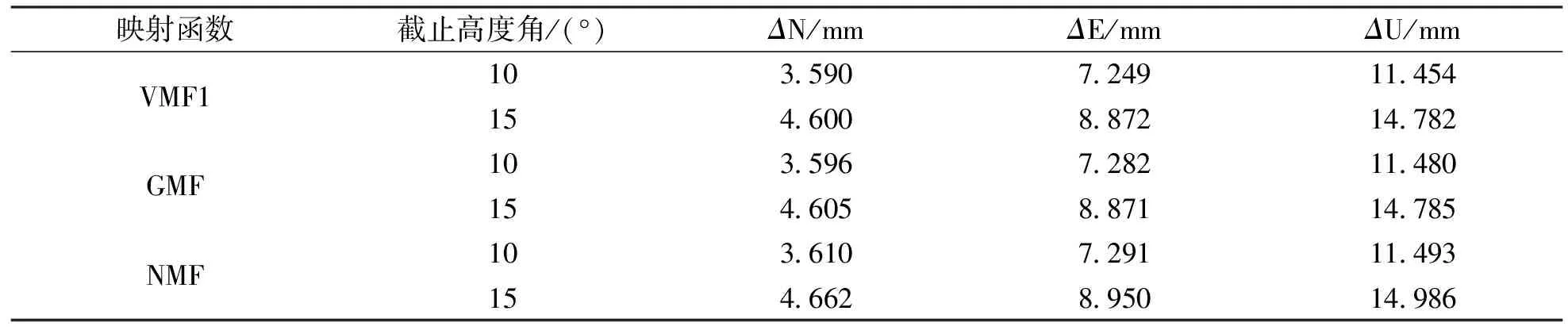
表2 基线平均误差

2.3 映射函数反演GNSS可降水量精度分析

对流层延迟(ZTD)是由静力学延迟(ZHD)和湿延迟(ZWD)组成,ZHD占整个对流层延迟的90%左右,在大气中比较稳定,一般采用Saastamoinen模型求解．ZWD虽然只占3%～10%,但在大气中的变化却相当剧烈．由于ZWD难以精确求得,一般利用ZTD与ZHD的差值来求得ZWD,如式(6)所示．ZWD是计算PWV的基础,其计算公式如式(7)所示．

ZWD=ZTD-ZHD,

(6)

PWV=∏×ZWD.

(7)

式中,Π为转化因子,是关于加权平均温度的函数．在香港地区,若没有实测地面温度资料时可以取Π=0.162[20]．

香港探空站HKKP每日探空数据的采样间隔12 h,而GAMIT解算ZTD的采样间隔为2 h,所以在利用ZTD解算可降水量时,将反演可降水量的采样间隔同化为12 h．利用GAMIT求出不同映射函数方案的ZTD值,并用Saastamoinen模型求得ZHD,然后根据式(7)求得可降水量．比较各个解算方案反演可降水量的精度．由于篇幅有限,本文仅给出HKSC站的ZTD分布曲线图和不同方案解算PWV值分布曲线，如图3所示．

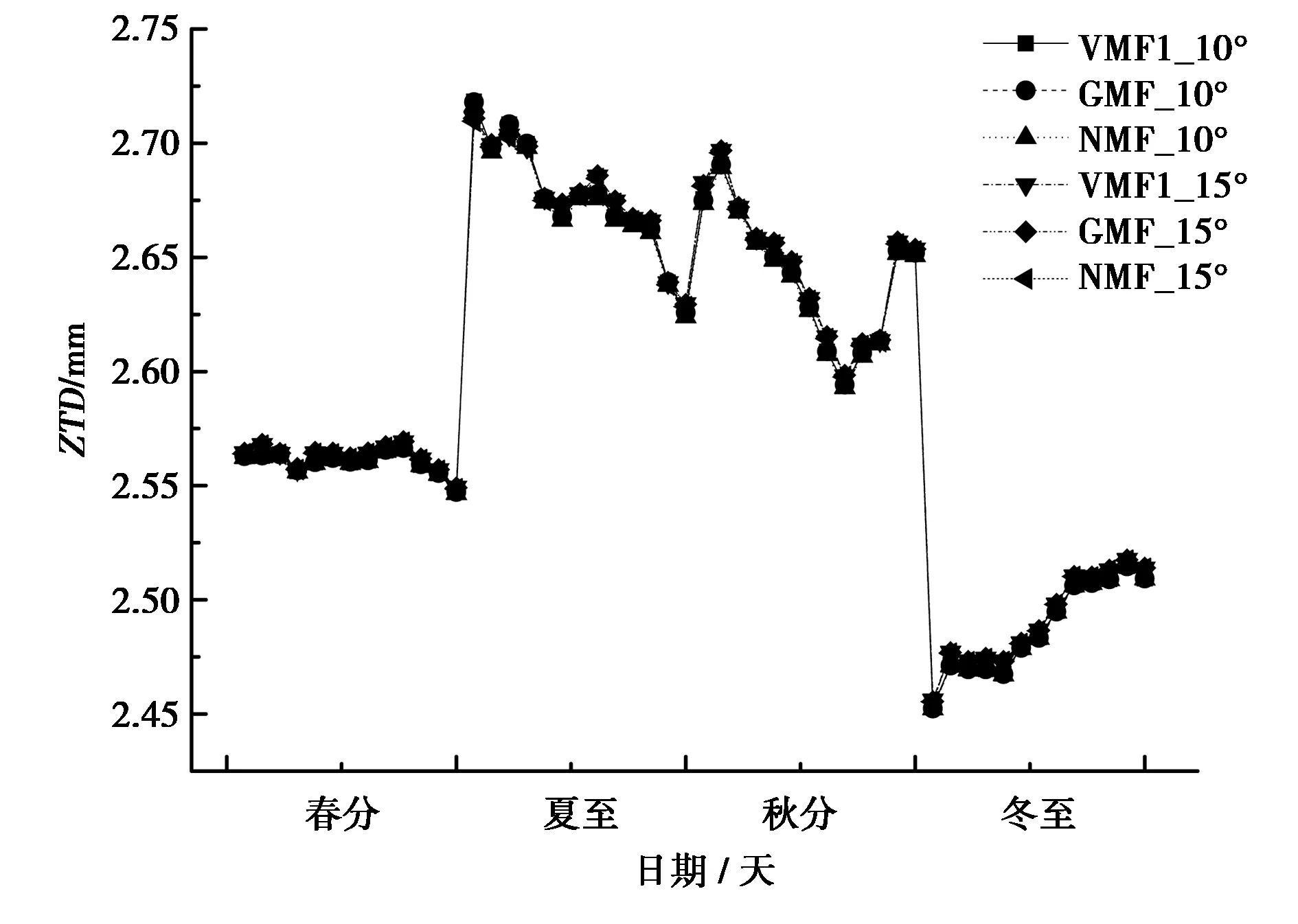
(注:VMF1-10°表示在截止高度角为10°时VMF1函数的解算结果,下同)图3 HKSC站不同季节解算ZTD分布图

表3 HKSC站4d解算ZTD均值

由图3和表3可以得出:不同方案解算出的ZTD基本趋于一致,夏至和秋分时ZTD明显高于春分和冬至,基本符合香港地区夏秋多雨的季节变化特点．在相同高度角时,三种解算方案差别较小,在0.5 mm左右;而不同高度角时,同一映射函数模型解算的15°高度角ZTD值均比10°高度角解算的ZTD值高2～5 mm．

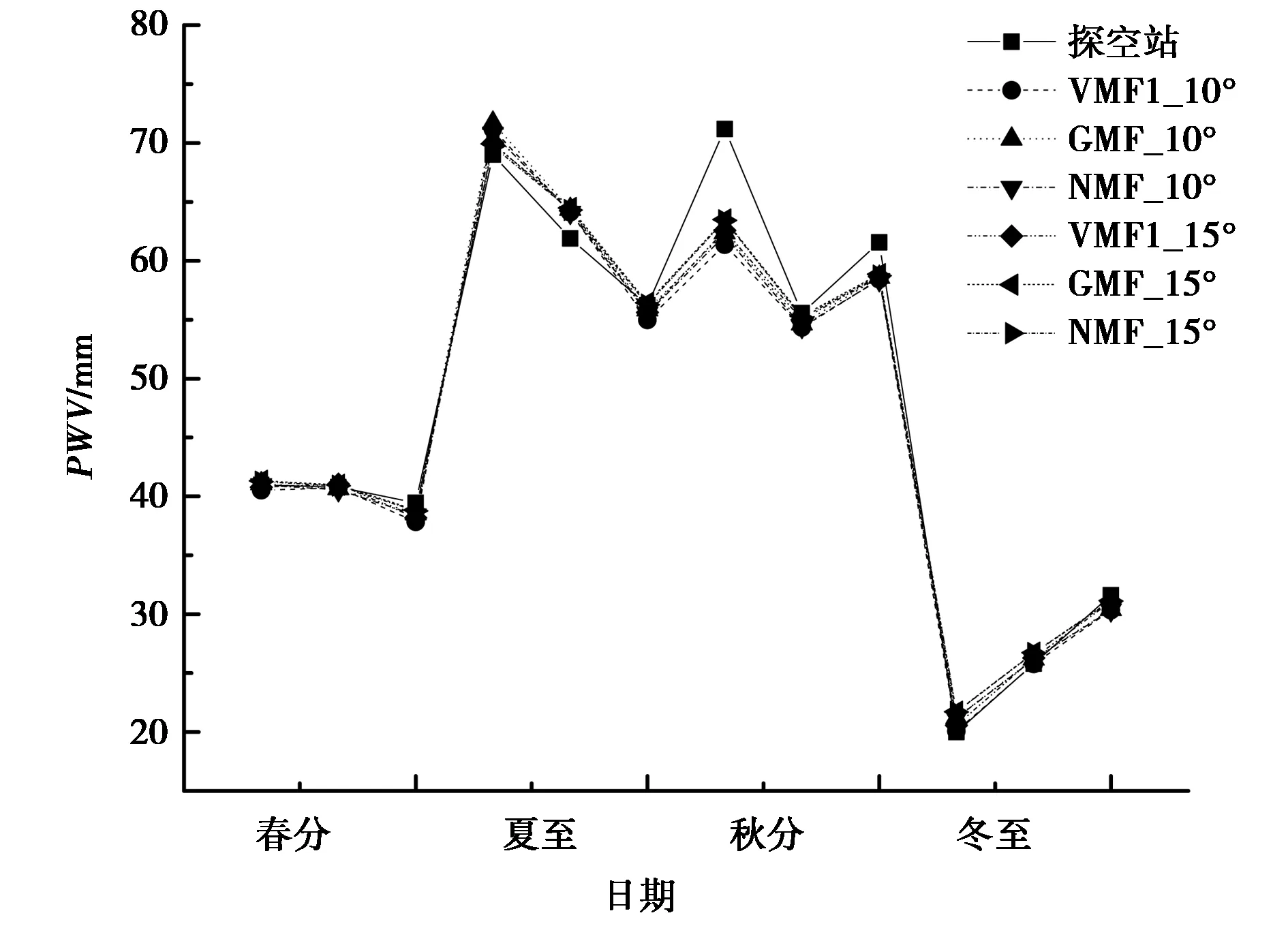
图4 HKSC站不同映射函数方案反演可降水量与探空站对比

由图3和图4可以得出:不同方案的PWV值相差很小,但在秋分日反演数据与探空站获得的PWV真值差距较大,查询香港气象网站2017-9-23的气象报告,了解到当天白天和夜间香港大部地区有雷阵雨,说明短时降雨对反演PWV精度具有较大的影响．对比图3,图4可以看出,ZTD和PWV具有很强的正相关性,随着ZTD的增大,PWV也随之增大,为缺少气象资料地区利用ZTD进行气象预报提供了参考．

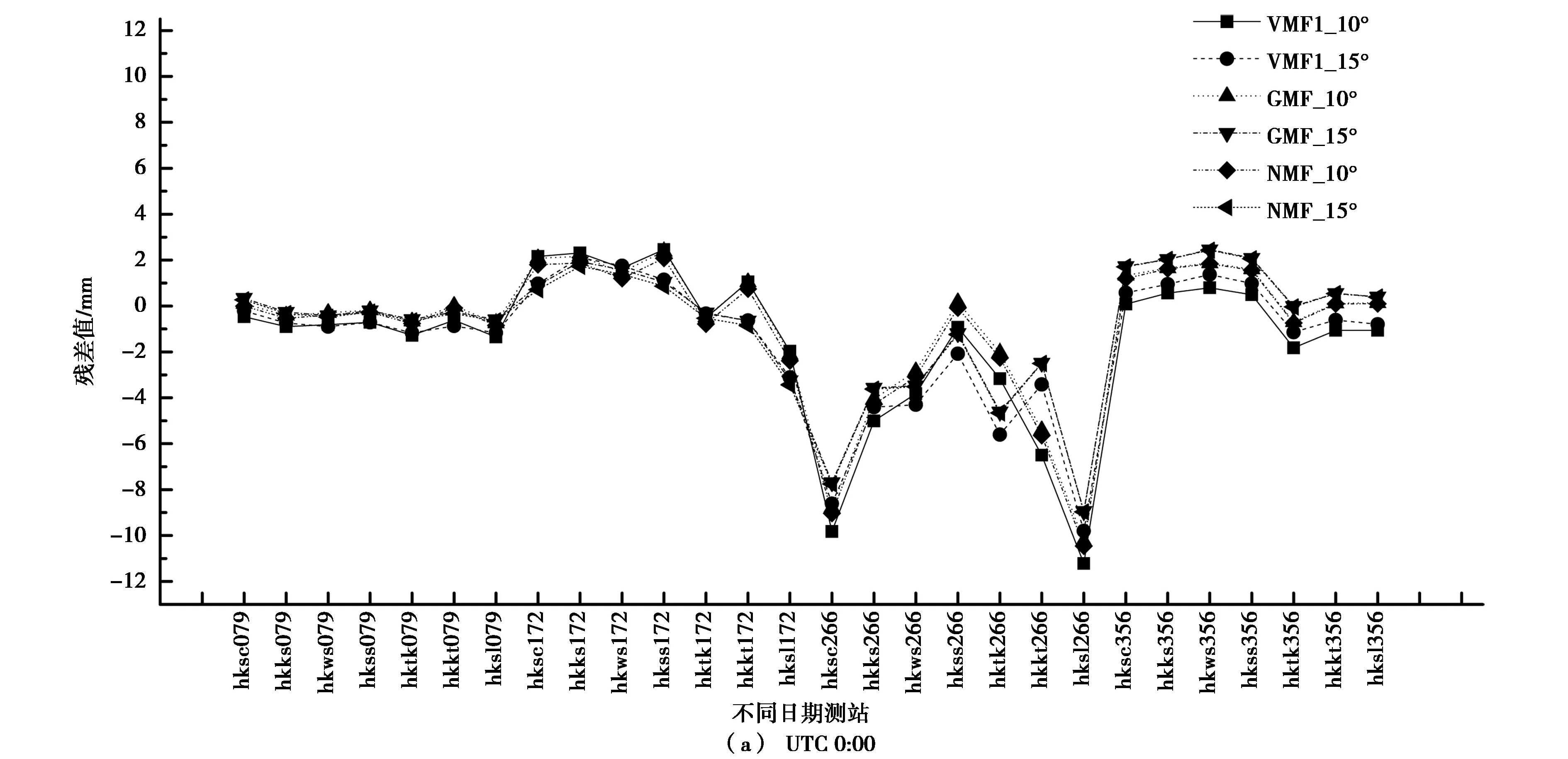
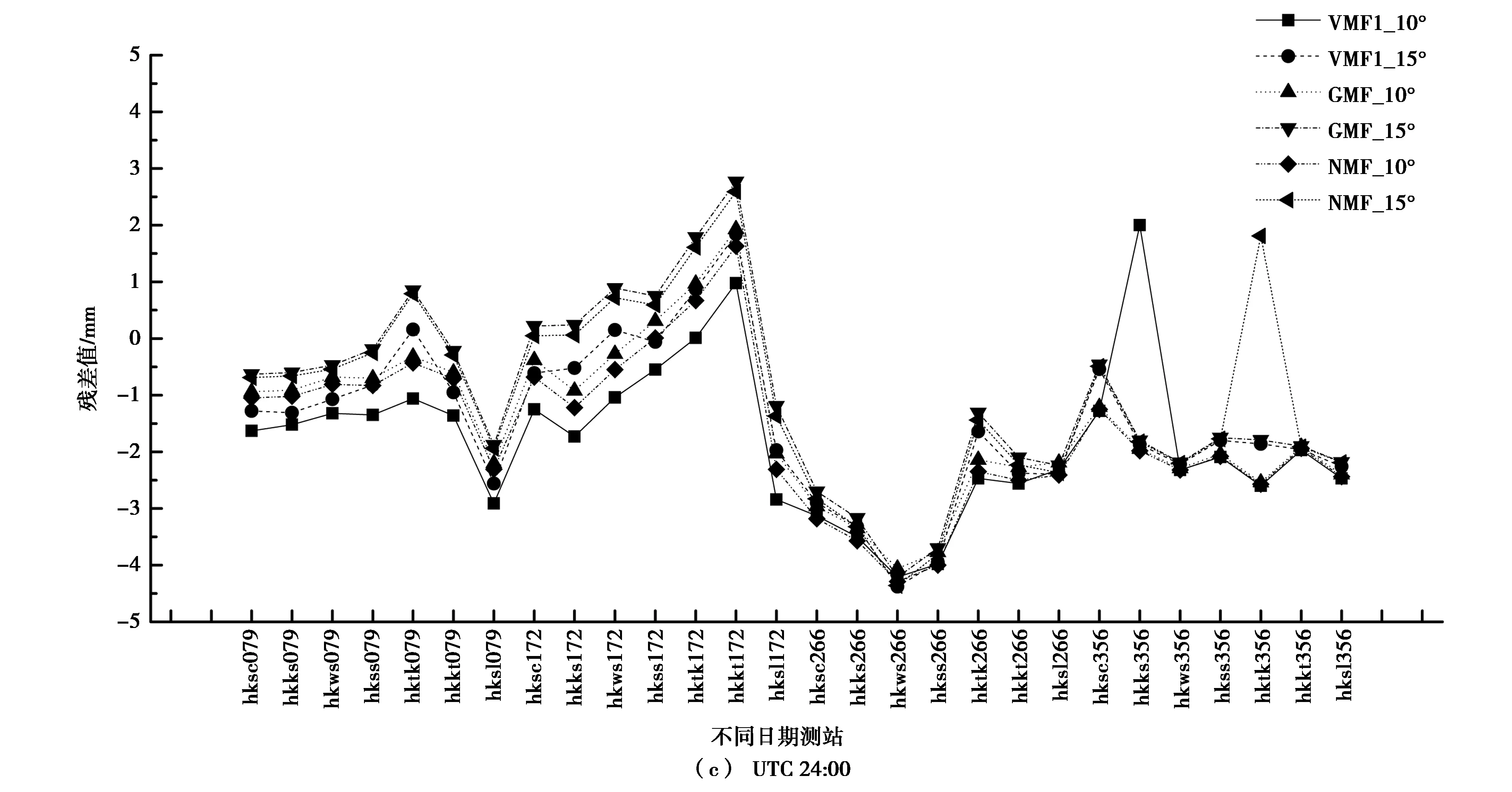
图5 不同时段测站反演PWV残差值

UTC时段VMF1-10°VMF1-15°GMF-10°GMF-15°NMF-10°NMF-15° 0:002.306 82.158 91.968 91.912 51.991 11.935 3 12:000.937 10.818 20.889 30.796 10.930 40.813 5 24:002.015 71.701 11.722 91.578 21.828 61.621 1

表5 不同解算方案反演PWV精度

从图5、表4可以看出:不同时段反演精度差别较大,其中UTC 12:00反演精度最高．相同时段GMF函数在15°高度角时反演精度最高．

分析图5、表4和表5,可以得出:

1) 相同高度角时,3种映射函数模型反演PWV其精度变化趋势基本一致,但不同季节反演精度相差较大,春分和冬至反演精度较高,而夏至和秋分反演精度较低且不同测站水汽值变化较大,说明香港地区夏至日和秋分日对流层水汽值变化剧烈且降雨较多,导致不同测站反演的PWV变化幅度和精度差别较大．

2) 不同高度角时,VMF1在10°高度角时的反演精度均低于15°高度角反演精度,初步分析可能由于高度角较低导致多路径误差增大,从而使水汽反演精度较低,比较6种解算方案的平均反演精度可以看出,GMF在15°高度角时的解算精度最高,NMF函数在不同高度角反演精度均比GMF低,VMF1反演精度最差．因此在水汽反演时,推荐使用GMF函数．

3 结束语

本文利用香港地区SatRef中7个测站以及三个IGS站在2017-3-20、2017-6-21、2017-9-23、2017-12-22共计4d数据,通过GAMIT解算,比较和分析VMF1、GMF、NMF3种映射函数在10°、15°高度角下的基线解算误差和反演PWV误差的影响,结果表明:

1)基线解算时,VMF1、GMF、NMF 3种映射函数在水平方向的误差较小,优于5 mm, 垂直方向的误差较大,最大为14.986 mm．VMF1和GMF映射函数在3个方向上的精度高于NMF映射函数,考虑GMF映射函数的连续性比VMF1函数好,所以在基线解算时推荐使用GMF函数．3种映射函数卫星高度角为10°时在N、E、U 3个方向的基线解算精度均高于卫星高度角为15°．

2)不同方案解算PWV的值相差很小,且ZTD与PWV具有很强的正相关性,可以利用ZTD与PWV的强相关性为因缺少实测气象资料而无法进行PWV反演试验的地区仅利用ZTD进行气象预报提供了参考．

3)不同季节反演PWV精度相差较大,春分和冬至反演精度较高,秋分和夏至反演精度较低且不同测站反演精度变化幅度较大,间接说明香港地区夏秋两季降雨较多且对流层水汽值变化幅度较为剧烈．

4)GMF映射函数在15°卫星高度角时反演PWV精度最高,但与GMF在10°高度角的反演精度相差不大．综合考虑基线解算和反演PWV的最佳解算方案,本文推荐在香港地区进行GNSS反演PWV试验采用GMF映射函数模型,并设置卫星高度角为10°作为解算截止高度角．