一种聚类与kNN结合的协同过滤算法

喻新潮，曾圣超，温柳英 ，罗朝广

(西南石油大学 计算机科学学院，成都 610500)

1 引 言

协同过滤[1]是推荐系统中广泛使用的技术之一，其主要的特点在于不依赖商品的内容，而是完全依赖于一组用户表示的偏好[2].协同过滤可分为两大类：基于内存[3]和基于模型[4].前者使用整个用户商品数据库进行预测，如slope one[5]，矩阵分解[6]等.后者通过学习用户偏好的描述性模型，然后将其运用于预测评分，如神经网络分类[7]，贝叶斯网络[8]等.

传统的kNN[9]推荐算法是使用所有邻居进行商品之间的相似度计算.这不仅导致其时间复杂度较高，且由于只是用单个距离度量参与相似度的计算，还会使推荐精度不理想，如Jaccard[10]，Manhattan[11]等.

本文通过结合聚类与kNN算法，提出了一种更加高效的协同过滤算法(C-kNN).首先，我们使用M-distance聚类方法[12]对数据进行预处理，旨在把具有相似性的商品归为一簇.M-distance是一种基于平均评分的聚类算法，相比k-means[13]，它具有更优的时间复杂度，且聚类的结果是确定的.然后，我们针对同一簇中的商品进行预测，其中预测评分为邻居评分的期望.C-kNN不仅通过聚类显著地缩小了邻居的搜索范围，进而有效地提高运行速度，还考虑了商品之间的强关联性，因此能够更加准确的预测出用户对商品的评分.其中，相似度的计算采用的是Manhattan距离.它把两个商品之间的评分差的绝对值作为度量衡，且距离越小越相似.

实验采用留一法(leave-one-out)[14]作为交叉验证的方法，即每次都只将单个评分作为测试集，而其余的数据用作训练集.实验数据集包括MovieLens100K，MovieLens1M，Epinions以及Netflix.对于MAE而言，C-kNN比传统的基于kNN的推荐算法在MovieLens100K上大约有4%到5%的提升，在MovieLens1M上大约有7%到10%的提升，在Epinions上大约有1%到2%的提升，在Netflix上大约有2%到16%的提升.对于RMSE而言，C-kNN比传统的基于kNN的推荐算法在MovieLens100K上大约有6%到7%的提升，在MovieLens1M上大约有7%到9%的提升，在Epinions上大约有3%到4%的提升，在Netflix上大约有1%到17%的提升.

2 相关工作

全球信息量的增长速度远超过我们可以处理的速度.每年都有很多尚未被探索的信息需要我们去处理.在如此庞大的信息量中找出我们所需要的信息是非常困难的.但是，有些技术可以帮助我们过滤没有用的信息并找到有价值的信息.其中推荐系统中的协同过滤算法是应用最成功，也是最广泛的技术之一.

协同过滤推荐是通过探索用户对商品或者信息的偏好来提取可能对该用户有用的信息.偏好的提取可以是基于用户的相似性也可以是基于商品的相似性.基于用户的相似性算法首先根据新用户的历史数据，找到与其具有相似兴趣的用户，我们称之为邻居，然后将邻居喜欢的物品推荐给新用户.基于商品的相似性算法试图找到与被推荐商品相似的一类商品，然后把它推荐给用户.然而不管是基于用户还是基于商品的推荐，都需要在全局寻找和其具有相似性的邻居，这不仅会导致时间复杂度较高，而且也会降低最终推荐的精确度.

聚类的思想对于找出商品之间的相似关系非常有用.聚类的问题可以定义为：给定d维空间中的n个数据点并将它们划分为k个簇，簇内的数据点比簇外的数据点更加相似.

基于聚类思想的推荐，丁小焕等人提出了一种基于平行因子分解的协同过滤推荐算法[15].该算法所提出的三种不同方案的推荐模型对于精确度和召回率有较高的提升.杨大鑫等人提出的基于最小方差的k-means用户聚类推荐算法[16]在缓解数据稀疏性方面具有显著的效果，且在推荐准确率上，比传统的协同过滤算法有较大的提升.

kNN是由Cover和Hart于1968年提出的一个理论上比较成熟的方法.它的基本思想是：给定新的商品后，计算新商品与所有的邻居之间的相似度，并找出k个最相似的样本.kNN算法的优点在于稳定性较好且简单易用.但由于仅使用了单一的距离度量来计算相似度，这会降低推荐的精确度.

3 问题描述

本节首先提出了商品聚类信息系统.然后，给出了评分预测问题和商品聚类信息系统问题的形式化表达.

3.1 商品聚类信息系统

定义1.一个商品聚类信息系统是一个6元组：

S=(U，T，r，R，q，W)

(1)

其中U={u0，u1，…，un-1}表示为用户的有限集合且|U|=n，T={t0，t1，…，tm-1}是商品的有限集合且|T|=m，r:U×T→R，是用户对商品的评分函数，且ri，j表示用户ui对商品tj的评分，i∈[0，n-1]，如表1所示n=5，j∈[0，m-1]，如表1所示m=5.q:T→Q是商品所属簇的映射，qj表示商品tj所属簇.

如表1所示，E=2用户u0对商品t0的评分为1，且没有评价过商品t2.

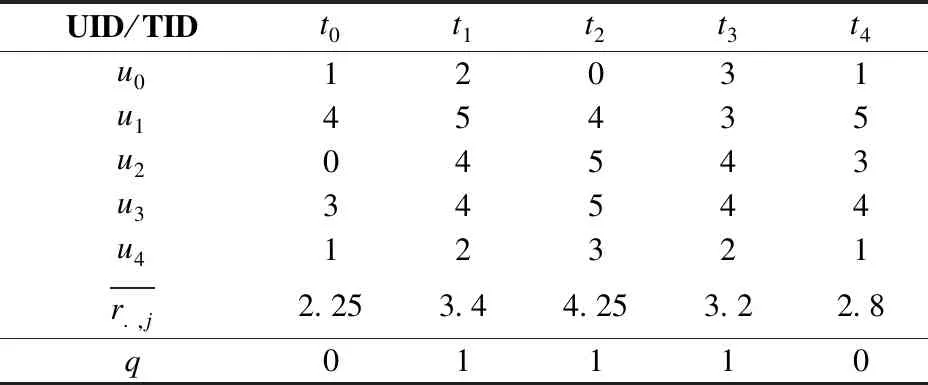
表1 商品聚类信息系统Table 1 Item clustering information system

通常，评分数据通常为5个评级，即R={ 1，2，3，4，5}.注：rij=0表示用户ui没有评价过商品tj，W={0，1，…，E-1}表示所有商品被划分为E个簇.因此，以下性质成立.

性质1.两个商品tj与tj，属于同一个簇，当且仅当

qj=qj

(2)

如表1所示：q0=q4，q1=q2=q3.其中Q所对应的集合为Q0={t0，t4}，Q1={t1，t2，t3}，Q={Q0，Q1}.

3.2 问题描述

问题1.预测评分.

1)输入：S=(U，T，r，R，q，W)；

2)输出：预测评分；

3)约束条件：当两个商品属于同一簇时，才计算它们之间的相似度；

4)优化目标：使预测的评分更加接近真实的评分.

问题2.商品聚类.

1)输入：U，T，r，R，E；

2)输出：Q；

3)约束条件：设置阈值，同属于一个阈值区间的商品被分为一簇；

4)优化目标：尽可能把相似性较强的商品划分到同一簇中.

4 C-kNN算法

本章首先描述了预处理技术，即获得聚类信息系统.其次，详细介绍本文提出的C-kNN算法.最后，用一个运行实例来提高算法的可读性.

4.1 C-kNN算法

首先我们给出C-kNN算法的框架图，如图1所示.

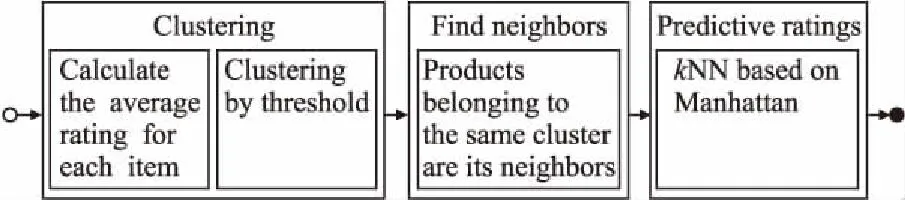
图1 算法框架Fig.1 Algorithm framework diagram

算法1描述了C-kNN的实现过程.

第1行，通过M-distance算法把商品划分到不同的簇中.

第2行，初始化邻居商品集合.

第3-11行，这是本文算法的核心.在满足两个商品同时属于一个簇(第3行)且用户ui对商品tj和tj，的评分都不为0时，通过Manhattan距离计算它们之间的相似度，公式如下：

(3)

第7，8行，每计算一个相似度就和该数组中的元素进行比较，确保NeighborDistances[.]是一个从小到大有序的数组，数组是由k个最相似的元素组成.

第12行，取相似度最高的k个商品的平均分，即用户ui对商品tj的预测评分值.

下面给出算法1的伪代码.

算法2描述了算法1(第1行)中商品聚类的具体实现过程.

第1-6行，找出评分矩阵中每个商品的平均分，其公式为：

(4)

表2 C-kNN算法Table 2 C-kNN algorithm

第7-11行，计算每个商品所属的簇的下标索引，其计算公式为：

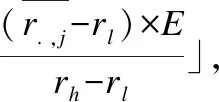
(5)

第12-14行，把每个商品分配到它所属的簇中并得到簇的集合Q.对于1≤q≤E，其所属的簇为：

(6)

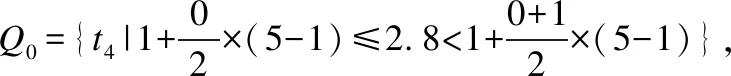
下面给出算法2的伪代码.

4.2 运行实例

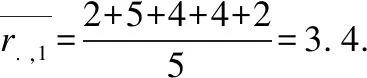
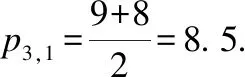
表3 聚类算法Table 3 Clustering algorithm

5 实验分析

本节首先介绍并分析实验所用的数据集，其次介绍所使用的评价指标，接着描述总体的实验设计，最后分析实验结果.

5.1 数据集

实验采用4个真实数据集，分别是Epinion、MovieLens1M(ML1M)、MovieLens100K(ML100K) 、Netflix.通过对数据集的分析可以得出，4个数据集的平均分分别是3.75，3.53，3.51和3.6.最流行的电影分别被评价2314，7359，7372和32944次.如表4所示.

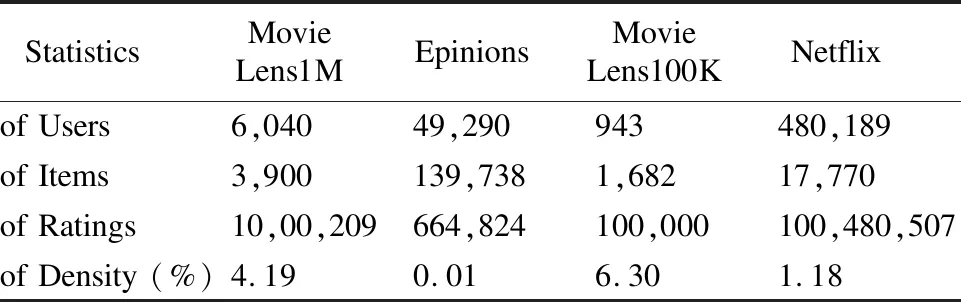
表4 数据集信息Table 4 Statistic information of dataset

5.2 评价指标

本文所采用的推荐质量评价指标是均方根误差RMSE和平均绝对误差MAE.这二个指标广泛用于评估推荐系统的性能.

RMSE是指参数估计值与参数真值之差平方的期望值的算术平方根，值越小说明预测模型描述实验数据具有更好的精确度.公式如下：

(7)

其中pi，j表示用户ui对商品tj的预测评分，ri，j表示用户ui对商品tj的实际评分.

MAE则能更好地反映预测值误差的实际情况，值越低说明误差越小.其定义为：

(8)

其中pi，j，ri，j表示与公式(7)相同.

5.3 实验设计

在本节中，我们旨在讨论以下两方面：

1)不同的聚类结果对推荐准确性的影响.

2)算法C-kNN与经典kNN的性能对比.

针对第1)方面，对用户进行聚类时，我们尝试使用多种进行聚类以找出不同的聚类结果对实验结果的影响.

针对第2)方面，我们设置k的值为5.根据找出的合适大小的平均分聚类在5.2所提出的二个指标上来进行实验，随后分析结果并比较算法的差别.

由于算法的运行时间较长，我们把ML1M的数据集取其中的3部分分别进行实验，分别为：用户评分次数大于500，并小于600(ML1M_1)；用户评分次数大于500，并小于700(ML1M_2)； 用户评分次数大于300，并小于400(ML1M_3).数据详细信息如表5所示.

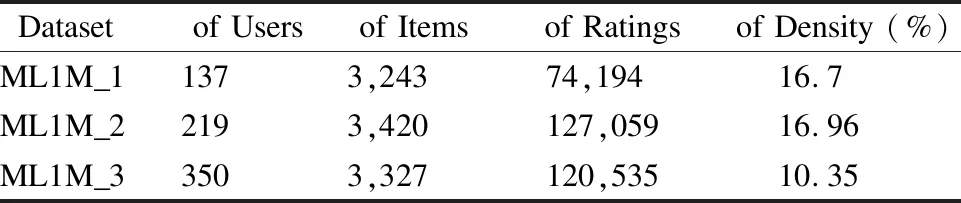
表5 数据集信息Table 5 Statistic information of dataset

由于Netflix数据集比较大，我们取其中的五部分进行实验，分别为：用户评分次数大于35，并小于40 (NF_1)； 用户评分次数大于31，并小于34 (NF_2)； 用户评分次数大于395，并小于400 (NF_3) ；用户评分次数大于2300，并小于2350 (NF_4)； 用户评分次数大于3500，并小于4000(NF_5).数据详细信息如表6所示.

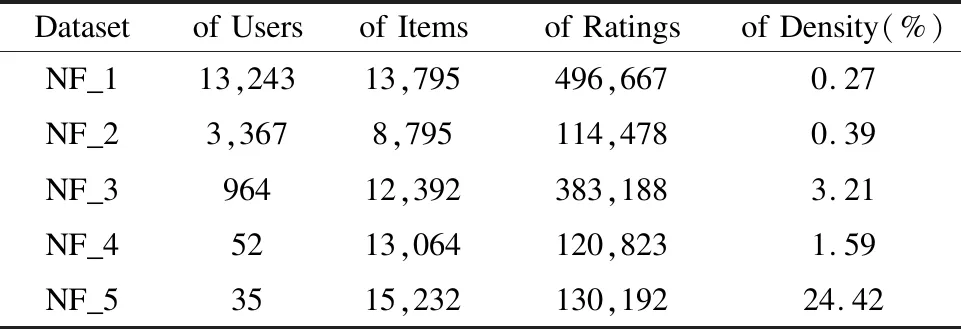
表6 数据集信息 Table 6 Statistic information of dataset

5.4 实验结果

按照4.3节的实验设计，分别在三个真实的数据集上进行实验.

方面1，在MovieLens100K上进行实验，找出不同的聚类对实验结果的影响.根据聚类阈值的大小，我们将商品分为2到10组.结果如下：

由图2和图3可以得出，不同的阈值会影响实验结果.因为根据不同的，可能导致有些较为相似的邻居没有被聚到同一簇中.

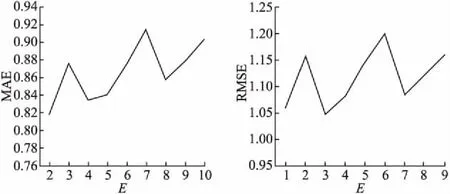
图2 E的选择对MAE的影响Fig.2 Influence of E′s choice on MAE图3 E°的选择对RMSE的影响Fig.3 Influence of E′s choice on RMSE

方面2，分别测试了RMSE，MAE两种评价指标.结果如下：

表7 MovieLens100K实验结果(MAE)Table 7 MovieLens100K experimental results (MAE)

通过实验可以知道，C-kNN比经典的kNN推荐算法在MovieLens100K上，性能大约有4%到5%的提升，在Epinions上大约有1%到2%的提升.

表8 MovieLens100K实验结果(RMSE)Table 8 MovieLens100K experimental results(RMSE)

由表8可知在MovieLens100K、Epinions上，C-kNN比经典的kNN推荐算法在RMSE上分别提升了6.34%、3.55%.

表9 ML1M实验结果(MAE)Table 9 ML1M experimental results(MAE)

由表9得到的信息，在ML1M上划分成的三个子数据集分别做了实验.结果表明，相较于经典的kNN协同过滤算法，预测值误差降低了7%到10%.

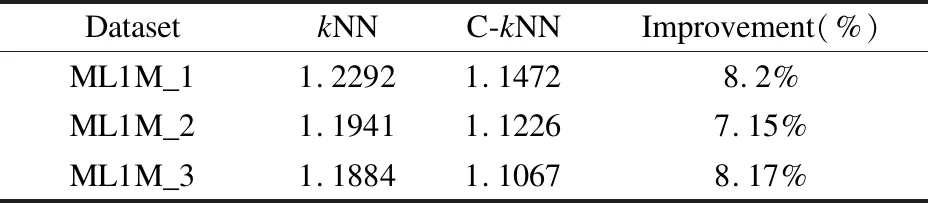
表10 ML1M实验结果(RMSE) Table 10 ML1M experimental results(RMSE)

根据表10结果表明，C-kNN与经典的kNN推荐算法对比，在ML1M所划分的三个子数据集中在RMSE上提升了7%到9%.

表11 Netflix实验结果(MAE) Table 11 Netflix experimental results(MAE)

根据表11实验结果表明，在不同的稀疏度下，C-kNN比经典的kNN推荐算法在MAE上都有较大的提升.

表12 Netflix实验结果(RMSE) Table 12 Netflix experimental results(RMSE)

如表12所示，C-kNN协同过滤算法在不同稀疏度的下都要比经典的kNN算法在RMSE上均有较大的提升.

6 结 语

本文提出了一种聚类与kNN结合的协同过滤算法，并在4个真实数据集上进行了实验.其性能相比于传统的kNN推荐算法，在MAE和RMSE上都有较大的提升.表明在使用kNN算法进行评分预测前，利用M-distance聚类算法对所有商品进行划分，最终可以有效的提高推荐精度.