基于正交基神经网络的火灾探测器及报警系统的可靠性研究

王 静,裴迎公

(1.安徽新华学院,安徽 合肥 230088;2.安徽威尔信通信科技有限责任公司,安徽 合肥 230088)

0 引言

火灾探测器及报警系统(即火灾探测报警系统)包括火灾探测器及火灾探测报警系统两个部分,其在火灾早期的探测中起到非常重要的作用。但是实践证明,由于可靠性问题导致的系统故障,也会不同程度地造成人员伤亡和财产损失。因此,火灾探测器及报警系统的可靠性引起了人们的关注和研究[1]。

对火灾探测报警系统的可靠性用科学且有效的方法进行研究和分析,探究其可靠性随着使用寿命产生的一系列变化规律,为火灾探测报警系统的维修和管理提供理论基础,从而减小或避免在火灾中产生的人员伤亡及财产损失[2]。

1 正交基神经网络

人工神经网络(Artificial Neural Network，ANN)是一种模仿人脑结构及其功能的脑式智能信息处理系统,是对人脑或自然神经网络的若干基本特性的抽象和模拟。其基本特点是信息处理的并行性、信息存储的分布性、信息处理单元的互连性、结构的可塑性、高度的非线性、良好的容错性、计算的非精确性和自学习、自组织与自适应性,基本功能是联想记忆、非线性映射、分类与识别、优化计算和知识处理。

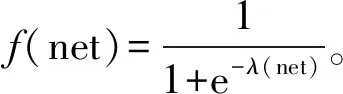
由于BP神经网络在实际应用中存在着局部极小和收敛速度缓慢等问题。在本文中,将一组正交基函数用于隐层神经元的激活函数,各隐层单元的加权和为Sigmoid函数的输入。正交基神经网络主要采用BP误差反向传播算法对权重进行修改。网络结构简单、网络参数较少、网络的训练速度较快是正交基神经网络主要优点[3]。同时,因为每个隐层神经元的激活函数是不

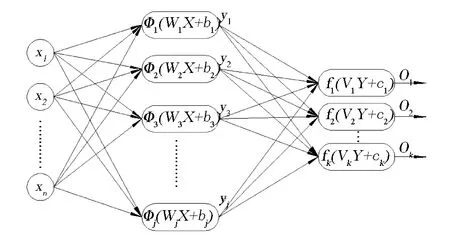
图1 正交基神经网络图Fig.1 Orthogonal basis neural network diagram

同的,这使得它更接近生物神经元,能够有效地提高网络的收敛性能。正交基神经网络设计如图1所示。

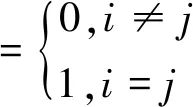
(1)

即函数序列两两正交。

在网络学习训练的过程中,假设包含的总训练样本数为P,现从中选取第N个样本对网络训练,设以xi、yi、Ok依次分别表示输入节点、隐节点和输出层节点;其中,隐节点、输入节点两者之间的连接权值定义为Wji,阈值定义为θj,输出节点、隐节点两者之间的连接权值定义为Wkj,阈值定义为θj;输出节点的期望值定义为tk。针对选取的第N个样本,用E(N)表示实际的输出值Ok和期望的输出值tk的误差,可用E表示,算法的实现和具体的公式推导如下：

隐节点的输出:

(2)

输出节点的计算输出:

(3)

输出节点的误差公式:

(4)

权值的修改方法输出节点：

(5)

其中E是多个Ok的函数,但只有一个Ok与wkj有关,且各Ot之间是相互独立的,可得

(6)

(7)

则

(8)

其中f′(netk)为输出函数的导数。

(9)

隐层节点：

(10)

其中

(11)

(12)

(13)

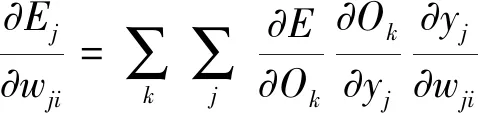
(14)

其中Φj′(netj)为隐层函数的导数。

(15)

为使误差函数E沿着负梯度方向下降,权值Δwkj、Δwji进行如下修正:

(16)

(17)

η为学习速率;则修正后的权值为:

wkj(t+1)=wkj(t)+Δwkj(t)+αΔwkj(t-1)

(18)

wji(t+1)=wji(t)+Δwji(t)+αΔwji(t-1)

(19)

其中t为学习循环或学习次数,α为动量因子。

将隐层节点和输出层节点各加一个输入维,新添加的输入维的值恒为-1,然后此新加入的维所对应的权重即为对应的域值,则此域值的校正方法与权重的校正方法相同。

对第N个样本,E(N)为实际的输出值Ok与期望的输出值tk之间的误差,Eall为所有训练样本总的误差。

(20)

2 系统的可靠性神经网络预测与分析

2.1 数据样本

所有火灾探测器一共发生的故障次数为320次,部分故障时间表如表1所示。

表1 火灾探测器部分故障时间表Table 1 Partial failure schedule of fire detectors

火灾探测报警系统的故障次数为1568次,部分故障时间表如表2所示。以系统记录的故障数据作为研究对象,对火灾探测报警系统的故障数据进行分析。

表2 火灾探测报警系统部分故障时间表Table 2 Partial failure schedule of fire detection and alarm system

2.2 火灾探测器的可靠性神经网络预测

设置学习率为0.005,动量为0.7,神经网络的输入为火灾探测器的可靠性的时间序列,其期望输出值为网络经训练获取的可靠性数据[4]。图2显示进行4000次训练后的正交基神经网络的函数逼近情况。其中,前期经统计和威布尔拟合的数据用虚线表示,正交基神经网络的模拟输出结果用实线表示。图3为误差曲线,在500次训练后基本保持不变。

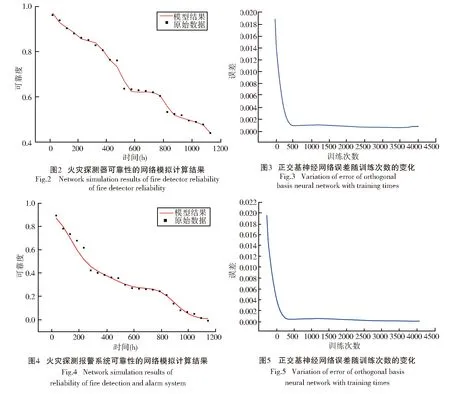
可靠性随时间的预测结果(设为R1(t))可以通过训练后的神经网络模型得到[5],计算故障间隔时间MTBF

(21)

2.3 火灾探测报警系统的可靠性神经网络预测

设置学习率为0.01,动量为0.6,神经网络的输入为火灾探测报警系统的可靠性的时间序列,其期望输出值为网络经训练获取的可靠性数据。图4显示进行4000次训练后的正交基神经网络的函数逼近情况。其中,前期经统计和威布尔拟合的数据用虚线表示,正交基神经网络的模拟输出结果用实线表示,可以看到两条曲线基本重合。图5为误差曲线,在500次训练后基本保持不变。

可靠性随时间的预测结果(设为R1(t))可以通过训练后的神经网络模型得到,计算故障间隔时间MTBF

(22)

通过正交基神经网络预测出的火灾探测器以及火灾探测报警系统的可靠性结果同前期通过复杂计算而得到的结果相差较小。因此,这种方法在一定程度上是可行的。基于正交基神经网络的方法,对故障数据的可靠性序列随时间的变化进行逼近,并基于逼近的结果计算出系统平均故障间隔时间,从而避免了可靠性假设与复杂的数学计算。

3 结语