基于Petri网的模拟训练评估模型及算法*

邱 涛，赵旭东，席建民，谢瑞云

（中国电子科技集团公司第三十研究所，四川 成都 610041）

0 引 言

模拟训练的主要目的是通过反复操作，使参训人员能够熟练掌握使用流程和规则，提高装备使用效率。如何评估模拟训练的成效一直是模拟训练面临的难点问题，其根本原因在于不同的模拟训练科目，缺乏标准的评估模型，很难利用统一的评估指标体系进行评估，从而造成不同评估模型需要采用不同的评估算法[1-5]。

本文主要聚焦研究针对软件类装备的模拟训练评估模型和算法，提出了统一的模拟训练评估模型，构建了简化的评估指标体系，并提出了一种低复杂度的模拟训练评估算法，该算法采用了分层加权求和的思路对模拟训练结果的进行评估，为了提升算法的准确性，该方法还利用了半监督学习方式不断优化不同评估指标以及不同操作的权重值，以获得最优的模拟训练评估参数。所提模型和算法在保证评估结果准确性的基础上，其计算复杂度较低，而且能够给出训练出错的具体原因，为提高后续模拟训练成效提供有力的参考。

1 模拟训练评估模型

1.1 Petri网简介

Petri网是一种图形及数学建模工具，能较好地描述系统的结构，表示系统中的并发、同步、冲突与顺序等关系，并以图形表示的组合模型具有直观、易懂和易用的优点，对描述并发现象有它独到的优越之处。同时，Petri网又是严格定义的数学对象，有完善的数学理论基础。

Petri网可以描述为一个五元组，即PN={P,T,F,W,M0}，其中P表示库所，P={P1,P2,…,Pn}，n为 库 所 个 数，T表 示 变 迁，T={T1,T2,…,Tm}，m为变迁个数，F∶P×T∪T×P是转移函数，表示从库所到变迁的弧和从变迁到库所的弧，W∶F→{1,2,…}是权重函数，M0∶P→{0,1,2,…}是初始标识。

1.2 基于Petri网的模拟训练评估模型

模拟训练的主要目的是通过反复操作，使参训人员能够熟练掌握使用流程和规则，提高装备使用效率。模拟训练过程是一个离散事件过程，Petri网非常适合应用于该场景。利用Petri网对模拟训练系统进行建模实际就是对操作流程的建模。不同的模拟训练装备，会有不同的操作流程，所以需要利用Petri网对不同模拟训练系统进行统一的建模[6]。

传统装备模拟训练大部分以实物训练为主，随着软件在装备中扮演着越来越重要的角色，软件类装备模拟训练成为模拟训练的重要组成部分。相比于实物装备操作来说，软件类装备的操作大多都是通过复杂的人机交互界面完成。Petri网的众多优点使其非常适用于模拟复杂的人机界面交互过程。

软件操作通常由两个部分组成，软件界面和界面上的按钮，通过点击界面上不同的按钮实现在不同操作界面之间切换。Petri网非常适用于描述这种场景，可以将这种软件操作过程描述为一个简单的四元组Petri网，PN={P,T,F,W}，其中P表示系统状态，对应于软件操作的每个界面，T表示每个软件界面的操作按钮，F表示界面和操作按钮之间的关系，W是与操作相对应的权重，用于表示不同操作在整个软件模拟训练评估中的重要程度。如果某个软件非常复杂，还可以软件建模成由多个子Petri网组成的总Petri网。

将软件模拟训练建模成Petri网模型之后，可以利用Petri网理论，判断软件操作是否存在死循环，而且能够验证软件操作的可达性，保证每个操作或者一系列操作的操作结果都在固定的集合中，为设计模拟训练评估算法提供重要的理论基础。

2 模拟训练评估算法

构建了模拟训练评估模型之后，需要着重研究模拟训练评估算法，能够对模拟训练进行定量评估，并且能够准确指出作战人员对于软件装备的操作问题，为作战人员熟练掌握软件装备的操作提供有力支撑。

通常模拟训练评估的方法有两种类型，一种是通过构建评估指标体系，采集不同评估指标的执行情况，然后利用加权求和的方法计算最后的评估结果；另一种则是定义标准操作，通过计算实际操作与标准操作之间的相似度给出最后的评估结果。第一种方法的计算复杂度低，但很难保证评估指标体系的完备性，第二种方法能够给出准确的评估，但计算复杂度过高，与标准操作步骤数量的阶乘成正比。为了充分利用这两种方法的优点，本文提出了一种全新的模拟训练评估算法，该方法通过定义一种极简的评估指标体系，利用低复杂度的评估算法完成模拟训练评估。

2.1 评估指标体系

评估指标体系是由具有相互关系的若干个 评估指标组合而成的，各指标之间相互联系、相互影响，而且指标体系具有树状层次结构，层次越低，指标越具体、越明确[7]。但为了构建一个完备、清晰的装备训练评估指标体系是一项很困难的工作。因此，本文提出了一种极简的评估指标体系，仅仅定义了三种与操作直接相关的评估指标，即操作时间、操作过程和操作结果三大类，如图1所示。

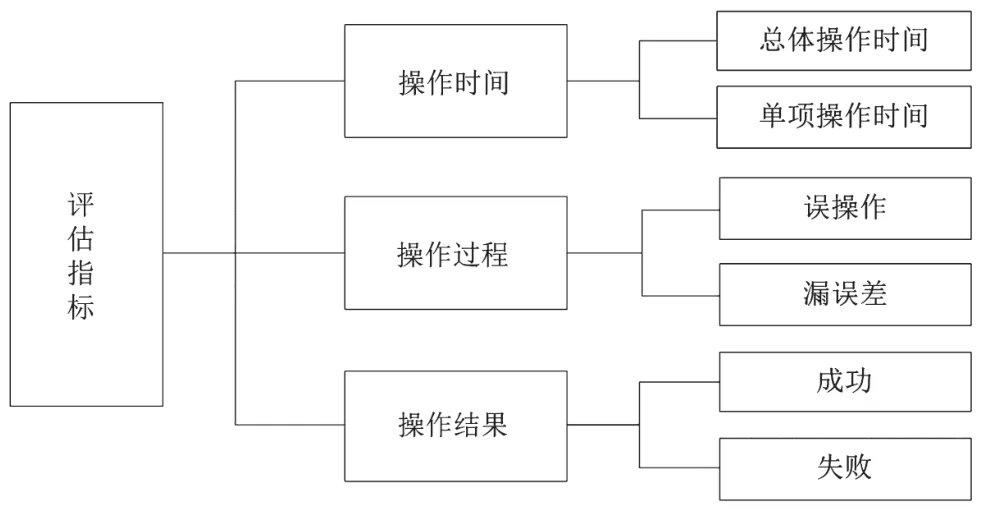
图1 评估指标体系

操作时间直接反映了模拟训练人员对于软件操作的熟悉程度，操作过程主要反映模拟训练人员是否存在误操作、漏操作或者重复操作的情况，操作结果与具体的训练科目相关，能够反映操作过程中设置的参数对操作结果影响程度。

2.2 评估指标定量表示及归一化

基于定义的评估指标体系，需要针对每个单项指标进行量化，为了使不同指标有相同的量纲，还需要对指标进行归一化。

对于操作时间，记录操作开始时间Ts和操作结束时间Te，实际的操作时间T即可表示为T=Te-Ts。定义一个操作时间门限值Tth，则操作时间T对应的评分St可以表示为：

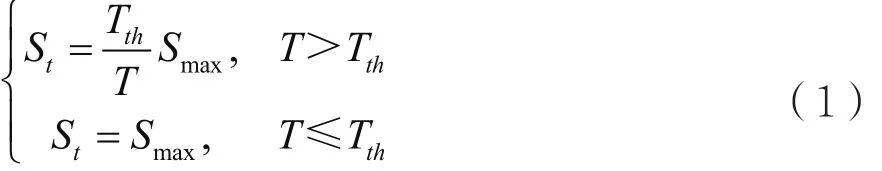
在式（1）中，Smax表示最高得分，可以根据实际情况而定。从式（1）可以看出，操作时间越长，得分呈下降趋势，当操作时间超过门限值Tth，得分随着时间增长线性下降，而当操作时间低于门限值，均认为能够获得最高得分Smax。

对于操作过程，首先需要定义总操作集合O，O由软件界面中所有能够执行的操作组成，假设N=|O|，表示软件的总操作步骤数，定义标准操作集，表示为SO。通常每个训练科目可能会有多个不同的标准操作，因此SO可以表示为一个集合，SO={SO1,SO2,…,SOJ}，j=1,2,…,J，J表示标准操作数量，对应每种标准操作j，其操作步骤数表示为N。定义权重向量Wo={w1,w2,…,wN}，如果操作步骤 i∈ SOj，则 wj＞0，且满足：

否则wi≤0，表示误操作。

最后，记录每次实际操作集合PO，记录每个操作步骤i在PO中出现的次数，并表示为向量Co={c1,c2,…,cN}，对应于每个操作步骤的执行次数。因此对于每次实际操作，操作过程评分So可以表示为：

这种操作过程的评分方式可以有效处理训练科目存在多种不同的标准操作或者某个操作存在可替代操作的情况，提供准确的评分。

对于操作结果，最简单的记录实际操作是否成功，表示为R。当操作失败，R=0；当操作成功，R=1。则操作结果评分Sr可以表示为：

从式（4）可以看出，Sr，So和Sr的取值区间均在区间[0,Smax]，实现了评估指标的定量及归一化的统一表征。

2.3 低复杂度的模拟评估算法

一种最为直接的评估算法可以描述为每个评估指标分数的加权和，即综合得分S可以表示为：

其中，St，So和Sr分别表示为操作时间、操作过程和操作结果的评分，wt，wo和wr表示各评估指标占总评分的权重，满足条件wt+wo+wr=1，因此S的取值范围[0,Smax]。

模拟训练评估算法的关键就是要准确计算训练参数W=[wt,wo,wr]以及参数WO={w1,w2,…,wN}。本文将采用一种低复杂度的模拟训练评估算法，该算法采用了分层加权求和的思路对模拟训练结果的进行评估，为了提升算法的准确性，该方法还利用了半监督学习方式不断优化不同评估指标以及不同操作的权重值，以获得最优的模拟训练评估参数。

首先，生成训练样本集TS，对于每个样本i，TSi由实际操作集合PO和对应专家评分S组成。PO表示样本i的实际操作步骤集合，Si表示综合评分，S表示对应这次操作的详细评分，由三部分组成[S,S,S]，S表示+操作时间评分，S表示操作过程评分，S表示操作结果评分。S可以根据记录的Ti利用式（1）计算而来，S可以根据最终结果利用式（4）计算而来，Si和S必须由行业专家进行评分。为了保证算法的准确性，训练样本越多越好，但是越多的训练样本意味着更高成本。因此，能够利用越少训练样本达到目标准确性凸显其重要性，假设训练样本数量表示为NTS。

然后，基于训练样本集TS，形成两个方程组：

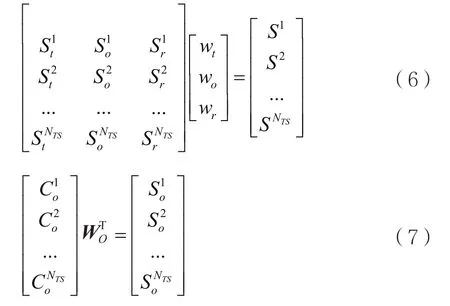
最后，基于方程（6）和方程（7），计算W和Wo。

对于W的计算，由于训练样本数量NTS＞＞|W|，|W|=3，表示集合W的势。因此，方程（6）属于超定方程，通常可以采用最小二乘法进行求解。

对于Wo的计算，由于训练样本数量NTS＜N，方程属于欠定方程，存在无数可行解。但是只要方程满足以下两个条件，稀疏性和欠采样性，就可以利用压缩感知技术[8]将问题转换为普通的线性规划问题进行求解，可以大大减少所需训练样本的数量，降低算法复杂度。

（1）稀疏性：对于某种训练情况（也可以成为某个训练科目），矢量Wo中等于0或者约等于0的元素为大多数，则称矢量Wo为稀疏的，假设假设不等于0的元素个数为λ，则矢量Wo称为λ-稀疏；

（2）欠采样性：假设训练样本数量为NTS，如果NTS＜＜N，则欠定方程具备欠采样性。

对于某个训练科目，只有对应于标准操作的权重值不为0且较大，而其他操作的权重值很小，而且|SOj|＜＜|O|，因此满足稀疏性。此外，由于训练样本数NTS＜＜N，满足欠采样性。因此，欠定方程可以转换为线性规划问题，可以表示为：

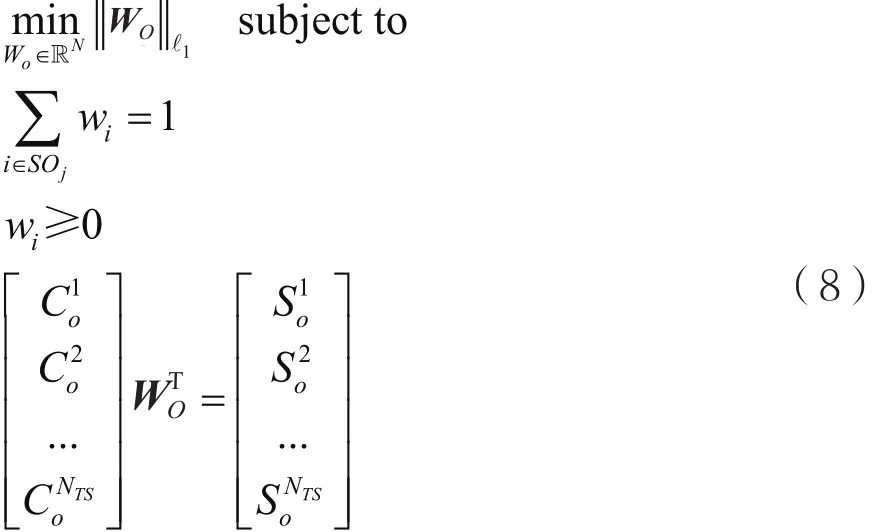
优化问题（8）可以采用经典方法求解，比如改进单纯形法、对偶单纯形法、原始对偶方法、分解算法等。

3 实验数据及分析

本文依托前期开发的“某型模拟训练评估系统”开展相关模型和算法的验证工作，该系统的总操作步骤数N约为1 000左右，涉及的训练科目多达35个。

评分误差是评估算法优劣的一个非常重要的指标，由于不同训练科目的评估相互独立，所以本文选择其中一个训练科目进行实验数据的搜集与分析。选择的科目存在3种标准操作，即J=3，每种标准操作的步骤数大约为30，即NjSO=30；采集了100个训练样本，即NTS=100。因此，对于W的求解，由于NTS＞＞|W|，属于超定方程求解，可以利用最小二乘法进行求解，本文直接利用MATLAB的库函数lsqlin（）进行求解。对于Wo的求解，满足稀疏性（NjSO＜＜N）和欠采样性（NTS＜＜N），因此可以利用压缩感知方法将其转化为普通的线性规划问题，本文直接利用MATLAB的库函数linprog()进行求解。

关于本文提出模拟训练评估算法的评分误差如图2所示，描述的是与专家评分之间的方差，此处的Smax=100。从图2中可以看出，随着样本数不断增加，评分误差逐渐缩小，当样本数小于60，评分误差与样本数量的关系密切，而当样本数大于或者等于60，评分误差在5分以内，而且通过单纯增加样本数很难再大幅提升整体的评估性能，这与压缩感知理论相符合。

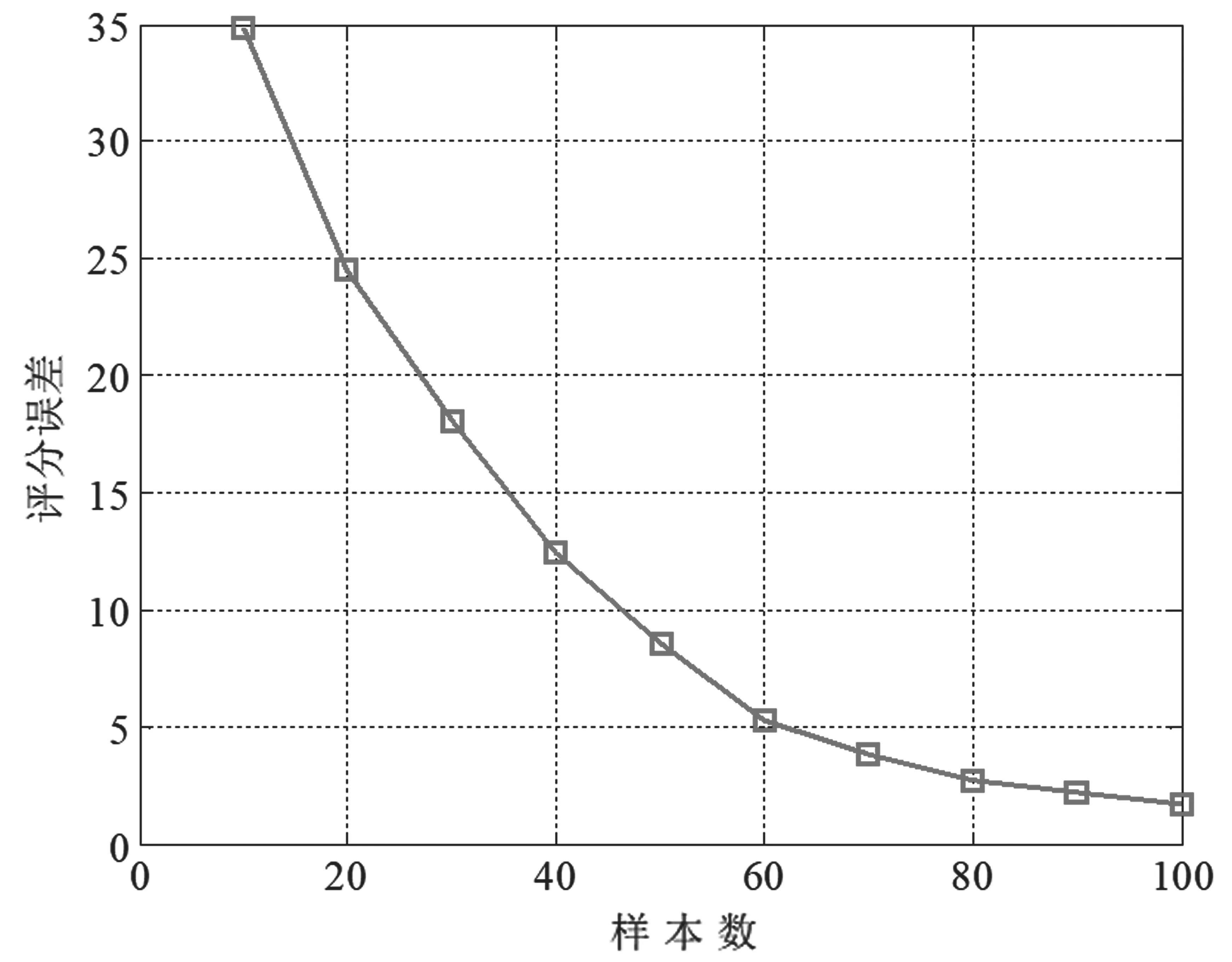
图2 评分误差

关于本文提出模拟训练评估算法与参考文献[9]提出算法的评分误差比较如图3所示，此处选取了5个训练科目进行对比。从图3中可以看出，所提算法的评分误差要高于文献[9]提出的算法，但之间的差距很小，主要是因为文献[9]的算法复杂度更高，需要对比实际操作与标准操作的每一步操作，其复杂度为O(N!)，与总操作步骤数的阶乘成正比，而本文提出算法的复杂仅为O(N2)。

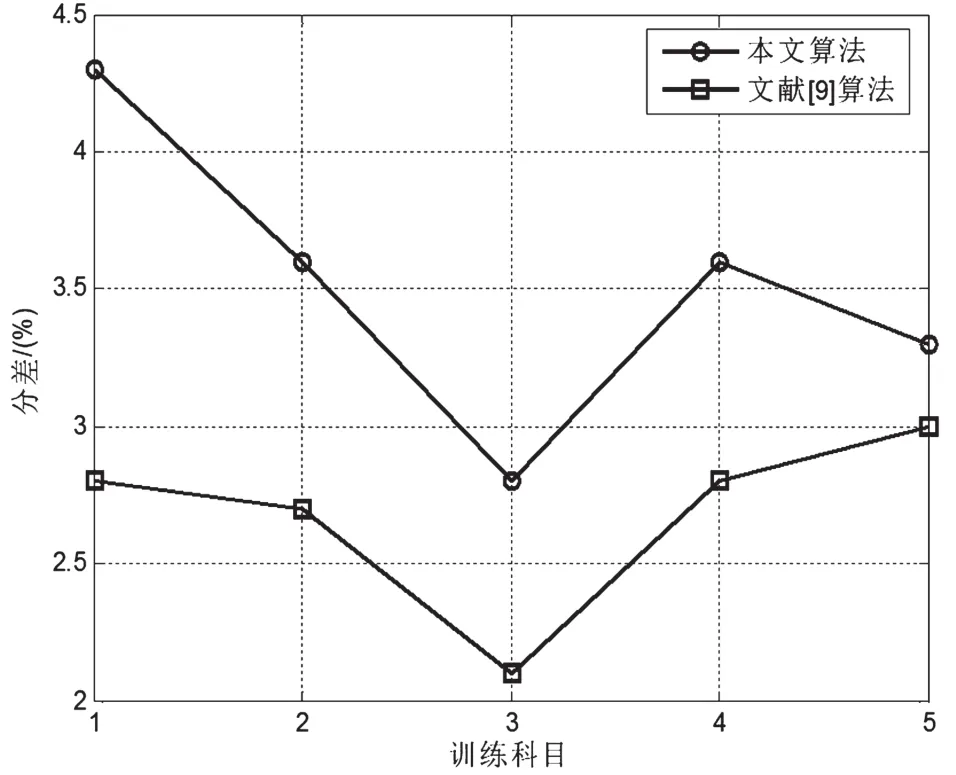
图3 不同训练科目评分误差对比

4 结 语

本文提出了一种基于Petri网的模拟训练评估模型，采用极简的评估指标体系，利用分层的加权求和方法评估模拟训练的情况，所提算法在保证评估准确性基础上，大大降低了运算复杂度，后续研究可以在此基础上进一步利用半监督学习方法不断优化不同评估指标以及不同操作的权重值，以获得最优的模拟训练评估参数。