基于仿真数据的测试性验证序贯设计方案

赵学远，王康，秦亮，王帅磊

（海军航空大学，山东烟台264001）

良好的测试性设计能保证装备系统能够在特定环境下正常工作，并且有利于缩短故障检测和隔离时间，进而实现装备系统维修保障任务精、准、快的目的[1]。

现有国内外的相关标准和文献都强调了运用基于故障注入的验证试验方法来对装备测试性设计水平进行考查[2-4]。然而，由于故障注入试验具备破坏性，对装备所有故障模式进行故障注入是不切实际的，必须依据统计试验理论确定满足要求的测试性验证试验所需的故障样本量[5-7]，然后通过故障样本量分配实施故障注入，以此检验装备测试性水平。

为对装备系统的测试性指标如故障检测率（FDR）和故障隔离率（FIR）进行评估，通常采用测试性验证的方式，即向装备的测试性样机中人工注入故障，并依据故障检测/隔离情况做出判决[3]。一个完整的测试性验证试验过程包括故障样本量确定、样本量分配、故障模式选取、故障注入、数据分析以及决策。其中，故障样本量确定是测试性验证试验的核心环节。基于故障注入试验的结果通常为成败型数据，所以选用二项分布模型对数据进行分析。现有故障样本量确定大多采用经典验证方法，即单次抽样方法，即在承制方和生产方测试性水平、风险的约束下，寻求一个最佳的故障样本量n和最大允许检测/隔离失败次数c来同时满足双方约束条件。

当前，各国针对测试性验证制定了有关标准，研究人员也针对测试性验证问题进行了一系列的研究[8-11]。田仲和石君友对测试性建模和验证的流程进行了介绍[3]，李天梅等在针对某型飞行控制系统的测试性验证试验中阐述了完整的试验方法和流程[8-11]。

随着测试性技术发展和功能需求的提升，装备系统结构越来与复杂，造价日益昂贵。因此，采用传统的样本量确定方法会增加测试性验证试验费用，甚至会对装备造成难以挽回的破坏[11]，故须要研究一种新的测试性验证方法用以减少实际样本量。

A Wald提出了一种序贯概率比检验（SPRT）方法[12-13]，并证明了该方法所需要的平均样本量比固定样本量的单次、二次及多次抽样方法均要少，且对于缩短验证周期具备明显作用。基于SPRT方法的这种优势，研究人员在此基础上将SPRT方法应用于不同的统计分布模型当中[14-16]。文献[17]利用SPRT检测和识别核电站和飞行器的故障。文献[18-19]利用了SPRT检测的齿轮裂纹。文献[20]也对SPRT进行了研究，并利用Bayes理论进行了改进。

综上所述，结合SPRT方法的优点，本文给出了基于SPRT方法的某型装备控制系统的测试性验证试验序贯试验设计方案。具体包括判决准则、阈值计算方法、截尾准则以及序贯试验方案下样本量分配和故障模式选取方法4个方面的内容。

1 基础知识介绍

1.1 约束参数

1）承制方为确保装备测试性水平能以较高概率通过验证试验的要求值p0。

2）使用方规定的装备测试性水平的下限值p1，且满足p0＞p1。

3）装备测试性水平为p0时，未能通过验证的概率，记为承制方风险α。

4）装备测试性水平为p1时，通过验证试验的概率，记为使用方风险β。

1.2 经典测试性验证方法

定义N为故障注入次数，C为最大允许检测/隔离失败次数，y是实际的失败次数。对于试验方案(N,C)，其满足：

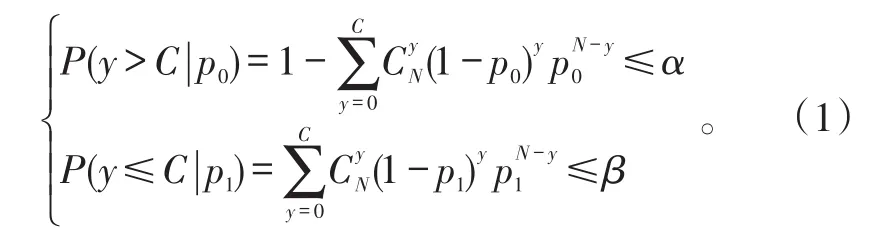
在N次故障注入试验后，试验通过要求y≤C；如果y＞C，则判定试验失败。

1.3 测试性验证序贯设计

为制定测试性验证序贯设计方案，作如下假设：

每次注入试验完成后，设当前故障注入总次数为n，当前累计失败检测次数为c，可得当前2种假设的似然概率比的对数为：

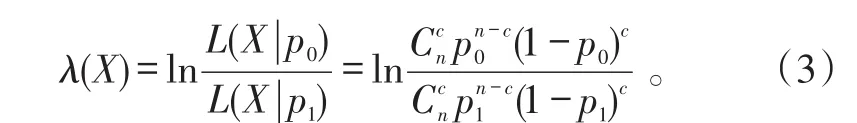
式（3）中，X={X1,X2,…,Xn}表示故障注入试验的序贯过程。

Xi=1表示故障注入试验后故障能被检测，Xi=0表示故障注入试验后故障不能被检测。此外，定义A和B分别为λ(X)的上下阈值，则判决准则可表示为：

1）如果λ(X)≥A，停止验证试验并接受假设H0，试验通过；

2）如果λ(X)≤B，停止验证试验并接受假设H1，试验失败；

3）如果B＜λ(X)＜A，继续验证试验。

判决阈值A和B由双方风险值α和β确定。其定义式为[18]：

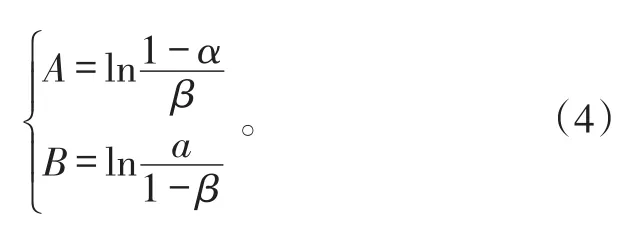
较之单次抽样方法、二次抽样方法等而言，SPRT方法所需平均样本量最小。但受验证试验结果随机性的影响，实际序贯试验过程中会出现样本量较大的情形，甚至无法做出接收/拒收的情况。针对该问题，一般采用截尾的方式对试验所需样本量进行限制。当序贯试验样本量达到截尾值nt时，对其进行强制性判决。由以上分析可知，截尾序贯判决过程在工程实施方面较为复杂，为解决这个问题，通常采用序贯试验图这一直观的图形化方式来进行判断分析，具体如图1所示。

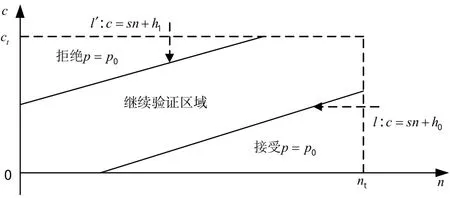
图1序贯概率比方法判决过程示意图Fig.1 Decision process schematic diagram of sequential probability ratio method

图1中，横轴表示当前注入故障样本量n，纵轴表示当前累计检测/隔离失败数c。直线l:c=sn+h0为试验次数为ns的接收边界，直线l′:c=sn+h1为试验次数为n的拒收边界。图1中，当试验次数未达到截尾次数时，图中区域被划分为拒收区、继续试验区和接收区。

其中，l和l′直线的斜率为s，直线l在c轴上的截距h0和直线l′在c轴上的截距h1的表达式为：

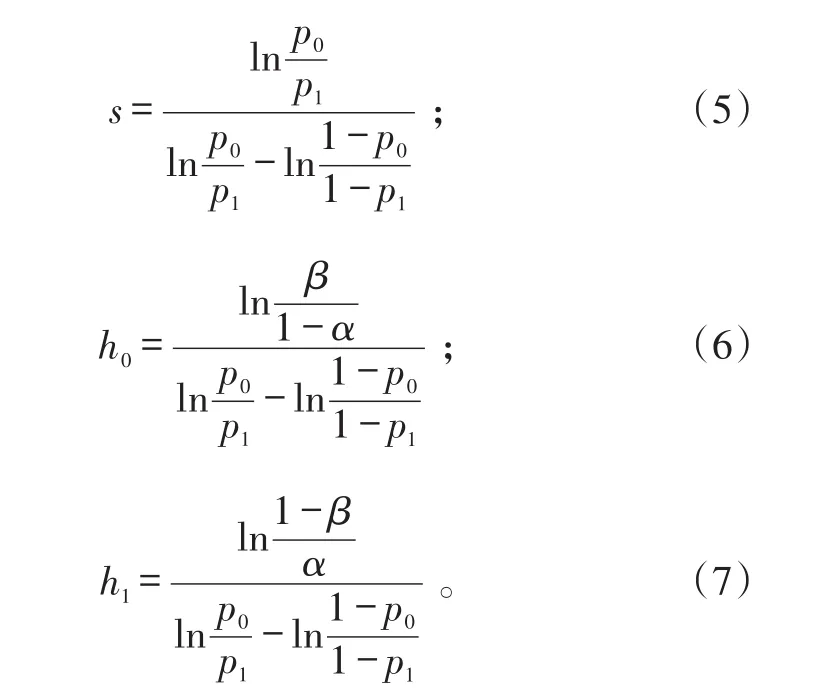
当试验次数未达到规定截尾数nt时，判决标准为：

1）若c≤sn+h0时，接收假设H0，判定为接收；

2）当c≥sn+h1时，接收假设H1，判定为拒收；

3）当sn+h0＜c＜sn+h1时，不做出判决，继续开展验证试验。

当试验次数达到规定的截尾数nt时，根据截尾判决准则做出判定。截尾准则为：

1）若n=nt且c＜ct，判定接收；

2）若n=nt且c≥ct，判定拒收。

2 基于故障率的样本分配方法

在测试性验证试验中，当样本量确定完成后，即可建立故障样本集，选取最具代表性的故障模式。该过程包含样本量分配和故障模式选取2个步骤。

根据相关标准[4，8]，在故障模式选取中，单次抽样方案与SPRT方法制定试验方案所需步骤方法存在较大差异。单次抽样方案采用的是先分配样本量，再抽取故障模式的方式，而SPRT方法采取序贯验证的方式导致其每次仅能注入一个故障，须要先确定故障模式选取单元，再基于该单元抽取故障模式。

2.1 故障模式单元选取

通过分析装备的FMECA信息，对用于故障模式抽样单元选取的数据进行整理。然后，实施对故障模式抽样单元的选取，具体步骤如下。

1）确定构成某型装备控制系统的主要单元，将系统划分到可进行故障样本量分配的装备层次，具体可划分为子系统、部件、模块等，假设在这些层次内共有n个单元。

2）通过FMECA分析，对每个进行样本量分配的单元，收集单元故障率λi、该单元的个数Qi和单元的工作时间系数Ti等相关数据。

3）根据上述获取的数据，计算该单元总的故障率QiλiTi，然后对每个单元的相对故障发生频率进行分配，即有：

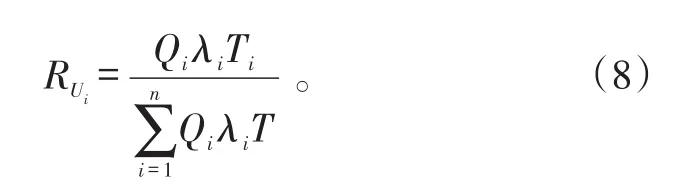
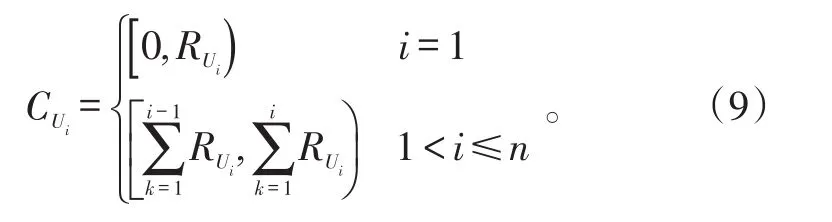
2.2 故障模式选取

装备故障模式信息主要用于故障模式的选取，构建用于测试性验证的故障样本集。假设模式选取的单元内共有故障模式数为m，且每个故障模式的故障率为λi（每个故障模式对应唯一的故障代码）。

基于此，可得到故障模式的选取实施步骤如下。

1）对每个故障模式的发生频率λiSi进行计算，则

可以得到每个故障模式的相对发生频率为：

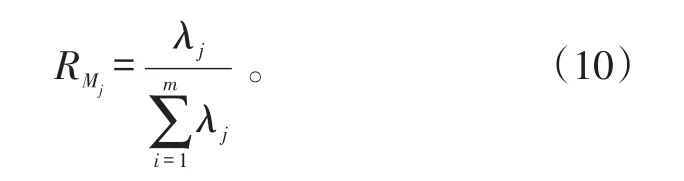
2）确定每个故障模式的相对发生频率的累积范围，可通过如下公式进行确定：

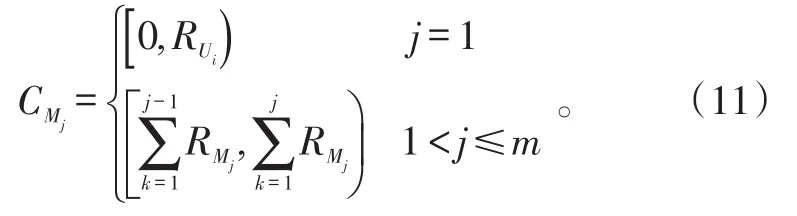
3）通过仿真生成0-1区间上均匀分布的随机数，然后与的累积范围进行比较，若随机数位于区间内，则选取该故障模式。

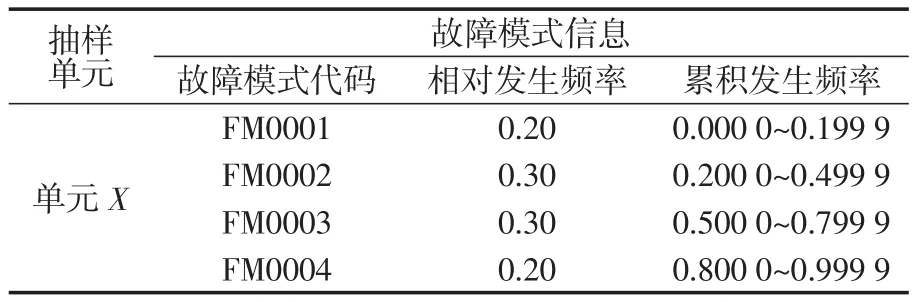
表1 故障模式抽样举例Tab.1 Example of failure mode

例如，在抽样时产生的随机数为0.60，从表1中可以看出，其落在故障模式FM0003的累积频率区间内，因此，选中故障模式FM0003，以上步骤均可以通过计算机仿真实现。

3 仿真分析

实验规定约束参数：生产方要求值：p0=0.95，使用方要求值：p1=0.90，生产方风险：α=0.1，使用方风险：β=0.1，以某型导弹飞行控制系统为研究对象，通过仿真数据对序贯设计过程进行判定。

由式（1）可得，经典抽样方案结果为（187，13），即须要注入的试验样本量为187，最大允许失败次数为13。在上述约束参数下，经典方法和SPRT方法的抽样特性见图2，SPRT方法的平均试验次数曲线见图3。

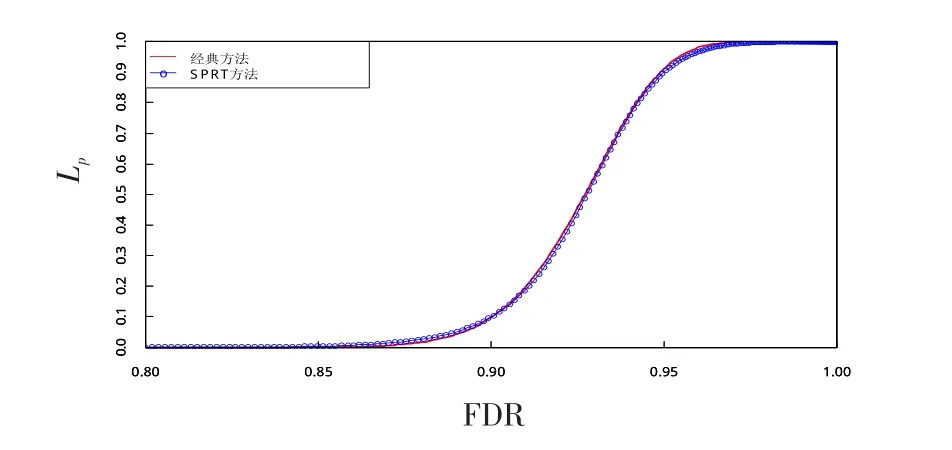
图2 不同方案抽样特性曲线对比Fig.2 Comparison of sampling characteristics of different schemes

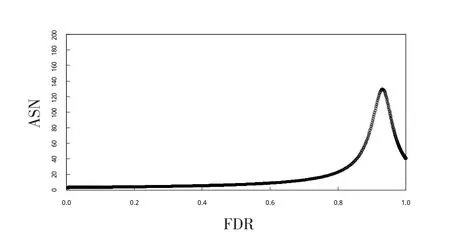
图3 SPRT方法平均抽样次数Fig.3 Average sample number of SPRT method

从图2中可以看出，经典验证方法和SPRT方法拥有几乎相同的抽样特性曲线，图3反映出SPRT方法的平均抽样次数要小于经典方法，其最大平均样本量为130。

图4为基于故障模式单元抽取和故障模式抽取，通过仿真数据实现测试性验证的序贯设计过程。图中的横坐标表示仿真试验次数，即故障注入的序贯过程，图中的纵坐标表示每次故障注入后的似然函数比，实际仿真过程中，第15次及第33次进行故障注入试验后，故障检测失败，即对应的Xi=0。因前14次故障注入试验中故障均能被检测，由式（3）可知似然概率比和序贯试验次数呈线性关系。第15次以及33次故障注入试验使得似然概率比降低，所以图中出现跳变，而第15—32次以及33—69次序贯试验故障均能被检测，所以也呈现线性关系。在第69次序贯试验之后，似然概率比的值超过了判据阈值A，所以停止试验，进行判定。

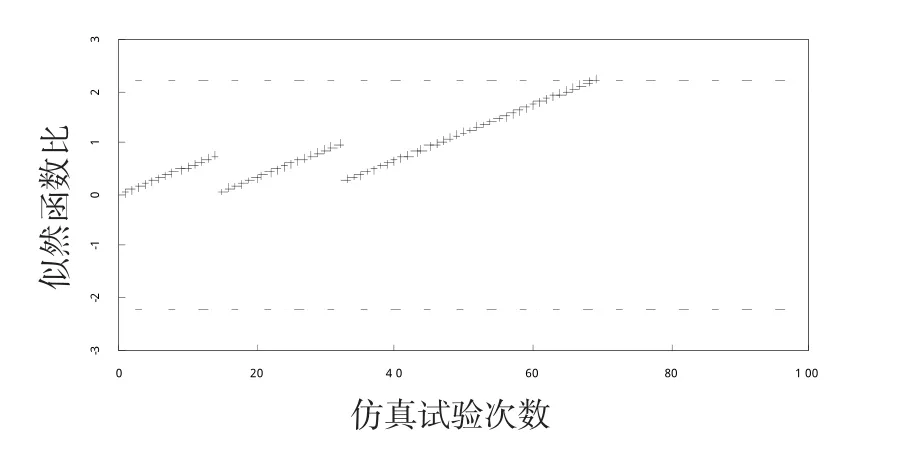
图4 测试性验证序贯设计仿真实现Fig.4 SPRT simulation

利用仿真试验数据，给出了验证试验的序贯过程和λ(X)的变化曲线。可以看出，λ(X)在2次失败检测处有下降。当试验次数为69时，λ(X)超过了接收判决阈值，判断接收，进一步说明SPRT方法对应的实际样本量为69，要优于经典验证方法所确定的故障样本量。

事实上，本文所提出的基于仿真数据的测试性序贯设计方案对于实际装备的应用有明显的指导作用。对实际装备进行测试性验证试验时，序贯设计过程同样包括判决阈值确定、装备故障模式单元选取、故障模式选取以及装备的接收/拒收判据等环节，相对于仿真试验而言，由于装备故障注入试验的限制，序贯试验过程需要更加严谨，充分利用装备研制阶段收集整理的数据也是需要进一步研究的，通过这种序贯的方式，达到减少验证试验所需故障样本量以及缩短试验周期的目的。

3 结论

本文将二项分布模型下的SPRT方法应用于某型装备控制系统的测试性验证，介绍了在序贯试验方案下基于故障率的故障样本量分配和故障模式选取方法。经过仿真验证，在相同的试验约束参数下，所需样本量SPRT方法要小于经典方法。因此，SPRT方法可以作为一种有效的测试性验证试验方案制定方法。