一种快速高精度激光终端跟踪角度等效方法*

崔慧敏，郭宇龙，马纪军，关贵注，王宇宁

（北京遥测技术研究所 北京 100076）

引 言

作为一种以激光光束为载体直接进行信息传输的新的通信方式，空间激光通信凭借其传输速率高、通信容量大、保密性和抗干扰能力强等优点，在国内和国际上都得到了普遍重视[1,2]，在军用和民用领域也得到广泛应用[3,4]。但是激光的发射光束窄、发散角小[5]，且通信距离远，易受复杂大气环境影响。因此，对激光通信终端进行高精度视轴指向控制，对建立和保持高质量且稳定的激光通信链路具有关键性作用。为保证激光通信终端始终跟瞄对方以保证通信链路的畅通，目前激光终端多采用粗精组合控制的方式实现视轴的高精度指向[6,7]。其中粗环的主要作用是实现目标的扫描捕获和视轴初始指向[8]。受机械谐振，传感器噪声以及内外部干扰因素的影响，粗跟踪环对脱靶量的补偿精度有限[9]。为进一步补偿粗跟踪的残差，通常系统中包含由快速反射镜构成的精跟踪环路，实现对目标激光终端信标光的高精度指向。

相比于转动惯量较大的粗跟踪环U型架负载，快速反射镜惯量较小，带宽较高，可以对输入进行快速有效的响应[10]。为了制定良好的粗精环控制切换策略，需要提高目标指向精度，最大化粗精环指向角度等效转换精度。而目前针对解决该问题的相关文献较少，且坐标转换方法通常使用四元数法[11]，通过某一点在已知坐标系下的坐标不断乘以坐标旋转矩阵得到该点在目标坐标系下的坐标。当经过多次旋转坐标转换后，会导致最终的方程较为复杂，目标在已转换坐标系下的位置较难求解。

为解决该问题，本文提出一种新的解决思路，以U型架为基准实现从中间向两端进行坐标转换。该方法相对于端到端的坐标转换，计算简单且精度较高。文中首先建立了激光终端各坐标系，并建立了坐标系之间的转换关系矩阵，接着介绍了使用传统的端到端坐标转换方法，进行粗跟踪环和精跟踪环等效角度转换过程，然后提出了一种新的解决思路，并对两种方法的转换结果精度和计算复杂度进行对比分析，最后给出了结论分析。

1 激光终端坐标系建立

为了方便进行角度等效转换，首先需要建立坐标系。跟踪快速反射镜坐标系和粗跟踪环U型架坐标系的示意图如图1所示，其中M1反射镜，库德镜1，库德镜2，库德镜3和第3反射镜均处于U型架坐标系中。快速反射镜可以绕着x轴，y轴做旋转运动。以粗跟踪环U型架为基准建立空间坐标系x1y1z1，U型架可以绕着z1轴做方位运动，也可以绕着轴y1做俯仰运动。激光光束通过跟踪快反镜，M1反射镜，3个库德镜和第三反射镜反射后最终指向激光信标的位置。

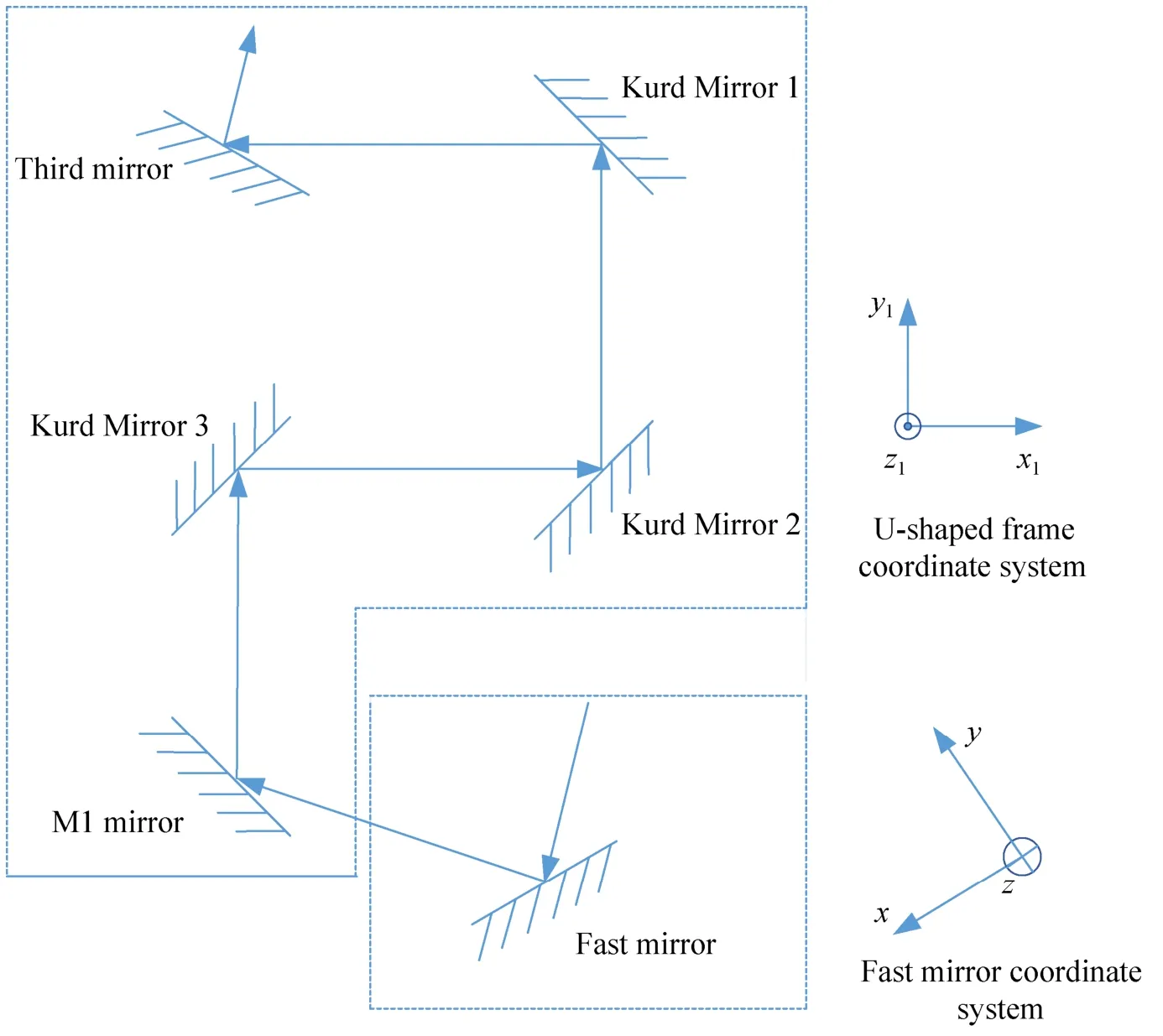
图1 U型架和跟踪快速反射镜坐标系Fig.1 The U-frame and tracking fast mirror coordinate systems

2 端到端的粗精环角度等效转换方法

2.1 快反运动引起光线变化过程

假设在快速反射镜坐标系下有一束光入射到跟踪快反镜上，则快反运动引起的光线变化过程如下：

Step1：将跟踪快反坐标系先绕x轴逆时针转动α1（所对应的转换矩阵为R1，表示方法以下类同），再绕z轴逆时针转动β1（R2），到达新的跟踪快反位置。

Step2：快反坐标系，绕z轴顺时针转β1（R3），再绕x轴顺时针转α1（R4），接着绕z轴逆时针转动135°（R5），再绕x轴顺时针转45°（R6），可得到M1反射镜坐标系。

Step3：M1反射镜坐标系，先绕x轴逆时针转动90°（R7），再绕本体坐标系z轴逆时针转动α3（R8_1），可得到库德镜3坐标系。

Step4：库德镜3坐标系，绕x轴顺时针转动180°（R9），可得到库德镜2坐标系。

Step5：库德镜2坐标系，绕x轴顺时针转动90°（R10），可得到库德镜1坐标系。

Step6：库德镜1坐标系，绕x轴逆时针转动45°（R11），再绕z轴逆时针转动135°（R12），再绕本体坐标系y轴顺时针转动β3（R13_1），得到终端本体坐标系。

假设一束光线在初始跟踪快反坐标系下的坐标为[x0y0z0]，将快反坐标系的输入光线，经过多次坐标变化和反射，可得到最终输出光线在终端本体坐标系下坐标为[x1y1z1]：

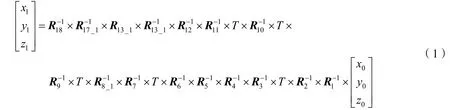
其中R17_1为绕本体坐标系z轴顺时针转动α3，R18代表绕z轴逆时针转动45°。

2.2 转台转动引起的光线变化过程

假设跟踪快反镜转动角度α1=0，β1=0。U型架在初始位置基础上绕z1轴逆时针转动到新的角度α2，绕y1轴顺时针转动到新的角度β2。即按以下步骤进行旋转变换：

Step1：在跟踪快反镜初始位置下，先绕z轴顺时针转β1（R3），再绕x轴顺时针转α1（R4），接着绕z轴逆时针转动135°（R5），再绕x轴顺时针转45°（R6），到达M1反射镜。

Step2：在当前坐标系下，先绕x轴逆时针转动90°（R7），再绕主z轴逆时针转动α2（R8_2），到达库德镜3。

Step3：在当前坐标系下，绕x轴顺时针转动180°（R9），到达库德镜2。

Step4：在当前坐标系下，绕x轴顺时针转动90°（R10），到达库德镜1。

Step5：在当前坐标系下，绕x轴逆时针转动45°（R11），再绕z轴逆时针转动135°（R12），再绕主y轴顺时针转动β2（R13_2），到达第三反射镜。入射光线经过多次反射，最终输出光线在U型架坐标系下坐标为[x2y2z2]：

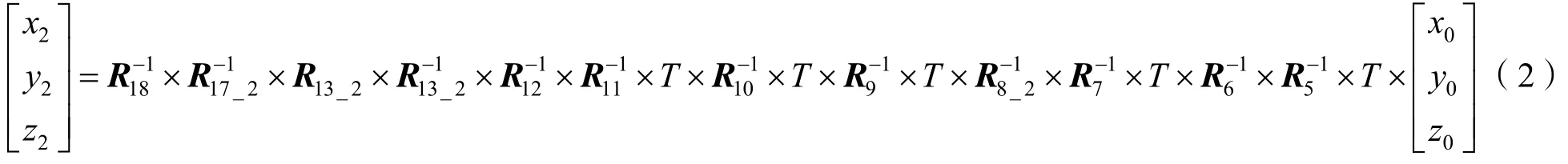
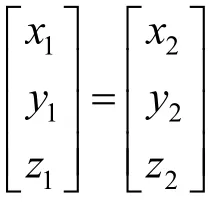
3 基于从两端到中间参考坐标系的角度等效转换

假设快速反射镜在x，y方向的偏转角度分别为Δx，Δy。在快速反射镜坐标系下，入射光线坐标为[-1 0 0]。跟踪快速反射镜初始法线为。跟踪快反运动后的法线和M1反射镜法线分别为

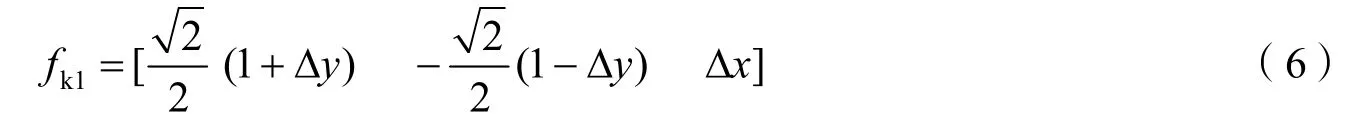
则入射光线经过快速反射镜和M1反射镜反射后，在XOY平面上产生的变化为

U型架上库德镜3、库德镜2、库德镜1和第三反射镜初始法线分别为

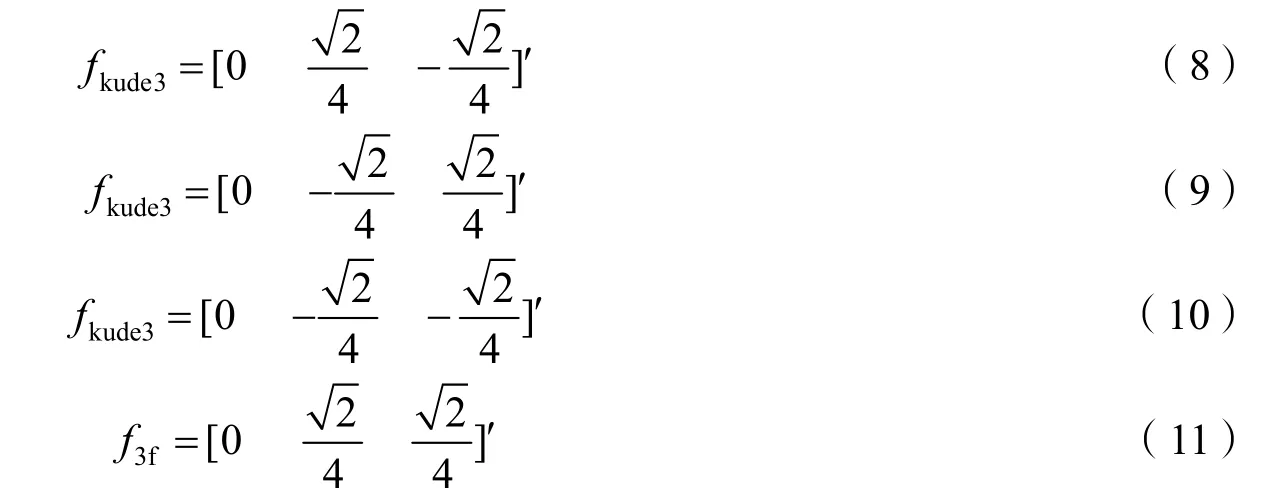
第三反射镜绕y轴转动β角，旋转矩阵为Ry，四个反射镜均绕z轴旋转α角，旋转矩阵分别为Rz。旋转后库德镜3、库德镜2、库德镜1和第三反射镜的新的法线方向如下：

当有一束入射光线[0 0 1]，经过多个库德镜和反射镜反射后，最终输出矢量为

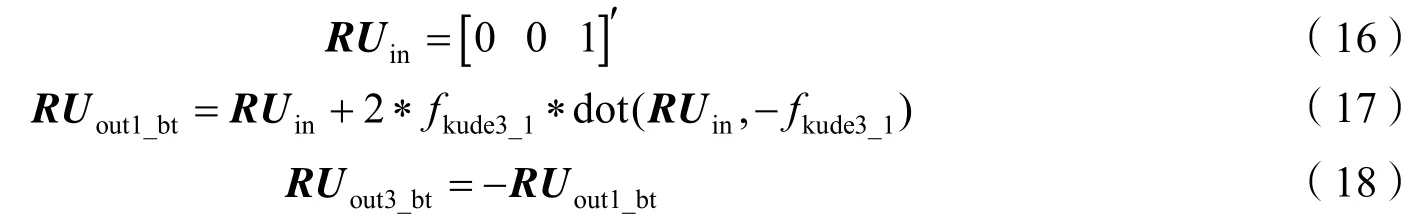
当输入矢量为[ΔxΔy1]时，输出矢量分别为

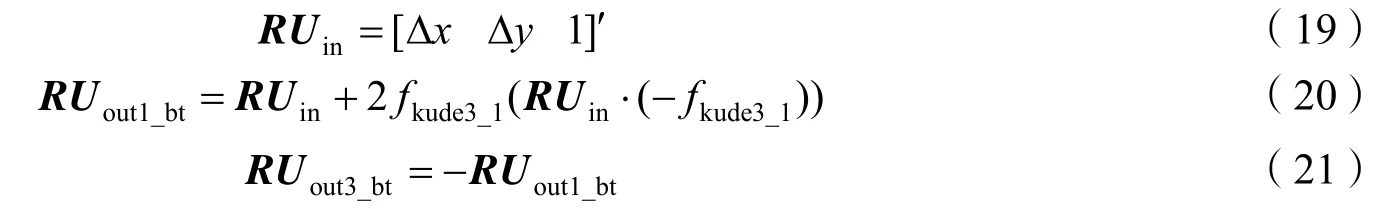
将矢量变换到U型架坐标系

假设RUout3=［x3y3z3］′，第三反射镜矢量在U型架坐标系为

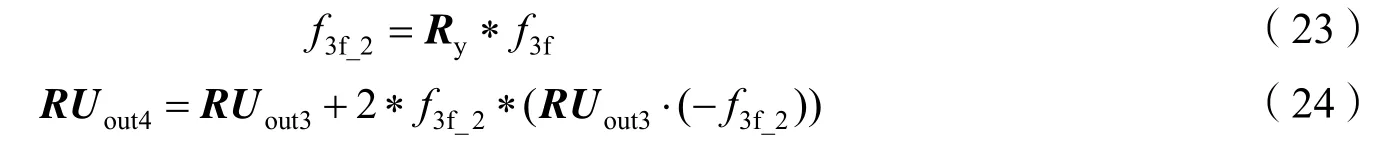
从整个推导过程可以很容易看出，方法二要比方法一计算量小，使用MATLAB对两种方法的转换结果进行计算，由于方程的解很长，这里不再一一列出，但方法二的解很明显要比方法一的解简单很多，且很多情况下，在相同的输入条件下方法二可以很容易得到等效解，但方法一在该条件下却无解。第一种从端到端的坐标转换方法其本质是通过坐标系的旋转得到转台新角度，快反镜角度和转台原来角度之间的关系(α2,β2)=f(α1,β1,α3,β3)，从而进一步得到转台角度变化量和快反镜方位、俯仰角度之间的直接转换关系

从公式1和公式2可以看出，转换过程需要多个矩阵的乘法运算，这对于对实时性要求较高的底层控制器来说，计算量太大。另外，由于激光波束宽度有限，对快反镜的调节角度范围通常在10个微弧度量级，过多的转换过程会导致最终的计算误差增大，严重情况下有可能造成目标跟踪丢失。而本文提出的第二种从两端到中间的坐标转换方法，取U型架坐标系为中间参考坐标系，将不同条件下光线坐标变化同时映射到U型架坐标系中进行对比分析，并采用法线旋转，点积运算等手段，使得计算过程在每一阶段都有精确的结果输出，有效地减小了计算量，满足工程应用中对实时性的要求。

如在U型架方位角和俯仰角分别为30°、60°情况下，如果快反镜在x方向和y方向的转动量分别为0.01°和0.02°，入射光线坐标为（-1，0，0），经过快反镜和M1镜反射后，光线在xoy平面产生的变化量为[0.0399，-0.0144，0.9991]，经过库德镜3反射后，该矢量在U型架坐标系的坐标为[-0.0187，-1，-0.0123]，经过库德镜2、库德镜1和第3反射镜反射后，该矢量坐标为[0.0013，0.0223，1]。令快反镜在x和y方向没有转动量，将该矢量转换到U型架坐标系，从而得到方位轴和俯仰轴角度变化量为-0.0011547°和0.002°。而方法一由于转换矩阵和逆矩阵较多，MATLAB中最终得到的计算公式很长且无法化简，这对于处理能力有限的底层嵌入式控制器来说，无法实现工程应用。

4 结束语

为实现激光终端高质量稳定通信，对激光终端进行粗精控制切换时，为解决一系列复杂的坐标转换问题建立了合适的坐标系并采用两种方法对角度转换进行求解，并针对该激光终端研究对象，得出采用从两端向中间参考坐标系进行转换的方法比从端到端的坐标转换方法的计算量小，且求解精度高的结论。这为激光通信终端的精确、平滑指向提供了理论基础，对促进我国空间激光通信事业的发展具有重要的意义。