概率统计关于“善学”的引导与创新实践

张德然，赵克全，石蓉荣

（1.亳州学院 电子与信息工程学院；2.亳州学院 教务处，安徽 亳州236800）

习近平总书记在北京八一学校与师生座谈时指出：“广大教师要做学生锤炼品格的引路人，做学生学习知识的领路人，做学生创新思想的领路人，做学生奉献祖国的引路人。”［1］使命呼唤担当，责任引领未来，学生以学为主，作为一名专业课教师，除了要与政治思想课同行，挖掘教材中德育因素树德育人外，还要为学生的学习知识引好路，要在不间断的知识传授中培养学生“愿学”、“善学”，强化创新意识和创新思想并勇于创新，为促成合格的社会急需的“复合型”人才做出努力。

概率统计是研究随机现象统计规律的科学，概率统计的思维结构是一个多因素的动态关联系统，由脑内神经元兴奋模式的各种运动对概率统计对象的信息进行加工和处理，从而形成不同类型的概率统计思维模式［2］。多年的教育实践表明，依据概率论及数理统计自身的特点，利用其与其他学科的广泛联系，可以较大程度的挖掘学生的潜能，提升学生的学习积极性。但要显著大面积提高学习效果，必须构建一个“善教”、“善学”的和谐链。

一、注重学科知识的融通，催生“善学”

“愿学”是“善学”的前提，启发式的说教虽有效果，但学科教育的效果更能激励学生的学习热度，并能保持渐进持续度。这种自然而然的效果来自教师对学科资源的开发，并在培养学生创新意识和行为中起着潜移默化的作用。如在古典型概率的计算中，常常用排列组合来计算两种基本事件总数，基于此，同样可以利用概率的方法去解决排列组合问题。

例 1［3］证明，

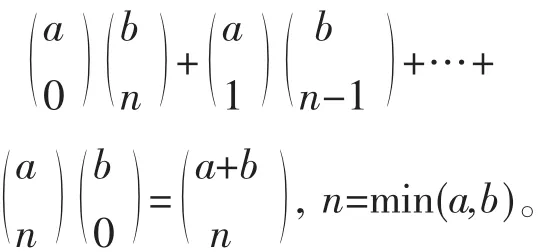
证 设计如下概率模型：一批产品共有a+b个，其中a个不合格品，b个合格品，从中随机取出n个，n=min(a,b)。则Ak={取出的n个产品中有k个不合格}，其概率：

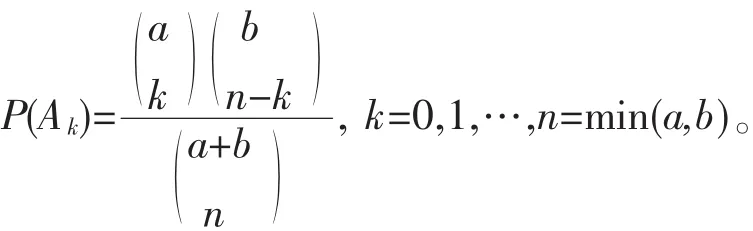
由诸 Ak互不相容，且 P（A0∪A1∪A2∪…∪An）=P(Ω)=1得：

即有：

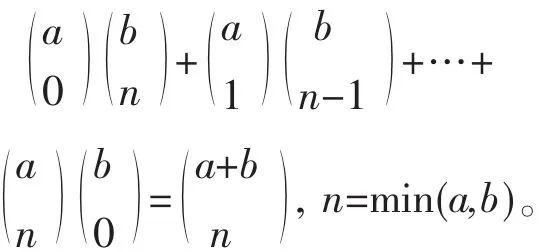
数理统计中也有许多类似的情况。

例 2［4］证明是半正定的。

证

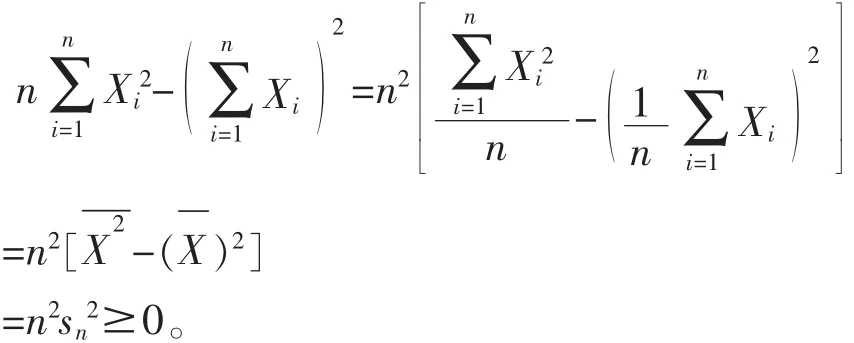
概率论与统计的方法不仅在自然科学领域中有着广泛的应用，在社会科学领域中同样也有着广泛的应用。例如“小概率原理”在一些文学创作中比比皆是。在电视剧《重庆谍战》中有这么一个情节：日军绑架了爱国将领卢躬庶，逼他说出打进日军内部的“内鬼”，日军对其实施了各种酷刑，他宁死不开口；当其奄奄一息之时，狡猾的日军军官佐佐木对卢说，你不说我们也知道，“内鬼”就是秦敖！此时卢并不否定，而是坦然地说：“内鬼”就是秦敖，真叫你猜中了！日军认为，酷刑都征服不了他，他临死前轻易供出内线是不可能的，于是错误地认为他临死前想挑起内讧，借刀杀人。就这样，卢老将军利用“小概率原理”巧妙地保护了自己的同志,作者利用“小概率原理”使得剧情的发展更可信。黄秦安先生指出：“数学作为联结自然科学与人文、社会科学的纽带，扮演着沟通文理、兼容并蓄、弥合文化裂痕的文化使者的角色。”［5］马克思也明确指出：“一门科学只有当它达到了能够成功地运用数学时，才算真正发展了。”［6］文学源于生活，必然传递着希望，偶然呈现着曲折，一旦把它根植于文理融合思维的肥沃土壤中，它的成长就将会更加茁壮！

有位学生在学习概率论课后深有感触地写道：通过概率论课程的学习，使我进一步感受到了概率论的强大魅力，不仅是其在数学解题中的应用，其在文学、历史等领域的广泛应用更是令我耳目一新。笔者认为这应该也是为什么要求教师学识渊博的原因吧！视野开阔，涉猎广泛，才能形成灵活的方法，活跃的思维，也才能教得好学生。学生们的话语，既道出了对这种方式的向往，又说出了对老师如此而为的期待，善教、善学，构建了课堂一道靓丽的风景线。

二、注重知识的发生过程，激励“善学”

学习任何一门知识都要知其然，又要知其所以然。现代教育理念要求教师不单单授人以“鱼”，还要授人以“渔”就是这个理。要做到这一点，教师就必须认真钻研教材，理清知识的来龙去脉及如何向同学传授，“知之深切，方能行之自觉”。比如，在学习概率的间接计算方法时，利用概率的公理化定义，首先应由概率的可列可加性推出有限可加性，然后由此并同时利用非负性及规范性就可依次得到事件差、逆及一般事件和的概率公式。依据明确：化一般为互斥；推理顺畅：和的概率等于概率的和。在假设检验中，结合陶行知先生的名言：行动生困难；困难生疑问；疑问生假设；假设生试验；试验生断语；断语又生了行动，如此演进于无穷。通过分析假设检验的程序，就可以让学生明白假设检验的合理性及该如何进行。合理的思考，严谨的推理，纳入同学的认知结构，就一定会化为解决问题的正能量，形成“善学”的催化剂。

三、注重知识的延伸推广，提升“善学”

兴趣是一种向往，是推动学习的内部动力，是塑就创新理念的前提。概率论与数理统计的问题大都来自社会，来自生活，甚至就在我们的身边。所以，对概率论的学习来说，如此的贴近生活、贴近社会，加之教师的引导已足以让学生感兴趣了。但如何利用这种兴趣集聚正能量，唤起学生的创新意识，培养学生的创新精神，提高学生的创新能力，是要进行认真设计的。教学的经历告诉我们，注重知识的延伸推广是一条有效途径。如“抓阄问题”是古典概率中一个常见例子，稍加改造可转变为下述“摸球问题”。

例3 袋中有a只黑球，b只白球，它们除颜色不同外，其它方面没有区别，现把球随机地一个个摸出来，求第k次摸出的一只球是黑球的概率（1≤k≤a+b）。

调查显示，从事竹林经营的家庭劳动力以1～2人为主，平均为1.64人，且随其家庭经营竹林规模的增加而稍有增加，经营面积接近1.33 hm2时劳动力人数达到最大；户均从事竹生产天数也表现出与此一致的规律。可见，由于竹林经营面积小吸纳不了太多的劳动力，致使剩余劳动力只能从事其他非竹行业。

发现1：此题有5种解法，但最优解法为：只考虑第k次抽球，a+b个球中任何一个都有可能在第k次被抽到，故样本点数为a+b，抽到黑球只有a种可能。令A：“第k次摸出的一个球是黑球”，则有：

因为它构建了最小的样本空间，使得计算更加方便。

发现2：第k次摸到黑球的概率与k无关。即结果与次数无关，所以“抓阄”不需争先恐后。

发现3：利用例中结果及等价事件转化法可以解决下述诸多问题：某人有n把钥匙，其中只有一把能打开他的门，他逐把取出钥匙试开，求到第i次打开锁的概率；袋中有a只黑球，b只白球，甲、乙、丙3人依次从袋中取出1球（取后不放回），试分别求3人各自取得黑球的概率；袋中有a只黑球，b只白球，把球随机地一只只取出来（不放回），直至袋中剩下的球全为一色球为止，求最后剩下的全是黑球的概率。

发现4：此例的结果与其他方法相结合，可简化复合事件的概率计算：甲、乙2只袋，分别装4份、8份报名表，其中女生的报名表分别为2份、6份，现任取一袋，并从中先后取出2份报名表。

（1）求先取出那份是女生报名表的概率；

（2）已知后取出的是男生的表，求先取出那份是女生表的概率［7］。

如此等等，从题内到题外，从课内到课外，不间断的联想就会孵化出创新的意识与行动，并在日后许多问题的解决中发挥作用。

四、注重研讨推进，强化“善学”

心理学的研究表明,意识是产生渴望的前提，没有渴望就没有追求，只有具有强烈的参与意识才能经常付诸行动［8］。信任拉近距离，尊重构建和谐，和谐的师生关系会有力地拉动师生的积极参与。实践证明，在概率论与统计学的教学中经常性地开展以问题为背景的师生共同研讨不仅可以拉近师生之间的距离，而且可以引起学生的强烈追求和主动进攻，在不断的获知成功中走向更大的成功。

例4 甲、乙2射手轮流对同一目标进行射击，其命中目标的概率分别为α和β，甲先射，谁先命中谁得胜，问甲、乙2人获胜的概率各是多少？

同学们通过一番研讨，大都给出了利用列举法所得的正确结果。这时，教师可引导学生回忆被积函数为三角函数与指数函数乘积时的分部积分方法，在教师的提醒下学生们通过一番“用心”终于发现了如文献［9］的解法。

冲破传统的繁琐，收获特色的简练，这就是“善学”的成果，而且它有很强的辐射力。事实正是这样，在以后的类似问题中，大家都这样做了。

例5 一迷宫设有3条路径，一人若沿第1条路径走3小时后即可走出迷宫，若沿第2条路径走5小时后又回到原处，沿第3条路径走7小时后也返回原处，假定此人随机在3条路径中选择1条，试求他平均要用多少时间才能走出迷宫。

解 设该人需要X小时走出迷宫，Y表示第一次所选的路径，{Y=i}即为选择第i条路径，由题设，得：

解得E(X)=15，即该人平均要15小时才能走出迷宫。

五、注重实践体验，推动“善学”

需要永远带有动力性［10］。适当的体验和实践会让学生在需要的成功中产生新的需求，新的需求会更加不间断地激发“善学”。因此，要紧密结合概率论和数理统计专业知识的学习，联系社会和学生实际，适时地让学生去做力所能及的体验和实践，从成功中集聚能量，在期望中推动“善学”。如在讲授正态分布后，要求学生用概率的方法计算广义积分：

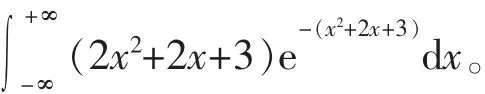
依据密度函数的性质及各阶矩等别开生面且简洁的解法不仅让学生们又一次体验到概率统计的美，而且还联想出一组可以用概率论方法求解的积分题。同样，根据数理统计学习的进展，可适时布置作业，让学生们通过阅读毕业论文估计文章的错别字个数;到教育实习基地采集数据评价实习效果等等。通过实践他们会加深对概率统计的感悟。这样的体检与实践自然会推动学生的愿学、“善学”。

凡此种种，不一而足。“善学”依赖“善教”，“善教”推动“善学”，概率论与数理统计的教学也不例外，作为教师要用思想升华思想，智慧启迪智慧，真正成为名副其实的服务于学生成长和促进学生发展的引路人。