建筑结构剪重比分析探讨及对规范限值的建议

金灿国，蔡凤维

（广东省建筑设计研究院 广州510010）

0 引言

在结构设计过程中，经常会碰到计算剪重比不满足《建筑抗震设计规范：GB 50011-2010（2016年版）》[1]（后文均称《抗规》）的最低限值要求，此时设计人员往往不知如何处理，本文将结合《抗规》条文，解析设计剪重比和计算剪重比主要影响因素，结合工程实例，也给出计算剪重比在不满足规范最低限值要求的情况下具体的处理意见和方法，了解哪些情况下计算剪重比难于满足设计剪重比要求；针对《抗规》设计剪重比限值提出一些建议。

随着建筑设计市场日趋成熟，甲方对设计单位的要求也越来越严苛，要求设计单位设计出快好省的图纸，优化结构设计就变成我们必须面对的一件非常头疼的事情，甲方会提出一堆设计优化参数指标，如何从这些计算参数指标中找到最为关键最为核心的参数指标尤为重要。作者依据多年的工作经验总结，从中找到了结构优化较为核心的计算参数指标-剪重比，本文将通过分析来探讨剪重比对于结构优化设计的重要性。

1 设计剪重比和计算剪重比解析

《抗规》5.1.4 条规定，建筑结构的地震影响系数应根据烈度、场地类别、设计地震分组和结构自振周期以及阻尼比确定。其水平地震影响系数最大值应按表1采用。特征周期应根据场地类别和设计地震分组按表2采用，计算罕遇地震作用时，特征周期应增加0.05 s。

表1 水平地震影响系数最大值Tab.1 Maximum Horizontal Earthquake Impact Coefficient

表2 特征周期值Tab.2 Characteristic Periodic Values（s）

《抗规》5.2.5 条规定，抗震验算时，结构任一楼层最小地震剪力系数值应符合表3 要求。

通过表1 和表3 中数值对比，可以看出规范要求的最小剪力系数值（设计剪重比）：λ=0.2αmax（扭转效应明显或基本周期小于3.5 s 的结构）；αmax仅与抗震设防烈度有关，故λ仅与抗震设防烈度有关。

表3 楼层最小地震剪力系数值Tab.3 Minimum Seismic Shear Coefficient of the Third Floor

参考廖耘等人[3]的研究成果，计算剪重比λ的本质关系可表述为：“各振型地震影响系数αj的平方”与“各振型参与质量系数θj的平方”的乘积之和的二次方根：

式⑴推导的前提条件是高层建筑各层均满足刚性楼板假定且不进行扭转藕联计算，此时计算剪重比主要由两个参数控制，各振型地震影响系数αj和各振型参与质量系数θj；其中αj与抗震设防烈度、基本周期、特征周期和阻尼比有关；θj与振型、结构重量有关。

2 计算剪重比深度剖析

《抗规》5.1.5 条规定，建筑结构地震影响系数曲线（见图1）的阻尼调整和形状参数应符合下列要求：

除有专门规定外，建筑结构的阻尼比应取0.05，地震影响系数曲线的阻尼调整系数应按1.0 采用，形状参数应符合下列规定：

⑴直线上升段，周期小于0.1 s 的区段。

⑵水平段，自0.1 s 至特征周期区段，应取最大值αmax。

⑶曲线下降段，自特征周期～5 倍特征周期区段，衰减指数应取0.9。

⑷直线下降段，自5 倍特征周期～6 s 区段，下降斜率调整系数应取0.02。

图1地震影响系数曲线Fig.1 Seismic Influence Coefficient Curve

从图1 可以看出，Tg～5Tg之间地震影响系数趋近于双曲线下降段；5Tg～6 s 之间，下降斜率调整系数取0.02，地震影响系数趋近于水平，此时长周期下计算所得的水平地震作用下的结构效应可能太小，出于结构安全的考虑，《抗规》和《高规》均提出了对结构总水平地震剪力及各楼层水平地震剪力最小值的要求（相当于地震作用下，给出地震剪力最小限值要求），规定了不同烈度下的剪力系数，当计算剪重比不满足但接近设计剪重比时，可调整结构总剪力和各楼层的水平地震剪力使之满足要求；当计算剪重比小于设计剪重比较多时，需改变结构布置或调整方案；结合特征周期取值表2 分析可以得出结果如表4 所示。

表4 地震影响系数与基本周期关系Tab.4 Relation between Earthquake Impact Coefficient and Base Cycle

从表4中分析可以得出，场地类别越好，设计地震分组越小，特征周期越小，结构基本周期落入5Tg～6 s之间概率越大，即位于反应谱的位移控制段（即地震影响系数趋于水平段）概率越大；结合式⑴可知，结构基本周期落入5Tg～6 s，调整结构刚度对地震影响系数影响很小，继而对计算剪重比影响也很小，此时需要通过调整结构布置或结构体系使得计算剪重比接近设计剪重比，代价巨大。

规范剪重比限值与场地特征周期无关，结合表4分析可知，特征周期越小，越难满足规范设计剪重比，反之特征周期越大，更容易满足设计剪重比，因此可能造成特征周期越小，场地条件越好，剪重比控制过于严格，特征周期越大，场地条件越差，剪重比控制过松。建议文献[1]规范编制组，考虑设计剪重比与特征周期挂钩，特征周期越小，设计剪重比限值取小，特征周期越大，设计剪重比限值取大。

为了验证式⑴推导的正确性及上述结论的合理性，我们通过实例来进行分析验算；实例1 为一高层住宅建筑，剪力墙结构，抗震设防烈度7 度，地震基本加速度0.1 g，场地类别Ⅰ0类，地下3 层，地上32 层，通过刚度调整前后两个模型的计算结果进行对比分析。

根据《抗规》3.4.3 条规定，结合计算结果判断结构平面和竖向均规则，表5 列出结构刚度提高前后前三阶振型基本情况，通过表5 可知，结构刚度提高前后第1、第2 基本周期平动系数均超0.9 以上，周期比均小于0.6，前后两个模型都是体型规整的结构，可不进行扭转藕联计算，且各层均满足刚性楼板假定，满足式⑴手算剪重比的前提条件；表6 列出了此高层住宅建筑在计算初始条件不变的情况下，增加刚度前后整体计算指标对比（包括计算剪重比）；表7 通过式⑴手算增加刚度前后计算剪重比；增加刚度前电算计算剪重比为1.246，手算剪计算剪重比为1.23，增加刚度后电算计算剪重比1.322，手算计算剪重比1.27，均在5%的误差范围内；表7 中基本周期及振型参与质量系数均来自电算结果，故初步分析电算与手算误差主要由于地震影响系数计算精度造成，初步验证了式⑴推导的正确性。

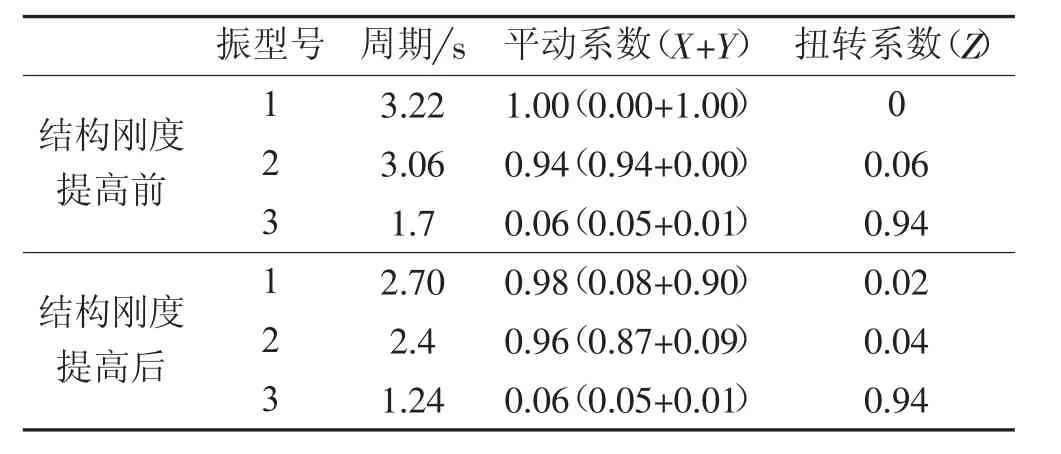
表5 前三阶振型基本情况（结构刚度提高前后）Tab.5 Basic Conditions of First and Third Modes（before and after Structural Stiffness Increases）

从表5可以看出，结构刚度提高前后，结构前三阶振型基本周期均位于反应谱的位移控制段（见表4），位移角由1/1 036 减小至1/1 880，结构前3 阶振型基本周期减小了将近0.6 s，说明刚度有了显著的提高，但底部总剪力仅增加9.7%，计算剪重比仅提高6.1%；结合式⑴分析，前三阶基本周期均位于反应谱的位移控制段，故前三阶振型地震影响系数αj调整前后变化很小，且前三阶振型质量参与系数均接近60%，是导致在刚度有了显著的提高情况下，底部总剪力和计算剪重比变化不大的主要原因。

表6 计算整体指标对比（结构刚度提高前后）Tab.6 Comparisons of Overall Indicators（before and after Structural Stiffness Increases）

表7 手算剪重比对比（结构刚度提高前后）Tab.7 Hand-calculated Shear-weight Ratio（before and after Structural Stiffness Increase）

综上分析，体型规则的建筑结构，通常前3 阶振型振型参与质量系数占比超60%以上，如果前三阶振型结构基本周期落位于反应谱的位移控制段（即地震影响系数趋于水平段），此时通过提高结构刚度来加大地震影响系数，从而提高计算剪重比，以便满足规范设计剪重比限值的要求，可能需要付出非常大的代价；故建议计算剪重比不满足规范设计剪重比限值要求的情况下，若前三阶振型结构基本周期大小在Tg～5Tg之间，或稍大于5Tg，此时可以通过提高结构刚度，来加大地震影响系数，从而提高计算剪重比，满足规范设计剪重比限值要求；若前三阶振型结构基本周期远大于5Tg，此时要满足规范设计剪重比，可能需要调整结构体系和总体布置，以便计算剪重比接近设计剪重比。

一些体型不规则的建筑结构，前3 阶振型振型参与质量系数占比小于60%，高阶振型振型参与质量系数占比增加，从而使计算剪重比更大，更容易满足设计剪重比的要求，这与建筑设计应优先选用规则的形体的设计原则相违背；故建议文献[1]及文献[2]规范编制组，其他设计参数指标均满足规范要求的前提下，是否可以考虑剪重比不满足0.2αmax时，均可通过乘以增大系数方法来处理；或者修改反应谱曲线来使结构满足设计剪重比的要求。

3 结构设计优化核心指标-剪重比

结构设计优化往往可分为两大方面，计算和配筋；其中计算是设计优化的主要因素，计算又包括前处理和后处理，前处理包括结构选型优化、荷载优化、地震参数输入正确、抗震等级输入正确、风荷载参数输入正确等，后处理主要包括刚度比、承载力比、质量比、刚重比、周期比、剪重比、位移角、位移比、轴压比、配筋合理性等等参数指标；如何能够设计出经济、合理、安全的设计作品，就需要我们能够抓住其中关键性的技术指标。

结构选型优化、荷载优化、地震参数输入正确、抗震等级输入正确、风荷载参数输入正确等这些前处理参数设置比较好把握，也不会有太多的争议；计算结果是否经济、合理、安全，主要看后处理参数指标，刚度比、承载力比、质量比、刚重比、轴压比也比较好把握，关键在于如何通过周期比、剪重比、位移角、位移比这些参数来判断结构刚度是否合理，从而判断设计的经济性和合理性。一些优化设计人员通常把位移角满足并接近规范最低限值要求作为刚度合理性的重要指标，其实这种观点存在比较大的缺陷。

当结构布置不合理，抗扭刚度比较弱的情况下，第1、第2 平动周期扭振成分较大，算出来的位移角即便接近规范限值，但也并不能说明结构刚度就是合理的，此时剪重比可能远远大于规范最低限值要求，实际结构刚度很大，只能说明结构布置不合理，需要尽量的调整结构布置。

什么情况下可以判断结构布置、结构刚度是合理的，可以通过图2 的形式来表达。

图2 结构计算优化设计流程图Fig.2 Flow Chart of Structural Optimization Design

从以上分析可以得出，剪重比是判断结构布置、结构刚度合理性的核心指标。

4 结论和建议

⑴规范设计剪重比仅与抗震设防烈度有关，计算剪重比主要由两个参数控制，各振型地震影响系数αj和各振型参与质量系数θj；其中αj与抗震设防烈度、基本周期、特征周期及阻尼比有关；θj与振型、结构重量有关。

⑵基本周期大小落在Tg～5Tg之间，或稍大于5Tg，此时可以通过提高结构刚度来加大地震影响系数，从而提高计算剪重比，满足规范剪重比限值要求；若前三阶振型结构基本周期远大于5Tg，此时要满足规范设计剪重比限制要求，可能需要调整结构体系和总体布置，以便计算剪重比接近设计剪重比。

⑶ 规范剪重比限制与场地特征周期无关，特征周期越小，越难满足规范设计剪重比，特征周期越大，反而更容易满足设计剪重比，因此可能造成场地条件好的建筑结构，剪重比控制过于严格，场地条件越差的建筑结构剪重比控制过松。建议文献[1]规范编制组，考虑设计剪重比与场地类别挂钩，场地类别越好，设计剪重比限值取小，场地类别越差，设计剪重比限值取大。

⑷体型规整的建筑结构不容易满足设计剪重比，体型不规则的建筑结构反而更容易满足设计剪重比，与我们建筑设计应优先选用规则的形体的设计原则相违背，其他设计参数指标均满足规范要求的前提下，是否可以考虑剪重比不满足规范剪重比时，均可通过乘以增大系数方法来处理。

⑸第1、第2 平动周期扭振成分控制在10%以内，位移比控制在1.2 以内，其他参数指标满足规范要求，此时计算剪重比接近规范设计剪重比，说明结构布置、结构刚度趋于合理。