基于蜻蜓-高斯过程回归耦合的居民社区时用水量动态实时区间预测

刘龙龙，李文竹，刘 心

(1.河北工程大学，河北 邯郸 056038；2.邯郸河务局，河北 邯郸 056001)

我国水资源存在的时空分布不均、用水矛盾突出等现实问题，越来越成为新时期经济社会发展的制约性因素[1]。水资源日益短缺，对区域水资源进行合理规划、利用和调度势在必行。居民社区用水是水资源消耗的重要组成部分[2]。科学的管网调度能节省大量的供水消耗，全面提高管网的安全性和可靠性，但调度方案是否可行很大程度上取决于用水量的预测精度[3]。

对用水量预测方法的研究一直是国内外学者研究的热点，主要有以时间序列法为代表的传统方法、以人工神经网络(ANN)为代表的人工智能方法和以支持向量机(SVM)为代表的机器学习算法[4]。然而这些方法都只能得到确定的点预测结果和未来某一时刻的预测结果，而居民实际用水量蕴含各种不确定性因素，点预测结果必然存在不同程度的误差，进而使调度决策工作面临一定程度的风险。另外，如果预测的结果不是实时的，仅是未来某一时刻的值，那么调度人员无法根据准确的时用水量值进行实时调度。如果能够给出实时预测结果和其变化区间，使调度决策人员随时了解未来用水量的变化波动范围，有利于其做出更合理的决策。

高斯过程回归(GPR)是通过寻找训练数据之间的关系来进行系统辨识的一种非参数黑箱模型,是用于概率问题预测建模的一种强大工具[5]。与ANN和SVM方法相比，GPR不仅能够预测未知量的期望值，还能给出其分布状况,同时也能进行实时预测。此外，GPR模型参数较少、易实现和泛化能力强等优点[6]，可以直接方便的用于区间预测和实时预测[7]。通常采用共轭梯度法求解最优超参数，但存在优化效果对初始值依赖性强和容易陷入局部最优的缺点。

蜻蜓算法是美国学者MIRJALILI S在2015年提出的一种基于种群的启发式智能优化算法[8]。自然界中的蜻蜓生活方式包括静态和动态群体行为，这和启发式优化算法中的两个重要阶段探索和开发非常类似[9]。蜻蜓算法通过模拟蜻蜓群体航行、捕食及躲避外敌等行为进行全局和局部搜索，寻找猎物的过程就是算法寻优的过程[10,11]。本文提出用擅长全局搜索和对初始值没有依赖的蜻蜓算法进行超参数寻优，形成蜻蜓-高斯过程回归耦合算法(DA-GPR)，对居民社区时用水量进行动态实时区间预测。

1 蜻蜓-高斯过程回归耦合预测模型

本文通过高斯过程回归与蜻蜓算法的有机结合，利用擅长全局搜索和对初始值没有依赖的蜻蜓算法进行最优超参数寻优，并利用高斯过程回归(GPR)寻找时用水量训练数据之间的关系来进行系统辨识,给出其分布状况,对居民社区时用水量进行动态实时区间预测。

1.1 DA-GPR基本原理

从函数空间角度来看，高斯过程回归其性质由均值函数m(x)和协方差函数k(x,x′)确定[12]，定义为：

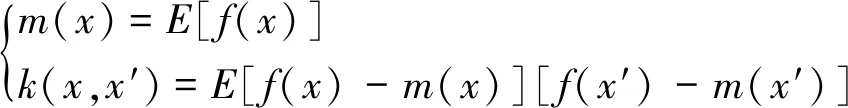
(1)

式中：函数f(x)的高斯过程(Gaussian process,GP)数学表达式为f(x)～GP[m(x),k(x,x′)],x,x′∈Rd是任意的随机变量。

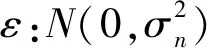
(2)

式中：K(X,X)=Kn=(kij)为n×n阶对称正定协方差矩阵。

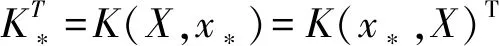
预测值的后验分布为：

(3)

(4)

(5)

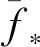
本文的协方差函数采用平方指数协方差函数，为：

(6)

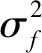
1.2 DA-GPR目标函数设计

蜻蜓-高斯过程回归耦合时用水量预测模型的最终目标是对未来的时用水量进行较准确的动态实时区间预测，并具有较好的泛化能力。因此在使用蜻蜓算法优化高斯过程回归的参数时，选取能充分代表泛化能力的目标函数是非常重要的。常规的蜻蜓优化算法将训练集上获得最小平均相对误差(MAPE)的参数作为最优解。即，将训练集上获得最小平均相对误差(MAPE)作为目标函数，对蜻蜓个体进行选着，目标函数值越小，蜻蜓个体越优，对应的参数越优，目标函数的选着至关重要。

居民社区每小时的用水量比较少，基本上在几立方米到十几立方米，仅仅采用平均相对误差(MAPE)作为目标函数值进行参数寻优的效果不理想。在此基础上，本文对DA-GPR进行改进，将体现绝对误差大小的平均绝对误差(MAE)和均方误差(MSE)引入到目标函数中，将平均相对误差(MAPE)、平均绝对误差(MAE)和均方误差(MSE)进行线性组合，构造出新的目标函数，如下式所示。

F(x)=3MAPE+2MAE+MSE

(7)

1.3 DA-GPR局部搜索公式设计

蜻蜓群体在一个小的区域内来回飞翔寻找猎物以及躲避外敌。通过模拟蜻蜓群体之间寻找猎物以及躲避外敌的社会互动行为来实现优化的过程，就是算法的局部搜索过程。

蜻蜓个体在群体运动中可以分为分离、对齐、内聚、食物吸引和天敌排斥等5种行为模式。该行为的具体意义和数学表达方法如下[13]。

(1)分离：指蜻蜓与相邻个体之间避免碰撞。该行为的计算公式如下:

(8)

(2)对齐：指相邻个体之间倾向于保持相同的速度。该行为的计算公式如下:

(9)

(3)内聚：指蜻蜓个体试图向自己认为所属的群体靠近。该行为的计算公式如下:

(10)

(4)食物吸引力：指食物对蜻蜓的吸引力。该行为的计算公式如下:

Fi=X+-X

(11)

(5)天敌排斥力：指蜻蜓对天敌的排斥力。该行为的计算公式如下:

Ei=X-+X

(12)

式中：Si为第i个个体的分离量；X为当前个体的位置；Xj为相邻个体j的位置；N为相邻个体的数量；Ai为第i个个体的对齐量；Vj为第j个邻近个体的速度；Ci为第i个个体的内聚量；Fi为第i个个体对猎物的吸引力；X+为猎物所在的位置；Ei为第i个个体需逃离天敌的距离；X-为天敌所在的位置。

1.4 DA-GPR全局搜索公式设计

在蜻蜓寻优的过程中，大量的蜻蜓群体朝着同一个方向进行长距离迁移，这个群体活动就是对算法的全局搜索过程。

根据5种蜻蜓行为，下一代蜻蜓的步长计算如下：

ΔXt+1=(sSi+aAi+cCi+fFi+eEi)+ωΔXt

(13)

有邻近蜻蜓时，下一代蜻蜓的位置为：

Xt+1=Xt+ΔXt+1

(14)

无邻近蜻蜓时，设置为随机游走(Le′xy飞行)行为，下一代蜻蜓的个体位置为:

Xt+1=Xt+Le′xy(d)×Xt

(15)

式中：t为当前迭代次数；i为第i个蜻蜓个体；Xi为当前第t代种群个体位置；ΔXt+1为下一代种群位置更新步长；Xt+1为下一代种群个体位置；s，a，c，f，e分别对应于5种行为的权重；ω为惯性权重；d为个体位置向量的维数。

Le′vy函数计算公式如下：

(16)

(17)

式中：r1，r2为[0,1]随机数；Γ(x)=(x-1)!；β是一个常数(这里取为0.5)。

蜻蜓算法在寻优的过程中，对每个个体的邻近个体数量的计算是非常重要的，因此这里假定一个邻域半径，该半径随迭代次数的增加而成比例地增长。同时，为了达到算法的局部搜索和全局搜索的平衡，权重(s，a，c，f，e和ω)在优化过程中自适应地调整。

1.5 DA-GPR算法步骤

流程图如图1所示。

图1 DA-GPR模型区间预测流程图Fig.1 DA-GPR model interval prediction flow chart

具体实现步骤如下：

Step1：读取样本数据，产生训练集和测试集。

Step2：初始参数设置：设置蜻蜓种群规模、最大迭代次数和参数l,σf,σn的取值范围。

Step3：初始化蜻蜓：随机初始化蜻蜓的位置H、步长ΔH、邻域半径R，惯性权重ω，分离权重s，对齐权重a，内聚权重c，食物吸引权重f，天敌排斥权重e。

Step4：将蜻蜓个体位置H的信息依次赋值给l,σf,σn。其中位置H矩阵的第一行存放参数l的值，第二行存放参数σf的值，第三行存放参数σn的值，每个蜻蜓个体对应一组参数值。

Step5：创建GPR模型，对训练样本进行训练，求出每组参数对应的目标函数值，并将其作为蜻蜓算法的适应度函数值，判断当前的适应度函数值是否为最佳适应度值，若是则将对应的超参数保存为最优超参数值,否则仍保存原适应度值及其所对应的参数值。

Step6：判断是否达到最大迭代次数，如果达到最大迭代次数，则输出最优超参数并创建最优的GPR模型；如果达不到最大迭代次数，则依次更新蜻蜓最优个体和最差个体、更新邻域半径、更新个体位置，然后返回步骤Step4继续迭代。

Step7：将测试集数据输入创建的最优GPR模型，输出预测值的均值和方差。

Step8：根据给定置信度，得到时用水量实时区间预测结果。

2 仿真实验

2.1 仿真实验平台

本次实验的运行环境为：操作系统：Windows 7；处理器：Intel(R) Core(TM)i7-2640M；主频：2.80GHz；内存：4.00GB；编程工具：MATLAB R2015(b)。

2.2 样本数据

本文所用的数据来自河北工程大学在线水量检测平台，采用居民家属院2016年6月17日到7月7日，共21 d每天24 h的实际社区时用水量资料，如图2所示。将样本集21 d/h用水量中的前20 d 480组时用水量资料作为训练集，最后一天24 h用水量资料作为测试集。

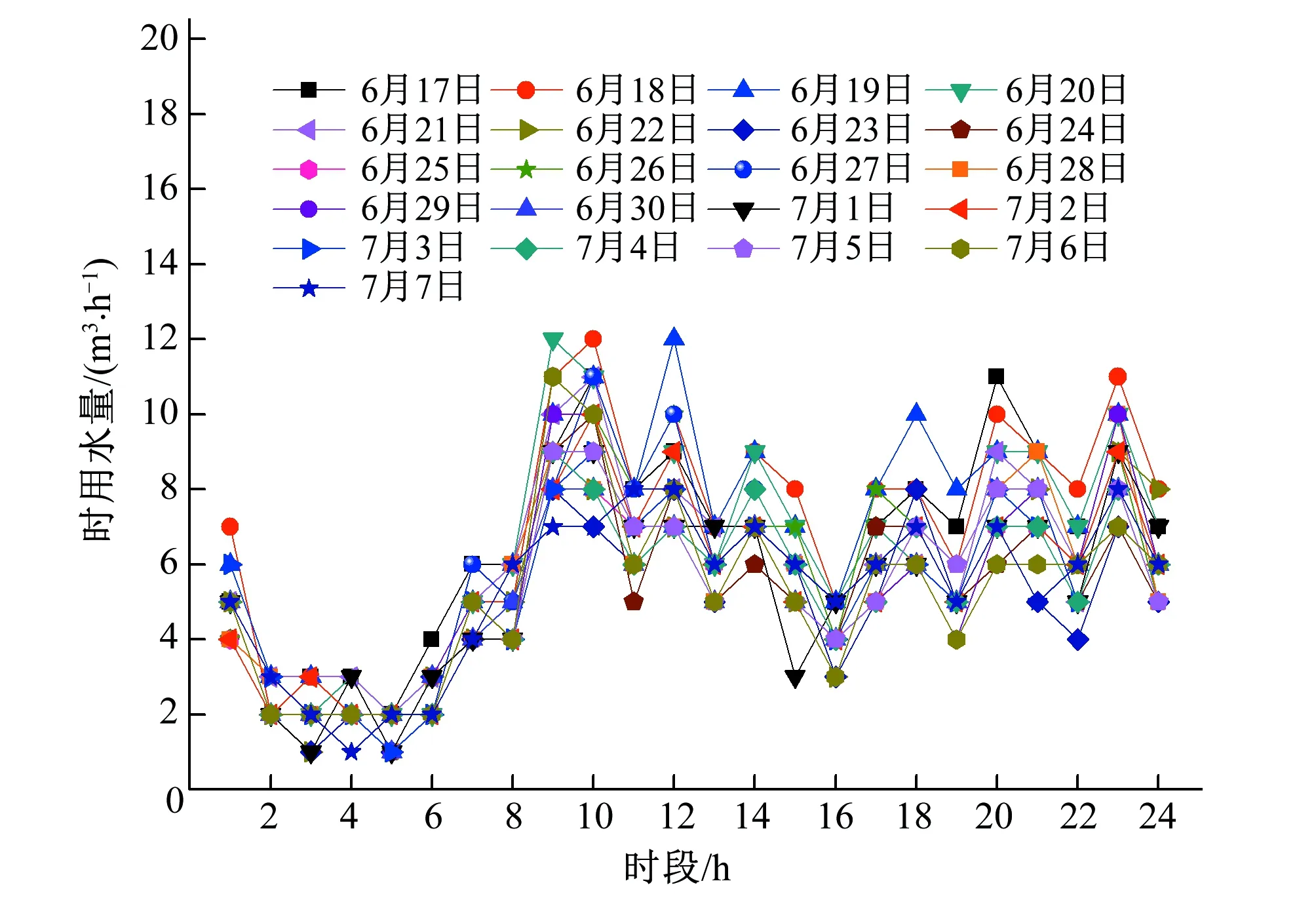
图2 单日时用水量变化趋势Fig.2 Change in water consumption on a single day

2.3 模型输入和输出

从图3可以明显看出居民社区时用水量具有明显的24 h周期性，为预测下一时刻用水量，模型的输入取该时刻前24 h的时用水量。模型输出是居民社区下一时刻用水量，输入是该时刻前24 h每小时用水量(数据来源于2016年6月17日到7月6日居民社区的用水数据)。

图3 不同模型时用水量预测结果Fig.3 Water consumption prediction results of different models

2.4 参数设置

惯性权重ω、分离权重s、对齐权重a、内聚权重c、食物吸引权重f和天敌排斥权重e均为自适应线性递减权重，其最小值为0.4，最大值为0.9；设种群规模为10，最大迭代次数为20，参数M的取值范围为[-1，1]，参数σf的取值范围为[-1，1]，参数σn的取值范围为[-1，1]。

2.5 对比模型及评价标准

为了使DA-GPR模型的预测结果具有可比性，选着BP神经网络、最小二乘支持向量机和高斯过程回归模型作为对比模型，模型性能采用平均相对误差(MAPE)、平均绝对误差(MAE)和均方误差(MSE)进行衡量，它们的定义为：

(18)

(19)

(20)

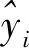
2.6 结果与分析

为了验证本文创建的蜻蜓-高斯过程回归耦合模型的预测可靠性，本文将其与BP神经网络、最小二乘支持向量机和高斯过程回归预测模型进行试验对比，预测结果如图3所示。在95%置信度下，高斯过程回归和蜻蜓-高斯过程回归两个模型的区间预测结果如图4和图5所示。从图3可知，BP神经网络和最小二乘支持向量机模型预测结果误差较大，蜻蜓-高斯过程回归模型预测的结果误差较小。从图4可知，高斯过程回归模型预测的结果误差较大，极个别点落在了预测区间外。从图5可知，蜻蜓-高斯过程回归预测模型预测的结果走势与实测值一致，预测值与实测值基本上重合，误差较小。

图4 高斯过程回归(GPR)时用水量预测结果Fig.4 Water consumption prediction results in Gaussian process regression (GPR)

图5 蜻蜓-高斯过程回归(DA-GPR)时用水量预测结果Fig.5 Prediction of water consumption in the dragonfly Gauss process regression (DA-GPR)

不同预测模型的预测相对误差如图6所示。从图6可以看出，BP神经网络预测模型相对误差最大为0.5，最小二乘支持向量机预测模型相对误差最大为0.9，高斯过程回归预测模型相对误差最大为1.653，蜻蜓-高斯过程回归预测模型相对误差最大为0.019。显然，蜻蜓-高斯过程回归预测模型具有更高的预测精度。

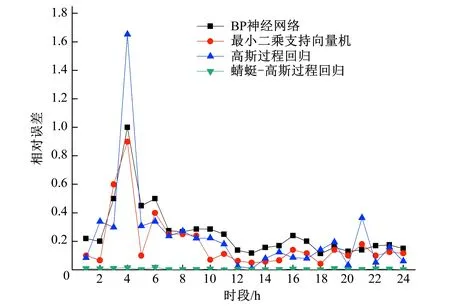
图6 不同预测模型预测的相对误差Fig.6 Relative error of prediction model of different prediction models

采用平均相对误差(MAPE)、平均绝对误差(MAE)和均方误差(MSE)对不同模型的预测结果进行分析，结果如表1所示。通过表1可以看出，蜻蜓-高斯过程回归模型的居民社区时用水量预测精度优于BP神经网络、最小二乘支持向量机和高斯过程回归模型，取得了较好的预测效果。

表1 不同预测模型误差分析Tab.1 Error analysis of different prediction models

3 结 语

居民社区时用水量具有较强的不确定性和随机性，传统的ANN、SVM等预测方法只能得到确定的点预测结果和未来某一时刻的预测结果，无法给出预测的区间，也不能进行实时预测。为了克服这些缺点，本文提出了一种基于蜻蜓-高斯过程回归耦合的居民社区时用水量动态实时区间预测方法。为进一步提高预测精度，进行了改进，最终得到了一定置信水平下的区间预测结果。仿真结果表明，本文构建的区间预测方法与常规方法相比，不仅能够预测未知量的期望值，还能给出其分布状况,同时也能进行实时预测。而且预测精度较高，最大的相对误差为仅0.019，具有较强的实用价值，为未来水资源实时调度提供理论依据。