改进人工蜂群算法在平板闸门控流中的应用

孔祥宇，贾敏智

(太原理工大学电气与动力工程学院，山西 太原 030024)

0 引 言

水是生命之源，是我们生产、生活中必不可少的资源，水对于人类的重要性不言而喻。随着我国农业的发展，农业生产用水量也在迅速增长，在农业生产中，灌溉用水量占总用水量的60%以上，而利用率却不足五成，水资源浪费较为严重，因此，必须对灌溉过程进行优化，以减少水资源的浪费。国内大部分的农田灌溉模式是渠道灌溉，渠道灌溉系统中，最重要的一环就是控制流量，若流量大小已知，便可根据时间计算水量。在使用步进电机实现的闸门开度控制系统中，步进电机对闸门的控制是离散的，步进电机转过一个角度，对应的闸门增加一定的开度，因此，找到一个合适的闸门开度，以使得闸门流量最接近于给定的流量，成为了一个寻求最优解的过程。

1 流量计算数学模型

矩形平板闸门具有占地面积小、驱动功耗低、安装方便等优点，性价比高，非常适合在各型灌区中使用。根据明渠测流理论，矩形平板闸门通过调节闸门开度来调节流量，当闸门开度与闸门上游水位之比e/H≤0.65时，属于闸孔出流状态；当e/H>0.65时，属于堰流状态。闸孔出流状态又分为自由出流和淹没出流，如果下游水位不影响射流，为自由出流，否则，为淹没出流[1]。

收缩断面的跃后共轭水深计算公式为：

(1)

(2)

hc=eε

(3)

(4)

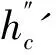
闸孔自由出流状态下的流量计算公式为：

(5)

(6)

式中：μ0为流量系数；b为闸门宽度。

闸孔淹没出流状态下的流量计算公式为：

(7)

(8)

(9)

式中：ht为闸门下游液位；φ为流速系数，取0.97。

堰流出流状态下的流量公式为：

(10)

(11)

(12)

式中：ha为堰上水头；σ为淹没系数；m0为流量系数；a为堰高，闸门安装好后a为固定值[2]。

从公式(1)到公式(12)可以看出，除了堰流状态，自由出流状态和淹没出流状态对于流量Q的计算均和闸门开度e相关。因此，只有选择合适的阀门开度，使得流量达到给定值，才能更加精确地控水，从而达到节约用水的目的[3]。

2 算法原理和应用

2.1 反向学习的定义及相关内容

反向数：设x∈[a,b],且为实数，则反向数的定义为：

x*=a+b-x

(13)

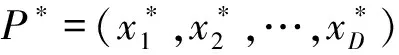
(14)

一般反向学习(Generalized Opposition-Based Learning, GOBL)：设x是当前搜索空间[a,b]中的一个解，新解x*以如下方式定义：

x*=Δ-x

(15)

式中：Δ是一个可计算的值，x∈[Δ-b,Δ-a]。同理，D维搜索空间的一般反向学习可定义为：

(16)

式中：i∈(1,2,…,D)。运用一般反向学习，我们不但可以评估当前候选解x，还可以计算评估其转换解x*。这使得找到或接近最优解的可能性大大增加。设Δ=k(a+b),k为实数，则一般反向学习的具体形式为：

x*=k(a+b)-x

(17)

根据k值的不同，我们有四种不同的GOBL模式。我们这里取k=rand(0,1)，即k为[0,1]之间的随机数。这个模式的定义为：

x*=rand(0,1)(a+b)-x

(18)

这种模式生成的反向种群与正向种群相结合，全局性更强，减小了局部最优的发生概率，更容易找到最优解。

2.2 人工蜂群算法的基本原理

人工蜂群算法(ABC)是模拟蜜蜂的采蜜行为得出的算法。ABC算法将人工蜂群分为3类：雇佣蜂，跟随蜂和侦查蜂，雇佣蜂和跟随蜂对食物源进行开采，侦察蜂是为了防止食物源种类过少。雇佣蜂和跟随蜂各占蜜蜂种群的一半，雇佣蜂的数量和食物源的数量相等，即一处食物源对应一只雇佣蜂。如果某个食物源被雇佣蜂和跟随蜂放弃，那么这个食物源对应的雇佣蜂变为侦察蜂[4-6]。在ABC算法中，每个食物源代表优化问题的一个可行解，每个食物源的蜜量代表一个解的适应度。

(1)初始化。首先，初始化蜂群数量NP,食物源数量NP/2(即ABC算法根据公式(19)随机产生NP/2个初始解)。

xi,j=xmin,j+rand(0,1)(xmax,j-xmin,j)

(19)

式中：xi,j表示第i个解的第j维值；xmax,j，xmin,j分别表示第j维搜索空间的上下界，且1≤i≤NP/2,j∈{1,2,…，D}，D是解的维度。

(2)雇佣蜂阶段。初始化完成后，蜜蜂开始对所有的初始解进行循环搜索，雇佣蜂会根据公式(20)，对记忆中的食物源进行改变产生一个新的食物源(即产生一个新的可行解)，并根据公式(21)计算新食物源的蜜量(即新解的适应度)，现实中的蜜蜂则是对原来食物源周围的其他食物源的视觉信息进行比较来发现新的食物源。如果新食物源的蜜量高于原来的食物源，那么雇佣蜂将记忆中原来的食物源替换为新的食物源(即用新解替换旧解)。

vi,j=xi,j+δi,j(xi,j-xk,j)

(20)

式中：δi,j为[-1,1]之间的随机数,k∈{1,2,…,NP/2}，为不同于i的整数；vi,j是产生的新的可行解。

(21)

式中：f(xi)为第i个解的目标函数值；fiti是第i个解的适应度值。

雇佣蜂完成搜索后回到蜂巢，将所获取的食物源信息与跟随蜂共享。

(3)跟随蜂阶段。跟随蜂对雇佣蜂搜索到的食物源的信息进行评估，按照公式(22)计算出来的概率选择一个食物源。然后，跟随蜂同雇佣蜂一样，对记忆中的食物源进行修正，若新修正的食物源的蜜量高于原来的食物源，那么就用新食物源来代替记忆中的旧的食物源。否则，保持对原来食物源的记忆。

跟随蜂对食物源的选择根据食物源蜜量相关的概率来进行，概率的公式为：

(22)

式中：fitmax为所有解的最大适应度值；pi为第i个解对应的概率。

(4)侦查蜂阶段。搜索过程中，如果食物源xi经过t次检验，且达到上限值limit，但是没有找到更好的食物源，则该食物源会被舍弃，依据公式(19)产生新的食物源。

(5)输出最优解。在完成以上三步后，如果达到终止条件，那么就可以输出最优解，见图1。

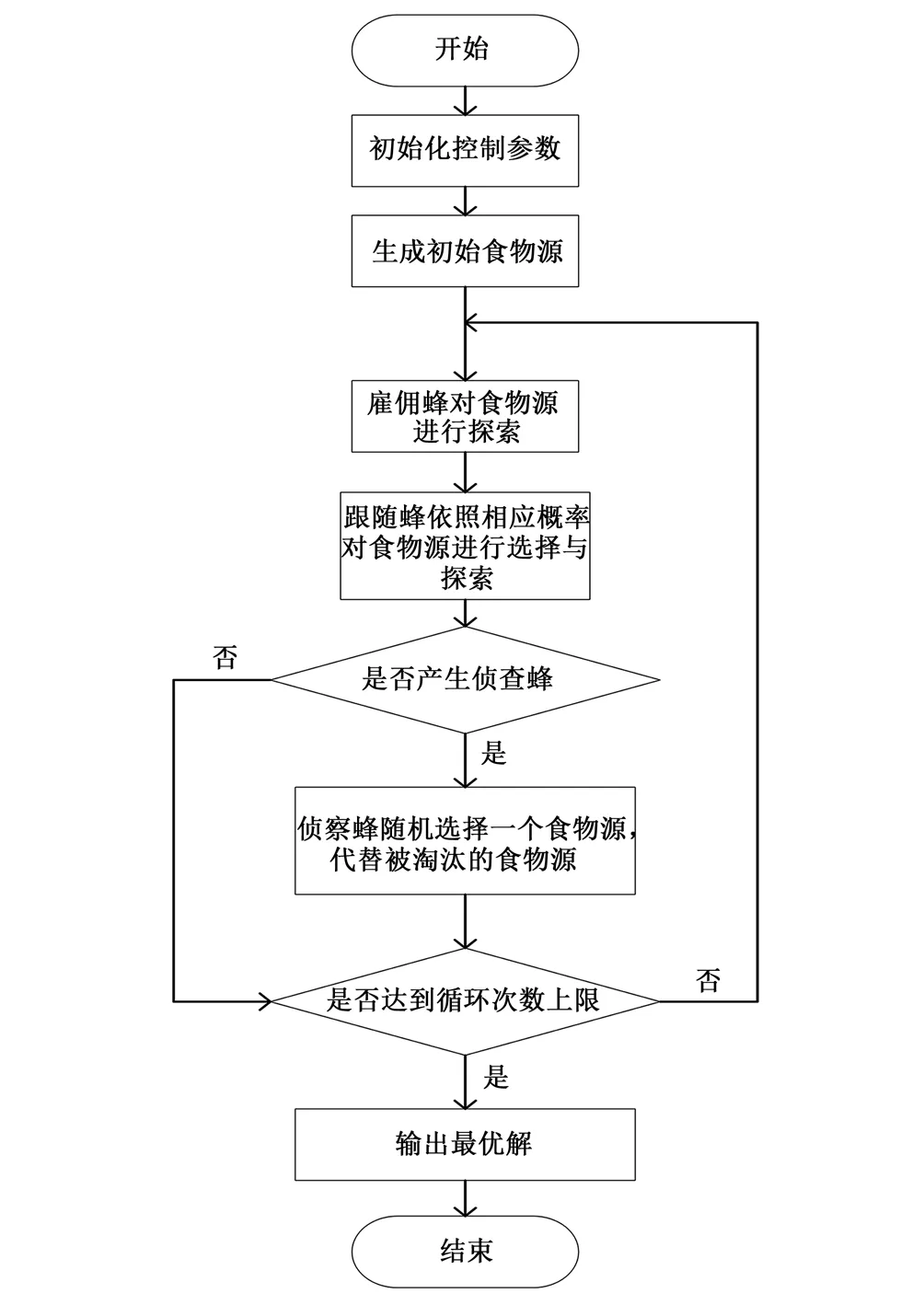
图1 人工蜂群算法流程图

2.3 引入反向学习的人工蜂群算法

由以上可知，将反向学习运用于人工蜂群算法的食物源初始化阶段，可以使得食物源的多样性得到提高，更有利于寻找最优解。反向食物源的公式为：

(23)

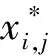
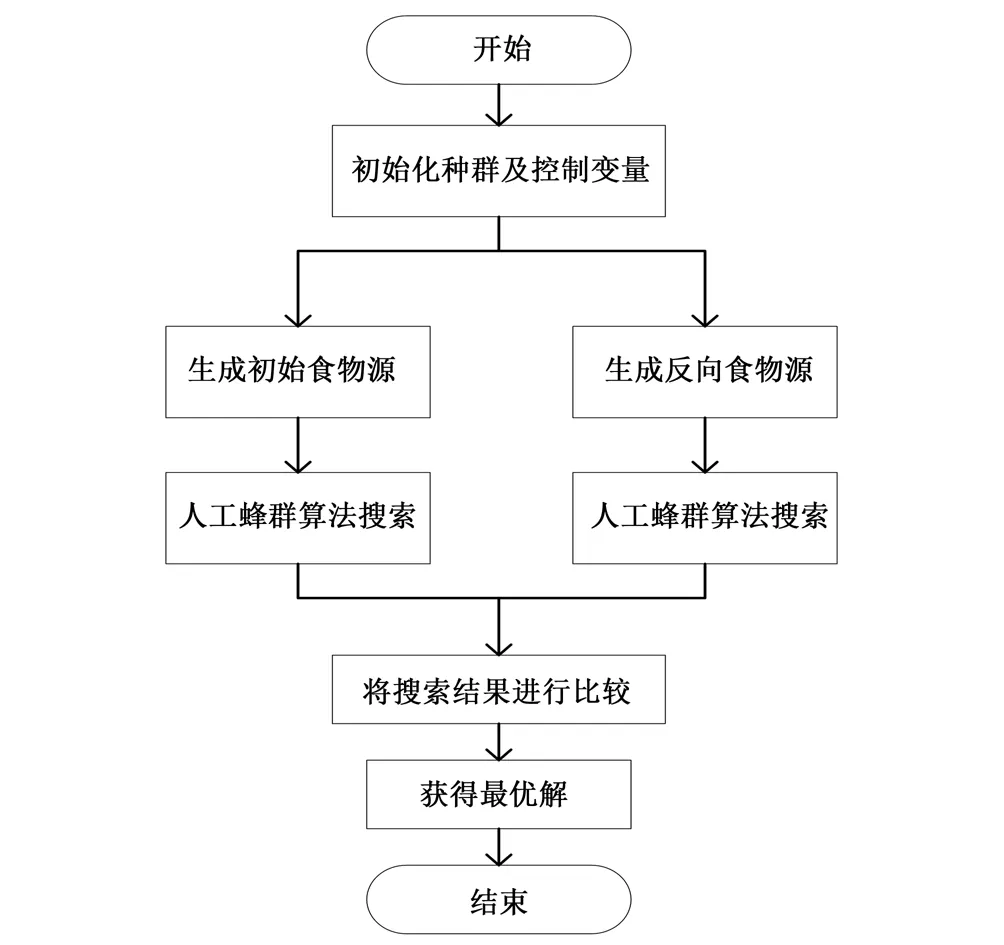
图2 引入反向学习的算法流程

利用人工蜂群算法对正向食物源进行搜索的同时，对反向食物源也进行搜索，再对正、反向食物源中的最优解进行比较，从而选择出最终的最优解。

3 算法应用及数据结果分析

3.1 将反向人工蜂群算法运用于闸门开度计算

根据公式(5)和公式(7)来计算自由出流状态和淹没出流状态下的短时间内的流量。通过不停地调节闸门开度的大小，使闸门的流量趋于稳定，让其达到所需求的流量大小。可以将给定流量Q0和计算流量Q之差ΔQ作为一个约束条件，作为目标函数，求得目标函数的最小值，同时求得此时对应的参数，即最优闸门开度。

已知某渠道分水闸门的开度范围设置为:0～0.3 m，闸门宽度为:0.5 m，闸门上游液位为0.8 m，闸门下游液位为0.4 m，这时的流态为闸孔出流状态。根据流态判断的流程，闸门开度在0～0.16 m时，流态为淹没出流，在0.16～0.3 m的范围内时，为自由出流，见图3。

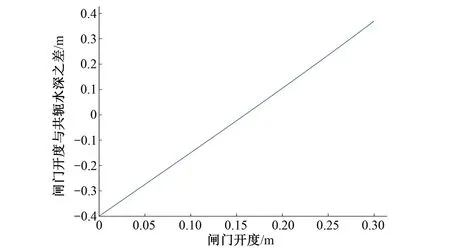
图3 共轭水深与闸门下游液位的差同闸门开度的关系图

在闸门上、下游液位和闸门的开度已知时，闸门流量的范围就可以得到。因此，只要用户在对应区间内设定流量大小，便可以通过调节闸门开度实现。为了求得此时的最优闸门开度，我们采用引入反向学习的人工蜂群算法来计算。在这里我们能够设定的需求流量大小，是根据上下游的水位变化的，系统会给出一个合理的范围，在这个范围内设定所需流量，才能通过调节闸门开度实现。

当闸门上游液位为0.8 m的时候，在淹没出流状态下，闸门所能控制的流量大小范围为：0～0.14 m3/s；在自由出流状态下，闸门所能控制的流量大小范围为：0.18～0.31 m3/s，见图4。

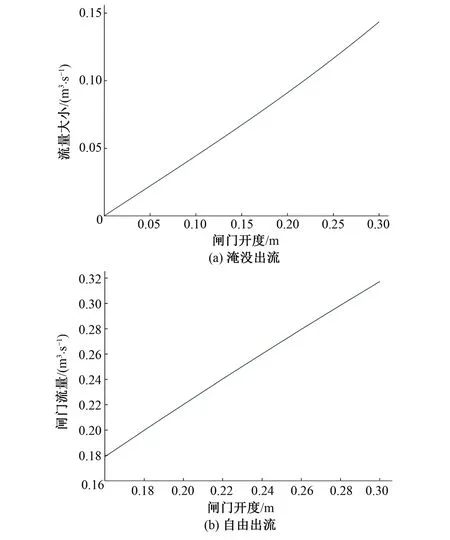
图4 闸门开度同闸门流量关系图

在闸孔出流流态下，运用引入反向学习的人工蜂群算法在10次迭代左右便找到了最优解，使得计算流量与给定流量差约等于0，这样的收敛速度完全符合要求，见图5和图6。

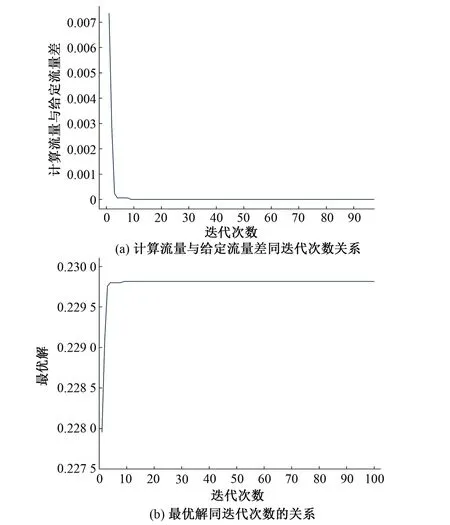
图5 迭代次数同计算结果的关系(Q0=0.25 m3/s)

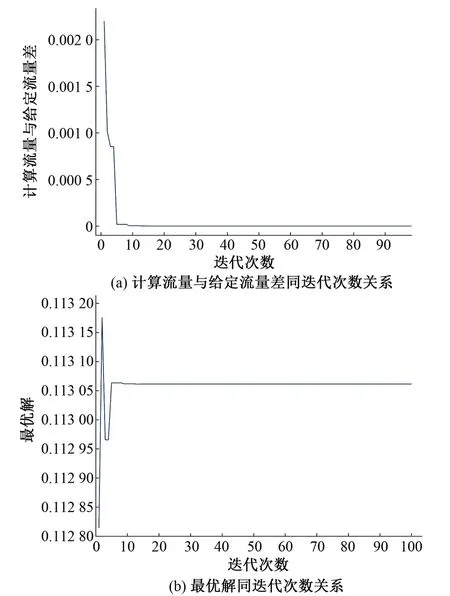
图6 迭代次数同计算结果的关系(Q0=0.1 m3/s)

当闸门上游液位0.8 m，闸门宽度0.5 m，闸门下游液位0.4 m时，为达到不同的给定流量Q0，通过所得的最优闸门开度e求得计算流量Q，可以看出计算流量与给定流量的绝对误差都小于1%，本文所用算法的计算精度符合要求，见表1。

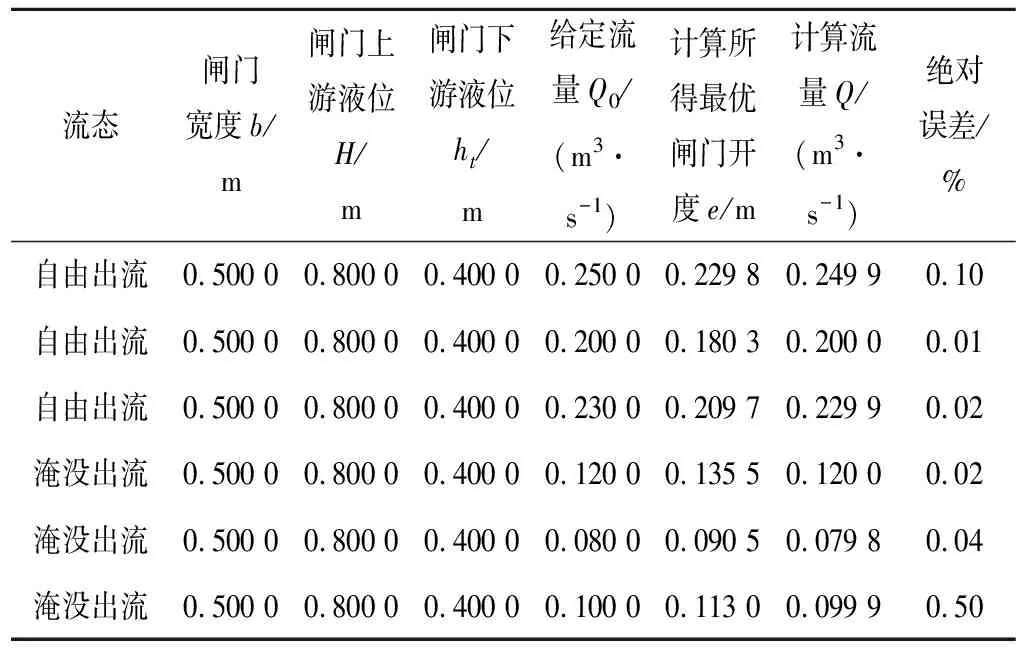
表1 计算流量与给定流量相关数据统计

3.3 与其他算法的比较

同上面自由出流的条件相同，这次采用粒子群算法来求最优解。

当闸门上游液位为0.8 m的时候，在自由出流状态下，闸门所能控制的流量大小范围为：0.18～0.31 m3/s，将给定流量设置为0.25 m3/s，此给定流量在自由出流的流量范围内，此时，闸门为自由出流状态。通过使用粒子群算法，求得在自由出流状态下，达到给定流量的闸门最优开度为 0.23 m。在使用普通粒子群算法进行计算时，迭代接近40次才能找到最优解，而人工蜂群算法只需要10次左右便可得到，粒子群算法的收敛速度不如引入反向学习的人工蜂群算法，见图7。

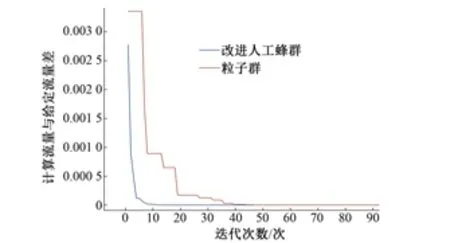
图7 两种算法的比较

在自由出流状态下，通过粒子群算法和引入反向学习的人工蜂群算法的求解过程进行比较发现，引入反向学习的人工蜂群算法的收敛速度更快，精准度更高。

4 结 语

我国的水资源并不丰富，在渠道灌溉占大多数的情况下，节约用水是不变的主题，分水闸门的流量控制是渠道灌溉的关键，控制了流量，便控制了水量。在分水闸门流量控制的过程中，为了达到所要求的流量大小，控制闸门开度是主要的解决方法。实际操作中，技术人员根据土壤湿度，来确定一定面积的农田需要灌溉的水量，控制系统根据所需要的水量，根据当前的条件计算出合适的给定流量Q0，再通过调节闸门实现 。本文采用了能够准确计算闸门开度的基于反向学习的人工蜂群算法，该算法的收敛速度和计算精度都满足闸门开度计算的需求，在不同的闸门出流条件下，计算出相关的闸门开度大小，并根据实时液位变化进行计算和调节，使得闸门流量保持稳定。知道了闸门流量的大小，便可通过时间计算出流出的水量，更好地节约用水。