弧面分度凸轮机构动态特性的研究

刘 超 何雪明 黄海楠 陈小飞

(1. 江南大学江苏省食品先进制造装备技术重点实验室，江苏 无锡 214122；2. 三一重机有限公司，江苏 苏州 215300)

弧面分度凸轮机构因具有结构简单，精度高，分度性能良好等优势，被广泛地应用于间歇分度机械中，尤其是在一些食品包装机械中，包括饮料罐装机、旋盖机等。为了提高这些机械运作的精度，分析动力学性能是提高机械运作精度的重点。Taylor等[1]通过赫兹接触理论计算出凸轮系统当中线接触和点接触的接触刚度，并计算了时频内的动态运动方程和应力情况，又在滑动接触的条件之下，分析并比较了凸轮机构中非线性和摩擦特性情况。张兴钰等[2]考虑到弹性变形、弯曲和扭转等因素对弧面分度凸轮机构的影响，整合刚柔耦合动力学相关的理论，通过UG、ADAMS、ANSYS 3个建模和工程分析软件建立凸轮机构的刚柔耦合动力学模型，并通过仿真分析阐述了不同因素对整个弧面分度凸轮机构动态特性的影响情况。冯立艳等[3]先利用ADAMS对已建好的弧面分度凸轮机构模型进行刚柔耦合运动学仿真分析，以此来验证该模型的正确性，再对该机构处在不同机构参数下进行动力学仿真分析，从而获取不同参数情况下主从动件之间接触力的变化曲线图。刘言松等[4]通过虚拟样机技术和多体动力学理论对弧面分度凸轮机构进行动力学仿真分析，这为后续凸轮机构的动力学研究创造了一种新的途径与方法。Livija[5]将主从件的柔性、整个机构当中非线性和阻尼等因素考虑进去，构造出凸轮、从动件及驱动轴系统集成一体的凸轮机构模型，以此来分析其动力学特性情况，并验证分析了从动件的稳定性及逼进稳定情况的条件。为了得到精确的弧面分度凸轮机构运动仿真结果，必须考虑构件的柔性条件。因此，如何建立合适的分析模型一直是实现该机构刚柔耦合运动仿真的核心问题。本研究拟基于虚拟样机技术，在ADAMS软件的基础上结合ANSYS软件建立刚柔耦合动力学模型，通过对该模型设置不同的凸轮转速、阻尼等运动参数，进一步分析其角速度、角加速度和接触力等运动性能的响应情况，旨在为该机构后续的动力学建模、动力学优化等研究提供参考。

1 弧面分度凸轮机构的建模

弧面分度凸轮机构在建模过程中，先需要对弧面分度凸轮的运动参数及几何机构参数进行确定，再利用双三次样条曲面算法重构出弧面分度凸轮的轮廓面；然后在此基础上，根据已知的参数对弧面分度凸轮、主动轴、分度盘、滚子、从动轴及载荷盘6个部件进行三维建模，并完成整个部件的装配。

1.1 弧面分度凸轮三维模型的建立

弧面分度凸轮的主要设计参数如表1所示，根据其具体参数可完成弧面分度凸轮模型的建立。

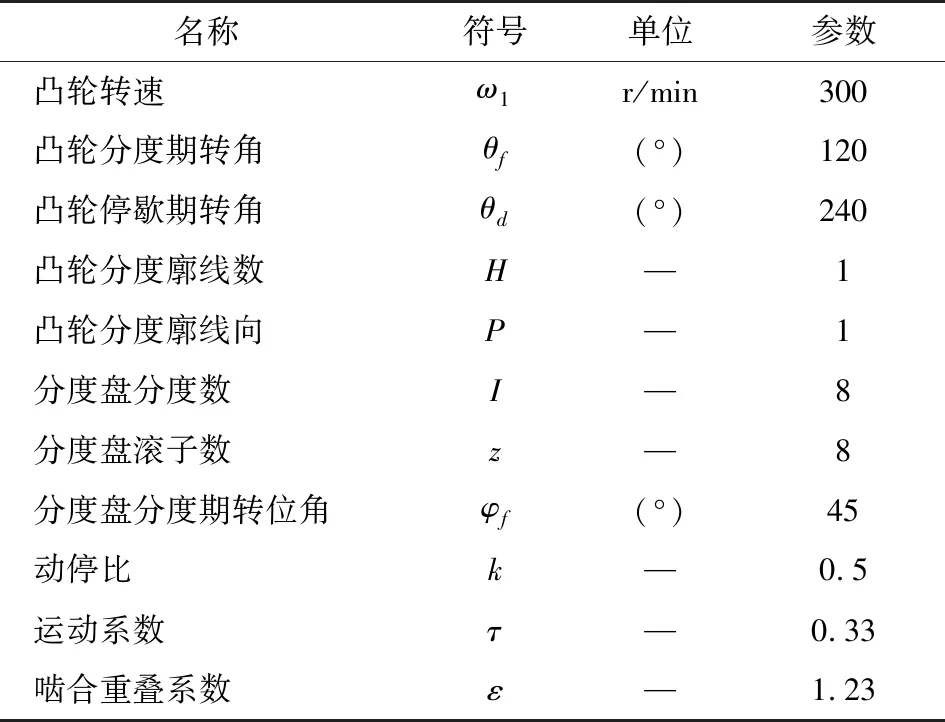
表1 弧面分度凸轮机构的运动参数

弧面分度凸轮具体建模过程：根据表1中弧面分度凸轮机构参数，结合C++导出弧面分度轮廓面的设计模块，输入其相应的参数，即可生成分度期工作轮廓面的点云数据，再将点云数值保存为txt文件；通过轮廓面重构模块读取txt文件，通过样条曲面重构算法，显示出重构后弧面凸轮分度期重构面，将4个重构后的分度期曲面导出成IGES格式；当4个弧面分度凸轮轮廓面IGES格式文件分别导入UG后，在已有的4个弧面分度凸轮轮廓面的基础上，通过旋转命令完成2个弧面分度凸轮分度期曲面；在得到2个分度期面的基础上，根据表1的参数，对弧面分度凸轮进行建模、曲面合并、多余的工作轮廓面进行切除，再通过“旋转”“拉伸”等命令，便完成凸轮主体建模[6]。其实体模型如图1所示。

图1 弧面分度凸轮实体Figure 1 Body of globoidal indexing cam

1.2 弧面分度凸轮机构的装配

1.2.1 弧面分度凸轮机构三维模型的建立 完成弧面分度凸轮的建模，根据已知参数对弧面分度凸轮、主动轴、分度盘、滚子、从动轴以及载荷盘等6个部件进行三维建模，弧面分度凸轮机构的结构参数如表2所示；最后根据构造完成的三维模型，完成弧面分度凸轮机构的装配。

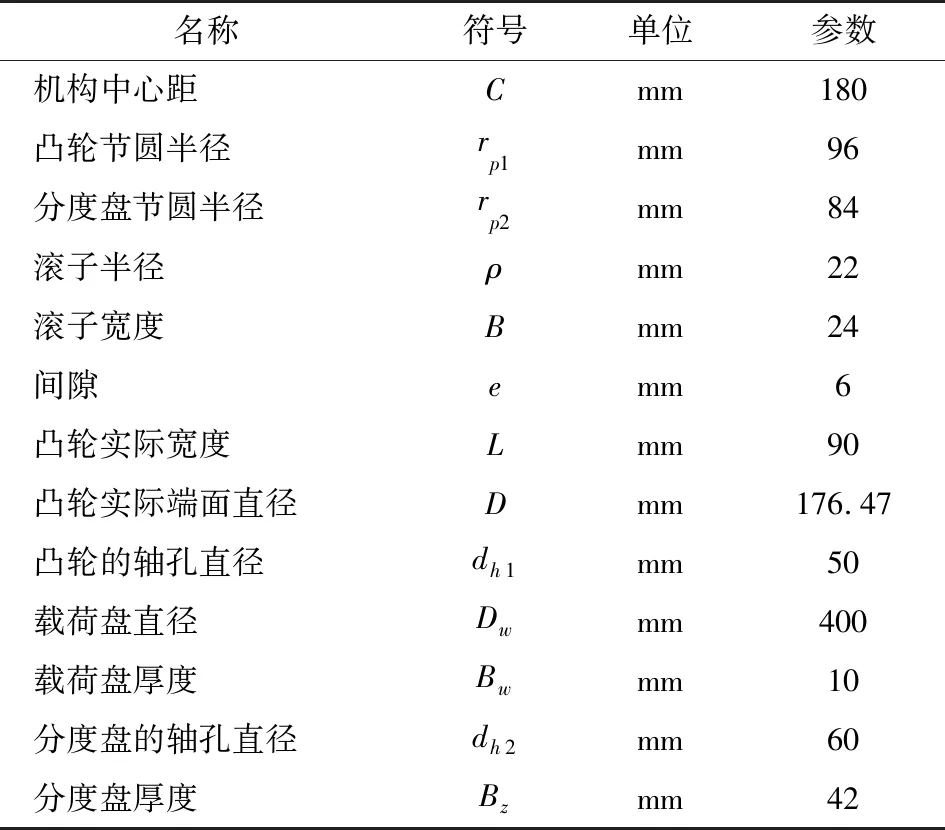
表2 弧面分度凸轮机构几何结构参数

1.2.2 弧面分度凸轮机构中各个部件的装配 弧面分度凸轮机构中部件的运动关系主要分为三类：固定连结关系、转动关系和共轭接触关系。

(1) 固定连结关系是指凸轮机构在工作过程中，2个零部件之间相对位置一直保持不变的关系。其中，输入轴与弧面分度凸轮，输出轴与分度盘，输出轴与载荷盘之间均为此种关系[7]。

(2) 转动关系是指2个零部件之间存在一定相对转动的关系。其中，输入轴与机架，输出轴与机架，各个滚子与分度盘均为此种关系。

(3) 共轭接触关系是指弧面分度凸轮与滚子之间所存在的相对运动关系。根据表2中的安装尺寸，完成整个弧面分度凸轮机构中各部件间装配关系。

根据以上弧面分度凸轮机构参数，完成了弧面分度凸轮机构中各个部件的装配之后，还需要干涉检测方法，检查整个弧面分度凸轮机构是否存在缺陷[8]。其各部件装配示意图如图2所示。

1. 滚子 2. 分度盘 3. 输入轴 4. 载荷盘 5. 弧面分度凸轮 6. 输出轴

图2 弧面分度凸轮机构的三维装配模型

Figure 2 3D assembly model of Globoidal Indexing Cam Mechanism

2 弧面分度凸轮机构运动特性分析与优化

2.1 弧面分度凸轮机构多刚体仿真模型的建立

研究重构后弧面分度轮廓面的动态特性，需对已经装配完毕的弧面分度凸轮机构模型进行运动仿真分析。将在UG中建立弧面分度凸轮机构的整个三维装配模型保存为“Parasolid”中间格式文件，导入到ADAMS软件中，得到整个弧面分度凸轮机构的动力学实体模型。

弧面分度凸轮仿真模型包括以下主要条件的设置：

(1) 环境的设定：对弧面分度凸轮机构所处的环境进行定义，主要包括重力场[9]。

(2) 材料属性设定：完成导入弧面分度凸轮机构模型之后，需要对弧面分度凸轮机构的各个部件材料进行设置。

(3) 约束关系的设定：输入轴和输出轴2个部件与大地之间建立旋转关系，输入轴与弧面分度凸轮之间建立固定约束关系，而输出轴与载荷盘和分度盘之间建立固定约束关系，8个滚子与分度盘之间也建立固定约束关系。

(4) 接触力的定义：由于接触关系，弧面分度凸轮在旋转过程中，与滚子之间产生一定的接触力，只有通过这两者之间的接触力才能实现分度盘的运转。因此，在弧面分度凸轮机构进行运动仿真分析过程之中，需要通过添加接触力来模拟与分析真实运转情况[10]。

在弧面分度凸轮机构运转过程中，从动件上各个滚子分别与弧面分度凸轮进行接触。因此，该2个零部件之间会有接触力，而弧面分度凸轮与滚子之间建立的接触关系为单次碰撞，则采用冲击函数法(Impact)显示更加合理。根据赫兹接触理论，阻尼对机构产生的能量损耗在总损耗能量所占的比例中是较小的。因此，取比较小的阻尼系数。

接触刚度按式(1)计算：

(1)

在式(1)中弹性模量E*按式(2)计算：

(2)

式中：

E*——弹性模量，N/mm2；

E1——凸轮的弹性模量，N/mm2；

μ1——泊松比；

E2——滚子的弹性模量，N/mm2；

μ2——泊松比。

当量半径按式(3)计算：

(3)

式中：

R1——凸轮当量半径，mm；

R2——滚子接触点的当量半径，mm。

取E1=2.12×105N/mm2，E2=2.19×105N/mm2；μ1=0.289，μ2=0.3，令R1=R2=22 mm，则计算出K=5.218×105N/mm。

在ADAMS界面中设定接触力，设置非线性指数为e=1.5，阻尼系数为C=60 N·s/mm，穿透深度为d=0.1 mm。具体参数设置，如图3所示。

(5) 驱动设定：在弧面分度凸轮和大地之间的旋转副上增加电机旋转的驱动，设置顺时针旋转，主动件的转速ω1=300 r/min=1 800 r/s。

通过以上5个步骤的参数设置，由此便完成了整个弧面分度凸轮机构的运动仿真模型的建立[11]。

2.2 弧面分度凸轮机构运动学仿真

在仿真前需要设定合理的参数，一方面，将驱动转速条件设定为300 r/min；另一方面，为了选用运动仿真的可靠性更好、计算精度更高的求解器。仿真完毕后，进入ADAMS后处理模块中查看仿真结果。为了校核重构之后弧面分度凸轮轮廓面的正确性，以分度盘作为研究对象，分析其运动规律是否符合理论值。同时，以分度期作为弧面分度凸轮主要研究过程，对仿真之后分度盘上角位移、角速度和角加速度与理论上修正正弦运动规律曲线进行对比与分析。

图3 ADAMS中Impact接触力设定Figure 3 Contact parameters setting

图4为多刚体模型的角位移、角速度和角加速度在ADAMS中的仿真结果，可以看出，在进入分度期后，角速度出现了轻微的波动，而角加速度的振动较为明显。但是，整体趋势与运动规律为修正正弦加速度相一致。所以，本研究中所建立的凸轮模型是正确的。

2.3 弧面分度凸轮刚柔耦合动力学模型创建

2.3.1 柔性体的建立 由于弧面分度凸轮机构多用于高精度、高转速的应用场合，属于比较复杂的多体变形系统。因此，为了让模型更加准确、仿真更精确，考虑到部件的弹性变形，需要建立弧面分度凸轮机构的刚柔耦合动力学模型。

弧面分度凸轮机构在高速运行并在接触力、惯性力及负载作用下，难免造成机构产生扭转变形、弯曲变形等，机构中输入轴和输出轴的影响最为明显。由于输入轴长度比较小，具有相对较大的刚度，可忽略其产生的弹性变形。因此，为了更好地研究弧面分度凸轮机构动态情况，本研究将弧面分度凸轮机构中输出轴视为柔性体，而其他部件视为刚性体。柔性体模型建立过程如图5所示。

(1) 将输出轴导出“.x_t”格式的中性文件。

(2) 将输出轴导入ANSYS当中，并按照表3设置材料属性；然后将其网格单元类型定义为三维8节点单元solid85，采用自由网格划分的方法来划分输出轴的网格，从而建立输出轴的有限元模型。

(3) 在输出轴与机架的旋转中心建立结点，以此作为外部结点与刚性构建的连接。同时划分刚性区域，将其导出成.mnf 中性格式文件。

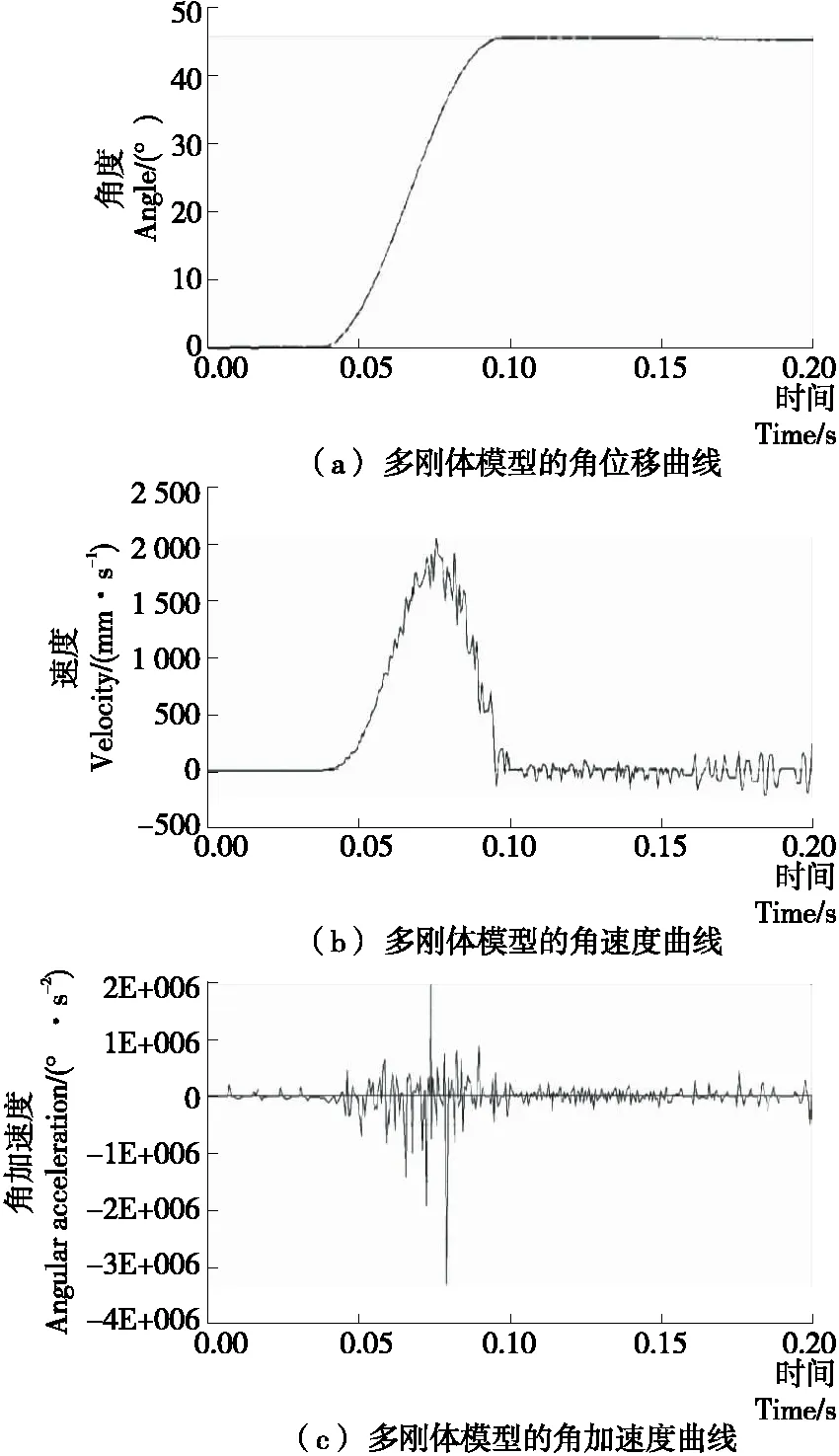
图4 弧面分度凸轮多刚体运动仿真分析结果Figure 4 Simulation results of multi rigid-body motion of globoidal indexing cam

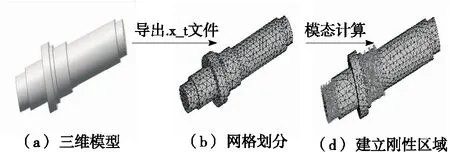
图5 输出轴柔性体建模过程Figure 5 Modeling process of output shaft flexible body

2.3.2 弧面分度凸轮刚柔耦合模型的建立 在原有运动仿真模型的基础上，先将输出轴替换为柔性体模型，然后删除原有的运动副约束，在输出轴上重新建立约束关系，从而完成刚柔耦合动力学模型的建立[12]，其刚柔耦合动力学模型如图6所示。

3 不同工况下弧面分度凸轮机构动态特性

在弧面分度凸轮机构从动件旋转过程当中，其速度会发生周期性的变化，尤其在高速工况下显得更为明显，主动件和从动件两部件之间将会产生动载荷的冲击。同时，还有其他因素将会对弧面分度凸轮机构的动态性能产生影响。而影响其动态性能的主要因素有以下几个：弧面凸轮机构结构参数、工况、加工精度和安装误差等。本试验重点研究转速和阻尼系数对弧面分度凸轮机构动态特性的影响。

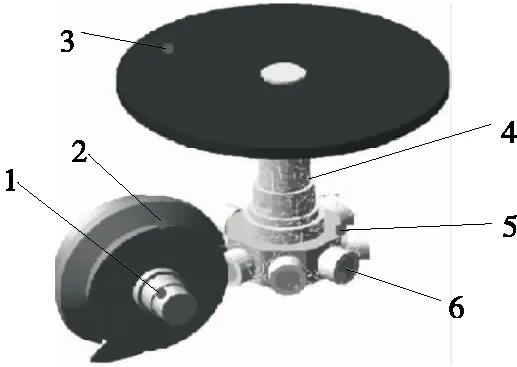
1. 输入轴 2. 弧面分度凸轮 3. 载荷盘 4. 输出轴 5. 分度盘 6. 滚子

图6 弧面分度凸轮机构刚柔耦合动力学仿真模型

Figure 6 Rigid-flexible coupling dynamic simulation model of globoidal indexing cam mechanism

3.1 转速对弧面分度凸轮机构动态性能的影响

为了满足不同转速工况下的要求，需根据具体应用场合设定相应的转速，载荷盘的厚度为10 mm，不考虑载荷盘上的载荷，设定转速为300，600，800，1 000 r/min，以此来分析弧面分度凸轮机构中不同转速对其自身动态性能(角加速度、接触力)的影响。

由图7、8可知，凸轮转速对整个机构的动态特性有显著的影响。尤其在分度期过程，随着弧面分度凸轮转速的提高，分度盘角速度和接触力都呈现逐步增大的趋势。然而，一方面，随着弧面分度凸轮转速的提高，一个周期内接触力波动次数逐步变少，在一定程度上能够降低弧面分度凸轮与滚子之间碰撞次数，进而降低弧面分度凸轮的工作轮廓曲面的磨损；另一方面，弧面分度凸轮转速的提高将会直接导致角加速度相应地增加，进而导致整个弧面分度凸轮机构的惯性力快速地增大，这对弧面分度凸轮动态特性是不利的。

然而，中国要打造离岸国际商事法庭仍有较多的工作需要开展。其中，如何吸引当事人选择中国法律或者中国国际商事法庭管辖是首要问题。当前，最高人民法院采取的主要措施是安排有丰富审判经验和能够熟练运用中英文的资深法官担任国际商事法庭的法官，并组建国际商事专家委员会。该做法能够增强当事人对中国国际商事法庭的信心，但还远远不够，我们还需要在两个方向上同时努力：一个是国内商事制度的完善，另一个是国际商事法庭规则的设计。

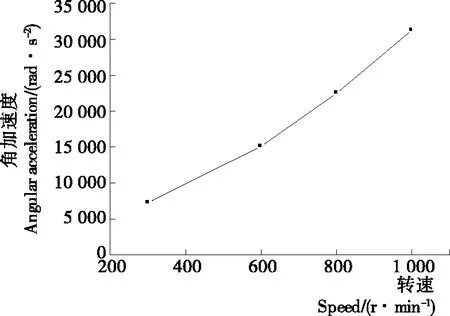
图7 转速与角加速度之间的变化趋势Figure 7 The changing trend between rotational speed and angular acceleration

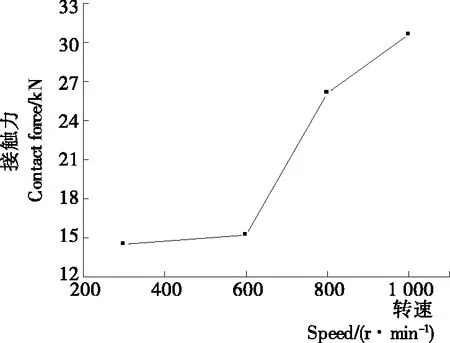
图8 转速与接触力之间的变化趋势Figure 8 The changing trend between speed and contact force

3.2 阻尼系数对弧面分度凸轮机构动态性能的影响

由于弧面分度凸轮始终接触于滚子，而阻尼的大小会对该接触关系产生影响。因此，为了研究不同阻尼对弧面分度凸轮机构动态特性的影响，需要对弧面分度凸轮机构不同的阻尼进行对比与分析，本研究不考虑载荷盘上的负载，设载荷盘的厚度为10 mm，设阻尼系数分别为60，100，150，200 N·s/mm，以此来分析弧面分度凸轮机构的不同阻尼系数对其自身动态性能的影响。

如图9、10所示，随着阻尼系数值的增大，分度盘的最大角加速度值将会先减小再增大，而滚子与分度盘之间的接触力会随着阻尼系数的增大而上升。

随着阻尼系数的增加，其对弧面分度凸轮机构将产生较大的影响。分度过程中，在角加速度值由正转负的中间时刻，凸轮将对滚子产生横越冲击，导致其产生最大角速度值。

在弧面分度凸轮机构一个运动周期内，随着阻尼系数的提高，分度期内接触力波动次数正在逐步减小。在分度期横越冲击时刻，接触力的波动将会随着阻尼系数的增加而相应地增加。因此，横越冲击的波动正比于阻尼系数。在弧面分度凸轮机构中停留期时，由于滚子与凸轮之间基本上无明显的受力情况，所以接触力和角加速度无明显的波动，其数值基本上为零。因此，在停留期，阻尼系数对分度期中弧面分度凸轮机构的接触力影响不大。

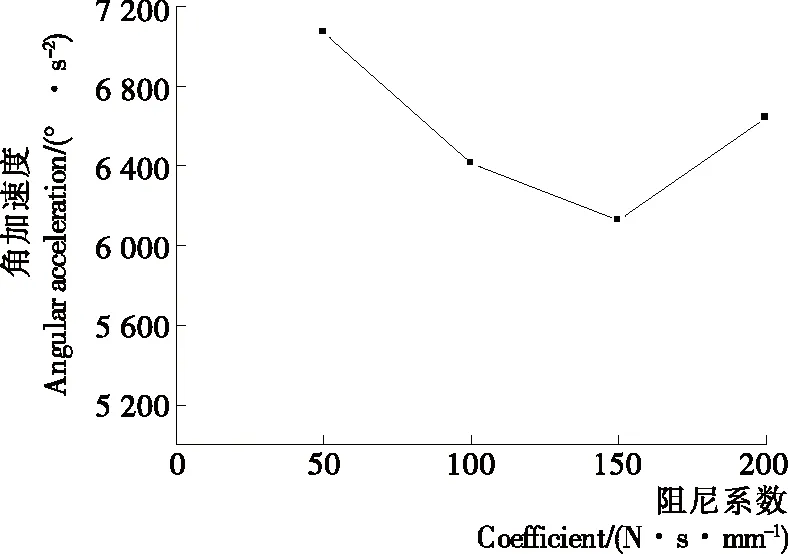
图9 阻尼系数与角加速度之间的变化趋势Figure 9 The trend of variation between damping coefficient and angular acceleration

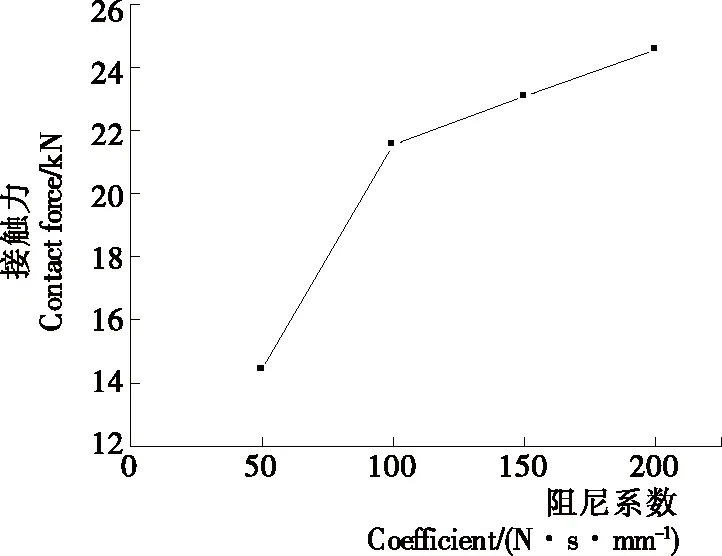
图10 阻尼系数与接触力之间的变化趋势Figure 10 Variation trend between damping coefficient and contact force

4 结论

通过以上分析可知，在整个弧面分度凸轮机构中，需将转速分别对弧面分度凸轮与均匀分布在分度盘上滚子之间接触力和角加速度的影响考虑进去，选取最合理的转速参数，这对提高整个机构的动态特性起到至关重要的作用。而阻尼系数将对整个机构的动态特性产生一定影响，尤其在横越冲击时，角加速度和接触力变化最为明显，弧面分度凸轮与滚子之间的阻尼将在一定程度上防止角加速度方向的改变，这将导致整个机构出现较大的波动现象。因此，在后续的设计中，采用合理的阻尼系数，能够缓解整个机构的明显波动现象，减少其对机构的冲击力，保证其稳定性。