微型胶囊在模拟肠道中的受力模型及流固耦合仿真

李 霄 俞经虎 钱善华 曹 澍

(1. 江南大学机械工程学院，江苏 无锡 214122；2. 江苏省食品先进制造技术与装备重点实验室，江苏 无锡 214122)

微型胶囊机器人作为新型消化道诊疗器械在医疗领域有着广阔的发展前景。体外磁驱动胶囊内窥镜的驱动方式主要包括旋转磁场控制完成的旋进式以及准静态磁场控制的磁导式控制。目前胶囊机器人存在的局部定位不准，姿态控制精度不高等问题为微型胶囊发展的桎梏。谭人嘉等[1]对磁驱动式胶囊内镜与肠道准静态交互的临界滑动阻力建立了Ciarletta超弹阻力模型，研究结果显示内镜外径与肠管内径比(R/r)对滑动阻力影响显著，胶囊头部摩擦力在阻力占比<1%[2]；李传国等[3]提出一种可实现轴向和径向伸缩的仿尺蠖式胶囊机器人，采用直流电机控制钳制油囊实现蠕动，其最大径向输出力达150 g，完整蠕动步距为9.5 mm。张雨等[4]在黏性牛顿流体环境条件下对花瓣型和圆柱形侧壁的旋进式胶囊机器人在管道内进行液体阻力矩分析。张永顺等[5]的4种胶囊结构中圆柱侧壁瓦片表现出较大偏心量es，反映了良好的驱动效果，该模型默认肠道壁为刚性体。迟明路等[6]建立了万向旋转磁矢量的空间磁力矩模型，对磁旋进式花瓣型胶囊内镜的转差角和水平夹角进行改善，提高了非接触驱动性能，对减小胶囊转弯时对肠道的扭曲有显著效果。本研究拟针对椭圆和圆形2种头部外壳形状的磁导式胶囊机器人建立弹性肠道内黏性阻力流体环境下胶囊运动的受力模型；对2种外形的胶囊在不同动力黏度及肠道内径的黏性流体环境下进行多组流固耦合数值模拟，分析磁导式胶囊在弹性肠道壁和黏性流体共同作用下的应力分布以及胶囊对流体和肠道的影响，为磁导式胶囊机器人在黏性液体和弹性肠道环境下磁驱动的外形优化和准确定位提供了理论依据。

1 胶囊体受力分析

胶囊体在肠道环境下运动模型按照胶囊与肠道的相对尺寸可分为2种：胶囊尺寸相对较大的挤压模型和胶囊尺寸较小的流动模型[7]。本研究建立的受力模型主要针对后者。人体肠道液体内环境复杂，认为肠道中运动体受到的动阻力Fd主要分为：流体动压力Fp与流体的黏滞阻力Ff，即

Fd=Fp+Ff。

(1)

1.1 头部流体阻力

设胶囊机器人头部在准静态下与肠道内流体的轴向相对运动速度为νr，设胶囊头部面单元为dS见图1；流体对胶囊头部的轴向力Fp为：

(2)

(3)

式中：

σc(θ)——单元体受流体冲击应力，Pa。

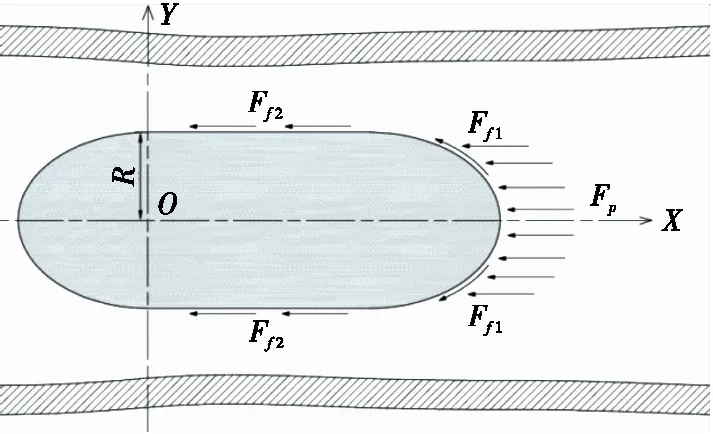
图1 磁导驱动胶囊体在肠道的运动阻力Figure 1 Dynamic resistance of magnetic conductance capsule in intestinal tract

由流体动力学可知：

σc(θ)=ρvr2sin2θ。

(4)

对单元面dS有：

dS=R2sinθdθdφ。

(5)

将式(3)～(5)带入式(2)得到：

(6)

式中：

θ——单元法向(指向球心O)与XOY面的夹角，rad；

R——球面半径，m；

ρ——流体密度，kg/m3；

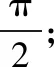
vr——流体相对胶囊体的轴向平均速度，m/s。

1.2 黏滞阻力

肠道液黏度不可忽略[8]，设胶囊头部的黏滞阻力Ff1，圆柱段的阻力为Ff2，胶囊准静态运动时与流体的黏滞阻力Ff有[9]：

Ff=Ff1+Ff2。

(7)

(1) 头部阻力：图2为胶囊头部单元体受力。对于肠道壁头部单元dS，有黏滞相应阻力单元dFf1为：

(8)

式中：

h(θ)——头部单元体距肠道内壁距离为θ的函数。

对于球面体，

h(θ)=H-Rcosθ，

(9)

式中：

H——胶囊轴线到肠道内壁距离，m。

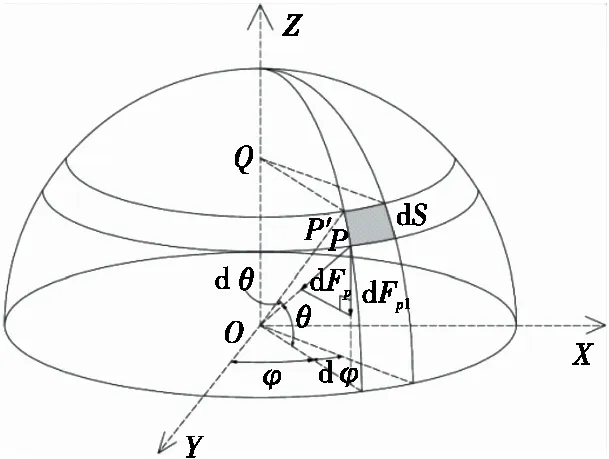
图2 胶囊头部单元体受力Figure 2 Schematic diagram of force element on

参考式(2)有：

(10)

将式(9)代入式(2)并积分得：

(11)

(2) 圆柱段阻力：

(12)

式中：

vr——流体相对胶囊体的轴向平均速度，m/s；

R——胶囊球面半径，m；

l——胶囊长度，m；

H——胶囊壁与肠道壁间距，m；

μ——肠道液动力黏度，Pa·s。

2 数值仿真

人体肠道壁弹性体对肠道液运动起到耦合作用，因此采用COMSOL Multiphysics二维双向流固耦合FSI模块，流场采用k-ε湍流瞬态模型，模型尺寸参数设定为长度200.0 mm，宽度25.7 mm，壁厚2.2 mm。由于人体肠道材料常数曲线显示非线性增长，同等应变条件下，十二指肠的弹性模量较其他肠段显著增大[10]。基于力学性能相近原则采用超弹性Nynon材料，弹性模量8.117 MPa。为了降低两端固定约束造成的应力集中失真现象，设定胶囊始末位置两端距离流体出入口L0为35.0 mm，采用物理场控制网格划分提高网格质量(图3)，以消除出入口边界影响。

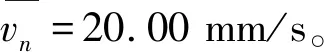
2.1 仿真参数

选取肠道液动力黏度μ，肠道内径尺寸D，2个参数各取2水平进行耦合场仿真，表1给出了各因素水平参数值。

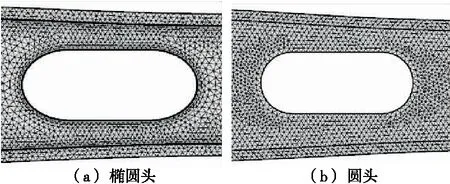
图3 椭圆头和圆头在μ=5.3 mPa·s,D=22.1 mm参数下的模型网格Figure 3 Model grid in μ=5.3 mPa·s,D=22.1 mm oval head circular head

肠道液动力黏度μ/(mPa·s)肠道内径尺寸D/mm胶囊形状5.322.1圆形(C) 20.724.5椭圆形(E)

数值模拟的参数水平数较少，动力黏度参数和肠道尺寸参数仅设置了2个参数水平，没有排布正交试验。按表2列出的各组因素组合匹配模型，将8组制备好的胶囊肠道模型导入comsol，在指定的监测点处插入应力探针进行求解，瞬态求解器采用全耦合自动(Newton)非线性方法，相对容差0.001，恢复阻尼因子为0.75以保证解算效率。

2.2 结果分析

选取了4组内镜尺寸为D=22.1 mm参数水平下的数值仿真结果，应力分布结果和肠道液流速场分布见图4。

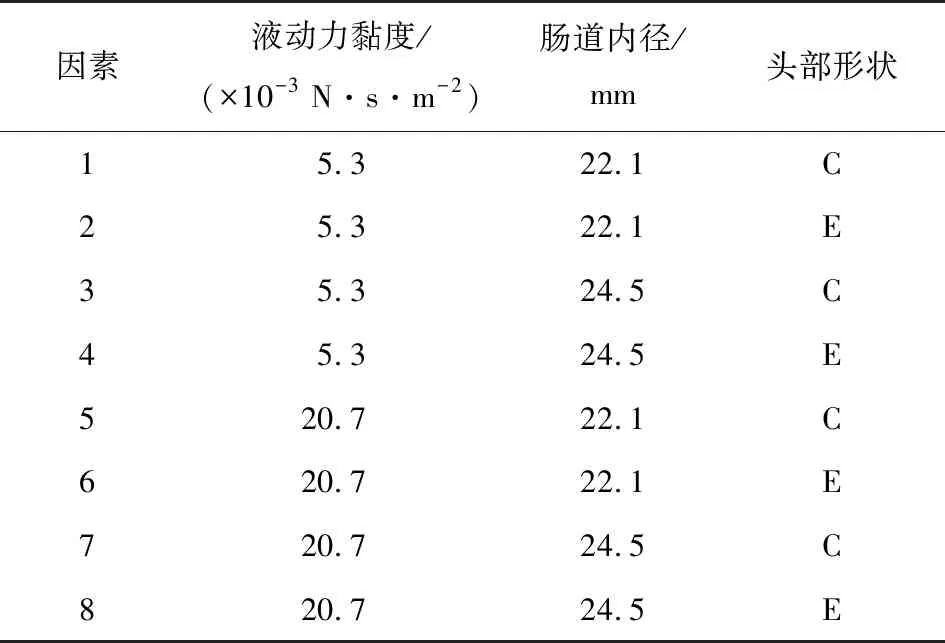
表2 各组因素参数

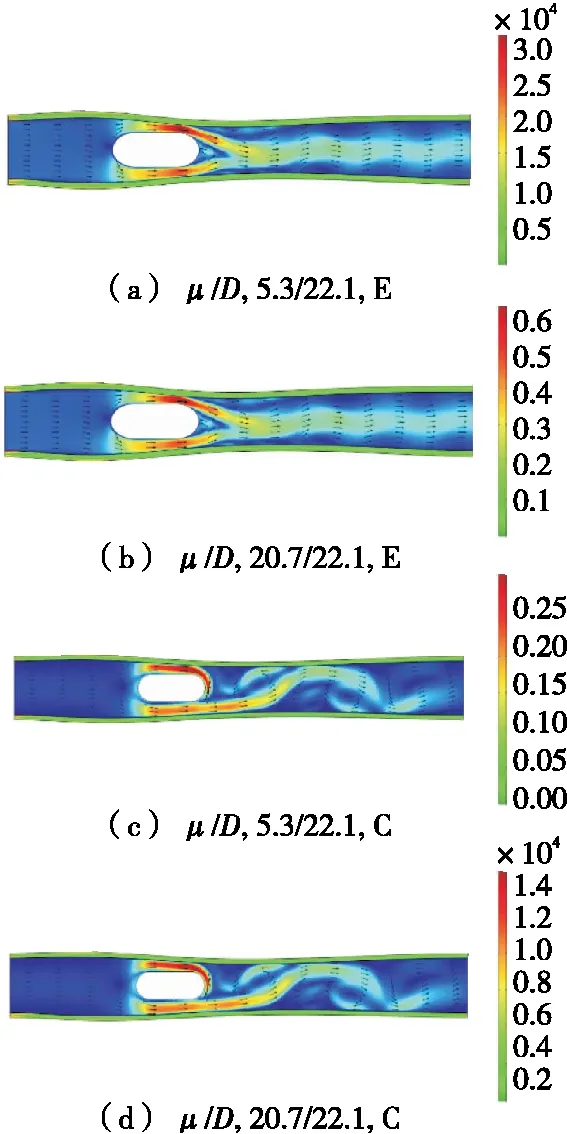
图4 在D=22.1 mm, 3.0 s条件下各组的流速分布

Figure 4 Distribution of flow velocity and distribution of intestinal stress in each group at 3.0 s,D=22.1 mm

图4结果显示：在较低黏度μ=5.3 mPa·s和μ=20.7 mPa·s 条件下，胶囊附近出现局部最大流速，3.0 s时分别为0.315 m/s(椭圆)和0.310 m/s(圆)，模型壁出现最大应力7.75 kPa(椭圆)和9.07 kPa(圆)，主要发生在入口的固定端附近，表明固定端的仍然存在引力集中现象。另外值得注意的是，椭圆外形的第2、6组形成的尾流较为稳定，相比之下圆形胶囊头部的1、5组出现了较为明显的扰流现象。

测取了3 s内各组的指标点应力分布，并按照胶囊形状进行分组见图5。结果显示：黏度较高时胶囊运动应力较大，在动力黏度μ=20.7×10-3Pa·s水平下，系列3、4代表的椭圆形头部3 s内在不同尺寸肠道中受应力均值(19.21 Pa)较系列1、2代表的圆形头部的(21.17 Pa)降低了9.3%；在μ=5.3×10-3Pa·s水平下降低了16.3%。另外取4组(表3)试验组的探点应力点理论值与相应试验值进行了对比。

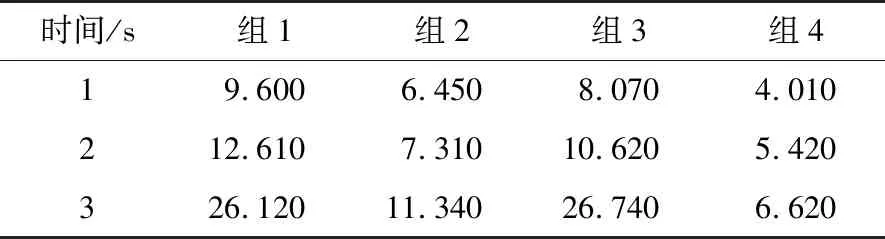
表3 3 s内4组头部α=0°探针处压力理论值

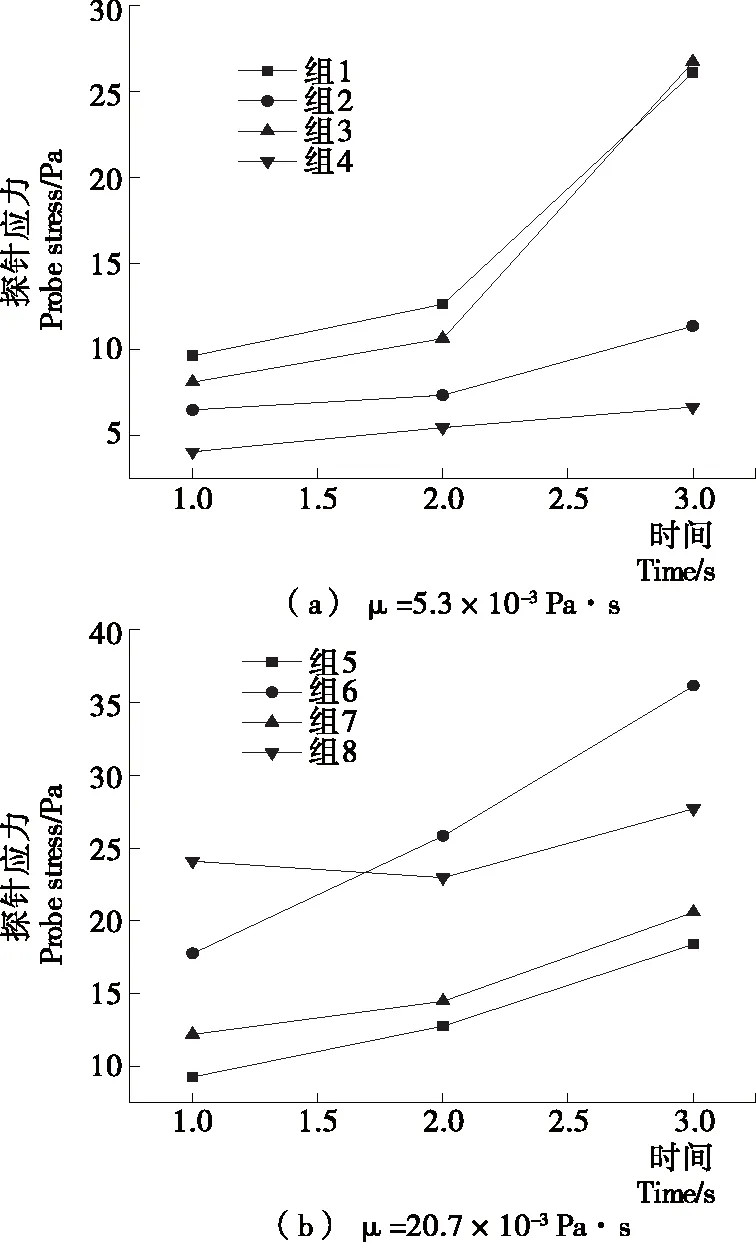
图5 不同动力黏度下胶囊的头部探针测量值Figure 5 Probe value of capsule under different dynamic viscosity

值得注意的是，理论值普遍较试验值略高，可能是理论模型中没有考虑到肠道的弹性扩长，实际运动中的应力值比理论值小。

3 结论

本试验对主动式胶囊机器人在人体肠道内环境黏滞流体中的运动受力模型进行了力学理论分析。采用ComsolMultiphysics模块对胶囊运动进行了不同环境下的流固耦合数值仿真。结果表明：

(1) 两种外形胶囊在不同动力黏度μ与肠内径D下，椭圆形头部胶囊头部监测点所受应力平均值低，肠道壁出现最大应力低，说明在流固耦合环境下椭圆胶囊头部形状有更好的受力分布和肠道舒适性。

(2) 3 s内胶囊在运动黏度高的液体环境中运动时受力变化更平缓，相同胶囊尺寸下，肠道内径越大，胶囊头部受应力越低。胶囊受力计算值比仿真值略低，理论有待进一步研究肠道的扩张因素对耦合状态下胶囊运动的影响。

(3) 胶囊头部形状对低动力黏度流体的流场分布出现扰流作用，两种外形胶囊出现的最大流速相差不大(1.5%)，但流场分布显示椭圆形头部胶囊在低速直线运动时表现出了运动稳定性。