圆都去哪儿了——不同视角下命制“隐圆”

江苏 曾小娟 张朋举

圆是高中数学的主干知识，在高考中占据着重要的地位.纵观近几年的江苏高考试题，可以看出，关于圆的相关问题，无论填空题或解答题，解决的方法都离不开轨迹思想，要有从运动的观点看问题的能力.因此，圆成为试题背景中常常涉及的知识点，并深受各类模考命题专家的青睐，在江苏各大市的高三模考题中屡见不鲜.以下笔者结合近几年江苏各大市高三模考题，谈谈命制试题中隐藏圆的几种不同视角.

一、利用圆的定义

中学数学的教科书中是这样定义圆的：平面内到定点的距离等于定长的轨迹叫做圆.因此，很多命题专家经常围绕圆定义中的“定点”和“定长”这两个关键词不同表征的呈现，将圆的定义隐藏在已知条件里，“万变不离其宗”的来命制试题.

例1.如果圆 (x-a)2+(y-a+2)2=1上恰有两个点到(0，1)的距离为 2，则实数a的取值范围是________.

解决现状：笔者通过批阅自己执教班级学生的解答情况，发现部分学生没能想到圆的定义，将问题转化为两圆的位置关系，而是研究两个方程x2+(y-1)2=4和(x-a)2+(y-a+2)2=1有两组解时实数a的取值范围，使运算变得复杂,虽然最终也能算出来结果，但这种运算显然没能触及问题本质.

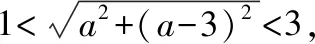
试题命制：已知圆O：x2+y2=1，圆M：(x-a)2+(y-a+4)2=1．若圆M上存在点P，过点P作圆O的两条切线，切点为A，B，使得∠APB=60°，则实数a的取值范围为________．

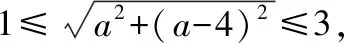
二、利用直角

直径所对的圆周角是直角，这是圆周角很好的一个性质，因此，很多命题专家在命制试题时，在题目中经常隐晦地出现动点和两个定点构成“直角”来隐藏圆.

例2.在平面直角坐标系xOy中，直线l1:kx-y+2=0与直线l2:x+ky-2=0相交于点P，则当实数k变化时，点P到直线x-y-4=0的最大值为________.

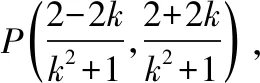
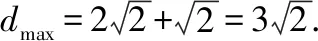
试题命制：在平面直角坐标系xOy中,已知点P(-1，0)，点Q(2，1)，直线l:ax+by+c=0,其中a，b，c成等差数列，点P在直线l上的射影为H，则线段QH的取值范围是________.

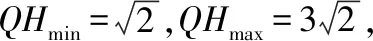
三、利用PA=λPB(λ>0)

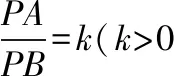
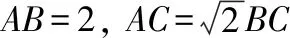
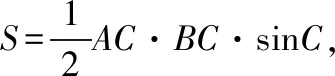
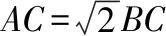
试题命制：在平面直角坐标系xOy中，点A(0,3)，直线l:y=2x-4.设圆C的半径为1，圆心在l上. 若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围.

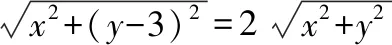
四、利用定长弦的中点

一个定圆内长度一定的弦的中点的轨迹是一个圆，这是大家熟知的结论.因此，很多时候高考命题专家们充分利用这一结论来隐藏圆，命制试题.

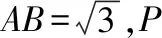
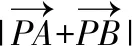
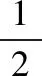
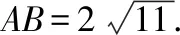
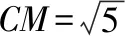
五、利用

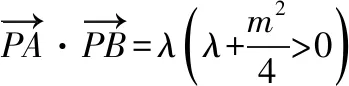
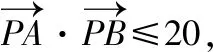
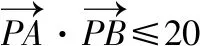
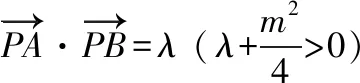
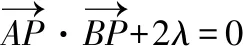
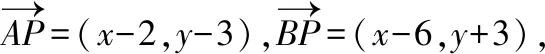
六、利用PA2+PB2=λ(λ>0)

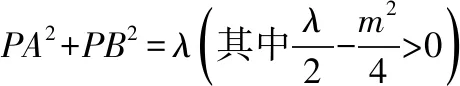
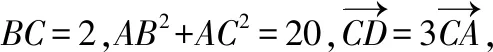
解决现状：大部分同学对上面的“平方圆”结论陌生，且通过建立坐标系，用“坐标”将条件转化为变量间的数量关系的意识淡薄，因此，没能发现动点D的轨迹，导致题目越算越繁，计算出错；当然，也有少数同学通过建系得到了动点D的轨迹方程，然后利用三角换元也得到了正确答案.

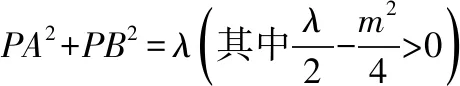
试题命制：在平面直角坐标系xOy中，已知圆C:(x-a)2+(y-a+2)2=1，点A(0,2),若圆C上存在点M，满足MA2+MO2=10,则实数a的取值范围是________.

本题和例6相比，虽然思维容量变小了，但实质不变；只要学生了解“平方圆”，由MA2+MO2=10易得动点M的轨迹方程为圆，进而将问题转化为已知圆C和求出的动点M的轨迹圆有交点的问题，得到a∈[0,3].