从三道高考数学解析几何姊妹题谈新课程理念

广东 王 翠 王 飞

一、问题的提出

一年一度的高考过后，笔者认真研读了2018年高考数学理科的18份试卷，其中有不少新颖别致、富有创意的试题出现，但命题专家在对解析几何部分知识进行考查时，对“解析几何+直线”的命题模式仍是不舍不弃，例如在同年的理科数学试卷解答题中，天津卷第20题、辽宁卷第20题、福建卷第9题、陕西卷第20题、重庆卷第14题、湖北卷第20题、上海卷第23题等都有所体现．尤其是全国卷Ⅰ(理科)的第8题、第11题和第19题第Ⅱ问(2017年也同样出现在理科试题中)、以姊妹题的方式呈现在高考卷中，令人赏心悦目，引起了笔者极大的探究兴趣．这一切说明什么？是命题“偶然”或“必然”，还是源于对新课程理念的凸显？唯有领略考题智慧，才能挖掘深刻的内涵.

1.考题再现

( )

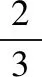
A.5 B.6

C.7 D.8

例2(2017·全国卷Ⅰ理·10)已知F为抛物线C:y2=4x的焦点，过F作两条互相垂直的直线l1,l2，直线l1与C交于A,B两点，直线l2与C交于D,E两点，则|AB|+|DE|的最小值为

( )

A.16 B.14

C.12 D.10

( )

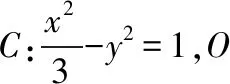
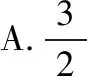
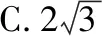
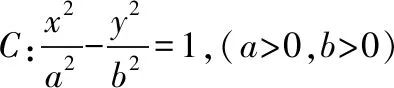
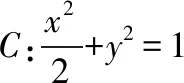
(Ⅰ)当l与x轴垂直时，求直线AM的方程；

(Ⅱ)设O为坐标原点，证明：∠OMA=∠OMB.

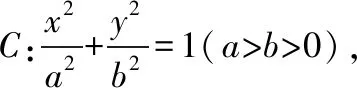
(Ⅰ)求C的方程；

(Ⅱ)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1，证明：l过定点.

2.姊妹题表征的相似性

例1和例2处在选择题的第8题和第10题的位置，难度属中档题，运算量不太大，其表征都涉及“抛物线与直线相交的问题”，而且给出的抛物线都是开口向右的同一条抛物线，只是所涉及的求解目标不同而已.例3和例4两题处在选择题、填空题的中后位置，难度属中档题，两题都涉及双曲线及其渐近线的相关问题，两题的表征都涉及“与双曲线渐近线相交的问题”， 只是所涉及的求解目标不同而已.例5和例6 两题为圆锥曲线的解答题，第Ⅱ问属于压轴题部分，两题的表征都是涉及“椭圆与直线相交的问题”，都需要联立直线方程与椭圆方程，通过消元，利用韦达定理求解化简即可，运用到了“设而不求”的解题思想和命题理念.

从题目所涉及的知识点与题型结构看：姊妹题表征的相似性体现得很完美，让人自然产生探究的兴趣，进而引出了一个可探究的灵动空间．仔细翻阅2018年各地的高考数学试卷中的解析几何题，与上述例题的内容、结构相同的还有全国卷Ⅲ理科的第16题、辽宁卷理科第20题第Ⅱ问等，这些题目的出现是偶然？还是必然？可以肯定地说，它们都是缘于对新课程理念的凸显而设置的高考试题，是命题人在不同地域贯彻新课程理念命题的体现，在编写数学试题时对考查部分数学主干知识、核心概念而采用题型设置上出现偶然“相遇”的相似因素．从这里可以进行探究，从而把握高考命题的思想、理念和核心.

二、解法剖析

通过上述对姊妹题表征相似性的分析，对其解法做进一步的剖析和思考，发现姊妹题的解法也具有相似性．下面只对2018年三道题的解题思路和方法进行深层次的剖析.

1.例1的几种解法

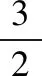
与y2=4x联立得y2-6y+8=0，解得yM=2,yN=4.

进而可得点M(1,2),N(4,4).

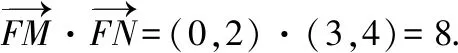
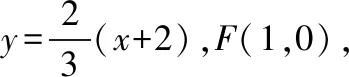
设M(x1,y1),N(x2,y2)，

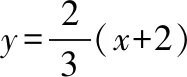
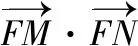
=(x1-1)(x2-1)+y1y2

=4-5+1+8

=8.

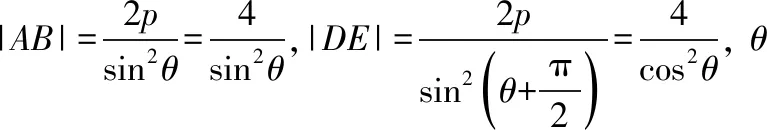
例1和例2的解题思路和解题方法基本一样，只是题目的表征有一点差异，可以说不同的题目用相同的解法去解决，再加上题目的结构特征如抛物线的方程一样，又有相同位置的焦点(右焦点)和截抛物线的直线，一个目标是求向量的数量积，另一个目标是焦点弦长的和的最小值．这两题在2017年、2018年连续两年出现，即使是“偶然”，也有“寓意”，更加凸显了新课程理念是编写高考数学试题的基本思想，其内涵丰富，进一步确定了直线与圆锥曲线的关系是高中数学的重要内容和高考的核心，也给数学教学带来了很大的启发.

2.例3的解法

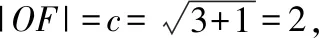
则∠MOx=∠NOx=30°，不妨设OM⊥MN,

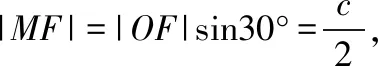
且|FN|=|OF|=c.

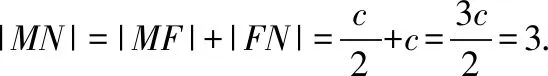
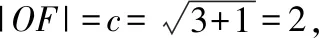
则∠MOx=∠NOx=30°，不妨设OM⊥MN,

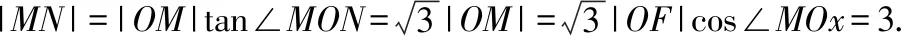
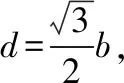
例3和例4的几种解题思路、解法也具有相似性，它们都是围绕双曲线及其渐近线的几何性质进行解题，难度不大，方法多样，既体现了高考命题的思想，又考查了考生对主干知识和核心概念的理解与应用，两题的结构差不多，都需要去挖掘题目所给的已知条件，利用特殊三角形的性质进行求解，两题实属同一类型的试题，差异在于题目的所求目标不同.在2017年、2018年连续两年出现，实属“偶然”，并非“必然”，只要细细揣摩，定是专家命题时为了“有意”凸显新课程理念，所选的载体相似而无意造成的“有意”.其目的只有一个，就是让高考数学试题凸显新课程理念，并在高考复习中起到导向作用，构建了以直线为桥梁来解决有关问题的新模式，给数学教学带来新的启发.

3.例5的解法(主要针对第Ⅱ问)

解法一：当直线l与x轴重合时，∠OMA=∠OMB=0°;

当直线l与x轴垂直时，OM为线段AB的垂直平分线，则∠OMA=∠OMB；

当直线l与x轴不重合也不垂直时，设直线l的方程为y=k(x-1)(k≠0)，点A(x1,y1),B(x2,y2)，

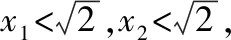
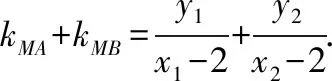
由y1=kx1-k,y2=kx2-k，

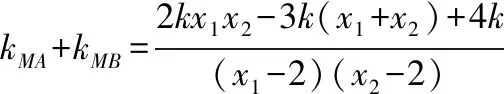
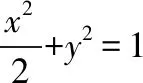
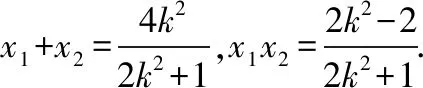
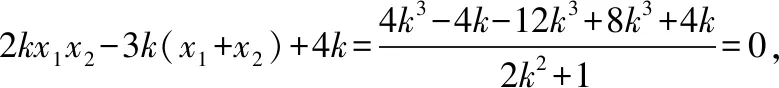
从而kMA+kMB=0 ，故MA,MB的倾斜角互补，所以∠OMA=∠OMB.

综上，∠OMA=∠OMB.

解法二:换一种直线方程的设法.

①当直线l平行于x轴，即l：y=0时，A,B为长轴的端点，显然有∠OMA=∠OMB=0°.

②当直线l不平行于x轴时，可设l：x=my+1，与椭圆方程联立后并整理得(m2+2)y2+2my-1=0,

设点A(x1,y1),B(x2,y2)，

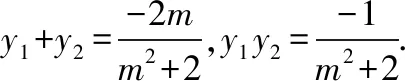
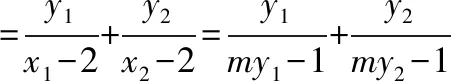
=0,

这也就意味着直线MA,MB的倾斜角互补，所以∠OMA=∠OMB.

综上，∠OMA=∠OMB.

【评析】例5的解法一和解法二具有相似的地方，即坐标法；也有不同的地方，即直线方程的选取不同.总的解题思路就是通过联立直线方程与椭圆方程，通过韦达定理进行化简求解，都运用到了“设而不求”的解题思想，运算量不算大.而例6的第Ⅱ问，同样是利用韦达定理以及“设而不求”的解题思想.两道题都涉及两条直线的斜率之和的求解，都需要考生具备一定的运算能力，意在培养考生解题能力和运算能力.这两题在2017年、2018年连续两年出现，并非“偶然”.此外，从两题的位置来看，2017年处在第20题的位置，而2018年处在第19题的位置；从试题的难易程度上讲，2018年的第Ⅰ问和第Ⅱ问，明显比2017年的两问要简单很多，而且运算量也相对小一些.这是否意味着今后高考解析几何的解答题会降低难度呢？认真揣摩，定是命题专家为了“有意”凸显新课程理念，而巧设的命题导向.

三、探究命题思想，揣摩考题核心

1.姊妹题“巧合”点

主要从知识点的表征和数学试题的结构特点进行分析.

例1和例2两题都是围绕一条曲线，即抛物线进行设计.给出的抛物线都是开口向右的，所给直线具有“过定点”的特殊性，表明了与x轴交点的坐标，涉及抛物线与直线的位置关系，即相交．例1(2018年)涉及焦半径所在向量的数量积问题，例2(2017年)涉及焦点弦长问题，其实质都是直线与抛物线相交而引发的相关问题.

例3和例4两题都是围绕双曲线及其渐近线设计的试题，主要考查双曲线及其渐近线的几何性质，例3和例4所给试题的结构、形式及考查的实质是一样的，都要挖掘题目所给的条件，得出一个特殊三角形后再求解，解题方法几乎是一样的，只是所求目标和数据不同而已.

例5和例6两题都是围绕椭圆设计的试题，主要考查椭圆与直线相交的问题以及考生的解题能力和运算能力，都采用了韦达定理和“设而不求”的解题思想，体现了历年来全国高考数学“亘古不变”的命题导向以及新课程理念.

2.命题人“有意”凸显新课程理念

命题人凸显新课程理念是“有意”的：主要体现在命题人对数学试题的设计思想、理念．命题人为了凸显数学主干知识、核心概念，以及能力立意等方面，渗透了对数学知识点和数学思想方法的考查，数学能力及综合素质的考查等几个方面.

(1)命题思想的“凸显”

例1在考查知识点上的特点，包含了高中数学所要重点考查的解析几何中圆锥曲线的定义，性质，直线与其位置关系.这说明了命题人的命题思想是“注重大家关注的高考重点，同时凸显对解析几何与直线的综合是高考的热点问题”.体现这一命题思想在同年的数学卷(理科)中有：天津卷第20题、辽宁卷第20题、福建卷第9题、陕西卷第20题、重庆卷第14题、湖北卷第20题、上海卷第23题等．可见在高中数学教学中的重要性，从而才有命题人“冒险”出此“奇招”进行命题，可谓匠心独具.

(2)设计思想的“凸显”

2018年的三题(例1和例3和例5)是理科题，与2017年的三题(例2和例4和例6)是“同类同型”的姊妹题，这就足以说明命题者重点强调这三道题所含的解析几何的基本思想，目的是体现对解析几何的基本特点和性质的考查，同时加强对数学思想方法的考查，突出能力与素质导向的考查，深化能力立意，表现在思维容量较大，运算量较小，几乎不涉及技巧，仅是对解析几何的基本方法(即坐标法)和几何意义的理解与应用的考查.这三道题是对圆锥曲线与直线位置关系的考查，又在直线与解析几何知识网络的交汇处设计试题，拓宽了解析几何命题的思路，再加上连续两年出现，更加“凸显”了命题专家的设计思想.

(3)知识点的“凸显”

通过上述设计思想的“凸显”分析，大家已经明白，例1、例2、例3、例4、例5和例6的命题方式，即知识点(直线、双曲线、椭圆、抛物线)的选取、相关量(向量等式、数量等式、个别数据等)的表示方式、位置关系(直线与曲线的位置、直线与x轴交点)的形式体现等等，给解题者的感觉是命题时“有意”进行了合理的、恰当的编排，即2018年的三题例1和例3和例5与2017年的三题例2和例4和例6是“同类同型”的姊妹题.这样进行数学命题，“凸显”了数学命题是从数学整体意义上设计试题，强化数学的主干知识和核心概念，重点关注解析几何中的直线与圆锥曲线位置关系在高中数学和高考中的重要地位，即重视对数学各知识点的整体性和综合性的考查.

(4)解题思路的“凸显”

从对例1和例2的解法点评中可以看出，两题的几种思路、对应的解法既有差异又很接近，但都是以坐标法为主，同时依据抛物线几何意义给解题带来的方便，很快地解决问题．例3和例4两题的解法点评中可以看出，两题的解题思路、对应的解法几乎一样，都运用到了特殊三角形的性质进行解题.例5和例6两题的第二问的解法点评中也可以看出，两题的解题思路、解法步骤几乎一样，都运用到了韦达定理和“设而不求”的解题思想.只不过在直线方程的选取上，设法不同，运算量也会有所不同，但是总的解题思路是不变的.

总之，2018年与2017年的三对姊妹题在解法上有着极其相同的解题思路和解题方法，2018年的其他省市的高考题中也有此类题，这就“凸显”了淡化特殊技巧，强调对数学思想方法的考查.这一点是高考命题专家共同认可的，在高考题中体现得非常明显.

3.透过姊妹题“偶然”呈现，揣摩高考命题的核心

仔细分析上述各题，发现这些题考查数学基础知识，数学思想的合理运用、解题的策略以及运算能力，还有数学知识的迁移能力等几个方面．从中进一步还会读出高考命题的核心，主要有以下几点：重视数学思维能力的考查力度，表现在对“解题策略”的注重；突出数学思想方法，表现在对“通性通法”的注重；突出计算能力的考查力度，表现在对“数学式子的化简”的注重.如例1、例2、例5、例6的几种解法中对计算能力的考查很明显，例3、例4的几种解法表明突出几何意义，题目的难度也会降低，突出了数学思想和数学方法及运算能力的考查，从而体现了命题人主干知识重点考的命题理念.作为数学教师，应该探索高考数学题“考什么”和“揭示了什么”，进一步揣摩“高考的核心”，这是探究问题应具有的态度，从而会进入“悟”其必然，“品”其数学味的意境.

四、深究新课程理念的“凸显”，思考2019年的命题变化

从上述的分析可知，解析几何与直线的综合仍是高考的热点问题，尤其用几何性质解决解析几何问题更能体现新课程的理念.2018年数学卷在这方面的命题方式不仅体现了数学的本质，突出了选拔功能，为实施课程改革的省份和2019年刚实施课程改革的省份提供了导航方向和对接的平稳过渡.因此，2019年的全国卷解析几何部分的命题不会有大的变化，依然是“解析几何+直线”的综合考查模式，仍是高考数学的热点问题，在命题形式上仍有所体现，但力度不会大，试题难度会稍微有所下降.