巧妙处理力学中的无穷网络

周启勇

(深圳中学，广东 深圳 518000)

物理竞赛中无穷网络更多的是在电路中应用,特别是无穷网络等效电阻的计算.求解此类问题的基本思路与技巧,就是要深刻地理解“无穷”的含义,弄清楚“无限”与“有限”这对矛盾,巧妙地创设条件,使无限向有限转化.

如图1所示的电路为开端型半无穷梯形网络,由于它是半无穷网络,所以a、b间的等效电阻与去掉一个格子后的电阻是相等的,即

图1

力学中也有类似的问题,我们通过以下例题讲解力学中的无穷网络的巧妙处理.

图2

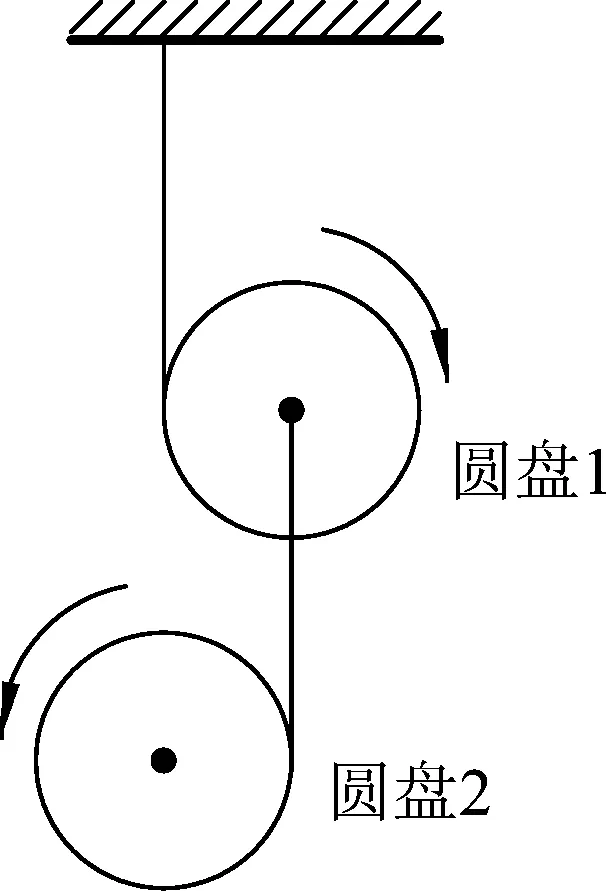
图3

图4

解析:如果只有少数几个,比如3个圆盘串联,我们常用牛顿运动定律和转动定律求解,如图4,由牛顿第二定律

mg+T2-T1=ma1,

mg+T3-T2=ma2,

mg-T3=ma3.

通过圆盘轴心的转动,应用转动定律

角加速度和线加速度的关系为

由以上3式可得

4a1-a2=2g,

-a1+4a2-a3=2g,

-a2+3a3=2g.

解之得到

但对无限多个圆盘,我们无法列无数个方程并求解,那我们如何处理呢?我们可设系统包含N个串联圆盘,再去找通用方程,具体解法如下.

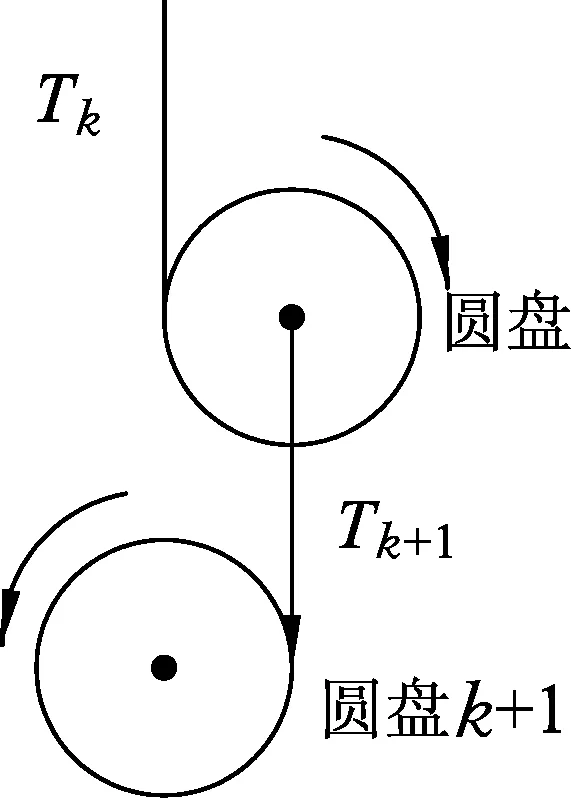
图5

设系统包含N个串联圆盘,如图5所示,从上向下对圆盘编上号码.第k号圆盘受到第k根线向上拉力Tk、向下重力mg以及第(k+1)线向下拉力Tk+1.列出第k个圆盘动力学方程

mg+Tk+1-Tk=mak，

(1)

式中ak为圆盘质心加速度在运动方向上加速度分量,对于任何圆盘都适用.因为第(N+1)号线根本就不存在,所以TN+1=0.由此可见,对于k=1～N,我们列出N个方程式,这N个方程中含有2N个未知量(ak,Tk).

而对第k个圆盘又有

ak=Rβk+ak-1,

k=1～N.

从这方程式中取k和k+1表示拉力方程,代入(1)方程式,最后得到

-ak-1+4ak-ak+1=2g(k=1～N).

(2)

在这方程组中应该认为a0=0,因为这是第一个圆盘悬挂点的加速度.没有第(N+1)根线,TN+1=0,所以aN+1=aN.

我们根据(2)式以展开形式,列出对于3个圆盘情况下的方程组

4a1-a2=2g,

-a1+4a2-a3=2g,

-a2+3a3=2g.

(3)

此方程组与前面分开列是一样的,解之得到

注意,在N为任意有限值的情况下,方程式(2)均可以解答,其实它对于即使N→∞情况也是正确的.

假设第一个圆盘的加速度等于

a1=cg，

(4)

式中c是某一常数,现在过渡到以加速度a1运动的坐标系中,在此加速坐标系里描述所有圆盘的运动.从第2个圆盘开始,这与原来的问题相似,类似无穷网络的等效电阻,区别只是在等效重力加速度为g′的引力场中进行运动

g′=g-a1=g(1-c).

若去掉第1个圆盘,因为N→∞,圆盘依然是无穷多,自然认为上边(第2个)圆盘的加速度等于a′=cg′.

因而,在静止参考系里第2个圆盘的加速度等于

a2=a′+a1=cg′+cg=c(g′+g)=

cg(2-c).

(5)

将表示a1和a2的(4)和(5)式代入方程组(3)第一个方程中,并求出c.

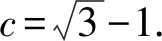
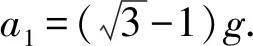
我们可分析出在不同情况下,第1个圆盘的加速度分别是

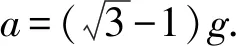
图6

例2.如图6,有质量的圆柱体(质量为M)和无质量的平板组成的无限结构,柱板之间无滑动即纯滚动,整体放在水平桌面上,现给最下面的底板—水平加速度a.试求最底端圆柱加速度.

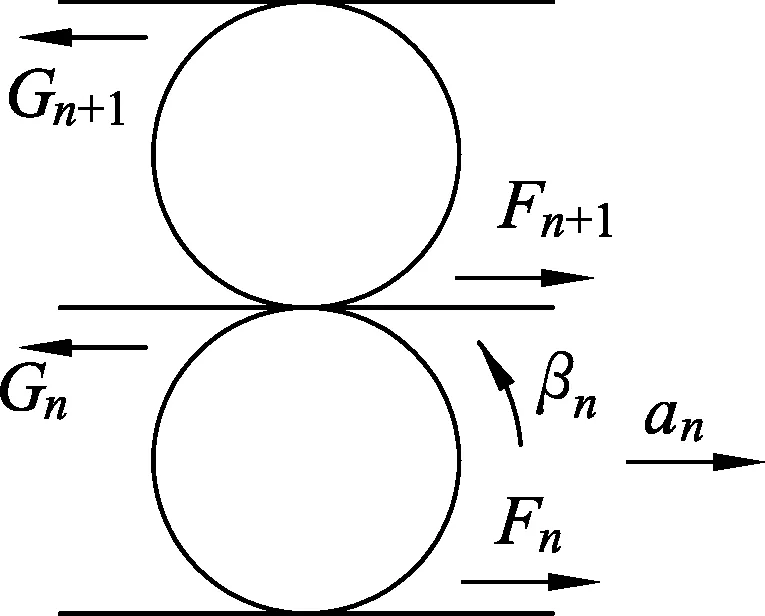
图7

解析:同一行中的两个圆柱体以相同的方式移动,因此我们可以简单地将它们视为具有质量m=2M的一个圆柱体.如图7,标记板施加在圆柱体上的力.其中,F是来自圆柱体下方平板的力,G是来自其上方木板水平方向的力.

由牛顿第二定律,因为板是无质量的,从而有

Fn+1=Gn.

我们的 (求解) 策略是根据其下方圆柱体的加速度,来求解每个圆柱体的质心加速度和角加速度.由于要求解两个量,我们需要获得两个与加速度相关的方程.一个方程来自F=ma,τ=Iβ和牛顿第三定律的组合,另一个方程由纯滚条件给出.

根据图7中,给出的a的方向为正方向,第n个圆柱体的牛顿第二定律和转动定律分别得

Fn-Gn=man.

(1)

(2)

求解这两个关于Fn、Gn的方程得(3)，(4).

(3)

(4)

而我们有Fn+1=Gn,从而可得(5)式.

(5)

利用圆柱体相对板无滑动的条件,第n个圆柱体上方板的加速度用圆柱体的加速度和角加速度表示为an-Rβn,但这块板也可以看成是第n+1个圆柱体下方的板,于是

an+1+Rβn+1=an-Rβn.

(6)

(5)、(6)式为an+1、βn+1关于an、βn的两个方程,可以化为(7) 式,

an+1=-3an+2Rβn,

Rβn+1=4an-3Rβn.

(7)

又有an+2=-3an+1+2Rβn+1.

消去Rβn+1和Rβn得

化简得

an+2+6an+1+an=0.

(8)

因为这个系统是线性的,即第1个圆柱的加速度正比于最底下板子的加速度.设比例系数为c,即a1=ca.由于这是一个无穷网络,如果遮掉第1个圆柱和底板不看,把第一个圆柱上方的板视为底板,则这块“底板”的上方也是一个一模一样的无穷系统,与之前的系统有相同的性质.所以,这块“底板”上方的圆柱的加速度a2和“底板”的加速度a′,也有相同的比例系数c,即a2=ca′.重复这个分析过程可知,所有圆柱的加速度,和其下方板加速度的比例系数都为c.另一方面,板子的加速度之间也是成正比的(因为这个系统是线性的).所以圆柱的加速度之间也是成正比的,比例系数设为λ,即a2=λa1,a3=λa2,a4=λa3……

又由(8)式,得

(λ2+6λ+1)an=0.

(9)

注意到 |λ2|>1,则当n趋于∞时,λn会趋于∞.这不符合能量守恒,应舍去.

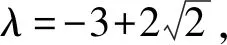
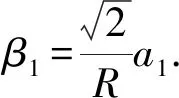
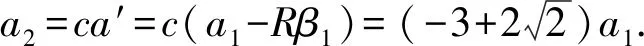
注:无穷网络因为无穷,无法每一个对象都列方程求解,但我们可以找到类似的关系,使无穷变与有限.常用的方法有极限法、递推法、类比法等方法求解.