退役锂动力电池SOC预测建模与分析

张燕习，刘 雪，张 贺，张持健*

(1.安徽瑞赛克再生资源技术股份有限公司，安徽 芜湖 241007；2.安徽师范大学 物理与电子信息学院，安徽 芜湖 241002)

0 引言

新能源汽车技术的发展不断完善，但汽车动力电池寿命只有短短几年，相应的是大量锂电池的回收与梯次利用问题。当动力电池 SOC降低到新电池 SOC的70%～80%时便无法满足车载使用要求，而退役后的动力电池组可依据其真实 SOC仍然可梯次用于小型电力储能设备、低速电动车及照明系统等对电池性能要求较低的领域。

目前，经典的SOC预测方法各有长处，但研究对象大部分是针对全新锂电池，没有考虑到退役电池的物理化学特性。随着充放电循环次数增加，锂电池极化内阻和欧姆内阻作用混合到一起，不能区分，与新电池能力有巨大差异。必须对退役电池的SOC预测用其他方法探究。退役电池放电过程开始的一段时间，欧姆龙内阻和极化内阻使退役电池产生瞬间压降和压升，这段时间的数据给SOC预测带来较严重的误差[1]。

文献[2-3]用传统的BP、RBF神经网络预测电池放电中非线性变化下的SOC值，RBF神经网络法计算速度比BP神经网络更快，效果相当(平均误差在5%以内)；文献[4]中提出利用粒子群优化最小二乘向量机参数的建模方法提高了预测的精度(在0.66%～2.42%范围内)，计算较为复杂。考虑到退役动力电池的特殊非线性关系对SOC的影响，本文采用优化的粒子群算法结合改进的RBF神经网络算法对退役电池SOC进行动态预测，采集大量实验数据结合MATLAB中编写的优化算法做仿真实验，结果表明使用该方法预测退役电池SOC误差稳定在1%以下，提高了退役电池SOC的预测精度，加快了运算速度，验证了该预测模型的可行性。

1 RBF神经网络模型

RBF神经网络是一种前向型神经网络，具有3层结构：输入层、隐含层和输出层。与BP神经网络不同，RBF神经网络隐含层由径向基函数(通常是高斯函数)组成，没有与输入层的权重连接，输入向量直接映射到隐层。径向基函数的中心点确定输入与隐层之间的映射关系[5]。隐含层到输出层是线性映射，输出为隐含层的线性加权。具有m个输入、n个隐含节点和1个输出的RBF神经网络如图1所示。(x1,x2,...,xm)是输入层，在预测SOC时的输入为退役锂动力电池的端电压与负载电流；(φ1,φ2,...,φn)是隐含层，径向基函数φn以cn为中心，构成隐含层中的隐含节点；y是输出层，输出结果是电池的SOC。(w1,w2,...,wp)是隐层与输出层的权重。

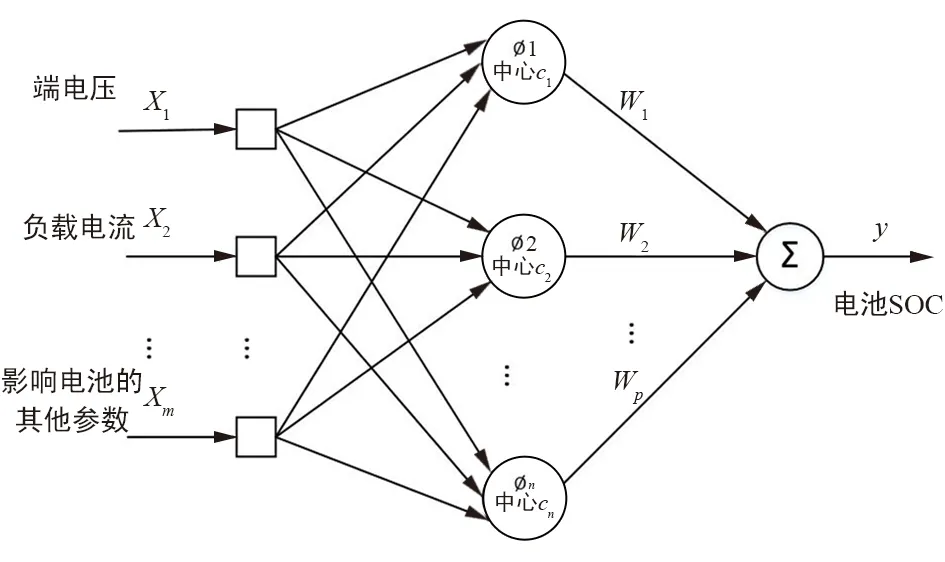
图1 RBF神经网络结构

RBF神经网络有如下非线性映射：

(1)

(2)

式中，δi为基函数围绕中心点的宽度，ci为第i个基函数的中心值，Qi(x)为第i个隐含节点的输出值,wij为第i个基函数与yj之间的连接权重，j为输出节点的数量。

图1中单输出的RBF神经网络里，j=1，即

(3)

在用RBF神经网络做SOC预测时，需要学习基函数的中心值、扩展常数和权值[6]。

2 粒子群算法优化RBF神经网络

2.1 粒子群算法原理

PSO是群体进化算法之一。在PSO中，优化问题的解决方案是搜索空间中的粒子，所有粒子都具有由优化函数控制的适应度[7]。每个粒子都有一个确定方向和距离的矢量速度，粒子跟随当前空间中的最佳粒子搜索。粒子在最好位置所得到的目标函数的值被称为个体极值(pbest)，在所有粒子的个体极值中最大或是最小的那个值是全局极值(gbest)[8]，对应的就是全局最优粒子的位置。粒子在一次次迭代中通过跟踪pbest和gbest来更新自身。粒子群优化RBF的模型步骤如图2所示。

图2 PSO-BF算法工作流程

粒子通过如下2个公式不断更新其速度Vi和位置Pi：

(4)

(5)

式中，c1，c2为学习因子，r1，r2为区间[0,1]上的随机数，w为权值，t为迭代次数。

粒子群算法很容易陷入局部极值并形成早熟，使优化后的RBF神经网络预测退役锂动力电池SOC误差离散度较大。

2.2 量子粒子群优化RBF神经网络

粒子群优化算法不是全局收敛算法,对于离散和拐点较多的映射关系优化问题处理不佳，容易陷入局部最优。而在量子空间里，粒子是聚集态，在搜索空间的任意一点可以一定概率密度存在，因此可以搜索整个解空间[9-11]。

在量子粒子群算法(QPSO)中，运用Monte Carlo法：

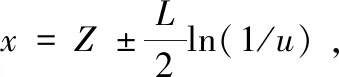
(6)

引入pbest的平均值:

(7)

其中，M为粒子的总数,pbesti为第i个粒子的当前最佳位置。

进化方程为：

x=Z±a·|mbest-x|·ln(1/u)，

(8)

式中，Z为局部吸引点；α为收缩-膨胀因子，是控制粒子收敛的参数[12]。

2.3 QPSO-RBF神经网络预测模型的建立

使用QPSO对RBF网络的权值、阈值优化，建立映射关系，构建QPSO-RBF神经网络模型。

量子粒子群优化RBF的模型步骤如下：

① 对训练集、测试集数据归一化；

② 计算聚类中心数目CN；

③ 初始化种群，维数D=CN+1，种群大小S=20，最大迭代次数Tmax=100，学习因子c1=c2=2，设置惯性权重范围是[0.4,0.9]，阈值范围为[-2,2]，随机生成粒子初始位置；

④ 计算适应值，找到当前个体最优Pgbest和全局最优Pgbest；

⑤ 每次迭代时惯性权重递减，计算扩张因子，更新粒子位置，重新计算适应值；

⑥ 达到最大迭代次数或者全局最优位置时，算法终止，确定粒子的最优适应值和全局最优位置；

⑦ 提取最优粒子；

⑧ 对测试集的输出反归一化，得到结果。

3 实验仪器与样本选取

本文采用的动力电池为电动汽车拆下的退役锂电池包，包含80节18 650单体锂电池。其额定容量为1 800～2 600 mAh，充电限制电压为4.2 V[13]。本实验使用了BTS 7.6x电池检测系统，具有电池组中单个电池电压和温度的测量、恒功率(电压)充放电等功能，可设置SIM工步，满足单体电池在国标下的充放电功能，并同时获取大量网络训练所需样本。本实验将电池包拆分为10组，每组8节单体锂电池进行测试。

根据下位机设计的数据采集电路，退役电池以不同的倍率(0.1C,0.2C,1C,2C)放电。Matlab程序随机选择实验收集数据作为QPSO-RBF网络的训练样本，另一部分作为测试样本[14-15]。选择2组16节单体锂电池4个放大倍数的典型样板数据作为预测模型的输入，SOC为网络的输出，图3为实验中BTS 7.6x检测系统同时为两组电池放电测试的联机情况。

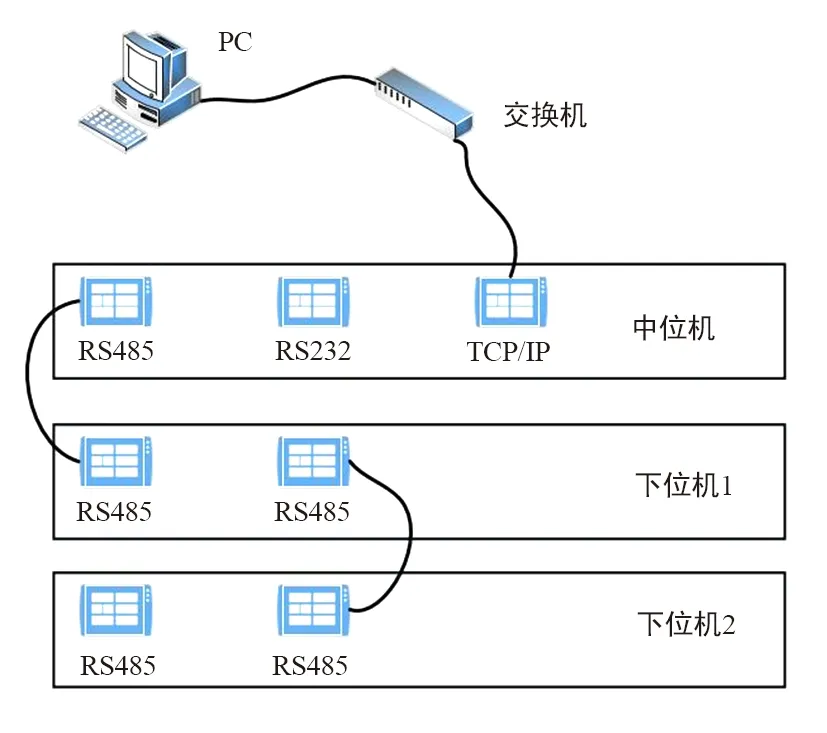
图3 电池组在线联机检测

4 算法仿真及对比分析

在Matlab中借助RBF工具箱，同时利用搭建好的PSO-RBF、QPSO-RBF模型，将电池数据以Excel表格形式导入进行不断地训练与学习，目标误差设为0.001，种群大小为20，迭代次数为100，隐层神经元数量与样本数量相同。径向基函数的扩展系数sc越大，输出结果越光滑，但太大的sc值会增大函数逼近误差与计算复杂度[16]。经调试，sc=0.8时，训练速度更快，误差变化率相对较小。训练结果如图4和图5所示。

图4 3种模型训练误差对比

从仿真结果来看，在旧电池SOC预测方法中，PSO-RBF模型比RBF直接预测更接近实际值，QPSO-RBF模型的精确度更高(如表1所示)。RBF网络模型的误差离散度大，集中在10%以下。PSO-RBF网络模型误差大部分不超过3%。QPSO-RBF网络模型较稳定，均不超过1%。在15次迭代之后，QPSO算法收敛得更快并且具有比PSO算法更小的适应度。说明QPSO-RBF模型降低了计算复杂度，更容易得到最优解。

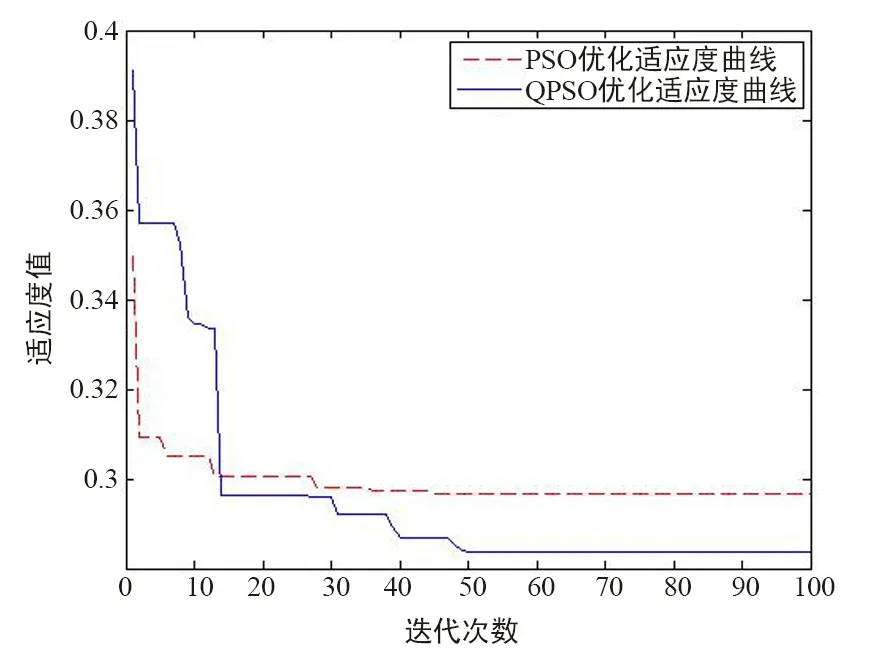
图5 优化适应度曲线

表1 几种模型预测电池SOC情况

模型测试对象平均误差误差离散度BP[2]全新锂电池≤5%较小RBF[3]全新锂电池≤5%较小PSO-SVM[4]全新锂电池≤2.5%小RBF退役锂电池≤10%大PSO-RBF退役锂电池≤3%较小QPSO-RBF退役锂电池≤1%小

5 结束语

新能源技术的迅速发展，使得退役锂动力电池SOC的准确预测对于其梯次应用有重要意义。本文通过对几种常见的预测锂动力电池SOC神经网络模型进行实验分析，提出了改进的QPSO-RBF动态预测模型，克服了现有模型精度不高、误差离散度较大的不足。理论分析和实验结果表明，该方法不仅相对于其他模型适应度较好、收敛速度更快，且预测的退役锂动力电池SOC值与实际值的相对误差小于1%，具有较高的稳定性。本文为退役锂动力电池SOC预测提供了一种适用的新模型，具有广阔的应用前景。