大型水电站整体时空经济运行模型及其算法

张 竞

（青岛世鸿达装饰工程有限公司，山东 青岛 266000）

随着我国经济的不断发展，水电站也需求进行相应的升级与改造。现今，针对大型水电站的经济运行很多学者提出了优化的方法，传统的方法包括动态规划法、拉格朗日松弛法、分支界定法、优先顺序法等等，但是这些传统方法都存在着一定的缺陷，例如动态规划法的运算时间过长，无法在合理的时间内求出满足要求的解；拉格朗日松弛法无法处理模型中多种约束条件的耦合；分支界定法运算过程复杂，同时运算的时间较慢，准确度非常低；优先顺序法是在机组满负荷耗水量的基础下进行排序的，这种情况与实际情况偏差较大。本文主要对大型水电站整体时空经济运行模型及其算法进行研究[1]。

1 大型水电站整体时空经济运行模型构建

该模型主要采用以电定水准则，在用电日负荷量固定的前提下，满足所有的约束条件，对水电站的经济运行进行合理的规划，是水电站的总用水量达到最小，目标函数表示为：

式中：minP 表示的是水电站在运行时间内总耗水量，包括机组开、停机以及发电过程所产生的耗水量；T 表示的是水电站运行的时间；S 表示的是水电站运行的空间；Qi表示的是第i 台机组的耗水量；表示的是在时段t 内机组i 的状态，主要分为两种状态：开机和关机，分为用1 和0 来表示。

本模型的约束条件主要分为旋转备用约束、机组出力约束、负荷平衡约束、最小开停机时间约束，其表达式如下：

1.1 机组组合优化

根据上述给定的目标函数与约束条件，对机组组合进行优化，主要采用的是扩展蚁群算法，其是对传统蚁群算法的改进[2]。

扩展蚁群算法在传统蚁群算法的基础上，将蚁群数量进行了扩展，用M 表示，而每个蚁群有N 只蚂蚁，与水电站中的机组数量对应，1 和0 表示的是机组的开、关机状态。在扩展蚁群算法的每条路径上包含蚂蚁信息素，在算法的初始状态下，每条路径包含的信息素相同，在水电站运行时段，每个蚁群内的蚂蚁会从不同起点在信息素的引导下构建蚂蚁路径，直到水电站运行时段结束，形成N 条蚂蚁路径[3]。这些路径共同组成了水电站中机组的组合方式。制定稳定最优表进行经济符合分配，计算总耗水量，找出M 个蚁群中的最优解，输出相应的结果。

1.2 经济负荷分配

根据上述扩展蚁群算法形成了M 个机组组合形式，制定相应的稳定最优表，对经济负荷进行分配。

本文主要是采用动态规划法对稳定最优表进行制定，设置阶段变量为x，其表示的是机组工作的台数；决策变量为Nx和状态变量Nx1，其分别表示的是在阶段内工作的机组的出力值与所有机组的出力值总和，则公式为：

式中：f（Nx1）表示的是在x 阶段内所有机组的出力值产生的流量；w（Ni）表示的是机组i 的发电流量。

若是想要使产生的总流量达到最小值，令Nx=Ni，则有方程：

根据上述公式（3）与（4）制定了稳定最优表。然后根据稳定最优表进行经济负荷的分配。最优化原理指出对一个最优策略来说，其下属的决策顺序不会影响策略的优劣，因此，依据稳定最优表进行经济负荷的分配完全合理。

经济负荷分配首先设定水电站的机组数为n，其负荷要求为N，当一组机组开机的时候，其他机组要处于关机的状态。

按顺序从稳定最优表的第一行开始进行搜索，计算每行相应的每个机组的出力值与相应的耗水量，直到搜索到稳定最优表的最后一行结束[4]。

根据上述的机组组合优化与经济负荷分配实现了水电站整体时空经济运行模型的运行。

2 实验结果与分析

为了保证本文构建的大型水电站整体时空经济运行模型的有效性，设计实验对其进行验证。实验过程中，将水电站机组组合与经济符合作为实验对象，对剧组组合以及经济符合进行最优分配。为了保证实验的有效性，使用传统水电站经济运行模型与本文构建的大型水电站整体时空经济运行模型进行比较，观察试验结果。

为了保证实验过程与结果的准确性，对实验过程中的参数进行设置。由于本文采用的是两种不同的模型对水电站机组以及经济符合进行优化，因此，为了最大限度的保证实验结果的精确性，对实验外环境参数进行统一的设置，这样既可以保证实验的准确性，又方便实验的进行。本文外部环境参数设置结果见表1。

表1 外部环境参数设置结果

在实验过程中，由于采用的水电站经济运行模型不同，因此，本文引用第三方软件对其实验数据进行记录与分析。设置传统水电站经济运行模型为对照组，本文构建的大型水电站整体时空经济运行模型为实验组。本文以青岛一大型水电站为研究对象，将一天分为六个时间段，并对他们的用电情况进行预测，结果见表2。

表2 用电功率预测情况

由表 2 可知，一般在 16：00～20：00 为用电高峰期，用电功率最大，达到 1366.58 W,20：00～24：00 耗电量最低，用电功率仅为 301.54 W，是16：00～20：00 的四分之一。分析对照组与实验组预测功率，能够明显看出，实验组预测功率与实际数值基本吻合，对照组具有很大差别，是实验组的八十多倍。说明实验组模型能够很好的预测大型水电站的作用。

采用传统方法和本文方法对青岛一大型水电站的运行效率进行计算，实验结果见图1。

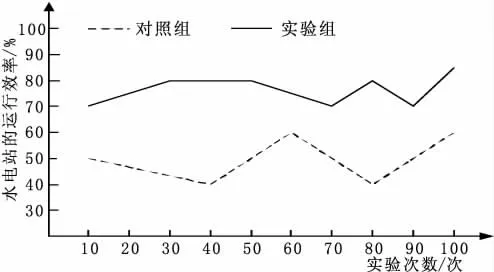
图1 实验对比结果

分析图1 可知，实验组的对照效率幅度变化不大，在50次之前，水电站的运行效率一直缓慢上升，当次数超过50次时出现轻微下降，超过70 次之后，出现一定波动，运行效率基本都在70%以上；对照组在前40 次实验中，运行效率持续下降，40 次到60 次时，运行效率出现上涨并达到峰值60%，随着实验次数的增加，运行效率曲线上下波动，一直没有超过60%；对比实验组与对照组曲线可知，实验组的运行效率明显高于对照组的运行效率，实验组的运行效率最高可以达到85%，而对照组的运行效率最高为60%，实验组的平均运行效率比对照组的平均运行效率高出了25%，说明构建的大型水电站整体时空经济运行模型具备极高的有效性。

3 结语

大型水电站整体时空经济运行模型主要考虑两个方面：（1）时间最优化。对水电站中的机组组合进行优化，使机组组合在运行中满足约束条件，达到最小耗电量；（2）空间最优化。对经济负荷进行分配，使水电站的发电流量达到最小。大型水电站整体时空经济运行模型很大程度上提升了水电站的经济运行效率，值得推广使用。