Camshift目标跟踪算法改进研究
王伟程
(上海理工大学,上海 200093)
运动目标跟踪一直是计算机视觉研究领域的热门课题之一,它是视频监控和安防系统中不可或缺的一部分。传统的目标跟踪方法通常存在着鲁棒性和实时性的矛盾,一般情况下,在视频图像序列中,被跟踪的物体存在着旋转、被遮挡、与背景相融合等现象,在进行目标跟踪时,利用简单的模板匹配方法难以达到理想的效果,且容易出现误匹配和目标跟踪丢失等情况。
目前,传统的Camshift算法被用来解决上述问题,该算法利用目标的颜色直方图表示目标颜色概率出现的大小,目标的颜色直方图仅和目标自身的颜色相关,不受其形状变化的影响,可以有效地解决物体变形的问题。虽然传统的Camshift算法原理简单,运算效率高,然而却无法很好地处理物体被遮挡或与背景融合等情况。针对传统的Camshift算法的不足之处,本文在传统Camshift目标跟踪方法的基础上,提出了Kalman滤波算法预测运动目标位置和粒子滤波算法进行目标中心位置校正的Camshift改进算法,并通过实验验证了该算法的有效性和鲁棒性。
1 Camshift算法
Camshift算法是对Mean-Shift算法的改进,Camshift算法能够根据目标的形变大小自动调节搜索窗口大小来适应目标尺寸的变化,从而可以有效地避免物体形变导致的目标丢失情况,Camshift算法主要包括反向投影、Mean-Shift算法、自适应迭代过程[1]。
Camshift算法以视频图像中目标的颜色信息作为特征,对输入的每帧图像分别作Mean-Shift运算,并将上一帧得到的目标中心和搜索窗口大小[2]作为下一帧Mean-Shift算法的目标中心和搜索窗口大小的初始化值[3],进行迭代运算,直到迭代终止或满足搜索要求为止,实现了目标的连续跟踪。
1.1 反向投影
RGB颜色空间对光照亮度变化敏感,在目标跟踪中为了减少光照强度变化对目标跟踪的影响,将目标图像由RGB颜色空间映射到HSV颜色空间进行处理。HSV颜色空间中的H表示物体颜色色调,它直观地反映了物体的颜色信息,根据图像中H统计的颜色色调目标直方图,计算得到目标图像的颜色概率查找表。将输入的每帧图像的像素值用颜色概率查找表中对应的值进行替换,并归一化到[0, 255]像素值范围内,从而得到图像的颜色概率分布,如图1所示,图像反向投影颜色概率分布是一张灰度图。

图1 图像反向投影颜色概率分布示意
1.2 Mean-Shift算法
Mean-Shift算法是一种非参数密度梯度估计算法[4],它根据搜索框的样本点反复迭代搜索目标图像特征空间中样本点最密集的区域,搜索点沿着样本点密度增加最快的方向“漂移”到局部密度极大值点处,Mean-Shift算法设立1个“漂移”阈值和迭代终止条件,从而寻找到目标位置。Mean-Shift算法原理简单、计算复杂度小,算法流程示意如图2所示。实现的过程包括如下步骤:
1) 设置搜索窗的初始大小和位置。
2) 计算搜索窗的重心。
3) 将搜索窗的中心设置在重心处,迭代移动搜索框的重心到质心处。
4) 每帧图像重复步骤2)和3),直至迭代收敛或迭代计算的搜索窗质心移动的距离小于设定的移动阈值。设I(x,y)是图像概率分布图中位于(x,y)处的像素值,则有:

1.3 自适应迭代过程
Camshift算法是对视频序列中每帧图像分别作Mean-Shift运算,将位置结果和目标大小作为下一帧Mean-Shift算法搜索窗位置的中心和搜索框大小的初始化值[5],进行迭代运算以实现对视频图像中目标的持续跟踪。
1.4 粒子滤波算法
粒子滤波算法又被称为条件概率密度传播算法,核心思想是用状态空间传播的随机样本对概率密度函数进行近似计算[6],以样本均值结果替代积分结果,从而获得状态最小方差分布的过程。当样本容量很大时,该方法近似于状态变量的真实后验概率分布,从而接近最优的贝叶斯估计。
状态转移方程如式(1)所示:
x(t)=f(x(t-1),u(t),w(t))
(1)
观测方程如式(2)所示:
y(t)=h(x(t),e(t))
(2)
式中:x(t)——粒子的t时刻状态;u(t)——控制量;w(t),e(t)——状态噪音和观测噪音。开始时,由于初始状态x(0)没有前项参考值,因此认为x(0)平均地分布在整个状态空间;然后将所有采样值代入状态转移方程中,得到初始化预测粒子。
粒子滤波算法主要包括下面几个阶段:
1) 预测阶段。粒子滤波算法根据x(t-1)的概率分布情况生成大量的采样,样本点即为粒子,根据状态转移方程和控制量可以得到每个粒子的预测粒子。
2) 校正阶段。观测值y到达后,利用观测方程即条件概率P(y|xi)对所有的粒子进行评价。条件概率指: 假设真实状态x(t)取第i个粒子xi时,获得观测y的概率值,令P为第i个粒子的概率值,然后计算图像帧的所有粒子的概率值,从而得到每个粒子的概率值。
3) 重新采样。根据粒子退化程度判断是否需要重新采样,重新采样的目的是去除概率低的粒子,尽可能地复制概率高的粒子,从而估算出需要的真实状态x(t)。重新采样后的粒子集对应真实状态的概率分布情况,再次迭代滤波时,将重新采样后的粒子集输入到状态转移方程中,即可得到预测粒子集。
粒子滤波算法根据粒子和目标的相似性,不断地更新粒子的权重,在粒子退化严重时,须重新采样。从上面的算法和图2所示的流程图中可以看出,粒子滤波的计算复杂度随着粒子数目的增加而增加。相比于Mean-Shift算法,粒子滤波算法拥有较好的跟踪鲁棒性。
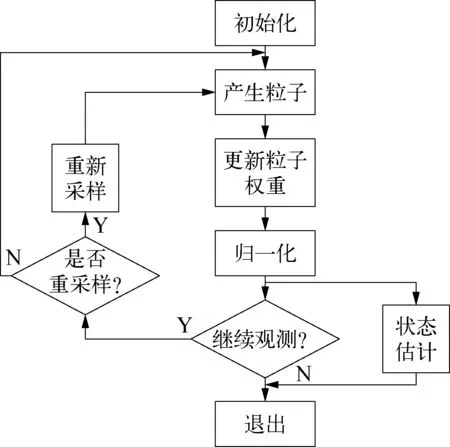
图2 粒子滤波算法流程示意
2 算法改进
Camshift算法复杂度低、计算量小,具有良好的实时跟踪性。当目标被遮挡时,Camshift算法跟踪目标易发生错误,会造成跟踪目标丢失的情况。针对Camshift算法的不足之处,文中提出了一种改进的Camshift算法[7]。运用Kalman算法预测当前帧目标的中心位置,并结合粒子滤波算法校正搜索目标中心[8]。
1) 运用Kalman算法预测当前帧目标的中心位置,并对每帧图像进行Camshift运算,将得到的实际结果反馈给Kalman滤波器修正参数[9],进而预测跟踪目标的下一帧位置[3],形成1个目标位置反馈环路。利用Kalman滤波改进的Camshift算法[10-11]如图3所示。
2) 跟Camshift算法相比,根据Kalman算法改进的Camshift算法[9]在物体被遮挡时能有效地跟踪到物体,拥有更强的跟踪鲁棒性。然而,由于Kalman的预测是基于物体前期状态进行预测,当跟踪物体被长时间遮挡或改变运动路径时,由Kalman算法改进的Camshift算法难以在被跟踪物体再次出现时进行有效跟踪[10]。针对该问题,本文引入粒子滤波算法进行目标中心位置校正,粒子滤波的改进作用是在物体长时间被遮挡后当再次出现时能被快速的捕捉,并把粒子滤波计算得到的期望位置反馈给Camshift算法,完成后续跟踪,达到增强跟踪鲁棒性的作用,改进算法流程如图4所示。
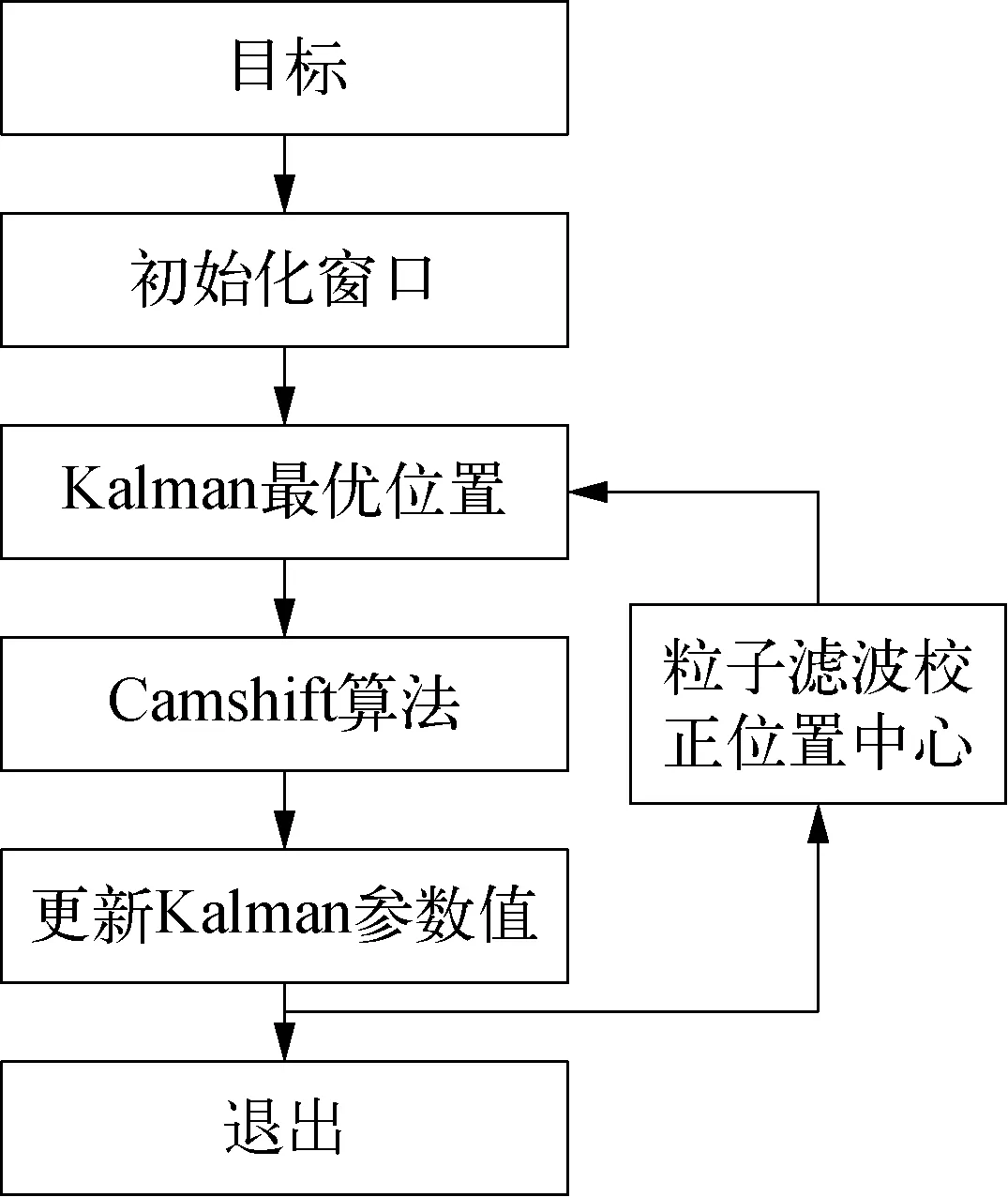
图4 改进的Camshift算法示意
首先初始化目标图像窗口,标定待跟踪物体,初始化Kalman滤波器,在Kalman期望的位置附近使用Camshift算法搜索目标图像,把检测到的目标图像的实际位置反馈给Kalman滤波器更新Kalman参数值。在连续的视频帧中,每10帧图像使用粒子滤波算法计算目标期望中心,并把期望中心对Kalman的期望中心进行一次参数校正处理,对于长时间遮挡的物体,当它再次出现时能够及时有效地校正Kalman的中心,使得长时间遮挡的物体再次出现时能够得到有效的跟踪。
3 实验结果及分析
软件调试环境为visual studio 2017,图5~图7显示了运动目标跟踪的情况,图中标定的物体是方形盒子,最大的方框是Kalman滤波算法和粒子滤波算法改进的Camshift算法跟踪物体搜索出的矩形框,细框代表单个粒子滤波粒子产生的期望方框。
3.1 不规则运动
跟踪物体在平面内做不规则运动,通过图5所示的4幅图像可以看出,改进的算法能够很好地跟踪平面内的运动物体,并没有造成丢失和误匹配等问题。该实验表明: 改进的算法能够有效地跟踪不规则运动物体。
3.2 运动物体被遮挡的情况下和传统的Camshift算法比较
图6~图7中的4幅图像分别代表物体未被遮挡、物体被半遮挡、物体被完全遮挡以及物体被遮挡后再次出现时算法对物体的跟踪情况,图6表示使用传统的Camshift跟踪算法,图7表示使用改进的Camshift跟踪算法。可以看出,随着物体被遮挡程度的提高,传统的Camshift算法对物体的跟踪能力越来越差,而本文提出的改进Camshift算法始终可以有效地跟踪物体。另外,当物体被遮挡后再次出现时,传统的Camshift算法未能准确地跟踪到物体,而本文提出的改进Camshift算法可以实现该功能。

图6 传统Camshift跟踪算法示意

图7 改进Camshift跟踪算法示意
实验结果表明: 与传统的Camshift算法比较可以看出,改进的Camshift算法具有更强的鲁棒性,传统的Camshift算法容易发生错误的跟踪,当物体长时间被遮挡后,被跟踪物体再次出现时,传统的Camshift算法未能成功检测并重新跟踪。因此,改进的Camshift算法在鲁棒性和稳定性上优于传统的Camshift算法。
4 结束语
本文提出了结合Kalman滤波和粒子滤波算法改进的Camshift算法,该算法在跟踪实验中表现出良好的跟踪性能。该算法首先在Camshift算法基础上利用Kalman对搜索窗口进行运动位置预测,然后引入粒子滤波算法校正Camshift的目标中心位置。实验结果表明: 改进的Camshift算法可以在不影响跟踪实时性的前提下有效提高目标跟踪的鲁棒性。

