墩台沉降对桥上纵连板式无砟轨道线路动力影响

徐庆元， 张 泽， 方子匀， 娄 平， 林青腾， 李 伟

(中南大学 土木工程学院，长沙 410075)

墩台不均匀沉降控制是高速铁路桥上纵连板式无砟轨道的关键技术，高速列车在墩台不均匀沉降地段高速行驶时，不但旅客的舒适性会受到影响，而且在墩台不均匀沉降与列车等荷载组合作用下，墩台不均匀沉降地段桥上无砟轨道结构有可能因结构抗力不足而失效破坏[1]，从而严重影响桥上无砟轨道结构的耐久性和高速列车运行的安全性。因此，在墩台不均匀沉降下，研究桥上纵连无砟轨道线路的动力特性，对工程建设至关重要。

目前，国内虽对列车-纵连板式无砟轨道-桥梁耦合系统的动力特性做了大量研究[2-3]，但研究大多没有考虑墩台不均匀沉降的影响。文献[4-5]研究了墩台不均匀沉降对桥上纵连板式无砟轨道力学特性的影响，但研究采用的模型是静力模型。文献[6]基于列车-桥梁耦合动力学理论，以高速列车通过桥上不同幅值的墩台沉降线路地段为例，对列车和桥梁结构耦合振动特性的动力仿真进行了研究，但文献[6]所采用的仿真模型既没有考虑无砟轨道结构的影响，也没有考虑墩台不均匀沉降对桥上无砟轨道动力特性的影响。

本文借鉴国内外列车-轨道-桥梁耦合动力学理论[7-8]和组合荷载下无砟轨道动力特性[9-10]的研究成果，考虑纵连板式轨道-桥梁系统各部件间接触状态非线性，建立了高速列车-纵连板式无砟轨道-桥梁三维非线性有限元耦合动力学模型，并在此基础上深入研究列车高速通过墩台不均匀沉降地段时，无砟轨道各部件动应力特性及耦合系统振动特性。

1 高速列车-纵连板式无砟轨道-桥梁三维非线性有限元耦合动力学模型

高速列车-纵连板式无砟轨道-桥梁三维非线性有限元耦合动力学模型由3个子模型组成，分别为高速动车组子模型、纵连板式无砟轨道-桥梁子模型及连接两个子模型的轮轨关系子模型，这3个子模型详细介绍如下：

1.1 高速动车组子模型

机车车辆采用在我国高速铁路上大量使用的CRH3高速列车。高速动车组由动车和拖车编组而成，对于每一节动车和拖车，其力学模型如图1所示。在图1中，以多刚体模拟车体、转向架和轮对，以弹簧-阻尼单元模拟车体与转向架、转向架与轮对间的连接。由于墩台沉降主要影响列车的垂向动力响应，本文高速动车组子模型只考虑与列车垂向振动相关的自由度，即车体和转向架考虑沉浮、点头自由度，轮对考虑沉浮自由度。对于每节动车和拖车，模型有10个自由度，而对于高速动车组，模型则有10*m个自由度(m为动车组动车和拖车总个数)。

图1 车辆动力学模型Fig.1 Vehicle dynamic model

1.2 纵连板式无砟轨道-桥梁子模型

利用前文所述耦合动力学模型，计算高速列车在桥上纵连板式无砟轨道线路上高速运行下的耦合系统振动时程曲线及无砟轨道各部件动应力时程曲线，通常具有非常大的计算量和相当长的计算时间。其主要原因如下：首先，为了提高无砟轨道各部件动应力的数值仿真精度，本文采用20节点三维实体单元对轨道板、底座板和桥梁进行模拟，并且采用较细的网格，因此模型自由度较多；其次，模型中所用高速列车长度达到200 m，而为了得到完整的耦合系统振动时程曲线和无砟轨道各部件动应力时程曲线，列车要移动很长的距离，例如本文高速列车移动距离为300 m；最后，扣件间距对耦合系统动力特性的影响不可忽略，因此仿真步长不可过大，本文仿真计算时每步移动0.05 m。

为了减少计算工作量，拟对纵连板式无砟轨道-桥梁子模型采用多尺度建模。多尺度子模型中间部分采用网格较细密、计算速度较慢、计算精度高的三维单元建模，两端部分采用梁单元和弹簧单元建模，中间和两端连接部分采用网格相对较粗、计算速度相对较快、计算精度相对较差的三维单元建模。同时，本文还采取以下两个措施来进一步减少系统自由度：一方面，根据刚度和质量等效的原则，将实际桥梁断面简化为矩形断面；另一方面，利用模型的对称性，在模型对称轴上施加对称边界条件建模。

本文在ANSYS通用有限元软件环境下建立了多尺度纵连板式无砟轨道-桥梁子模型。考虑仿真速度和精度的平衡，桥梁总跨数取为4跨，其总体图及其大样图(第1、2桥跨连接处)分别见图2和图3。在上述子模型中，钢轨以beam4梁单元模拟，中间2跨桥梁及其上的轨道板和底座板采用计算速度较慢但精度高的solid95三维实体单元，边上2跨桥梁及其上的轨道板和底座板采用计算速度较快但精度相对低的solid45三维实体单元。

图2 多尺度纵连板式无砟轨道-桥梁子模型总体图Fig.2 Overall view of multi-scale sub-model of longitudinal connected slab track-bridge

钢轨与轨道板之间连接以combin14弹簧-阻尼单元模拟。在边上2跨桥梁区域内，每个钢轨节点与具有相同纵横向坐标的相应轨道板上表面节点相连，在中间2跨桥梁区域内，每个钢轨节点与轨道板上表面位于扣件尺寸区域内的所有节点全部相连，来考虑无砟轨道结构力学特性受扣件尺寸效应的影响。

图3 多尺度纵连板式无砟轨道-桥梁子模型大样图Fig.3 Enlarged view of multi-scale sub-model of longitudinal connected slab track-bridge

在边上和中间2跨桥梁范围内，轨道板与底座板之间连接分别采用combin14弹簧-阻尼单元和conta178 接触单元模拟，combin14和conta178参数取值由CA砂浆弹性模量及厚度换算确定。

底座板与桥梁之间连接选用combin14弹簧-阻尼单元模拟。为了考虑底座板与桥梁间滑动层和梁端处挤塑板刚度阻尼差异，本文根据挤塑板刚度和阻尼换算得到梁端处挤塑板范围内combin14弹簧-阻尼单元的参数取值，而模拟挤塑板范围外滑动层的combin14弹簧-阻尼单元参数则取相对较大值。

桥上纵连板式无砟轨道混凝土在列车、温度梯度、温度等组合荷载循环作用下，不可避免要开裂，而无砟轨道中连续配置的纵向钢筋使得开裂后无砟轨道仍可传递较大的竖向剪力。为此，选用刚度较大的竖向弹簧单元来连接裂缝两侧混凝土单元。

为模拟裂缝，轨道板和底座板在裂缝处生成两个坐标相同的节点，而在非裂缝处，轨道板和底座板在同一位置处只生成一个节点。由于轨道板和底座板在裂缝处同一位置有两个坐标相同的节点，因而在图2～图3所示力学模型中，裂缝无法显示，但裂缝是真实存在的。

对于裂缝间距，本文以现场调研的桥上纵连板式无砟轨道裂缝间距为依据，并参考国内外采用连续配筋的无砟轨道及水泥混凝土路面裂缝间距研究成果，裂缝间距考虑1、2倍扣件间距两种情况。

1.3 轮轨关系子模型

轮轨关系子模型如图4所示，轮轨间的作用力大小可根据赫兹非线性弹簧接触理论确定：

(1)

式中：G为轮轨接触常数，m/N2/3；Zw(j，t)为t时刻时第j个车轮的垂向位移，m；Zr(j，t)为t时刻时第j个车轮下钢轨的垂向位移，m；Z0(t)为轮轨界面之间竖向不平顺，在平顺状态下值为0。

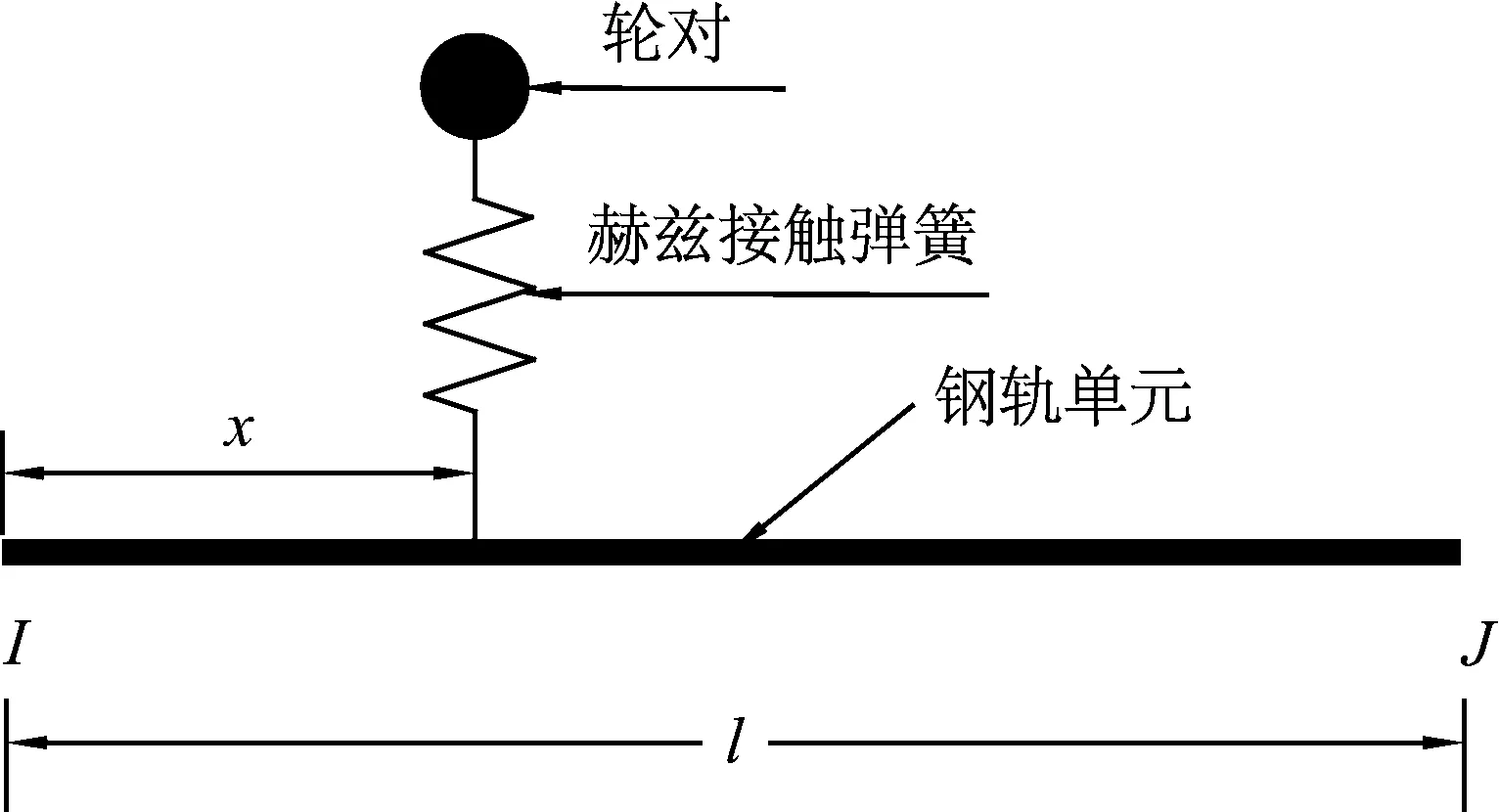
图4 轮轨关系子模型Fig.4 Sub-model of wheel-rail interaction

2 高速列车-纵连板式无砟轨道-桥梁耦合动力学荷载模型

高速列车-纵连板式无砟轨道-桥梁耦合系统动力特性，特别是动应力和位移特性与列车自重荷载有很大的关系。本文在高速动车组各部件的质心处施加等同于该部件自重的集中荷载来模拟这一工况。

为了突出墩台不均匀沉降对高速列车-纵连板式无砟轨道-桥梁耦合系统动力特性的影响，本文不把轨道随机不平顺纳入考虑范围，只是在桥梁中间的桥墩处施加不同幅值垂向位移来模拟墩台不均匀沉降。

另外，由于墩台不均匀沉降，无砟轨道各部件间、无砟轨道与桥梁间也许会由于变形不协调而出现局部脱空，高速列车经过脱空地段时会引起很强烈的列车-轨道-桥梁系统耦合振动。由于脱空范围与程度和无砟轨道自重有一定关系，本文建立的高速列车-纵连板式无砟轨道-桥梁耦合系统动力学模型还研究了无砟轨道的自重荷载。

3 高速列车-纵连板式无砟轨道-桥梁耦合动力学模型求解

由于本文所建立的高速列车-纵连板式无砟轨道-桥梁耦合动力学模型的自由度超过了60万，因此如何快速对耦合系统振动方程进行求解极其重要。经过研究，相比大型稀疏矩阵的直接求解算法，预处理共轭梯度法(Preconditioned Conjugate Gradient method，PCG)具有一定的优势[11]，本文采用PCG法进行大型稀疏矩阵的快速求解，使得高速列车-纵连板式无砟轨道-桥梁耦合系统动力仿真研究在普通微机上实现成为可能。

4 高速列车-纵连板式无砟轨道-桥梁三维有限元耦合动力学模型验证

采用本文所建的耦合动力学模型，计算列车以393 km/h在桥上线路高速运行时，轨道板和桥梁梁体的垂向加速度。张卫华[12]对CRH3型高速动车组以393 km/h在京津城际客运专线上运行时，轨道板和桥梁的振动数据进行了现场实测，实测轨道板的垂向加速度为1.5～2.5 g，桥梁梁体垂向加速度为0.05～0.09 g。模型计算得到的轨道板垂向加速度时程曲线、桥梁梁体垂向加速度时程曲线见图5(a)和图5(b)。

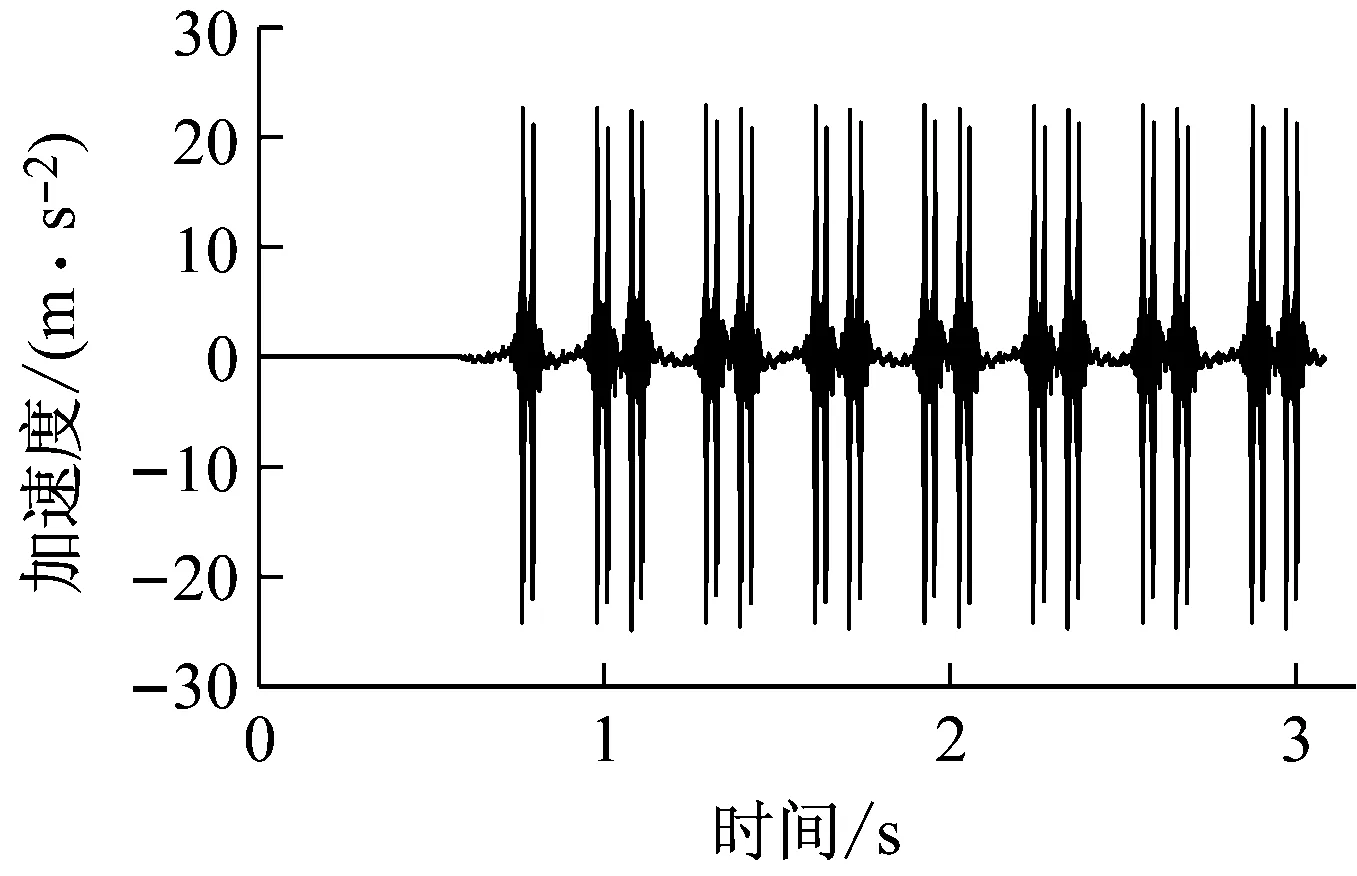
(a) 轨道板

(b) 桥梁图5 轨道板和桥梁垂向加速度时程曲线Fig.5 Vertical acceleration history of slab and bridge

根据图5能够得出，轨道板、桥梁梁体垂向加速度计算值与实测值较为符合，验证了本文所建耦合动力学模型和编制程序的正确性。

5 计算算例

5.1 计算条件

8节动车组全长200 m，由于本文只研究中间2跨桥梁及其上无砟轨道的动力特性，开始运行时，动车组第一轮对位于第一跨桥中点位置，动车组最后位轮对位于距离第一跨桥前184.4 m的路基上，动车组以300 km/h速度在32 m多跨简支箱梁桥上纵连板式无砟轨道线路墩台不均匀沉降地段运行，轨道和桥梁主要动态计算参数如表1所示，高速动车组参数详见文献[2]。一共考虑8种墩台不均匀沉降工况，如表2所示。

5.2 仿真计算结果

采用本文建立的耦合动力学模型，对上述8种工况进行仿真计算，当裂缝间距为1倍和2倍扣件间距时，墩台不均匀沉降对车体最大加速度、最大垂向轮轨力、钢轨最大垂向加速度、钢轨最大正弯矩、扣件最大压力、扣件最大拉力、轨道板最大垂向加速度、轨道板纵向最大拉应力、底座板最大垂向加速度、底座板纵向最大拉应力、CA砂浆最大压应力、桥梁最大垂向加速度的影响规律,分别如图6～图17所示。

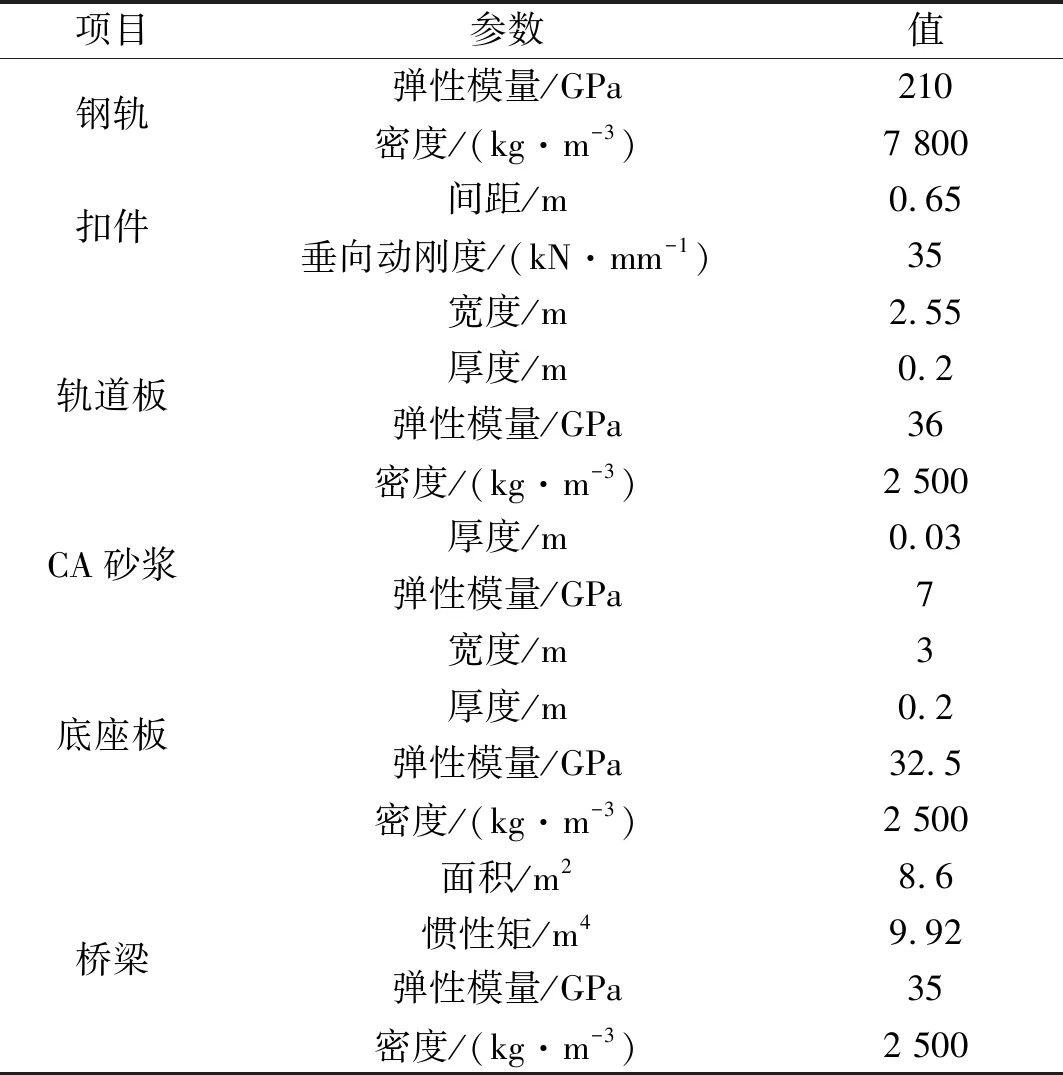
表1 轨道和桥梁计算参数Tab.1 Calculation parameter of track and bridge

表2 仿真计算方案Tab.2 Scheme and plans for the simulation

5.3 计算结果分析

(1) 分析图6可知，车体最大加速度与墩台不均匀沉降有很大的关系，车体最大加速度随着墩台不均匀沉降的增加而快速增加。与平顺线路相比，墩台不均匀沉降达到30 mm时，车体最大加速度增大了近16倍。不同墩台沉降幅值下车体最大加速度受无砟轨道裂缝间距的影响不大。

(2) 由图7易知，最大垂向轮轨力与墩台不均匀沉降存在一定相关关系，最大垂向轮轨力随着墩台不均匀沉降的增加而增加。相比平顺状态，墩台不均匀沉降达到30 mm时最大轮轨力增加了近16%。墩台不均匀沉降对最大垂向轮轨力的影响与无砟轨道裂缝间距关系不大。

(3)
图8表明，钢轨最大竖向加速度与墩台不均匀沉降有很大关系，随着墩台不均匀沉降的增加，钢轨最大垂向加速度也随之增加。相比平顺状态，墩台不均匀沉降为30 mm时钢轨最大垂向加速度增加了近17倍，超过20 g。不过，对于实际线路，钢轨振动主频主要由轨道随机不平顺引起，其频率成分主要集中在高频且振动加速度幅值高达数百g，因而，由墩台不均匀沉降引起的钢轨最大垂向加速度幅值要远远小于实际钢轨振动加速度幅值。

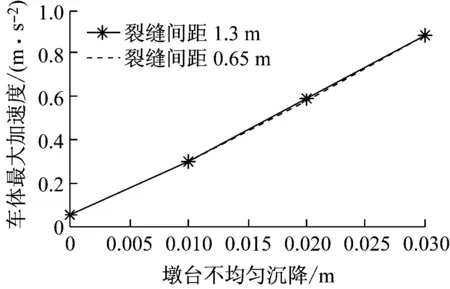
图6 不同沉降幅值下车体最大加速度

Fig.6 Maximum acceleration of car body under different settlement of abutments and piers

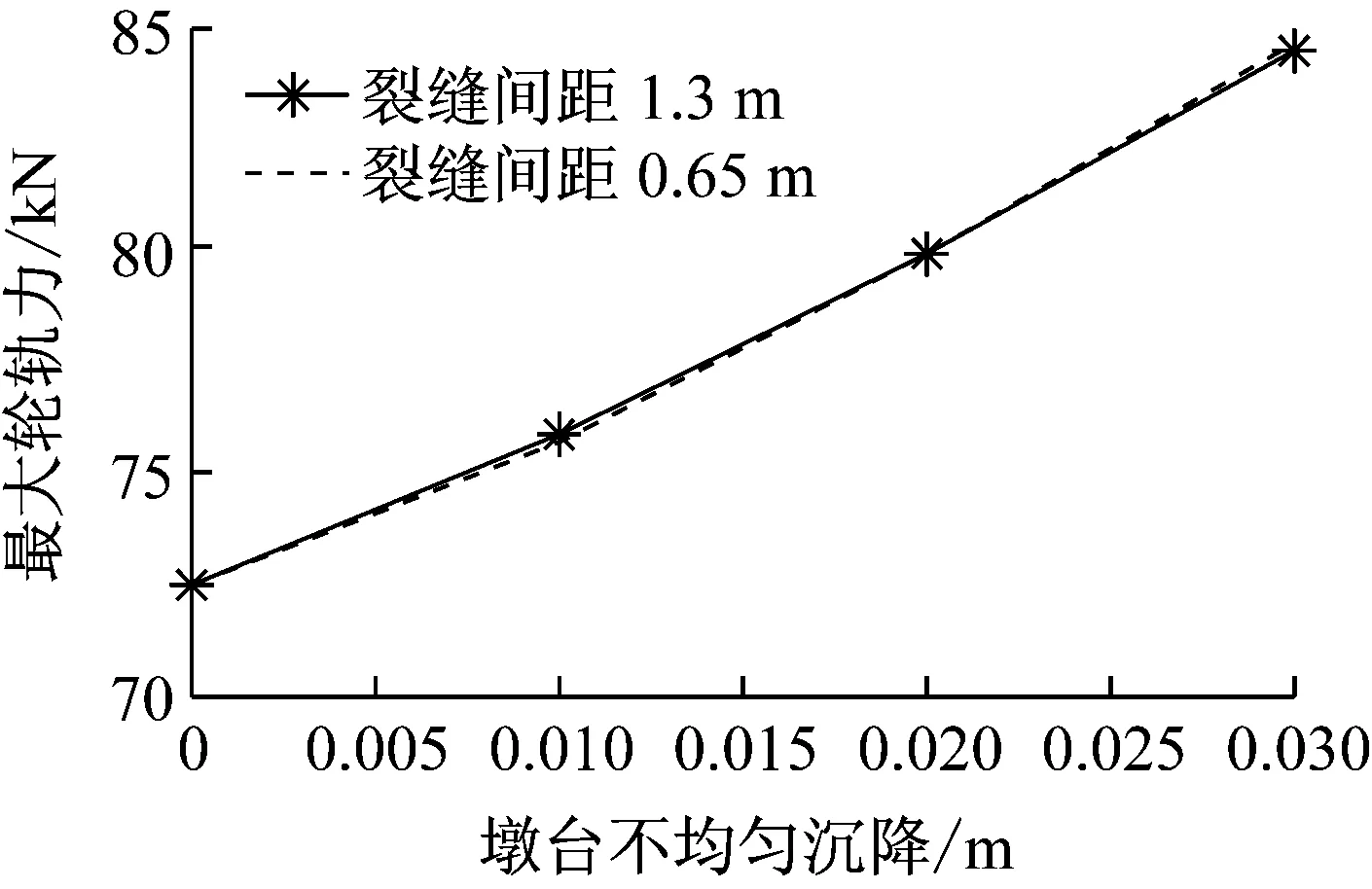
图7 不同沉降幅值下最大垂向轮轨力

Fig.7 Maximum vertical wheel-rail force under different settlement of abutments and piers

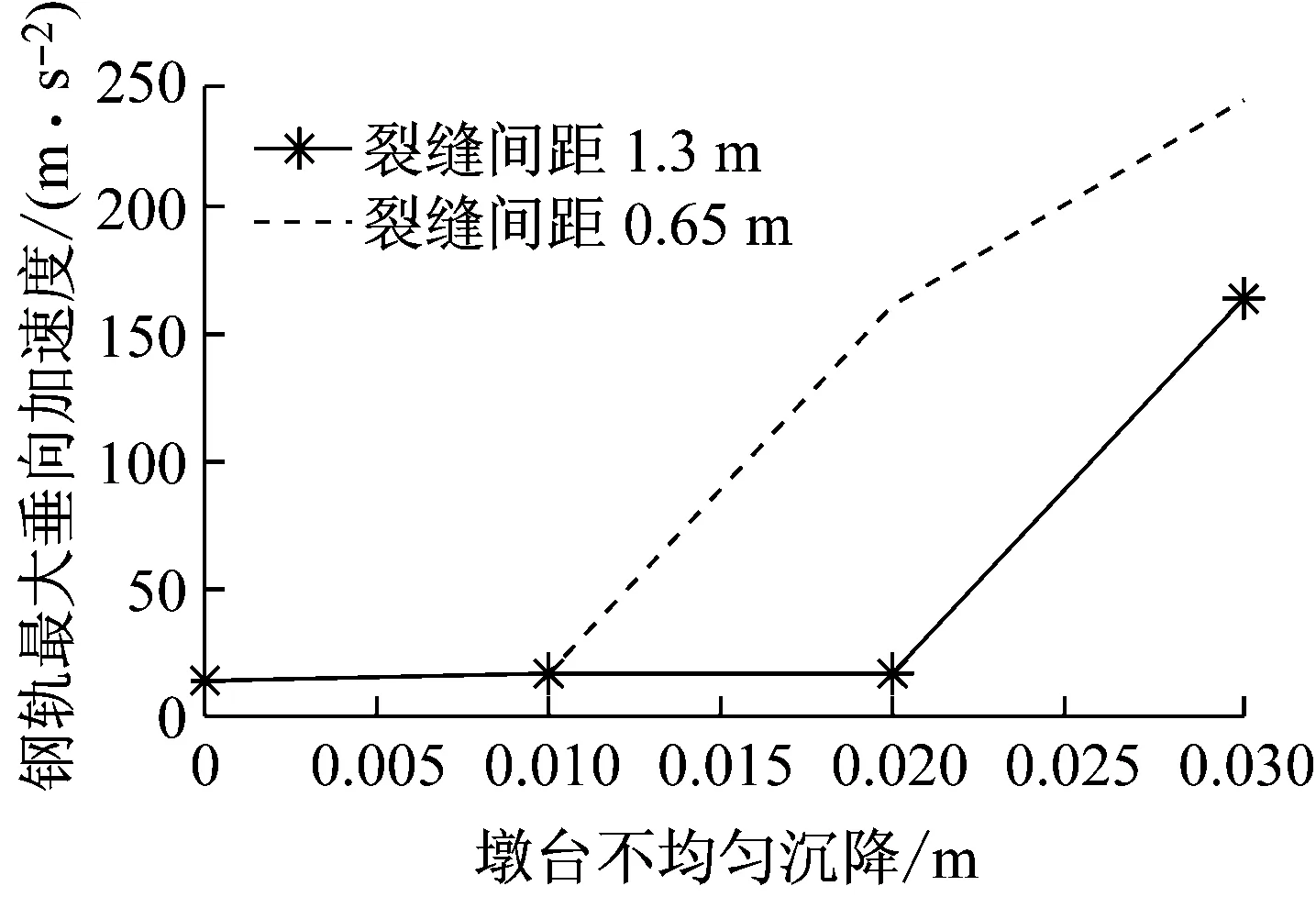
图8 不同沉降幅值下钢轨最大垂向加速度

Fig.8 Maximum vertical acceleration of rail under different settlement of abutments and piers

图9 不同沉降幅值下钢轨最大正弯矩

Fig.9 Maximum positive bending moment of rail under different settlement of abutments and piers

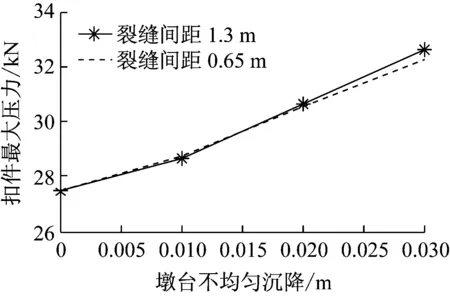
图10 不同沉降幅值下扣件最大压力

Fig.10 Maximum pressure force of fastener under different settlement of abutments and piers

图11 不同沉降幅值下扣件最大拉力

Fig.11 Maximum tensile force of fastener under different settlement of abutments and piers

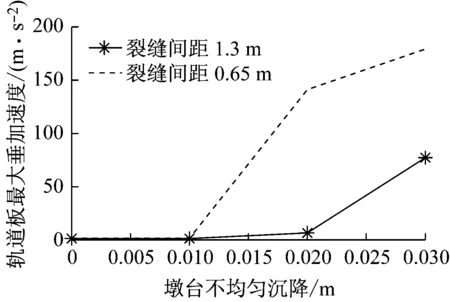
图12 不同沉降幅值下轨道板最大垂向加速度

Fig.12 Maximum vertical acceleration of slab under different settlement of abutments and piers

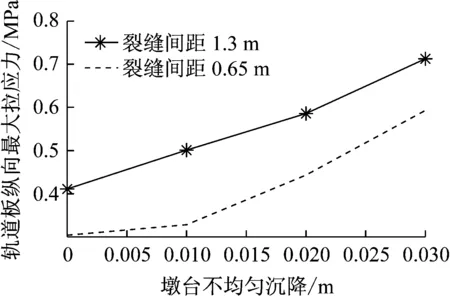
图13 不同沉降幅值下轨道板纵向最大拉应力

Fig.13 Maximum longitudinal tensile stress of slab under different settlement of abutments and piers

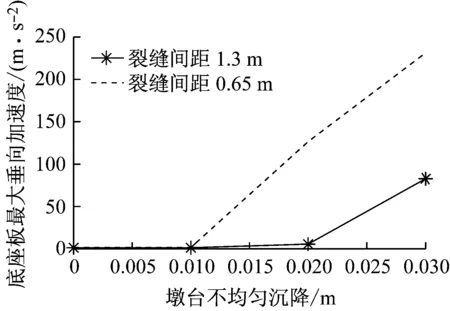
图14 不同沉降幅值下底座板最大垂向加速度

Fig.14 Maximum vertical acceleration of base plate under different settlement of abutments and piers

图15 不同沉降幅值下底座板纵向最大拉应力

Fig.15 Maximum longitudinal acceleration of base plate under different settlement of abutments and piers

图16 不同沉降幅值下CA砂浆最大压应力

Fig.16 Maximum pressure stress of CA mortar under different settlement of abutments and piers

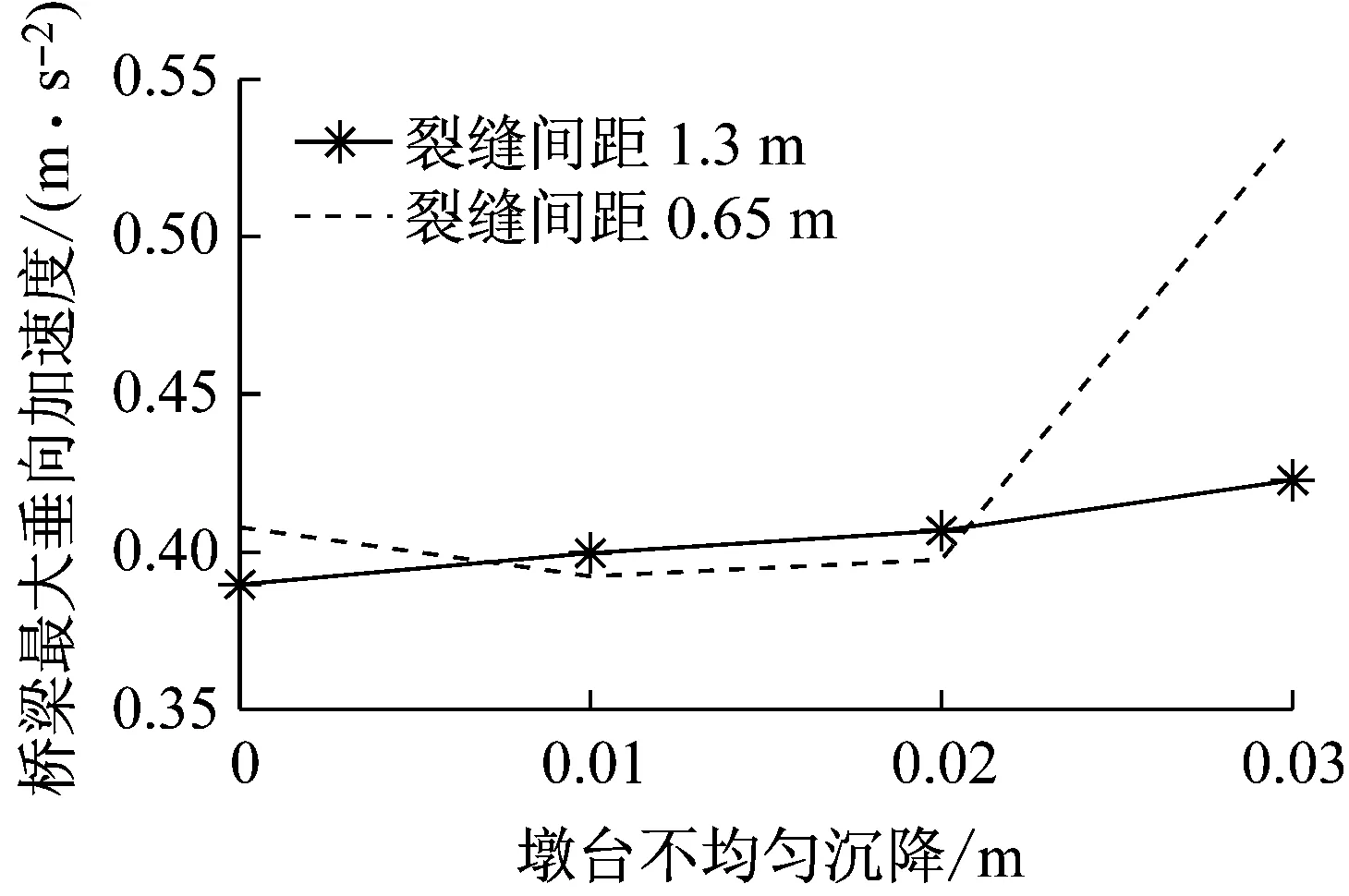
图17 不同沉降幅值下桥梁最大垂向加速度

Fig.17 Maximum vertical acceleration of bridge under different settlement of abutments and piers

(4) 由图9可知，钢轨最大正弯矩与墩台不均匀沉降有较大的关系，钢轨最大正弯矩随着墩台不均匀沉降的增加而有较大幅度的增加。相比平顺状态，墩台不均匀沉降为30 mm时钢轨最大正弯矩增幅在65%左右。无砟轨道裂缝间距对墩台不均匀沉降下钢轨的最大正弯矩影响不大。

(5) 分析图10可知，扣件最大压力与墩台不均匀沉降有一定的关系，随着墩台不均匀沉降的增加，扣件最大压力也随之增加。相比平顺状态，墩台不均匀沉降为30 mm时扣件最大压力增加幅度在18%左右。无砟轨道裂缝间距对墩台不均匀沉降下扣件最大压力的影响不大。

(6) 从图11可以看出，扣件最大拉力与墩台不均匀沉降有很大的关系，随着墩台不均匀沉降的增加，其值也快速增加，且增幅与无砟轨道裂缝间距有一定的关系。相比平顺状态，墩台不均匀沉降为30 mm时扣件最大拉力增加幅度，当裂缝间距为0.65 m时在142%左右，当裂缝间距为1.3 m时在204%左右。

(7) 分析图12可以得到如下结论：随着墩台不均匀沉降的增加，轨道板最大垂向加速度也随之增加，增加近58倍，但其变化规律与墩台不均匀沉降和裂缝间距均有关，比较复杂。当裂缝间距为0.65 m时，墩台不均匀沉降在10 mm以内，轨道板最大垂向加速度随着墩台不均匀沉降增加而缓慢增加，随后快速增加；当裂缝间距为1.3 m时，墩台不均匀沉降在20 mm以内，轨道板最大垂向加速度随着墩台不均匀沉降增加而缓慢增加，随后快速增加。主要原因是当墩台不均匀沉降达到一定值时，会引起无砟轨道各部件间、无砟轨道与桥梁之间产生局部的脱空，导致无砟轨道振动急剧增加。从图12还可以看出，对于相同的墩台不均匀沉降，当裂缝间距小时，轨道板振动加速度相对较大，主要原因是裂缝间距小时，无砟轨道质量也小，在外力作用下更容易发生振动。

(8) 从图13可以看出，轨道板纵向最大拉应力与墩台不均匀沉降有较大的关系，随着墩台不均匀沉降的增加，轨道板纵向最大拉应力有较大幅度的增加。相比平顺状态，墩台不均匀沉降达到30 mm时轨道板纵向最大拉应力增加幅度在72%左右。墩台不均匀沉降对轨道板纵向最大拉应力的影响与无砟轨道裂缝间距关系不大。

(9) 分析图14可知，底座板最大垂向加速度也随着墩台不均匀沉降的增加而增加，增加看近64倍，但其变化规律与墩台不均匀沉降和裂缝间距均有一定的关系，比较复杂。当裂缝间距为0.65 m时，底座板最大垂向加速度开始随着墩台不均匀沉降增加而缓慢增加，墩台不均匀沉降超过10 mm以后，底座板最大垂向加速度随着墩台不均匀沉降增加而快速增加；当裂缝间距为1.3 m时，底座板最大垂向加速度开始随着墩台不均匀沉降增加而缓慢增加，墩台不均匀沉降超过20 mm以后，底座板最大垂向加速度随着墩台不均匀沉降增加而快速增加。主要原因是当墩台不均匀沉降超过一定值，会引起无砟轨道-桥梁间局部脱空，导致无砟轨道振动急剧增加。从图14我们还可知，对于相同的墩台不均匀沉降，当裂缝间距小时，由于底座板参振质量小，底座板垂向振动加速度相对较大。

(10)
图15表明，底座板纵向最大拉应力与墩台不均匀沉降有较大的关系，其值随着墩台不均匀沉降的增加而增加，且增加规律与无砟轨道裂缝间距有一定的关系。当无砟轨道裂缝间距为0.65 m时，相比平顺状态，墩台不均匀沉降为30 mm时底座板纵向最大拉应力增加幅度在29%左右，当无砟轨道裂缝间距为1.3 m时，其增加幅度在59%左右。

(11) 对图16加以分析，我们可以得到以下结论：CA砂浆最大压应力与墩台不均匀沉降有较大的关系，其值随着墩台不均匀沉降的增加而大幅增加，且增加规律与无砟轨道裂缝间距有一定的关系。相比平顺状态，墩台不均匀沉降为30 mm时CA砂浆最大压应力的增加幅度，当无砟轨道裂缝间距为0.65 m时在353%左右，当无砟轨道裂缝间距为1.3 m时在61%左右。从图16我们还可以看出，当墩台不均匀沉降小于20 mm时，CA砂浆最大压应力增加比较缓慢，而当墩台不均匀沉降大于20 mm后，CA砂浆最大压应力增加极为迅速，主要原因是较大的墩台不均匀沉降容易引起无砟轨道各部件间、无砟轨道与桥梁间局部脱空，进而使CA砂浆所受的最大压应力迅速增加。

(12) 从图17可以看出，桥梁最大垂向加速度与墩台不均匀沉降关系不大，随着墩台不均匀沉降的增加，桥梁最大垂向加速度仅小幅增加，增幅在10%左右。墩台不均匀沉降对桥梁最大垂向加速度的影响与无砟轨道裂缝间距关系也不大。

6 结 论

基于耦合动力学理论，考虑纵连板式无砟轨道-桥梁系统各部件间非线性接触，建立高速列车-纵连板式无砟轨道-桥梁三维非线性有限元耦合动力学模型，并利用此模型深入研究了高速列车在桥上纵连板式无砟轨道线路墩台不均匀沉降地段高速行驶时，车辆、桥梁振动特性及无砟轨道各部件动应力特性，研究得到以下结论：

(1) 墩台不均匀沉降对高速列车-纵连板式无砟轨道-桥梁耦合系统车体振动加速度增加了16倍、钢轨振动加速度增加了17倍、轨道板及底座板振动加速度甚至分别增加了58倍和64.4倍，墩台不均匀沉降对桥梁振动加速度只增加了10%，影响较小。

(2) 墩台不均匀沉降对最大垂向轮轨力和无砟轨道各部件动应力特性有不同的影响规律。在墩台不均匀沉降作用下，最大垂向轮轨力增加了16%、扣件最大压力增加了18%，且影响规律与无砟轨道裂缝间距关系不大；墩台不均匀沉降对扣件最大拉力、CA砂浆最大压应力以及底座板纵向最大拉应力有较大影响，且影响规律与无砟轨道裂缝间距有一定的关系；墩台不均匀沉降对钢轨最大正弯矩、轨道板纵向最大拉应力有较大的影响，影响幅度在70%左右，且影响规律与无砟轨道裂缝间距关系不大。

(3) 墩台不均匀沉降对高速列车-纵连板式无砟轨道-桥梁耦合系统振动及动应力特性的影响规律并非是简单的单调线性增加，而是与墩台不均匀沉降引起的无砟轨道各部件间、无砟轨道与桥梁间局部脱空有关。本文用接触单元模拟无砟轨道各部件间、无砟轨道与桥梁间连接，可以很好反映这一情况。