GMM高速开关阀用液压放大器建模与实验

罗 樟，朱玉川，高 强

(南京航空航天大学 机电学院,江苏 南京 210016)

0 引言

高速开关阀作为典型的液压数字元件，广泛应用于燃油喷射及飞机刹车等领域，通常由脉宽调制(PWM)数字信号直接驱动，通过调节占空比实现离散化流量的输出，具有压力损失小，油液敏感度低等优势[1]。目前市场上应用的高速开关阀大多采用电磁铁作为电-机转换器，开关频率低于50 Hz，是限制其性能的主要因素之一。将智能材料应用到高速开关阀上，可提高高速开关阀的频响。

超磁致伸缩材料(GMM)作为典型的智能材料，具有输出力大，响应快，能量传输密度高等优点[2]，为构建高频大流量的高速开关阀，采用GMM驱动阀芯，鉴于其输出位移小的特点，需对GMM执行器的输出位移进行放大。

微位移放大器按放大形式可分为柔性铰链放大、压曲放大和液压放大等[3]。柔性铰链放大具有无机械摩擦，动作灵敏度高等优点，但通常要求多级放大以达到相应的放大倍数，这会产生结构复杂，易疲劳损坏，带载能力差等问题。压曲放大和液压放大的结构相对简单，放大能力较高，但前者的输出力小，而后者存在泄漏及动态性能差等问题[4-6]。

Suryarghya Chakrabarti等[7]设计了一种活塞式位移放大的磁致伸缩致动器，并建立了其动态模型。杨朝舒等[8]设计了一种超磁致伸缩直驱式电液伺服阀，利用柔性活塞式的位移放大器对超磁滞伸缩棒的位移进行放大，通过仿真分析其放大倍数可达9倍。本文提出基于活塞-薄片式的流体微位移放大器(简称位移放大器)，并在此基础上开展了相关的理论、仿真与实验研究工作。结果表明，提出的GMM高速开关阀用位移放大器动态性能好，放大倍数高，可为后续研制高频响大流量的高速开关阀提供有价值的参考。

1 结构及工作原理

图1为流体微位移放大GMM驱动器结构原理，由位移放大器和超磁致伸缩执行器(GMA)组成。图中，位移放大器由铍青铜薄片、活塞、活塞和铍青铜片间的液压油和活塞测试杆构成；GMA由输出杆，超磁致伸缩棒和线圈等组成，其中输出杆和活塞固连。其工作原理为：当线圈通电后，线圈内部产生激励磁场驱动GMM伸长，通过输出杆推动活塞向上运动，活塞挤压容腔内油液向小腔内运动，油液挤压铍青铜薄片使其发生变形而产生一定位移，这样可将活塞的位移放大输出。

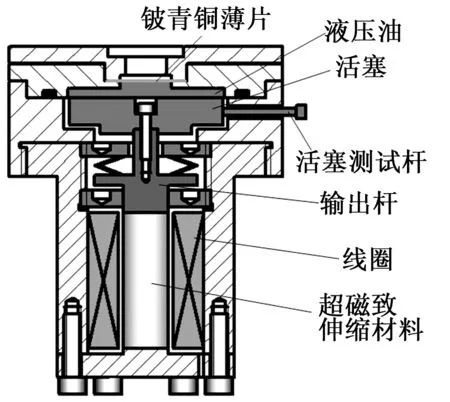
图1 GMM驱动器的结构原理图

2 位移放大器的静态模型

2.1 弹性薄片变形的计算

铍青铜薄板为边缘固定夹紧的弹性圆薄板，最大挠度与其厚度之比大于0.2，经典薄板理论已无法适用[9]，在此利用“钱氏法”以圆薄板中心挠度为摄动参数，求解位移放大器中弹性薄片的变形[10],得到挠曲线方程和最大挠度-压力方程为

(1)

(2)

式中：ω(r)为挠曲线方程；p为作用在薄片上的压力；ωm为最大挠度(即薄片中心挠度)；ω1、ω2、A1、A2为“钱氏法”所得到的多项式和系数；R为薄板半径；r为薄片的径向坐标。

将式(1)、(2)的计算结果与ANSYS仿真结果进行对比。图2为同一薄片在ωm分别为0.08 mm、0.16 mm、0.25 mm、0.34 mm挠曲线形状的ANSYS仿真结果和“钱氏法”计算结果的对比。由图 可知，当中心挠度为0.08 mm时，“钱氏法”与ANSYS仿真得到的挠曲线基本重合;当中心挠度为0.25 mm和0.34 mm时，“钱氏法”得到的挠曲线出现了中心下凹的情况，这和ANSYS仿真的挠曲线形状不符。

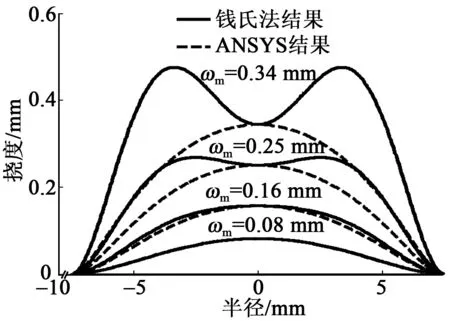
图2 不同中心挠度下薄片挠曲线对比

图3为施加在薄片上的压力和最大挠度关系的ANSYS仿真结果和“钱氏法”计算结果的对比。由图可看出，ANSYS结果和“钱氏法”的计算结果较符合，相对误差低于2.4%。

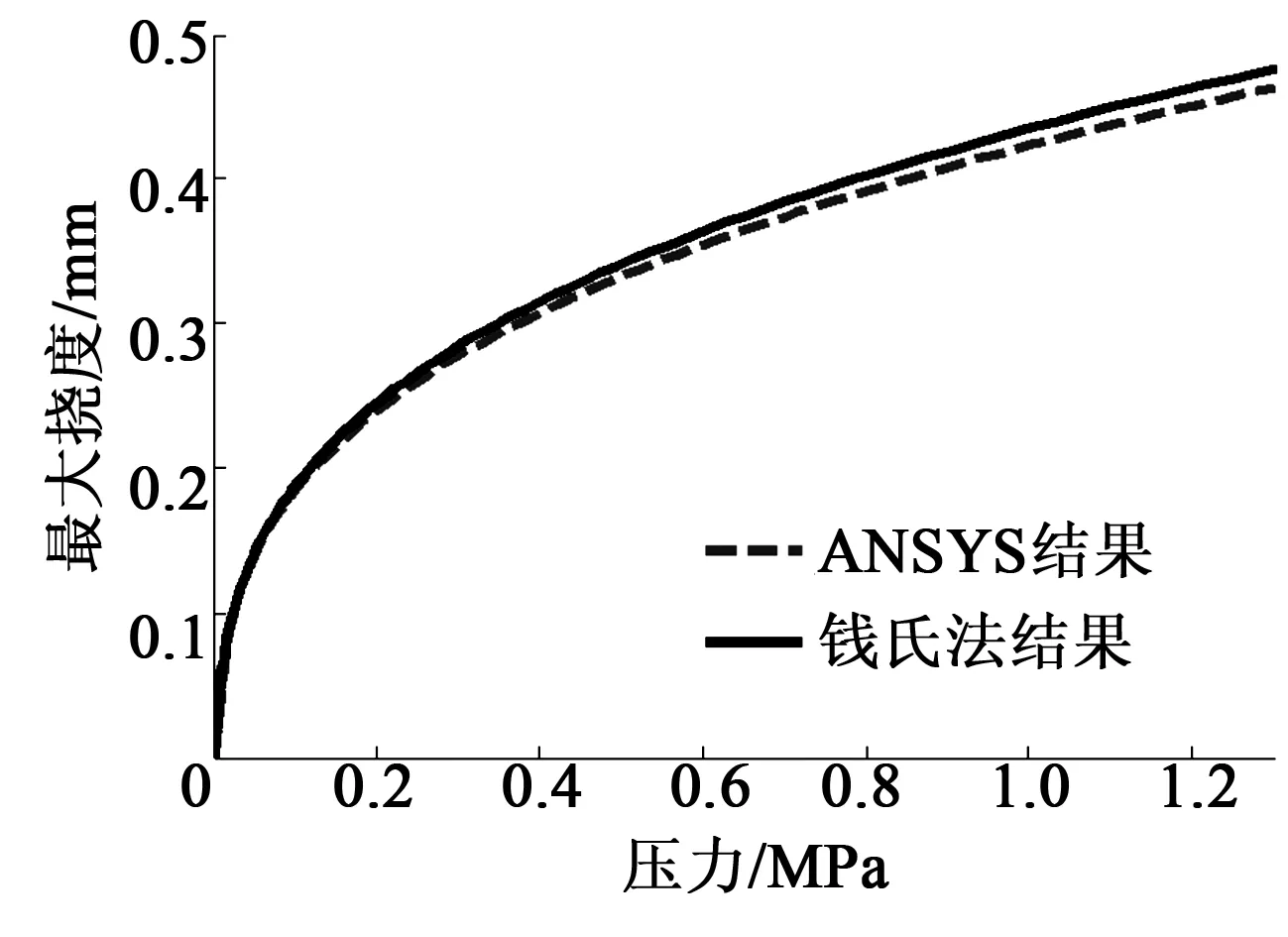
图3 压力最大挠度关系

由于“钱氏法”不能描述挠度较大时的挠曲线形状，在此利用S.Way级数展开法所得到的挠曲线解的形式[9]为

(3)

式中ai为各项的系数。

式(3)未描述最大挠度与挠曲线的关系，将最大挠度从式(3)中提取出来可得

(4)

通过ANSYS仿真可得不同最大挠度情况下的挠曲线形状，再辨识出各项系数bi，就可得挠曲线函数。在此利用式(4)前3项可得精度较好挠曲线函数式为

(5)

图4为不同最大挠度下的挠曲线形状。

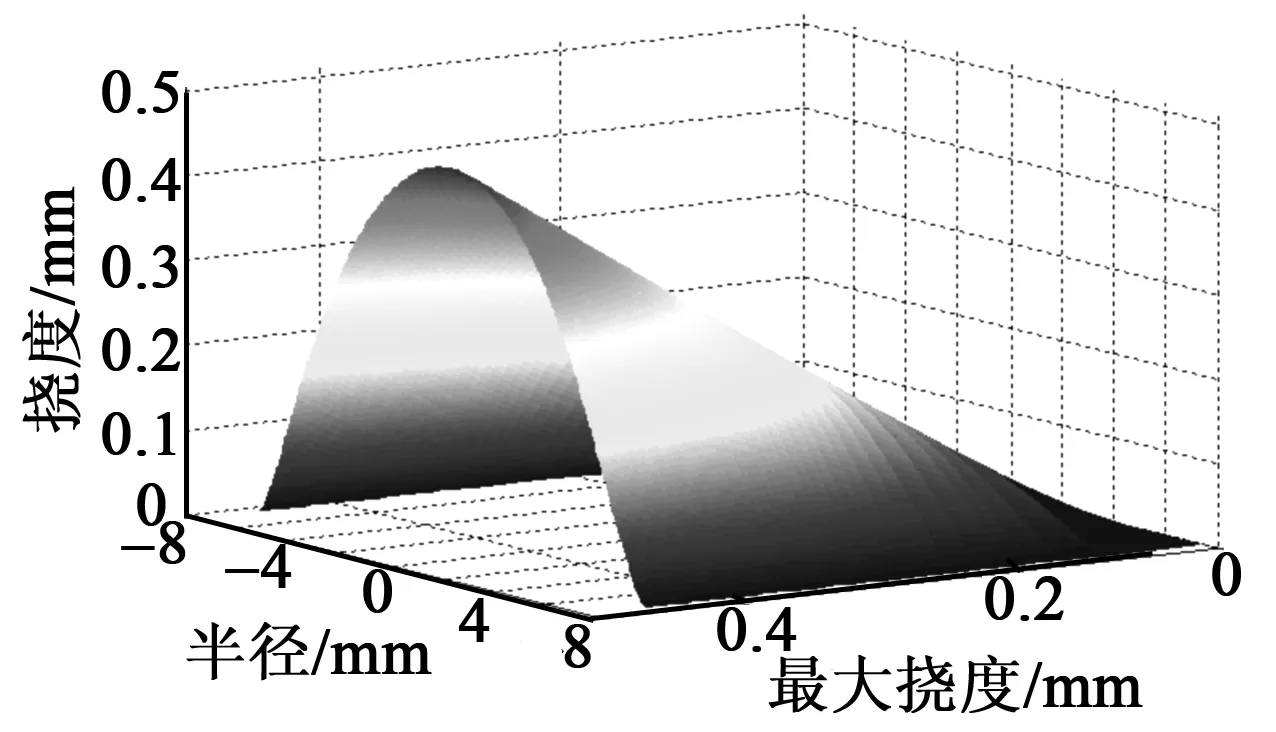
图4 最大挠度的挠曲线关系

综上所述，通过“钱氏法”可得压力-最大挠度的关系(见式(2))，利用S.Way的级数展开法所得挠曲线解可得不同最大挠度下的挠曲线形状函数(见式(5))。

2.2 位移放大器位移输入、输出关系推导

位移放大器中以液压油作为能量传递的媒介，由于输入位移较小，且考虑油液中混入气体对油液有效体积弹性模量的影响，将位移放大器中的油液视为可压缩流体。在压力p的作用下，位移放大器中有效体积弹性模量[11]为

(6)

式中：p0为大气压；a为含气量，是气体体积与油液总体积比；βo为纯油体积弹性模量；βe为有效体积弹性模量。

(7)

式中Vt为油液总体积。对式(7)两边同时积分可得压力由p0到p时位移放大器中油液体积的变化量ΔVt为

(8)

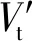
由式(5)所得挠曲线表达式ω(r)，对于位移放大器，若活塞动作位移为x，则位移放大器中油液体积变化ΔVt为

(9)

式中Ap为活塞面积。

由式(8)、(9)可得

Vt·(e[f(p0)-f(p)]-1)=8.06×10-5ωm-

Apx

(10)

联立式(2)、(10)可得到活塞位移x和薄片最大挠度ωm在一定的含气量下唯一的对应关系，至此得到了位移放大器输入-输出位移的关系。

图5为不同a下位移放大器输入-输出关系仿真曲线。由图可知，a对放大器性能的影响较大。因此，在建模的过程中需考虑a的影响。表1为计算和仿真的关键参数。表中，h为薄片厚度，E为薄片弹性模量，σ为薄片泊松比。

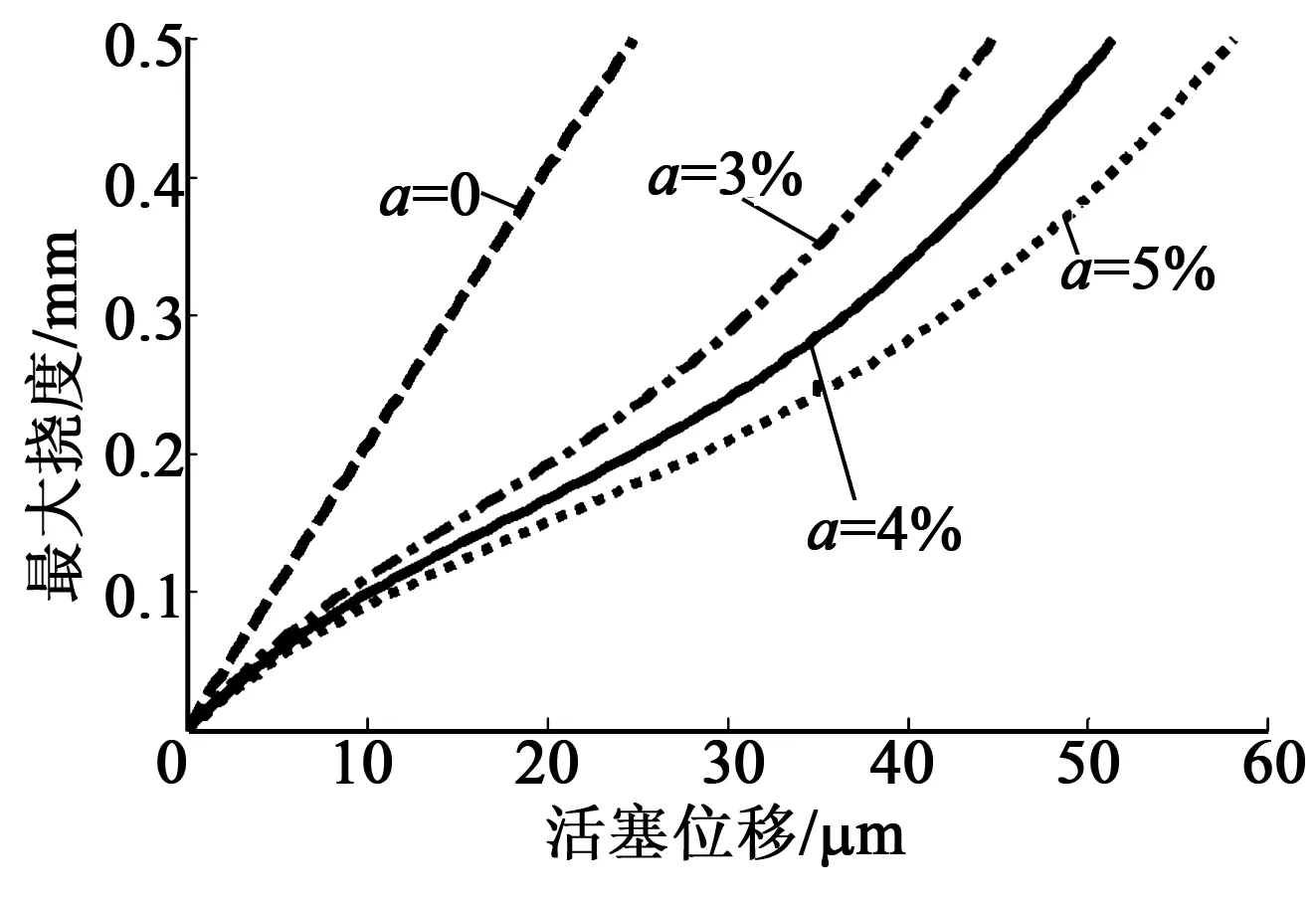
图5 不同含气量下位移放大器输入、输出关系

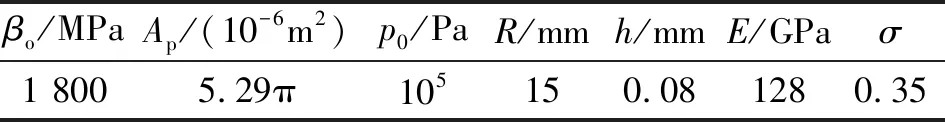
βo/MPaAp/(10-6m2)p0/PaR/mmh/mmE/GPaσ1 8005.29π105150.081280.35

3 位移放大器的动态模型

将位移放大器输入-输出位移近似表示为一个二阶线性系统,即

(11)

式中：ωn、ζ分别为描述活塞位移到位移放大器输出位移二阶线性系统的固有频率和阻尼比；F(x)为式(10)中所得活塞位移和薄片最大挠度的关系。

由于超磁致伸缩棒的响应时间远小于位移放大器的响应，故可以近似认为在实验中超磁致伸缩棒的输出位移相对于输入电流信号无滞后。位移放大器在幅值1.5 A和1.0 A的阶跃输入信号下的动态位移响应如图6所示。响应曲线的响应参数如表2所示。其中,MP为最大超调量，tP为峰值时间，可辨识出相应的ωn和ζ，取其平均值可得ζ=0.567 45，ωn=2 433 rad/s。

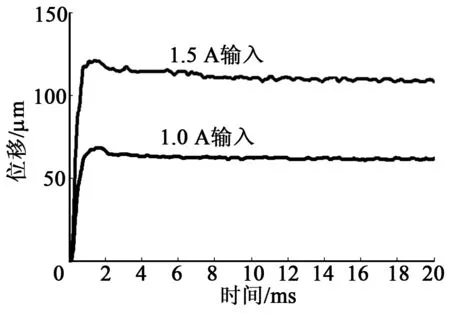
图6 阶跃响应曲线

电流/AMPtP/msζωn/(rad·s-1)1.50.112 21.520.571 42 518.51.00.117 31.620.563 52 347.5

4 输出特性实验研究

4.1 实验平台的搭建

图7为搭建的实验平台。信号发生器产生控制信号，功率放大器将控制信号放大驱动实验样机中的GMA，通过位移放大器将GMA输出位移放大，激光位移传感器采集GMA的输出位移和位移放大器的位移信号。

图7 位移放大器测试平台

4.2 位移放大器输出特性实验

图8为GMA在输入电流幅值0～6 A时，GMA输出位移和位移放大器输出位移的实验与理论数据。由图可知，当a=4%时，理论计算值和实验值较符合。当活塞位移为0～51.1 μm时，位移放大器的输出位移为0～470 μm，放大倍数大于9倍，理论与实验数据符合较好。

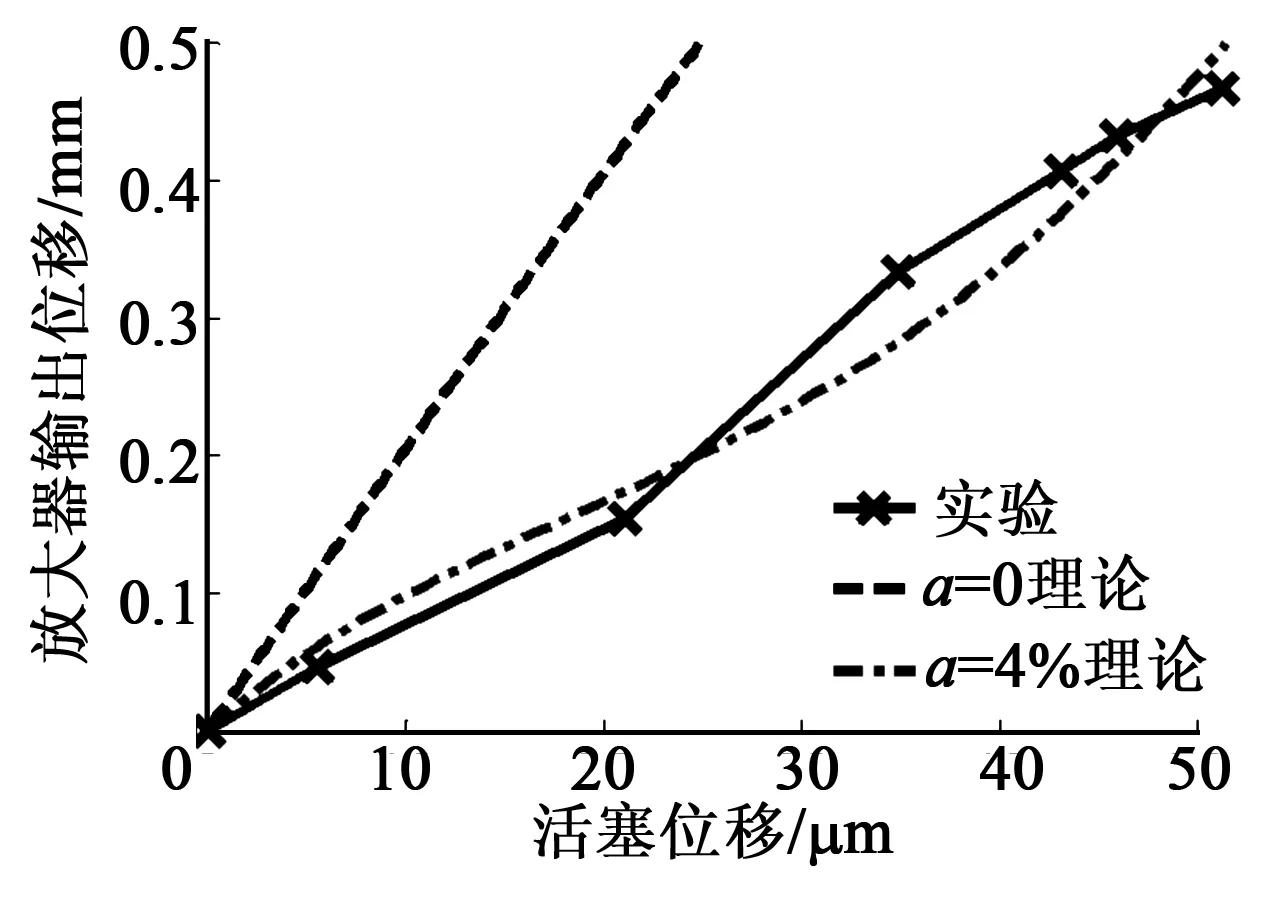
图8 位移放大器输入-输出关系曲线

图9为GMA在输入电流幅值4 A下的幅频特性曲线，即不同的输入信号频率对应位移放大器输出位移曲线。图中，点状曲线为放大器输入信号频率对应输出位移的实验曲线，水平实线为位移放大器输出最大位移幅值的0.707倍对应的值。由图可得，位移放大器输出位移随输入信号的频率增大而衰减，且该位移放大器的带宽约为150 Hz。

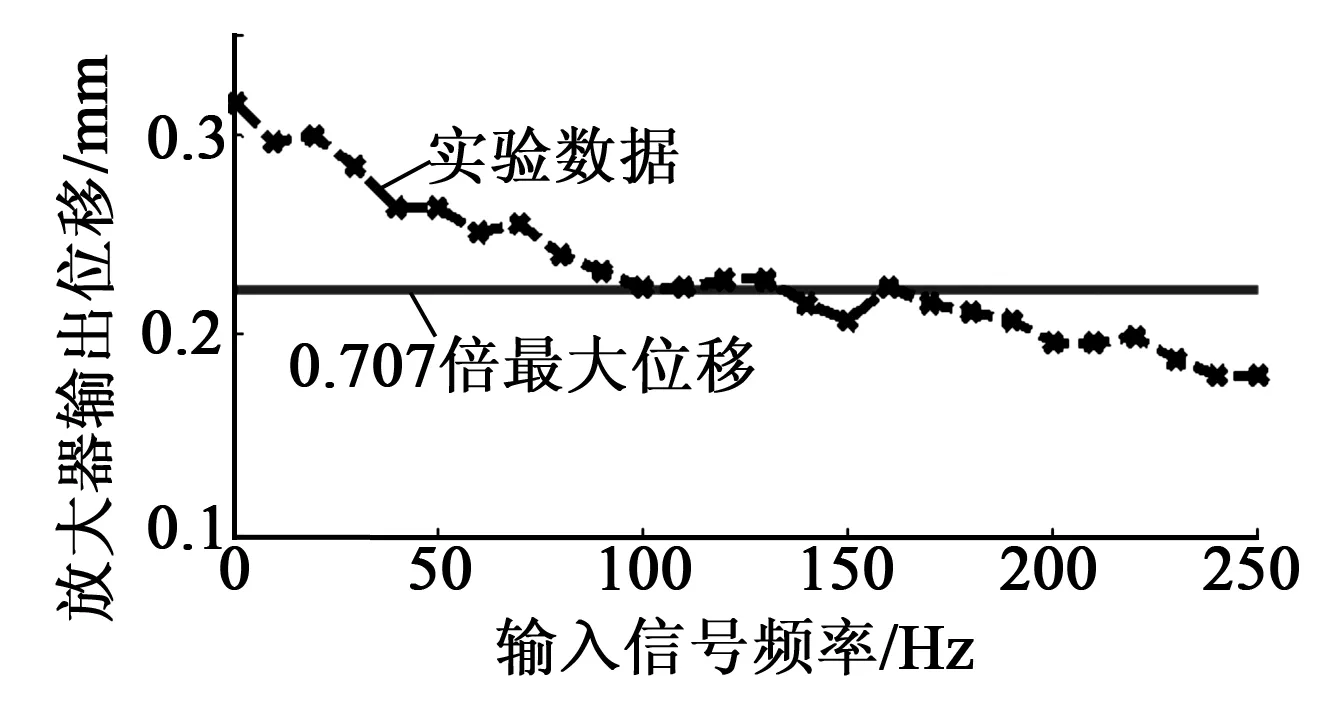
图9 放大器幅频特性曲线

5 结论

1) 利用“钱氏法”和S.Way解，建立了薄片大挠度变形模型，考虑油液有效体积弹性模量对位移放大器性能的影响，建立了位移放大器的位移输入、输出模型。

2) 在GMM执行器的输入电流为0～6 A时，测得活塞位移为0～51.1 μm，位移放大器的输出位移为0～0.47 mm，放大倍数可达9倍。

3) 通过实验分析了位移放大器的动态特性，通过实验辨识得到阻尼比为0.567 45，固有频率为2 433 rad/s，位移放大器的频宽约为150 Hz。