双压电叠堆驱动执行器率相关迟滞建模与分析
李宇阳,朱玉川,李仁强,王振宇,罗 樟
(南京航空航天大学 机电学院,江苏 南京 210016)
0 引言
压电叠堆执行器(PSA)利用压电陶瓷刚度大,输出力大,响应快和分辨率高等优点,已被广泛应用于光学、航空航天、电静液作动器、振动控制及医疗等技术领域[1]。但压电陶瓷输出位移小,且具有迟滞非线性,如压电叠堆的输出位移为0.1%~0.2%,导致其应用范围受限。因此,如何合理地将压电陶瓷的位移放大,使其可应用于更多场合成为一个亟待解决的问题。
针对智能材料驱动执行器输出位移小的缺陷,国内外学者提出了杠杆放大、菱形放大、压曲放大及柔性铰链等多种位移放大机构,虽然这几种放大机构都可实现执行器位移的成倍放大,但都存在一个共性问题,即随着输入信号频率的升高,输出位移幅值会出现较大幅度的衰减。蒋鑫[2]研制的压曲放大式磁致伸缩执行器样机,其动态频宽可达50 Hz;黄卫清等[3]研制了一种4根压电叠堆驱动的菱形放大机构,实验表明,在100 V的驱动电压下,10 Hz时输出位移约为18 μm,在100 Hz内,频率每升高10 Hz,输出位移将减小0.3 μm。研究者的研究范围多在100 Hz以内,未提供更多的位移-频率数据。然而,在电液伺服阀、航空航天作动器等领域均需具有高频响应特性的PSA[4]。
压电材料除输出位移小外,其固有迟滞特性也受到研究者们的广泛关注。近年来,国内外学者用Preisach模型、Bouc-Wen模型、Maxwell模型及神经网络等描述PSA的滞环。Goldfarb等[5]首先采用中心对称的Maxwell模型描述压电材料的迟滞特性,采用无质量、受摩擦力的物块-弹簧系统的输出力与输入位移的关系来描述迟滞现象。裘进浩等[6]在此基础上提出了一种非对称的Maxwell模型,将原模型基础单元拆分成一个上升段的基础单元和一个下降段的基础单元,使基础单元的力-位移曲线由原Maxwell模型对称的四边形变为梯形,具有描述非对称滞环的能力。
为实现压电叠堆执行器高频大位移和高精度控制,本文设计了一种双压电叠堆执行器(DPSA)。它由2个规格不同的压电叠堆同时驱动(复合驱动),2个压电叠堆间通过套筒连接,通过位移叠加方式实现位移的增大,并在600 Hz复合驱动时输出位移仅衰减了7.1%。同时,本文还对DPSA进行迟滞建模与仿真分析,运用系统动力学方程、准静态下的非对称Maxwell模型及一阶惯性环节等建立了DPSA的率相关模型,并将模型结果与实验结果进行了对比,在600 Hz内幅值最大误差不超过1.71 μm,均方根误差最大为1.34 μm。对比结果证明,本文所建立模型可较准确地描述执行器的迟滞非线性。
1 原理与结构
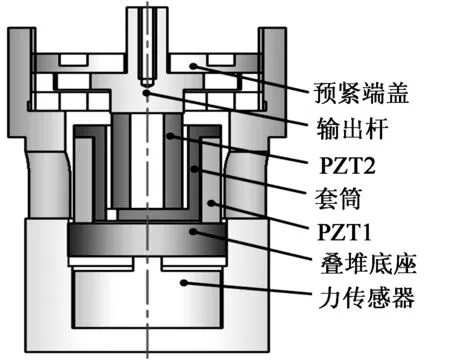
图1为DPSA原理图(以向上为正方向)。2个压电叠堆由一个套筒连接,筒形压电叠堆1(PZT1)伸长会同时带动套筒向正方向运动,套筒的运动会带动压电叠堆2(PZT2)向正方向运动,处于套筒内的PZT2在跟随套筒正向运动的同时自身也会伸长,从而PZT2顶端的输出位移是两叠堆位移的叠加,实现了在相同执行器长度下产生更大输出位移的效果。
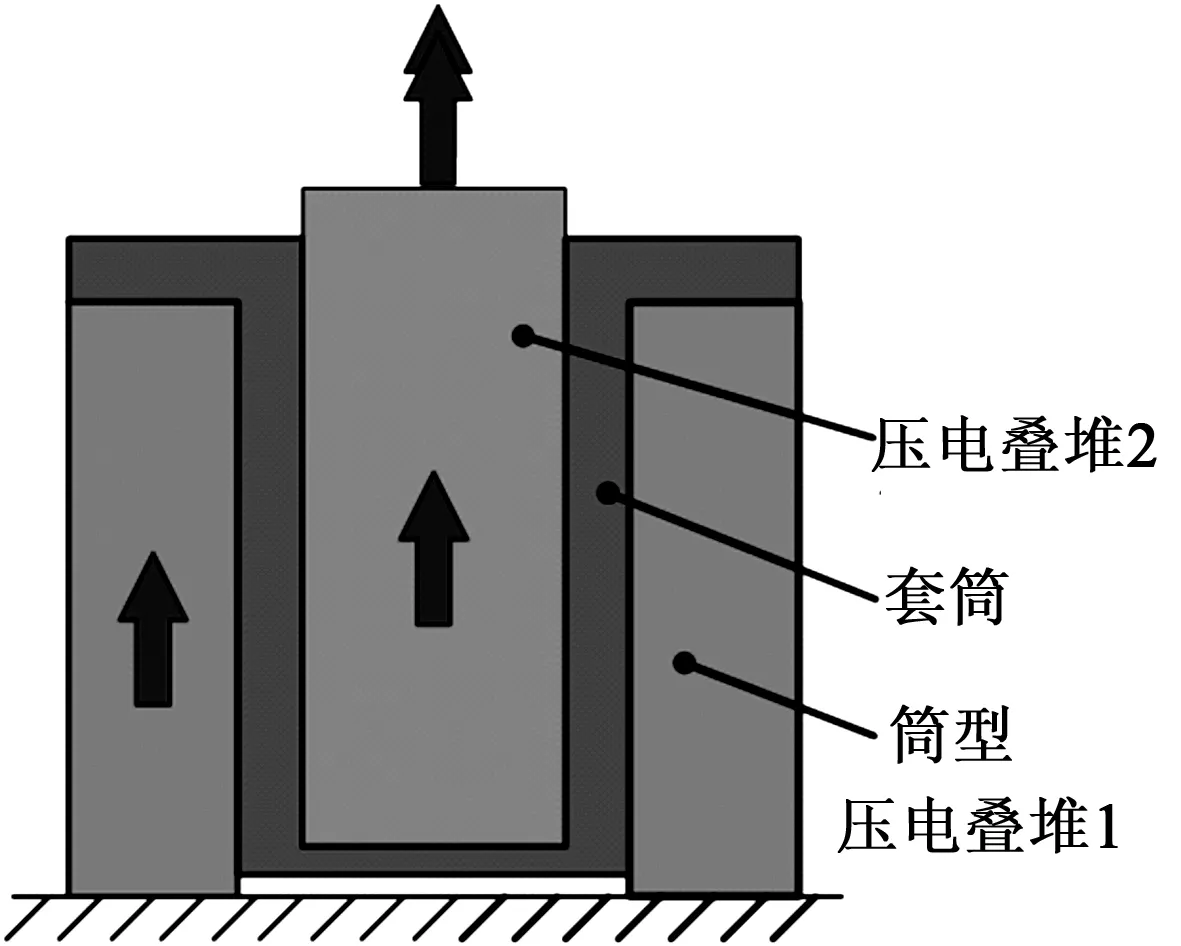
图1 DPSA原理图
根据现有的压电叠堆型号,考虑2个压电叠堆间的嵌套关系,DPSA结构如图2所示。其中,PZT1和PZT2是2个不同尺寸的环型压电叠堆(PZT1的型号为PTH1502619201,外径∅26 mm、内径∅19 mm、长度18 mm;PZT2的型号为PTH1501206201,外径∅12 mm、内径∅6 mm、长度20 mm)。由于PZT2需将导线引出以驱动,故在套筒底部开一个45°、宽度比导线稍宽的圆弧槽。
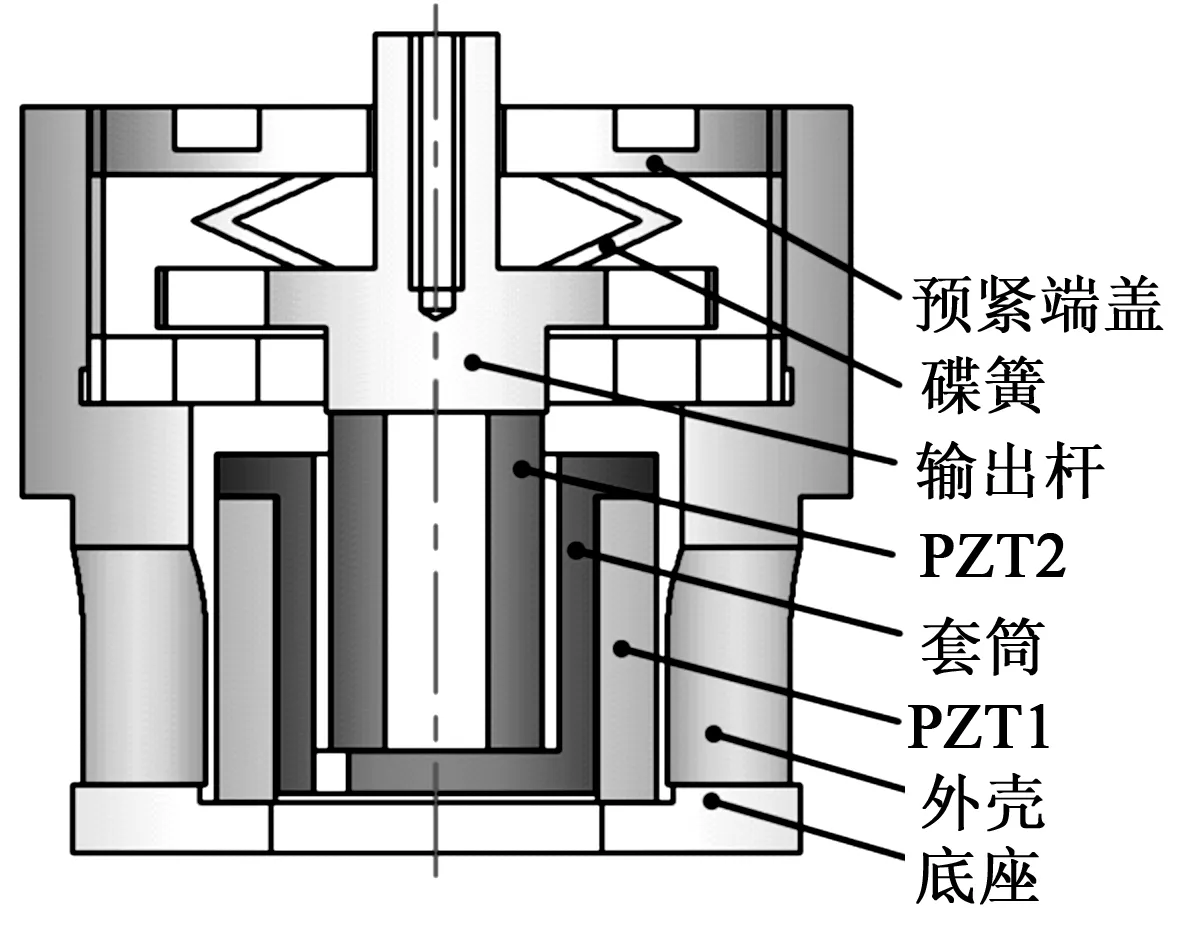
图2 DPSA结构示意图
在2个压电叠堆同时伸长时,传递到输出杆的伸长量是2个压电叠堆位移的叠加,碟簧同时为2个压电叠堆提供必要的预压力;2个压电叠堆同时缩短时,碟簧的回复力将输出杆压回,从而实现往复运动。此结构中,碟簧同时为2个压电叠堆提供相同大小的预压力,故碟簧的预压力应满足:
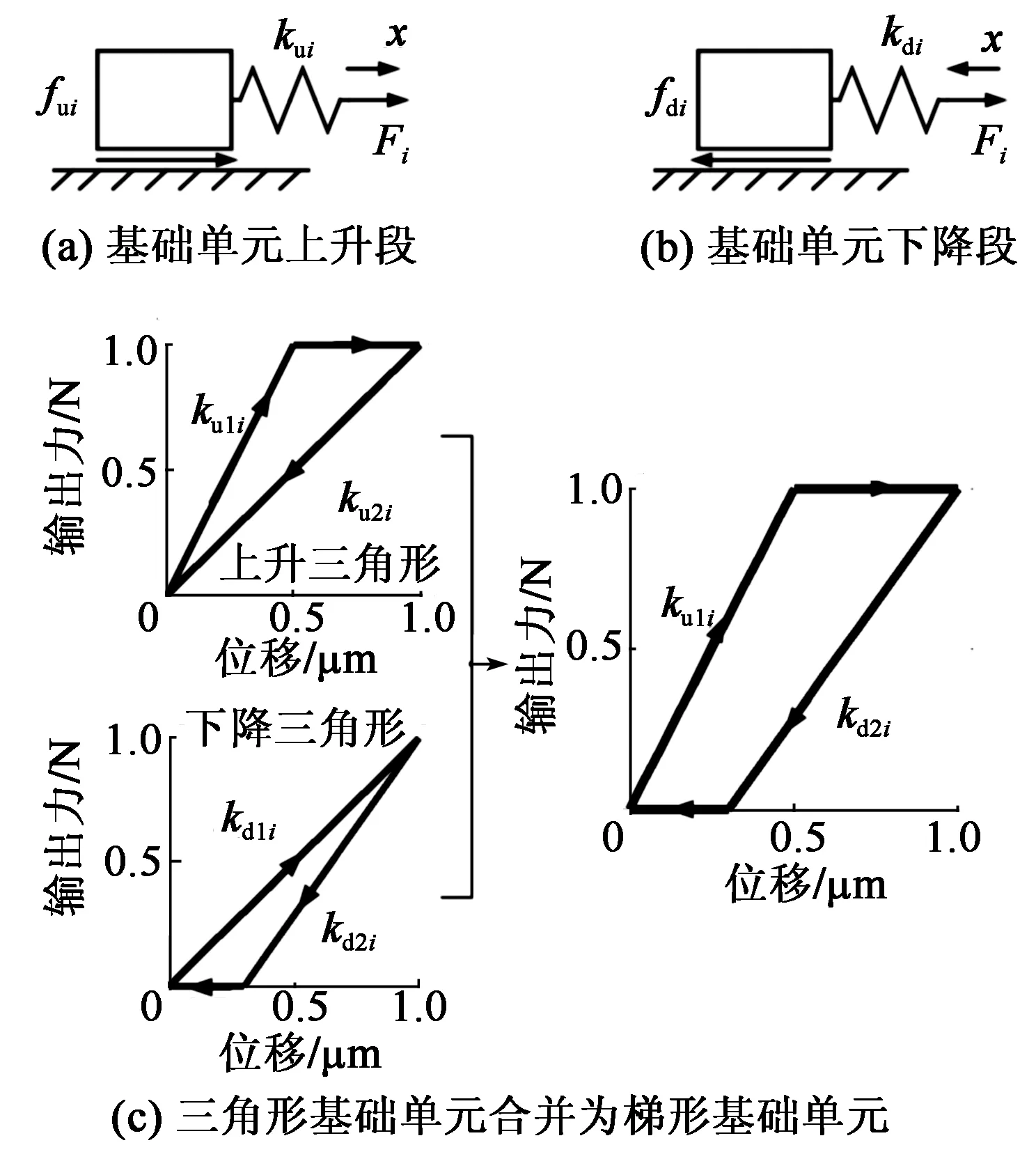
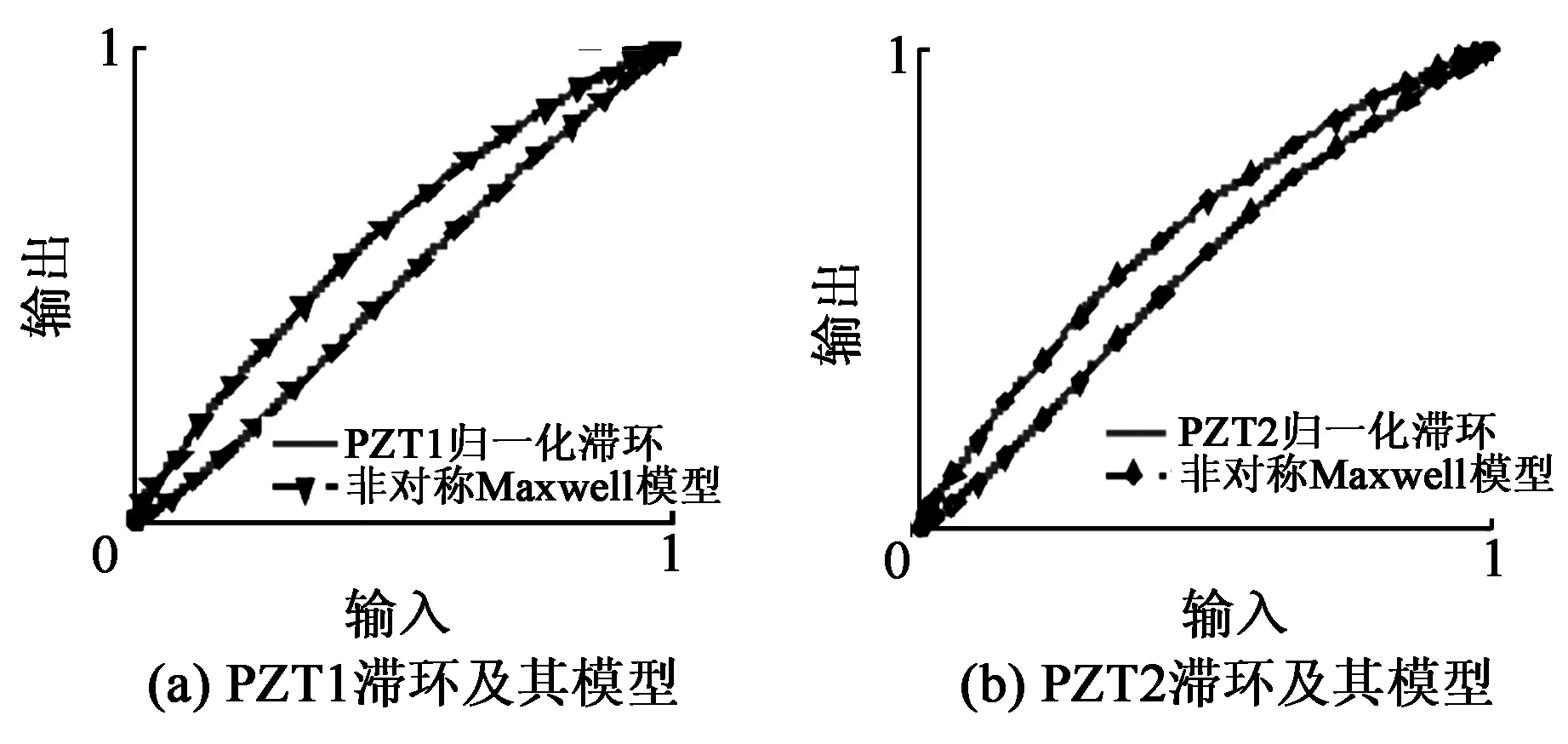
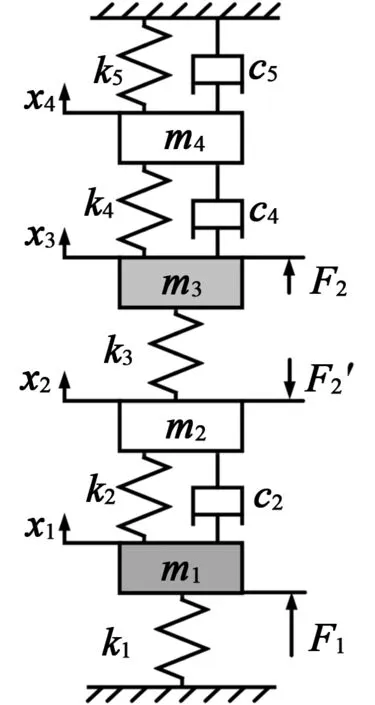
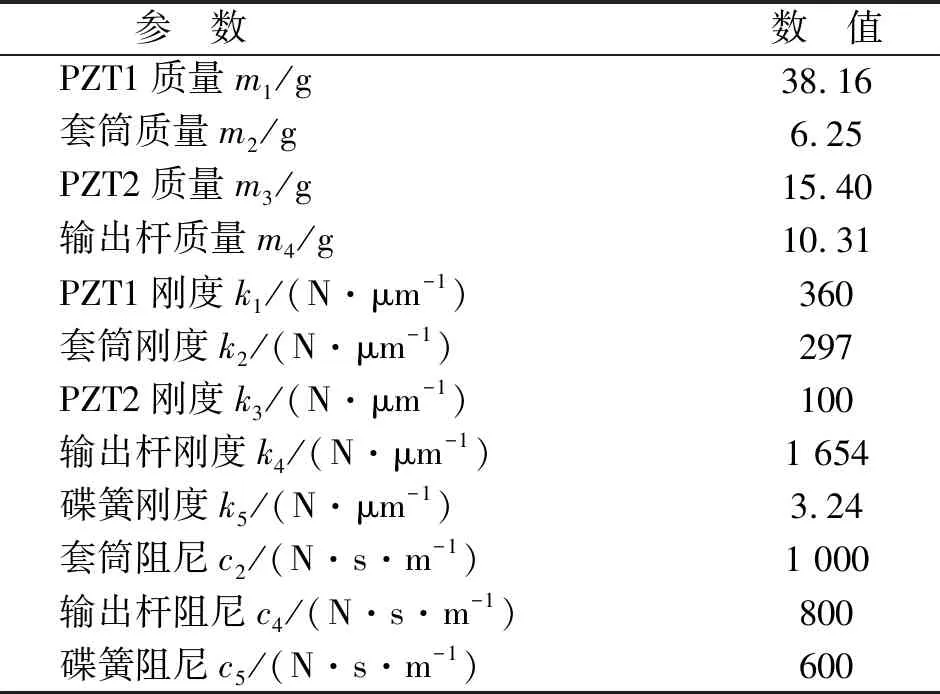
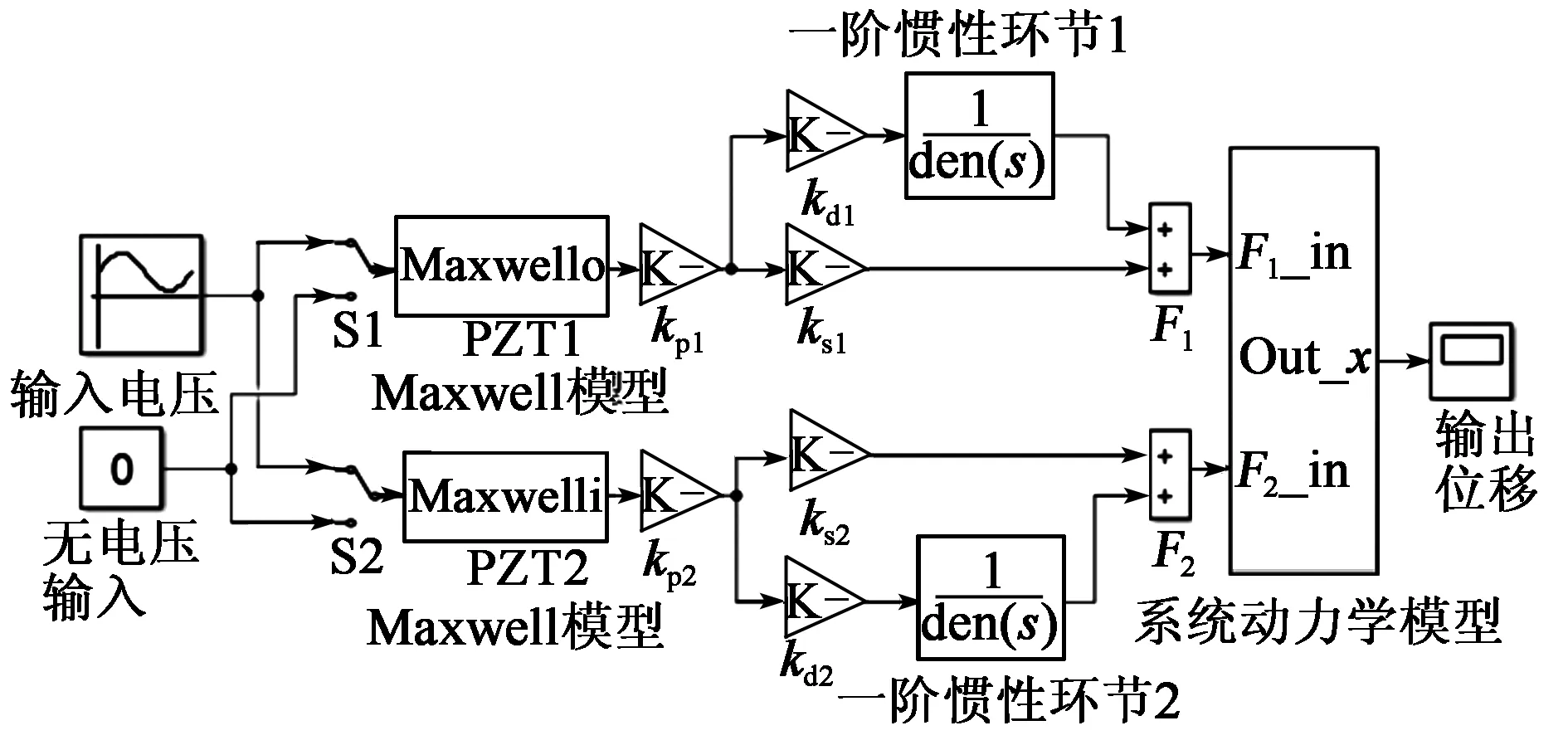
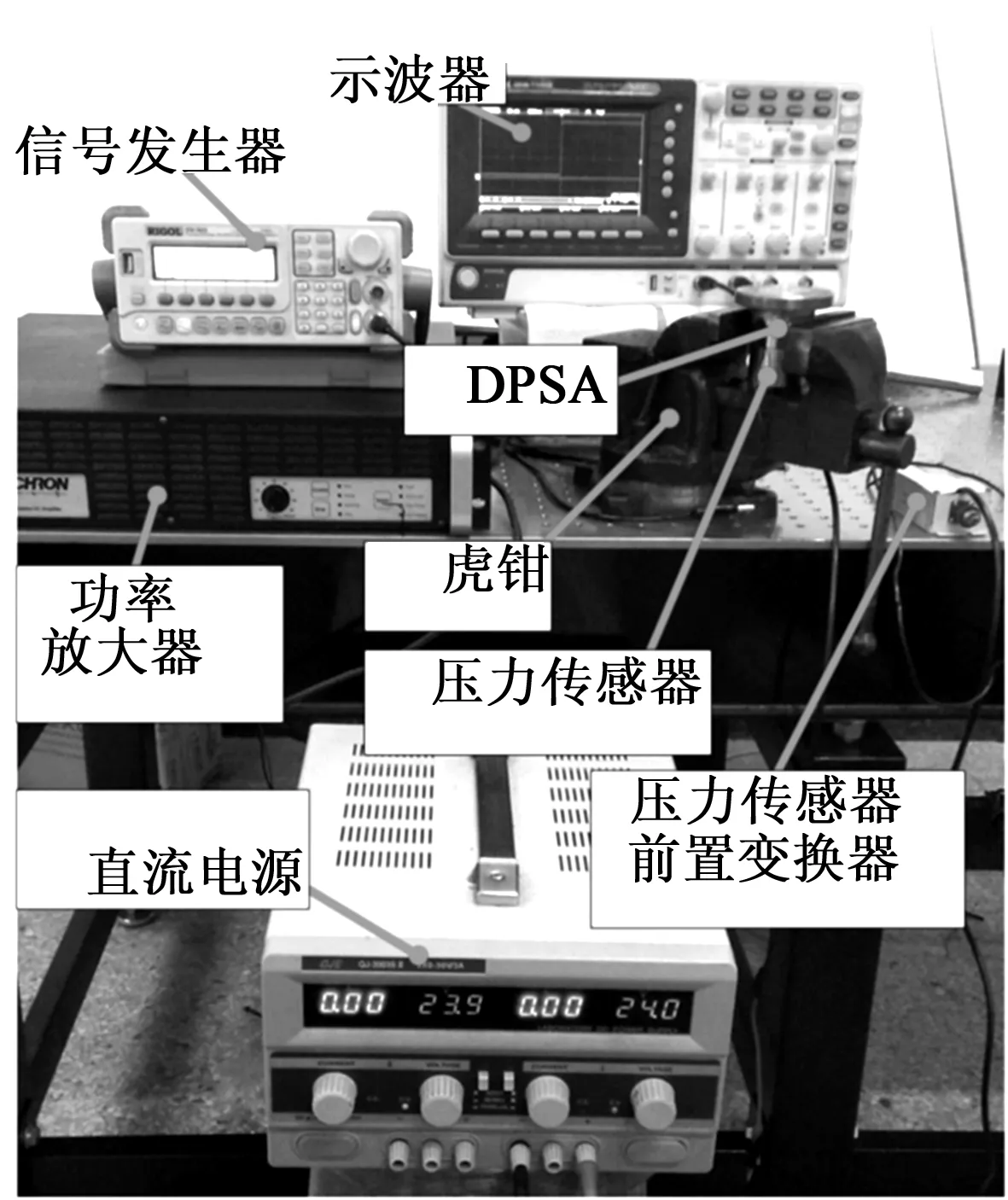
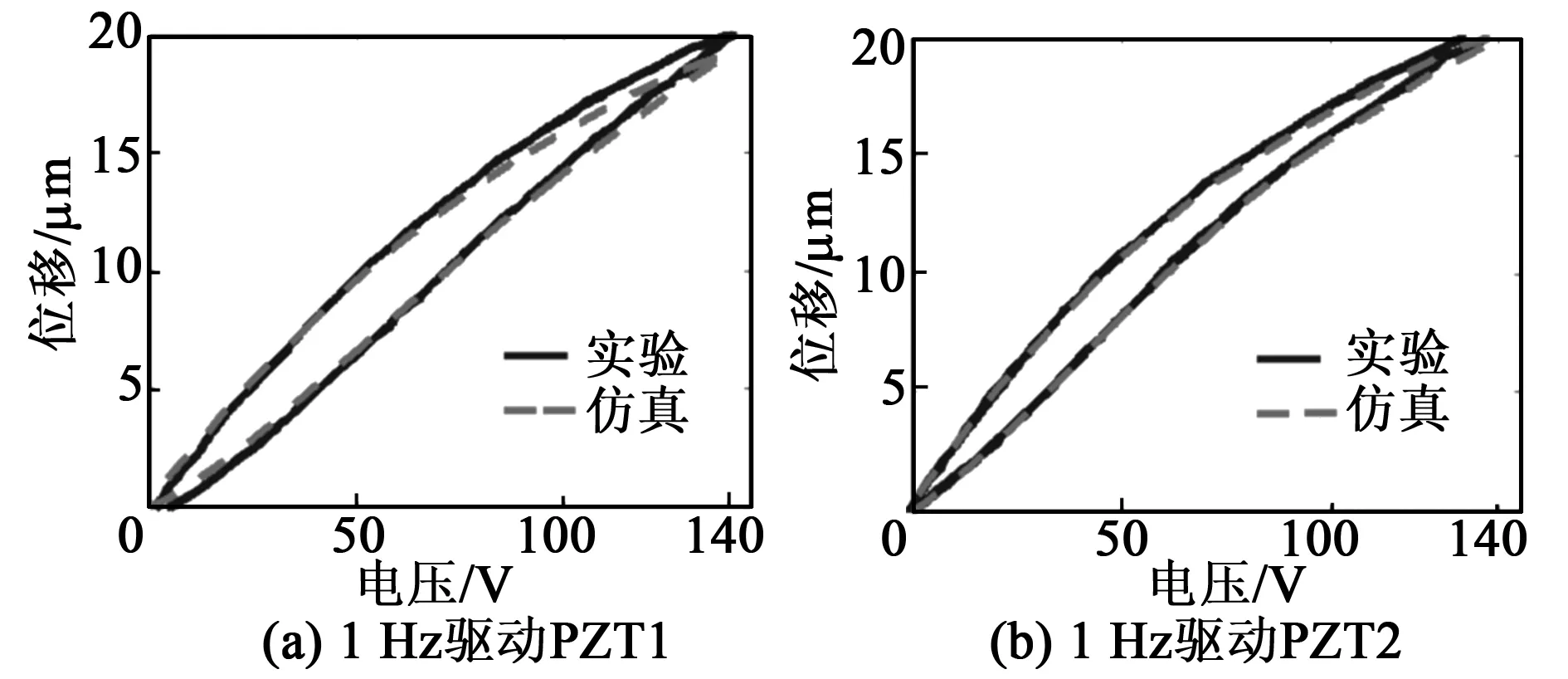
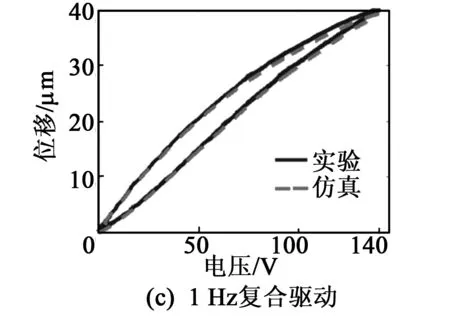
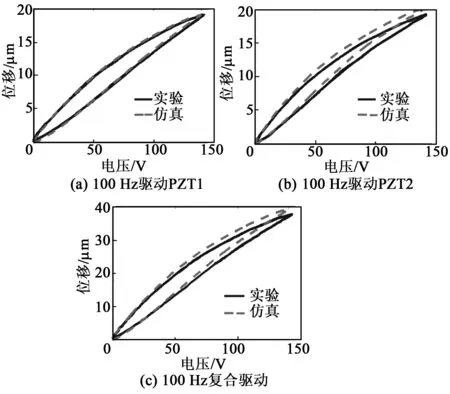
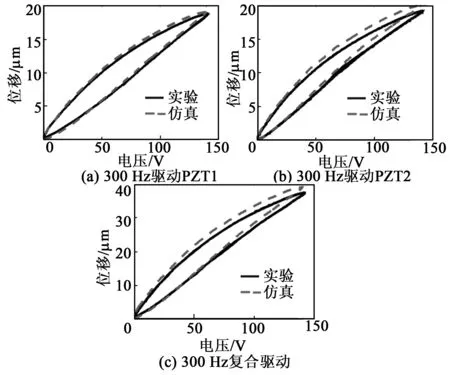
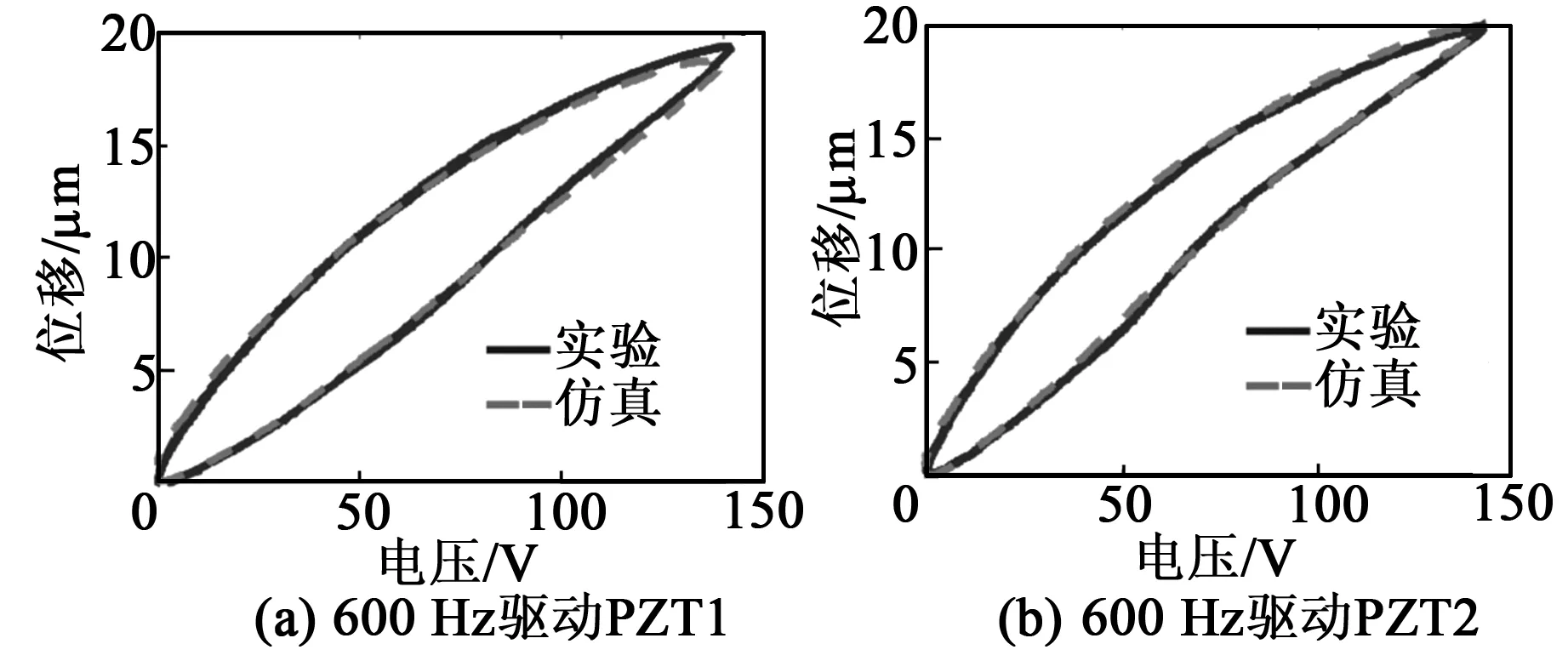
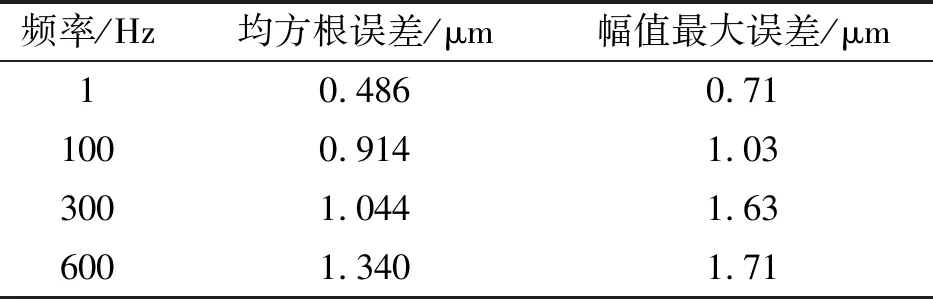
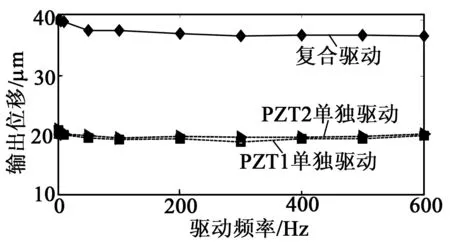
F预 (1) 式中:F预为碟簧提供的预压力;F预max1为PZT1所能承受的最大预压力;F预max2为PZT2所能承受的最大预压力。 为防止压电叠堆损坏,通过调整预紧端盖的旋合长度,使2个压电叠堆承受的初始预压力保持在500 N左右。 本文采用非对称Maxwell模型对DPSA进行准静态建模。非对称Maxwell模型由若干个梯形基础单元叠加而成,梯形可分解为上升段和下降段[6]2个基础单元,如图3(a)、(b)所示。上升段和下降段2个基础单元的输入与输出分别用2个有向的三角形单元进行数学描述,最终2个三角形单元可合并成梯形基础单元。 图3 非对称Maxwell模型基础单元 上升基础单元的输入(位移x)与输出(输出力Fu)的关系可表示为 (2) 下降基础单元的输入(位移x)与输出(输出力Fd)的关系可表示为 (3) 最终将各个单元模型并联叠加,得到系统模型表达式[6]为 (4) 式中:Fi(kT)为第i个单元当前输出力;Fi((k-1)T)为第i个单元前一个采样周期的输出力;fui,fdi,kui,kdi分别为第i个单元上升段摩擦力、下降段摩擦力、上升段弹簧弹性系数及下降段弹簧弹性系数;T为采样周期;Δx为输入位移增量。 非对称Maxwell模型实质是将单位化后的静态迟滞曲线的上升段与下降段各取n个点,斜率变化大的地方取点密集,斜率变化小的地方取点稀疏,通过第i点与第i-1个点之间的斜率与第i点的横、纵坐标,辨识出n个ku1i、kd2i与Δxi,从而将原静态迟滞曲线简化成多段斜率不同且首尾相连的有向线段,完成对迟滞曲线的描述。分别对DPSA中2个压电叠堆进行基于Maxwell模型的准静态参数辨识,首先要获得两叠堆各自的迟滞曲线。得到两叠堆各自的准静态迟滞曲线的方法为:在图2所示的DPSA中,用频率为1 Hz、峰-峰值140 V、偏置70 V的电压驱动PZT1,得到PZT1的电压-位移迟滞曲线;再用同样的电压信号驱动PZT2,得到PZT2的电压-位移迟滞曲线。在对两叠堆分别进行Maxwell准静态迟滞辨识的过程中,上升段和下降段均各取20个点。由于模型参数较多,本文仅对辨识结果进行对比。将PZT1、PZT2的归一化电压-位移迟滞曲线分别与辨识后的Maxwell模型的迟滞曲线进行对比,如图4所示。由图可知,Maxwell模型可精确描述执行器的滞环。 图4 Maxwell模型与实际滞环比较 在准静态时,压电叠堆的阻尼力和惯性力可忽略,在输入电压-力-位移的传递过程中,可认为压电叠堆的力-位移为线性关系,故电压-位移与电压-力的归一化迟滞曲线相同,因此,将Maxwell归一化迟滞模型作为压电叠堆准静态下的电压-力单位迟滞模型,用Fh1(t)和Fh2(t)表示。 (5) 图5 DPSA系统动力学模型 参 数数 值PZT1质量m1 /g38.16套筒质量m2/g6.25PZT2质量m3/g15.40输出杆质量m4/g10.31PZT1刚度k1/(N·μm-1)360套筒刚度k2/(N·μm-1)297PZT2刚度k3/(N·μm-1)100输出杆刚度k4/(N·μm-1)1 654碟簧刚度k5/(N·μm-1)3.24套筒阻尼c2/(N·s·m-1)1 000输出杆阻尼c4/(N·s·m-1)800碟簧阻尼c5/(N·s·m-1)600 压电叠堆各项参数由厂家提供,套筒与输出杆的参数由零件结构计算得到。由于PZT1为单端固定的压电叠堆,根据动能等效原理[8],其等效质量为m1/3,在仿真中PZT1用其等效质量搭建模型。 引入动力学方程描述DPSA系统的动态响应,但动力学方程并不包含压电叠堆自身输出力的动态响应。为了描述压电叠堆输出力的动态响应,将压电叠堆的力响应分为静态力响应与动态力响应,最终压电叠堆输出力的形式为二者按比例进行叠加,即 (6) 式中:j为压电叠堆的序号(j=1,2),分别表示PZT1与PZT2;Fj(t)为式(5)中F1与F2等同;Fsj(t)为PZTj的静态力响应;ksj为PZTj静态力比例系数;Fdj(t)为PZTj输出的动态力响应;kdj为PZTj动态力比例系数。 PZTj的动态力可视为一阶惯性环节[9],Fsj与Fdj分别为 (7) 式中:kpj为PZTj的单位力放大倍数,在数值上等于压电叠堆的阻断力;τj为PZTj的一阶惯性环节时间常数,其值可由压电叠堆阶跃响应实验得出;Fhj(t)为归一化处理后的Maxwell模型描述的准静态单位力滞环。 在输入电压频率很低时,系统可视为准静态系统,τj的影响可忽略,则在输入电压频率很低时可化简为 Fj(t) =(ksj+kdj)·kpj·Fhj(t) = kpj·Fhj(t) (8) 联立式(5)~(8),当输入电压频率很低时,DPSA的电压-位移迟滞曲线由Maxwell模型与系统动力学方程决定;当输入电压频率高时,DPSA电压-位移迟滞曲线由Maxwell模型、系统动力学方程和两压电叠堆的一阶惯性环节共同决定,从理论上说明了该模型可描述DPSA的静态迟滞特性和动态迟滞特性。 利用上述理论,在Matlab/Simulink中建立的仿真模型如图6所示。在模型中通过控制开关S1与S2的开闭可模拟PZT1、PZT2单独驱动及复合驱动的状态。 图6 DPSA系统Simulink模型 PZTj一阶惯性环节的单位力比例系数kpj在数值上等于压电叠堆的阻断力,由厂家提供的参数可知,PZT1和PZT2阻断力分别为7 200 N和3 000 N,故kp1=7 200,kp2=3 000。 由于τj为压电叠堆自身的性质,需去除压电叠堆外的其他零件进行阶跃响应实验,但叠堆工作时需要一定的预压力,因此,在辨识τj的实验中移除碟簧,将输出杆用上端盖压紧,下方用称重力传感器测量力响应,如图7所示。 图7 力响应测试结构图 在此结构下进行了140 V阶跃电压下PZT1单独驱动及PZT2单独驱动实验,力响应辨识实验测试平台如图8所示。信号发生器输出的阶跃信号经功率放大器放大后输入PZTj,叠堆产生的力会由底部的压力传感器采集、转化为电压信号,并输入示波器进行显示。直流电源用来为压力传感器供电。 图8 力响应实验测试 平台一阶惯性环节的阶跃响应[10]为 (9) 式中:Fj(t)为PZTj的阶跃力;Fmaxj为PZTj阶跃响应恒定后的力。 实验中,由于称重传感器存在底噪,且所测得的阶跃力为毫伏级,所用称重传感器的灵敏度为600 N/V,故所得结果存在较大噪声。为消除噪声影响,在Matlab中借助Curve Fitting Tool工具对测得的阶跃力响应曲线用式(9)拟合,得到在140 V电压下PZT1、PZT2单独驱动的阶跃力响应曲线,如图9所示,由式(9)可得τ1=138.5 μs,τ2=120.9 μs。 图10为双压电叠堆执行器实物及其位移测试平台。信号发生器输出的正弦电压经功率放大器放大后输入PZT1与PZT2,使DPSA输出杆产生位移,此位移由电涡流采集后转换为电压信号在示波器上显示。 图10 双压电叠堆执行器实物及其位移测试平台 将得到的实验数据与仿真作对比,以验证仿真模型的准确性。在峰-峰值140 V、偏置70 V的电压、碟簧预压力500 N的条件下,对PZT1单独驱动、PZT2单独驱动、复合驱动3种情况的滞环进行对比,结果如图11~14所示。复合驱动下模型检验误差如表2所示。 图11 1 Hz驱动DPSA电压-位移滞环仿真与实验对比 图12 100 Hz驱动DPSA电压-位移滞环仿真与实验对比 图13 300 Hz驱动DPSA电压-位移滞环仿真与实验对比 图14 600 Hz驱动DPSA电压-位移滞环仿真与实验对比 频率/Hz均方根误差/μm幅值最大误差/μm10.4860.711000.9141.033001.0441.636001.3401.71 由图11~14及表2可知,建立的模型可较好地描述PZT1单独驱动的迟滞曲线,对于PZT2单独驱动及复合驱动的情况,此模型在准静态下可准确描述执行器滞环,在动态时可描述滞环变化趋势。600 Hz内,复合驱动下幅值最大误差不超过1.71 μm,均方根误差最大为1.34 μm,随着频率的增加,模型误差有增大趋势。在准静态时幅值存在误差的可能原因是压电叠堆实际的阻断力与厂家提供的阻断力有微小差别,且每次实验时功率放大器的放大倍数可能存在微小波动。综上所述,此模型描述DPSA动态特性的可行性得到验证。 PZT1、PZT2单独驱动及复合驱动的位移随频率的关系如图15所示。由位移-频率曲线可知,到600 Hz为止,DPSA在3种驱动模式下的位移衰减均未达-3 dB,复合驱动时在600 Hz衰减7.1%,与其他位移放大机构相比,响应频率有很大提升,与同等长度的压电叠堆执行器相比,输出位移可达2倍。 图15 不同驱动形式下DPSA位移-频率的关系 本文提出并设计了一种双压电叠堆复合驱动的执行器,包含2根尺寸不同的压电叠堆,可单独驱动,也可同时驱动。利用非对称Maxwell模型建立在静态下2个压电叠堆的电压-力单位迟滞曲线,并通过一阶惯性环节描述压电叠堆的动态迟滞曲线,将合成后的力输入系统动力学模型。通过仿真与实验的位移对比,600 Hz内复合驱动的幅值最大误差不超过1.71 μm,均方根误差最大为1.34 μm,说明Simulink模型可描述滞环变化趋势,且有一定的预测性。执行器在600 Hz内,位移衰减了7.1%,与其他位移放大机构相比,其具有很好的高频性能。本文从原理上验证了双压电叠堆作动器实现位移叠加的可行性,若需要得到更大的叠加位移,可采用更长且可互相匹配的压电叠堆进行实验研究。2 率相关迟滞非线性模型及参数辨识
2.1 非对称Maxwell准静态模型
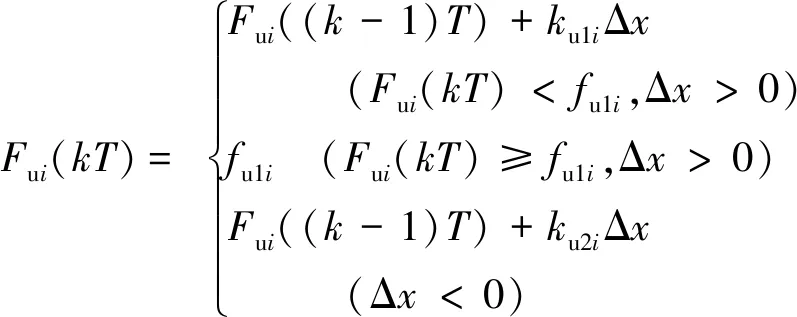
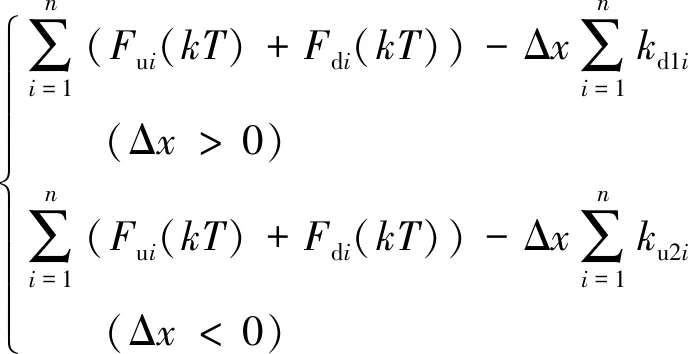
2.2 率相关迟滞模型的建立
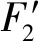
2.3 迟滞模型参数辨识
3 执行器仿真与实验对比


4 结束语

