把握问题本质 立足数学建模 生成解法多样——抛物线中三角形面积最值的解法探究

江苏省南京市金陵中学西善分校 (邮编：210041)

1 试题呈现

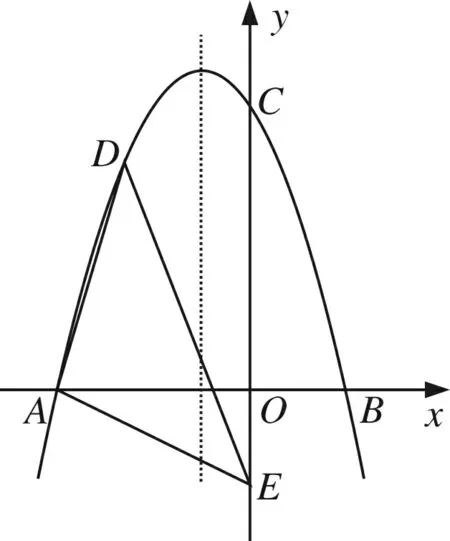
图1

(2018年山东泰安第24题)如图1，在平面直角坐标系中，y=ax2+bx+c交x轴于点A(-4，0)、B(2，0)，交y轴于点C(0，6)，在y轴上有一点E(0，-2)，连接AE．

(1)求二次函数的表达式；

(2)若点D为抛物线在x轴负半轴上方的一个动点，求△ADE面积的最大值；

(3)抛物线对称轴上是否存在点P，使△ABC为等腰三角形，若存在，请直接写出所有点P的坐标，若不存在，请说明理由．

2 特点解读

2.1 背景熟悉，层次清晰，考查真功

全国各地的中考试卷中，以二次函数图象为背景的考题屡见不鲜，是中考的重点话题之一．本题以二次函数为背景，借助平面直角坐标系和坐标，将抛物线和几何图形有机结合起来，实现了“以数解形、以形助数”的目的．不仅考查“数与代数”和“图形与几何”的核心知识，同时也蕴含着数形结合、分类讨论、特殊到一般等数学思想，其计算部分的方法也为以后的解析几何奠定了基础．

本题已知与坐标轴的交点A、B、C，求函数表达式．方法不唯一，可设一般式也可设交点式，是基于学生的理解考查基本功．问题2中，抛物线内嵌了一个三角形，另一个定点却在y轴上，探究动点问题的三角形面积最值，整个配图一条抛物线和一个三角形，问题清晰明了，图形也简洁清爽．本题的设置由易到难，梯度分明，不管是求表达式，还是探究面积最值，或是等腰三角形的分类讨论，都是数学中的基本问题，每个层次学生均能有所收获．在熟悉的背景下，考查了学生的基础知识、基本计算、基本问题解决等数学基本功．

2.2 注重理解，立足建模，解法多样

笔者结合近几年各地中考试题，发现与本题素材类似的试题较多，二次函数的图象综合题或多或少都有“最值”的影子，仔细研究，不难发现此类题有个共同的特点．题目入口很宽，思路灵活，既涵盖了抛物线和三角形的综合知识，又突出了对问题本质和思维能力的考查．试题还立足于数学建模，不同视角下的建模就能生成不同的解法，有偏重于计算，有偏重于理解的，有偏重于转化的，形式多样，精彩万千，兼顾到了不同层次、不同思维、不同能力下各类学生的数学理解，具有很高的信度和效度．

史宁中教授认为，最基本的数学思想有三种，抽象、推理和模型．本题不管是哪种方法求面积最值，最终的核心都要回到建立模型上，用建模来统领所有解法具有很好的指导价值．因此，此类题作为中考的优质素材，不仅实现了一题多解到多解归一的升华，同时也提升了学生的思维空间．

3 解法赏析

本题3个小问的解法均不唯一，限于篇幅，这里只探究第(2)问的解法．

抛物线中动点三角形面积最值问题解决方法通常可分为两大类：一是运用“代数解析”的方法，将面积建立二次函数模型，利用二次函数最值解决；二是运用“构图分析”的方法，建立几何模型，从运动的角度分析出最值位置，求出此位置的面积即可．

3.1 代数解析，建立函数模型

(1)思路：运用填补，化不规则图形为规则图形

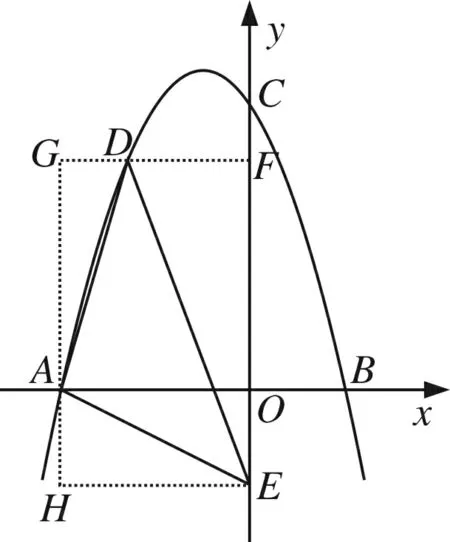
图2

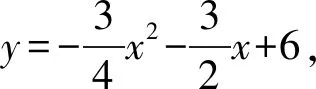
评析当三角形的三边都不与x轴或y轴平行时，填补成规则图形，这种面积的间接算法是求面积的常见思路．此思路下，还可以填补转化为直角梯形等多种规则图形，计算原理都是一样．

(2)思路：借助平行，构造相似，直接求高

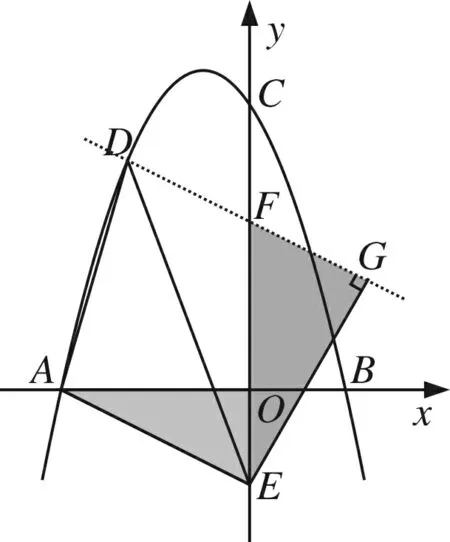
图3

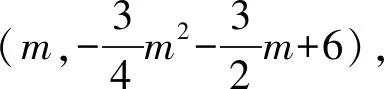
评析底边长度已知的情况下，用直接求高来表示面积也未尝不可．在平面直角坐标系中，垂直线段的长度基本都可通过构造相似求解，这也是坐标系中研究几何图形的常用方法之一．

(3)思路：借助平行，改变形状，转化面积

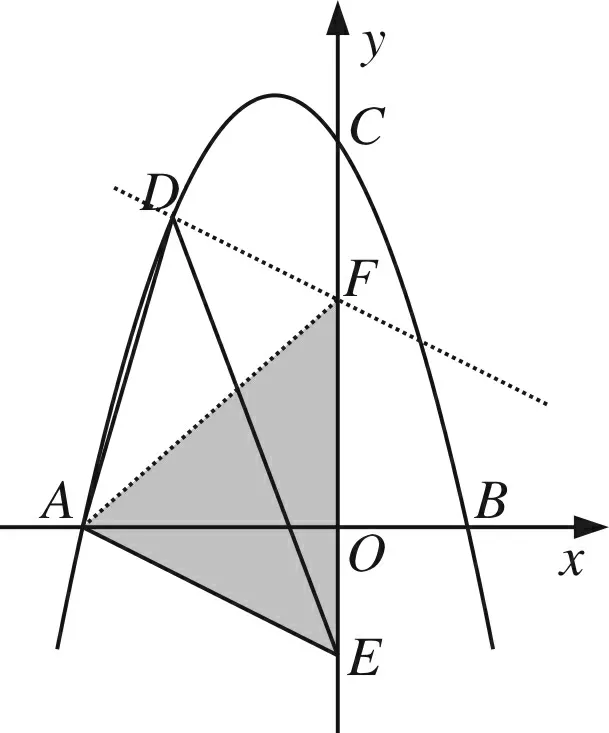
图4

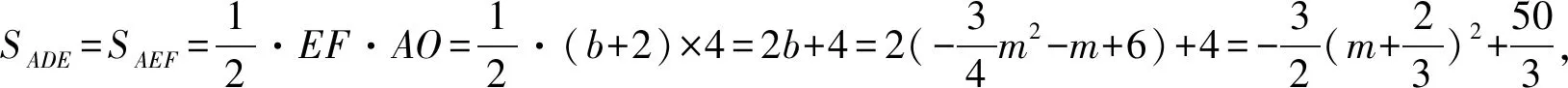
评析平行线可以利用同底等高在面积不变的前提下改变三角形的形状，从而可以达到改“斜”归“正”的目的，是“转化思想”的一种体现．

(4)思路：运用切割，左右整合，宽高求积

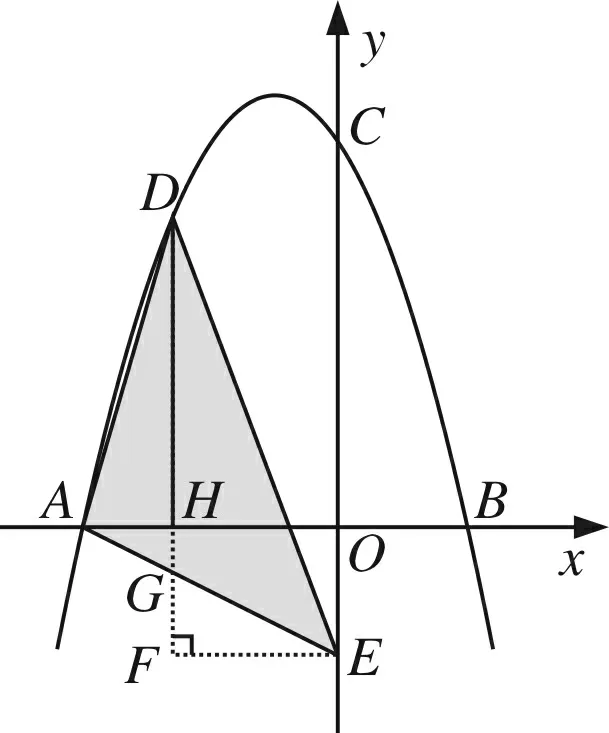
图5

评析平面直角坐标系中任意三角形按左右分割，再整合左右就能推出宽高公式，面积等于水平宽与铅直高乘积的一半．在理解原理的情况下，此法能帮助学生更加便捷地计算面积，是笔者认为值得推广的方法之一．

3.2 构图分析，建立几何模型

(1)思路：平移视角，相切位置，面积最大

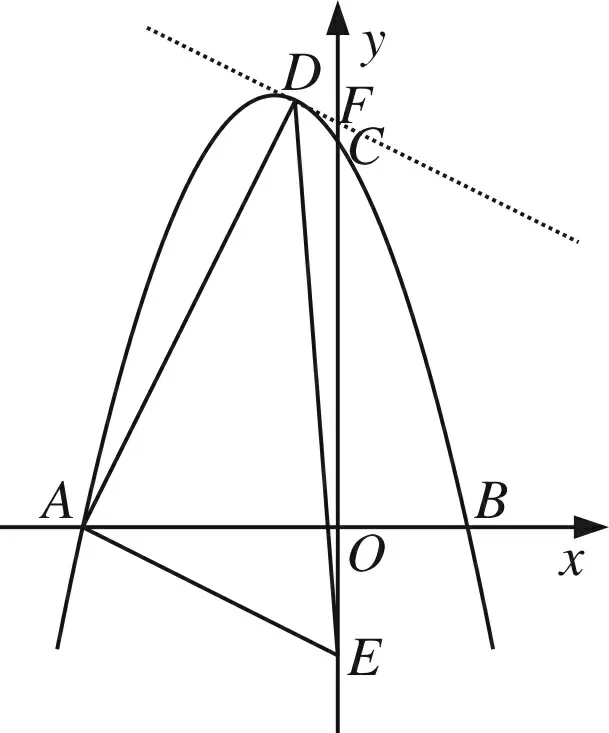
图6

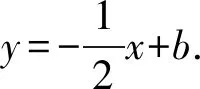
评析借助平移，换个视角动态分析，找“形”上的临界位置，转化为“数”上的关系解决．这种“以形助数，以数解形”的思想，是数学思维和能力的更高体现．

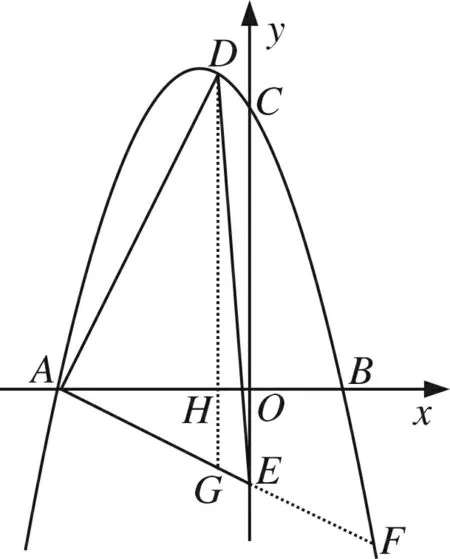
图7

(2)思路：分析规律，中点位置，面积最大

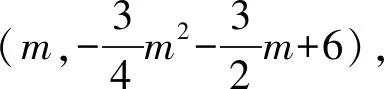
评析在理解面积为二次函数的前提下，通过图象的对称性，推理出最值的位置．此法对于学生的观察力和分析推理的能力要求很高，而且关于“中间位置为最值”的认识，也可以用代数解析的方法证明这个结论，当动点横坐标等于与抛物线两交点的中点横坐标时，面积最大．

4 教学导向

4.1 关注学生思维差异，从“一题一解”到“一题多解”

解题活动是数学教学最基本的活动形式，学会解题是学好数学的关键. 笔者认为解题教学不能以一解论之，因为学生的思维不同，有的偏重于代数的计算，有的偏重于图形的分析，有的偏重于问题的推理，而一道好题的解法应当会兼顾到各类层次的学生，会关注到各种思维的差异，因此教师要让每位学生都学有所获，得到发展，就必须关注学生的差异，立足于学生的思维来教解题．

基于学生不同视角下对问题的理解，不同想法就可以诞生出不同的解法，只要解法思路合理，可鼓励学生大胆尝试. 这样一来，一道“一题多解”的题，它的价值就能得以体现，它的立意也不再局限于“一道”，不但充分挖掘了知识方法间的联系，而且还能从多解中提升学生的思维，激发数学的兴趣．

4.2 提炼解题思想方法，从“一题多解”到“多解归一”

研究一道中考好题，整理不同思维下的解法，实际上是一个学教解题的过程．学生的解法可以是单向，但教师的认识必须是多维的．一题多解并不是为了炫技能，它恰恰反映的是教师对试题研究是否充分和对背后知识理解是否透彻，归根到底考验的是教师解题教学的基本功．笔者认为教师的解题教学必须先从研究试题开始，因为只有打开思路，研究多种视角多种解法，教师才有可能站在更高的高度，比较解法之间的差异，关注解法之间的联系，提炼出更好的解题思想来统领所有解法，即“多解归一”．这样教给学生的解法，才是完整的，是有高度的，是真正蕴含“数学思想”的方法．

知识是永远学不完的，题目也是永远做不完的，题只是知识方法的一个载体，通过解题的过程，理解知识的原理，提炼方法的本质，注重解法的策略，让学生解题有“一题多解”的能力，也有“多解归一”的认识，这才是解题教学的目标.